诱导轮非对称空化流动数值计算和试验研究

李龙贤，温永鑫

（1.北京航天动力研究所；北京 100076；2.北京电子工程总体研究所；北京 100854）

0 引言

在航天推进系统中，对作为中大推力液体火箭发动机关键增压装置的涡轮泵的工作稳定性和可靠性等有严格的要求。诱导轮作为涡轮泵的前置增压部件，对改善涡轮泵的抽吸性能、降低推进剂贮箱内部压力及质量具有重要作用。高性能诱导轮转速较高，通常允许流场内存在一定程度的空化，但空化的产生会使流场趋于不稳定，甚至对发动机的工作稳定性和可靠性产生影响。

诱导轮内的空化存在多种形式，非对称空化是已知的一种存在于涡轮泵扬程下降过程中的复杂流动现象。对于附着型非对称空化，诱导轮内各通道的空化区长度表现出明显的不同。在此工况下，须单独考虑和分析每个叶片，但这将使得空化模型变得非常复杂。Horiguchi等[1]利用奇点方法给出了预测交替型空化的近似模型，为非对称型空化的预测提供了重要的借鉴。本文基于奇点法理论，并结合空化波动理论对某低温介质三叶片诱导轮的非对称空化特征进行研究。

1 研究方法

1.1 研究对象

以某低温介质三叶片变螺距诱导轮为研究对象。为了计算及试验方便，将离心轮、扩压器、诱导轮等组成涡轮泵整体，模型如图1所示，诱导轮实物如图2所示。诱导轮的实际工作介质为低温液氧，但在本文研究中由于采用低温介质进行试验难度和风险较大，故采用密度和黏度相近的常温水代替。

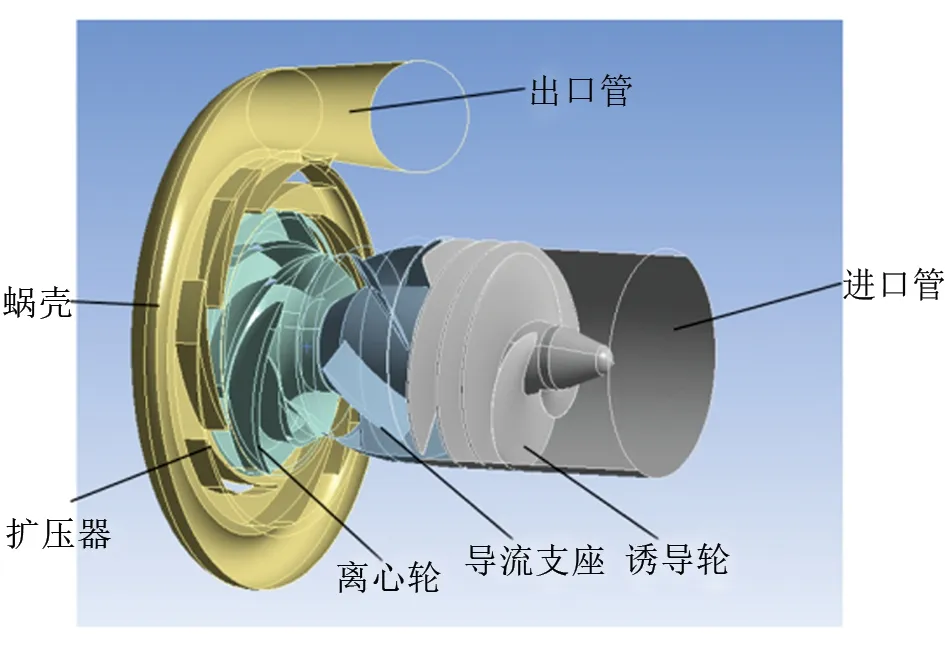
图1 液氧涡轮泵几何模型Fig.1 Liquid oxygen turbopump geometry model

图2 诱导轮实物图Fig.2 Physical view of inducer of liquid oxygen turbopump

1.2 控制方程

控制方程主要由连续方程、动量方程、能量方程构成。其中连续方程为混合相质量守恒方程，在连续方程中增加一个气态相或液态相质量守恒方程并带入质量输运源相，便可导入空化模型[2]。

（1）连续方程

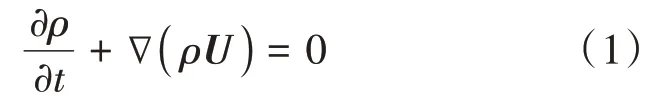
式中：t为时间；ρ为气液两相流体密度，ρ=αlρl+αvρv；U为速度向量；∇(ρU)为速度散度。αl为液体体积分数；ρl为液体密度；αv为气体体积分数；ρv为气体密度。

（2）动量方程

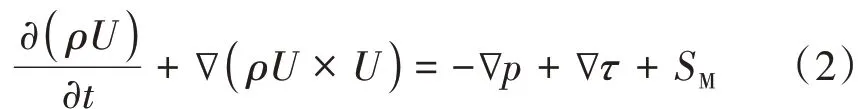
式中：U×U为向量积；τ为表面力，∇τ为表面力τ的散度；p为流场压力；SM为由体积力牵引的动量源项。

（3）能量方程

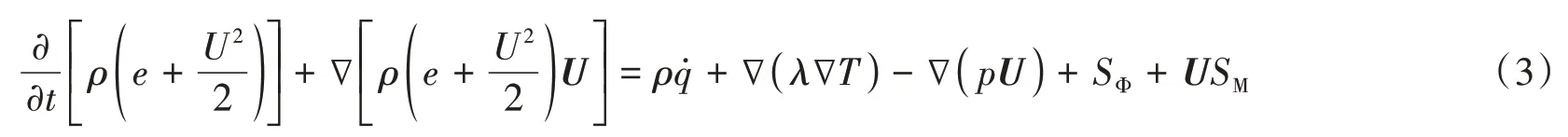
式中：e为工质内能；U为速度标量值；T为工质温度；q̇为工质与外界的热交换量；SΦ为耗散函数。

（4）空化模型及空泡动力学方程

空化模型为基于均质多相质量输运模型的空化模型（又称1方程模型），并假设相间无滑移。数值计算过程中，包含多相流及空化的计算模型适用于常规的黏性流体力学计算方法，常规计算单相流的湍流模型对于多相流流场计算依然适用[3]。

式中：Re、Rc分别表示气泡产生和气泡溃灭的质量输运源项。

空泡动力学方程采用Rayleigh-Plesset方程[4]，即：

式中：RB为空泡半径；pv为饱和压力；p∞为远场压力；S为液体表面张力系数；νl为液体运动黏度。

采用上述组合模型计算出的结果能较好地反映出空化区随流场压力的变化情况。基于Rayleigh-Plesset空泡动力学理论推导出的空化模型为均匀化模型，目前很难用质量输运空化模型准确预测附着型非对称流动[5]流场内空化区波动以及不对称特性。因此，本文引入奇点法表示空化波动方程，即：

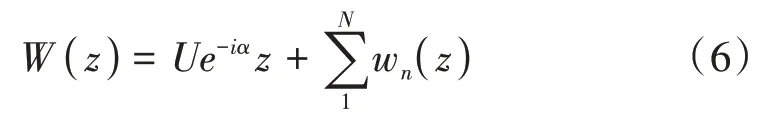
式中：Ue-iαz表示主流流动势；N表示叶片数；wn为流场受第n个叶片的扰动，其物理意义是受源项及叶片上漩涡影响的流动势，单位为J/g。

采用空化数σ定量描述空化的剧烈程度[6]，空化数为无量纲参数，其数学表达式为：

式中：p∞和u∞分别为液体流动参考压力和参考速度，在叶轮机械流场中，p∞通常取入口总压pin；u∞取叶尖圆周速度uT，因此空化数可以表示为[7]：

式中：Ω为角速度；rT为叶片圆周半径。若不计比尺效应，理论上如果空化数σ相同，空化程度也相同[8]。

1.3 试验研究

图3为诱导轮空化试验及测试系统示意图。系统主要由三个分系统组成：泵组合体外特性参数试验系统、流场脉动压力测量系统和空化流场可视化试验系统。由于直接用低温工质进行试验的难度大，成本较高，试验风险较大，因此，采用与实际低温工质液态氧黏度和密度等物性参数相近的常温水进行试验。

图3 诱导轮空化试验及测试系统Fig.3 Diagram of inducer cavitation test system

图4为试验系统现场图。试验过程中采用高速相机通过观察窗口连续高速拍摄流场的瞬态图像。

图4 可视化试验系统现场图Fig.4 Visualization test system

诱导轮空化流场观测窗口采用透明有机玻璃制成，图5为观测窗口实物图。

图5 诱导轮空化观测窗口实物图Fig.5 Inducer cavitation observation window

2 数值计算和试验结果分析

2.1 数值计算结果分析

图6为试验和数值仿真计算结果的对比。

图6 空化数-泵出口压力系数曲线Fig.6 Cavitation number-pump outlet pressure coefficient curve

由图6可以看出，由数值计算得出的泵出口压力系数ψ随空化数σ的变化关系曲线与试验结果吻合较好，说明由数值计算得出的泵组合体外特性参数比较准确，最大误差在5%以内。压力系数：

式中：pout为泵出口压力，压力系数和空化数均为无量纲参数。

通过数值计算和试验可以发现，本文研究的诱导轮，非对称空化区开始出现的空化数σ≈0.03，空化数区间为0.01≤σ≤0.03，非对称空化出现的空化数与断裂扬程发生时空化数很接近（断裂扬程指泵出口压力系数急剧下降阶段所对应的泵扬程）。

以空化数σ=0.022为例，介绍试验过程中观测到的非对称空化区的特征。图7为σ=0.022情况下诱导轮叶片和导叶叶片表面动态压力分布云图。可以看到，此时低压区已覆盖叶片前缘部分，压力最低的区域分布在吸力面修圆的表面和叶尖处。

图7 叶片表面压力动态分布试验云图Fig.7 Test image of pressure dynamic distribution on blade surface

图8为σ=0.022工况下诱导轮叶片通道内空化区随时间变化的动态云图，（a）中的0°（0 s）为初始角度（初始时刻）流场试验云图，（b）（c）（d）依次为诱导轮转过90°、180°、270°时在同一观测位置观察到的诱导轮叶片流场云图。可以看出，此时空化区主要分布在叶片前缘附近吸力面表面及叶片修圆吸力面上，叶片通道间的空化区表现出明显的非对称性，同时每个叶片上的附着空化区也在不断地伸缩变化。

图8 叶片通道内空化区动态分布试验云图Fig.8 Cavitation area dynamic distribution on stator and rotor blade surface

图9为采用数值计算得到的叶片通道内空化区 的动态分布图。除了附着在叶片修圆段外缘以外的空化区，靠近叶根的空化区以云状气团的形式 分布在叶片通道入口，对通道造成阻塞。

图9 叶片通道内非对称空化区数值计算云图Fig.9 Nonsymmetrical cavitation area in flow passge obtained by numerical simulation

非对称空化出现时伴随着大量的空化区气泡的脱落和破碎，按照空化的类别，此时的空化属于片空化和云空化的混合态[9]。云空化是由片空化发展到一定程度气泡在下游脱落破碎产生的，是由大量微泡群和液态工质混合而成的两相流。云空化的形成与片空化的尾部回射流以及片空化的整体失稳密切相关。云空化的出现总是与流动失稳、旋涡和湍流脉动等复杂流动现象联系在一起，其发生、发展和溃灭会带来结构的震动、噪声和空蚀[10]。此时泵在外特性上表现为扬程降低3%，工程上认为泵内开始发生空蚀。云空化的出现从微观的角度解释了空蚀出现的原因。

图10为空化数σ=0.022时计算得到的诱导轮叶片修圆末端横截面上的压力动态分布。可以看出，此时截面大部分被低压区覆盖，压力较高的区域只出现在叶片压力面叶尖处及叶片表面小部分区域，压力的等压线随时间变化非常明显。

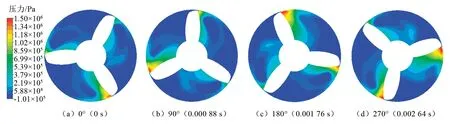
图10 叶片修圆末端横截面压力动态分布数值计算云图Fig.10 Pressure dynamic distribution on blade tip relief cross section by numerical calculation

图11为σ=0.022时计算得到的该截面空化区随时间的动态分布。可以看到，空化区主要分布在吸力面叶尖及叶中表面上。从图11可以清晰地看到空化区在三个叶片的非对称性分布。为便于分析，将诱导轮叶片编号，圆心处的箭头方向为诱导轮旋转方向，附着空化区面积最大的为叶片1，沿着与诱导轮旋转方向相反的方向依次为叶片2和叶片3；叶片1、2、3下游的叶片通道分别为通道1、通道2和通道3。叶片1表面的空化区体积分数明显高于叶片2和叶片3表面；从图11可以较明显地看到空化区气泡脱落过程。空化区气泡脱落发生在叶片吸力面，部分空化区气泡脱落并逐渐消失（图11红色虚线圈内为空化区变化过程）。空化区气泡脱落是云空化形成的诱导因素。

图11 叶片修圆末端横截面空化区动态分布数值计算云图Fig.11 Cavitation area dynamic distribution on blade tip relief cross section by numerical calculation

图12为空化数σ=0.022时诱导轮三个叶片表面平均空化区体积分数。可以看到，此时叶片上的空化区以大致相同的周期随时间不断波动，空化区波动周期约为叶轮旋转周期的3倍；叶片3表面的空化体积分数平均值比叶片2高出约25%，三个叶片上的空化区呈现出明显的非对称性。

图12 诱导轮叶片表面空化区体积分数波动曲线Fig.12 Fluctuation curve of inducer blade surface cavitation area volume fraction（σ=0.022）

2.2 试验结果分析

图13～15分别为诱导轮3个叶片依次经过观察窗口的连续成像，试验工况为转速4 000 r/min，空化数σ=0.022，流量系数φ=0.059，在此阶段发现了比较强烈的非对称空化，通道1的空化区比其他两个要剧烈得多。Tsuijimoto[9]也在试验中发现了这种非对称空化，并证实这种空化不稳定形式出现的空化数要小于旋转空化。这种形式的非对称流动流道中的空化区较稳定，空化区随叶片旋转而同步旋转，这与旋转空化截然不同，将这种非对称空化称之为附着型非对称空化。这种流道中的非对称空化区为云空化的一种，诱导轮中云空化的出现是扬程开始显著下降和叶片空化破坏的诱导因素，云空化出现时对应的空化数与断裂扬程对应的空化数非常接近。

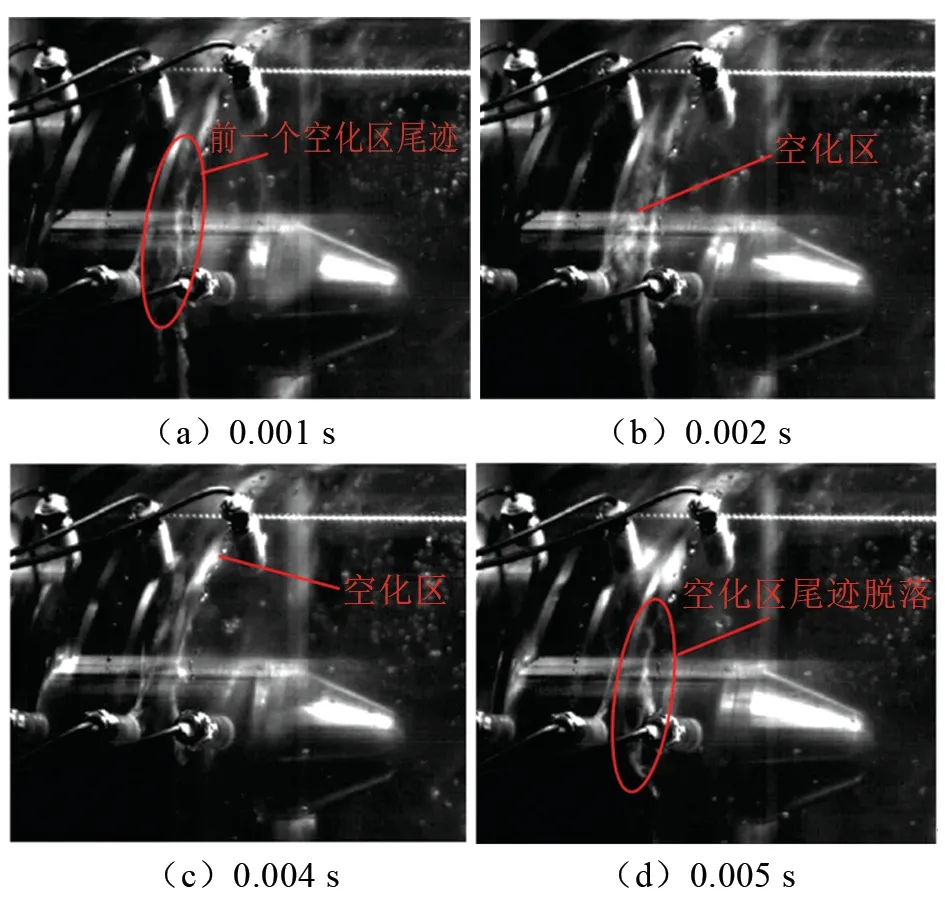
图13 通道1空化区连续成像Fig.13 Continuous imaging for the first blade channel cavitation area

图16为从试验结果中提取的空化区光学图像，从该组图像中可以更清楚地看到诱导轮3个叶片通道中的空化区差异。

图14 通道2空化区连续成像Fig.14 Continuous imaging for the second blade channel cavitation area

图16 空化区光学图像Fig.16 Cavitatoin area optical image

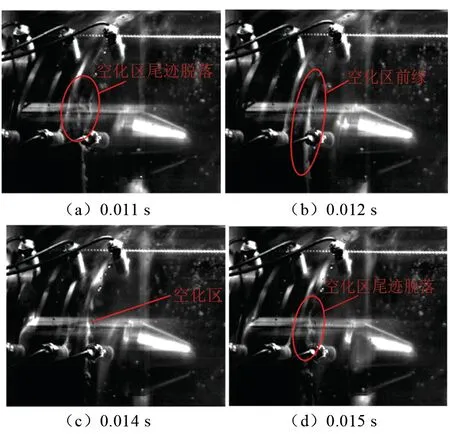
图15 通道3空化区连续成像Fig.15 Continuous imaging for the third blade channel cavitation area

图17为经过图像处理后得到的空化区等高线图像。

图17 不同通道的空化区等高线图像Fig.17 Cavitation area contour line image

对图17的图像进行光谱亮度分析，得到空化区频谱能量概率统计图，如图18所示，这是对空化图像特征的定量分析[11]。可以看到，通道1的频谱能量峰值均明显大于其他两个通道，表明通道1内的空泡数量、空泡密度均大于另外两个通道，通道2和通道3内的空化区分布规律比较接近。

图18 频谱能量概率统计Fig.18 Spectrum energy probability statistics

利用图像的灰度直方图提取诸如均值、方差、能量及熵等来描述图像特征[13]。设（x，y）为图像中的一点，该点和离它只有微小距离的点（x+Δx，y+Δy）的灰度差值gΔ为：

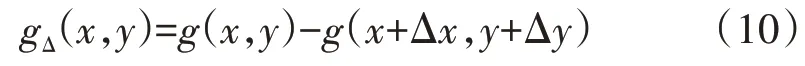
式中：设灰度差值的所有可能取值有m级，点（x，y）在整个图像上移动，统计出gΔ取各个数值的次数，由此做出gΔ的直方图。由直方图可以得到gΔ取值的概率p（i），p（i）表示第i级灰度出现的概率，相关的特征参数有[14]：灰度平均值灰度对比度，其中灰度平均值表示图像的亮度，平均值越大，图像平均亮度越亮，图像中的空泡越多。对比度表示图像的亮度差值，对比度越大，图像中的空泡越密集，熵表示图像的平整程度，熵越大，空化区分布越均匀。

对表1空化区图像特征参数进行分析，可以看到，通道1的灰度平均值、对比度及熵均明显大于其他两个通道的空化区，表明通道1内的空泡数量、空泡密度均大于另外两个通道。通道2和通道3内的空化区分布规律非常接近。

表1 空化图像特征分析（σ=0.022）Tab.1 Characteristic analysis for cavitation image（σ=0.022）

图19为经过平均化处理的不同叶片背面上的附着空化区长度及不同通道的流量随空化数的变化关系。

图19 通道空化区长度及流量的归一化处理Fig.19 Averaging treatment for cavitation area length and flux in different channel

图19曲线上标注的数字对应叶片编号，lc表示空化区长度，lm表示空化混合区长度，Q表示叶片流道内流量。可以看到，叶片上出现不对称附着空化区的空化数范围为0.02≤σ≤0.035，非对称空化出现时通道内的流量也随之不对称，空化最严重的通道1流量最小，旋转阻塞只是出现在空化程度最严重的通道1中[5]。随着空化数继续降低，空化区的不对称性也逐渐降低，当空化数进一步降低，诱导轮扬程接近断裂扬程，此时空化区已蔓延至叶片后缘，通道内的空化区不对称性消失。

3 结论

诱导轮内的空化存在多种形式，非对称空化是已知的存在于涡轮泵扬程下降过程中的复杂流动现象的一种。本文采用数值计算和试验方法对某低温介质诱导轮流场中的非对称空化进行了研究，得出以下结论：

（1）数值计算和可视化试验证明了非对称空化的存在，数值计算结果与可视化试验结果一致性较好，说明本文中所采用的奇点法空化波动方程数值计算方法预测的非对称空化具有较好的准确性；

（2）扬程明显下降时叶片通道出现明显的非对称性，对应诱导轮的空化数为σ=0.03；

（3）三叶片诱导轮内发生非对称空化时，其中一个通道内的空化区明显大于其他两个通道，且每个通道的空化区大小以一个特定值为中心随时间成周期性波动；

（4）非对称空化出现后，通道内的流量也随之变得不对称，空化最严重的通道对应的流量最小。旋转阻塞只是出现在空化程度最严重的通道中；

（5）非对称空化的出现只发生在特定空化区域，对于本文研究的诱导轮0.02≤σ≤0.035。空化数进一步降低，诱导轮扬程接近断裂扬程，此时空化区已蔓延至叶片后缘，叶片通道内的空化区不对称性消失。