基于“教育目标分类学”原理的目标、教学、测评整体设计
谢俊峰
(江苏省扬州市朱自清中学)
一、前言
“布卢姆教育目标分类学”原理将知识分为四个类别,认知过程分为六个层次,并将四类知识和六个层次的认知过程放入二维表格中,形成了教育目标分类框架表. 利用这一原理可以增进教师对教学目标的理解,借助教育目标分类框架表可以进行目标、教学、测评的整体设计,并分析三者的一致性程度,从而提高教学效果,提高教学质量.
江苏省扬州市初中数学乡村骨干教师培育站关注教学目标制订,开展了基于“布卢姆教育目标分类学”原理的目标、教学、测评的整体设计研究,针对具体的教学课程,导师与学员组织了多次研讨. 下面结合苏科版《义务教育教科书·数学》(以下统称“教材”)八年级上册“勾股定理”章节的“勾股定理的简单应用”这节研讨课来进行简单论述.
二、基于原理的目标、教学、测评整体设计
1. 教学目标设计
教学目标在整个教学流程中占据主导地位,目标设计的准确性与合理性将直接影响课堂教学的成效.“布卢姆教育目标分类学”教育目标的呈现以“动词+名词”形式,其中动词通常描述预期的认知过程,名词描述期望学生习得或建构的知识. 利用布卢姆教育目标分类学的表述方法,可以使得目标的呈现更加清晰、表达更加准确,让教师对于课堂“教什么”“教到什么程度”更加清楚.
(1)初设教学目标.
本次上课的教师,结合《义务教育数学课程标准(2011年版)》及教材,利用原理列出了本节课的如下教学目标.
目标1:回顾勾股定理及其逆定理的内容.
目标2:辨析勾股定理及其逆定理在实际应用中的联系与区别.
目标3:应用勾股定理及其逆定理解决生活中的简单问题.
目标4:在解决实际问题的过程中,体会将解斜三角形的问题转化为解直角三角形的问题的过程,感悟数学的转化思想.
目标5:在将生活问题抽象为几何图形的过程中,逐步发展学生的数学抽象、数学建模思想,使他们体会勾股定理的文化价值,增强应用意识.
(2)共研教学目标.
导师组在分析教学目标后,与授课教师进行了交流,对目标提出了两点修改建议.
①本节课是勾股定理的简单应用,回忆勾股定理及其逆定理可以在教学过程中体现,作为本节课的目标之一则不适合,因此目标1可以从本节课的目标中去除.
②目标2 表述上不太恰当,定位为分析层次明显要求太高,学生仅需要理解、比较两者的不同,并在实际应用中能够正确选择定理即可.
(3)重设教学目标.
授课教师结合导师的分析及建议,重新设计了本节课的教学目标.
目标1:比较勾股定理及其逆定理之间的关系,能在实际应用中正确选择两种定理.
目标2:运用勾股定理及其逆定理解决生活中的简单问题.
目标3:在解决实际问题的过程中,体会将解斜三角形的问题转化为解直角三角形的问题的过程,感悟数学的转化思想.
目标4:在将生活问题抽象为几何图形的过程中,逐步发展学生的数学抽象、数学建模思想,使他们体会勾股定理的文化价值,增强应用意识.
将这4个目标放置在如表1所示的分类表中,上述4 个目标对应原理的认知维度与知识维度分别为:目标1:理解概念性知识(B2);目标2:执行程序性知识(C3);目标3:实施程序性知识(C3);目标4:生成元认知知识(D6).
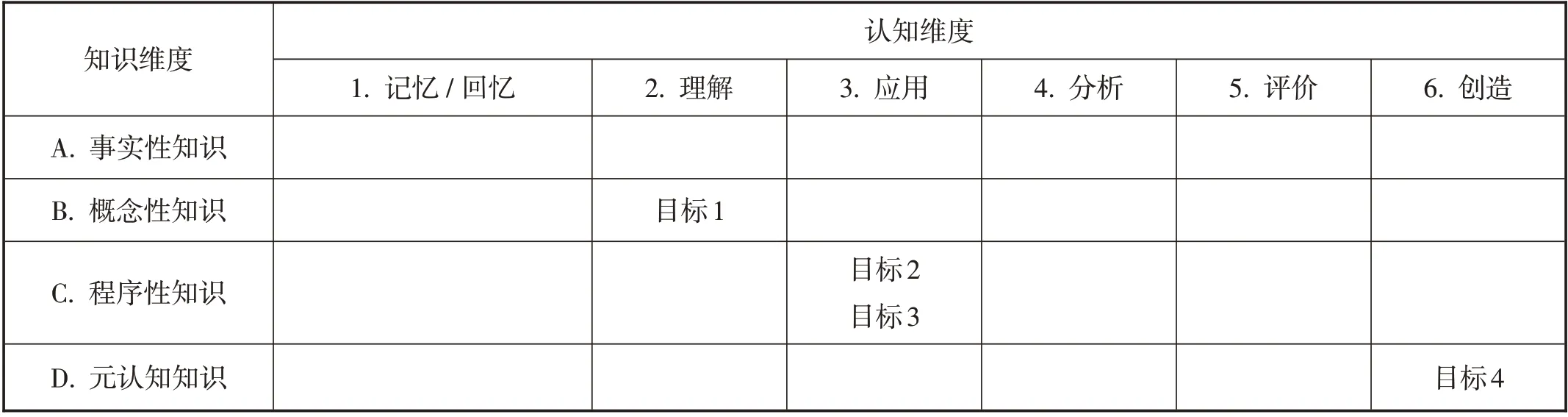
表1 目标在分类表中的位置
【说明】目标2 和目标3 中“执行”与“实施”都是“应用”认知维度的两个类别,但它们还是有区别的. 执行是指当学生在遇到熟悉的任务时机械化地执行一个程序,如有理数的计算、解一元一次方程、解分式方程等. 实施是指学生选择和使用一个程序去完成不熟悉的任务,需要学生根据已有知识确定解决问题需要的程序,再使用选择的程序来解决问题,如证明两条线段相等、解一元二次方程等. 同时,勾股定理及其逆定理在知识类别中属于概念性知识,但本节课的教学目标是定理的简单应用,我们关注的不应是作为概念性知识的“定理”,而应是运用定理解答问题的程序,即程序性知识,目标2、目标3应该被归入到方格C3,而不是方格B3.
2. 教学过程设计
(1)教学初设计.
授课教师初步设计了课堂教学流程,并进行了说课,教学过程简述如下.
活动1:知识回顾.
前面我们学习了勾股定理及其逆定理,同学们回忆一下勾股定理的内容.
活动2:情境引入.
例1 在现实生活中,我们经常会看到一种不文明的现象,如图1,在一块长方形花圃中,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”. 如图2,若沿着拐角的两边走,要分别走6米和8米,大家计算走“捷径”少走了_____步,但却踩伤了花草.(假设1米为2步.)

图1
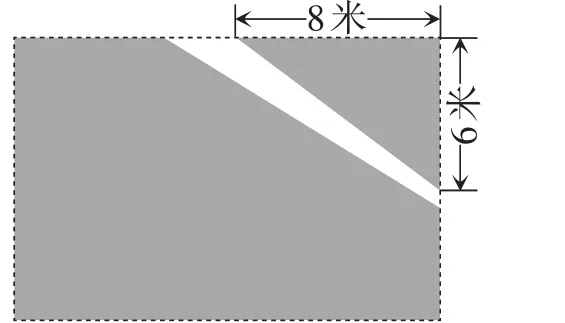
图2
教学过程略,解题后总结如图3所示.
活动3:实际应用.
例2 如图4,《九章算术》中的“折竹”问题:今有竹高一丈,末折抵地,去根三尺,问折者高几何?题意是:有一根竹子原来高度是1 丈(1 丈=10 尺),竹子被折断,竹子顶端触地面处距离竹根有3 尺,试问竹子折断处离地面的高度.

图4
教学过程略,解题后总结如图5所示.

图5
活动4:例题探究.
例3 如图6,在△ABC中,AB= 26,BC= 20,BC边上的中线AD=24,求AC.

图6
教学过程略,解题后总结如图7所示.

图7
活动5:操作探究.
例4 如图8,现有一个圆柱,若小明在吃东西时留下了一点食物在点C处,恰好一只在点A处的蚂蚁捕捉到这一信息,于是它想从点A处爬到点C处,你们想一想,蚂蚁可以怎么爬?怎样爬较近?若已知圆柱高为12,底面半径为3,π取3.

图8
教学过程略,解题后总结如图9所示.

图9
活动6:课堂小结.
①利用勾股定理及其逆定理求直角三角形未知边,以及周长、面积等.
②将生活中的实际问题转化为数学问题,利用勾股定理及其逆定理求解.
③将非直角三角形问题转化为直角三角形问题求解,体会转化的数学思想方法.
④将立体图形中的路径问题转化为平面图形问题,再利用勾股定理及其逆定理解决实际问题.
(2)研讨与改进.
导师在听完授课教师的说课后,围绕教学目标,就教学设计中存在的问题进行了研讨,并提出了改进的建议.
①教学活动1 的设计是让学生回顾勾股定理及其逆定理的内容,这样的设计略显枯燥,可以围绕目标,改为小题练习.
修改设计如下:
a. 一个直角三角形的两直角边分别为3 和4,则三角形的周长为 ,斜边上的高为 .
b. 一个三角形三边分别是6 cm,8 cm,10 cm,这个三角形的面积为 .
问题的设计让学生在练习的过程中复习回顾了勾股定理及其逆定理,同时求三角形未知边长、高、周长及面积等也是定理应用的体现,与教学目标的贴合度更高.
②教学活动5 的设计是应用勾股定理解决实际问题,但其中涉及的知识点较多,从教学过程来看,它需要学生回忆并理解圆柱的侧面展开图,计算不同爬行路径的长度,还要学生判定爬行距离最短,涉及的认知过程有回忆、理解、应用、分析等,其中虽然涉及勾股定理的应用及数学转化的思想,但在此题中不是重点,与教学目标不符.
修改设计如下:
a. 如图10,王老伯有两块三角形地块,通过测量的数据,你能帮忙求出两块地的面积吗?
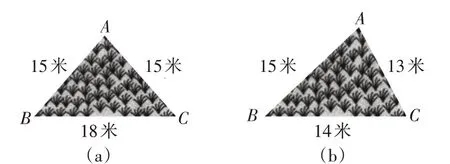
图10
b. 王老伯还有一块四边形菜地,如图11所示,试帮王老伯再计算一下这块菜地的面积.

图11
其中问题a 需要学生添加适当的辅助线,将非直角三角形转化为直角三角形,再利用勾股定理进行计算. 问题b 需要学生添加辅助线,将四边形转化为三角形,在计算中既有勾股定理的应用,也有勾股定理逆定理的应用,与本节课的教学目标贴合度较高.
③教学活动6 是总结环节,与研讨2 类似,把“将立体图形中的路径问题转化为平面图形问题,再利用勾股定理及其逆定理解决实际问题”作为本节课的知识点进行总结,与本节课的教学目标有一定偏离.同时,授课教师把本节课知识点列在课件上带领学生回顾总结,这样的总结实质效果不大.
修改设计如下:
a. 本节课我们学习的主要内容是什么?
b. 本节课学习中运用了哪些数学思想方法?
c. 勾股定理及其逆定理在实际生活中还有哪些应用?试举例说明.
通过问题引导学生进行思考与总结,构建知识体系,突出了学生的主体性,问题c 具有开放性,促进学生进一步思考定理的实际应用.
将修改后的教学活动放置到分类表中,如表2所示.
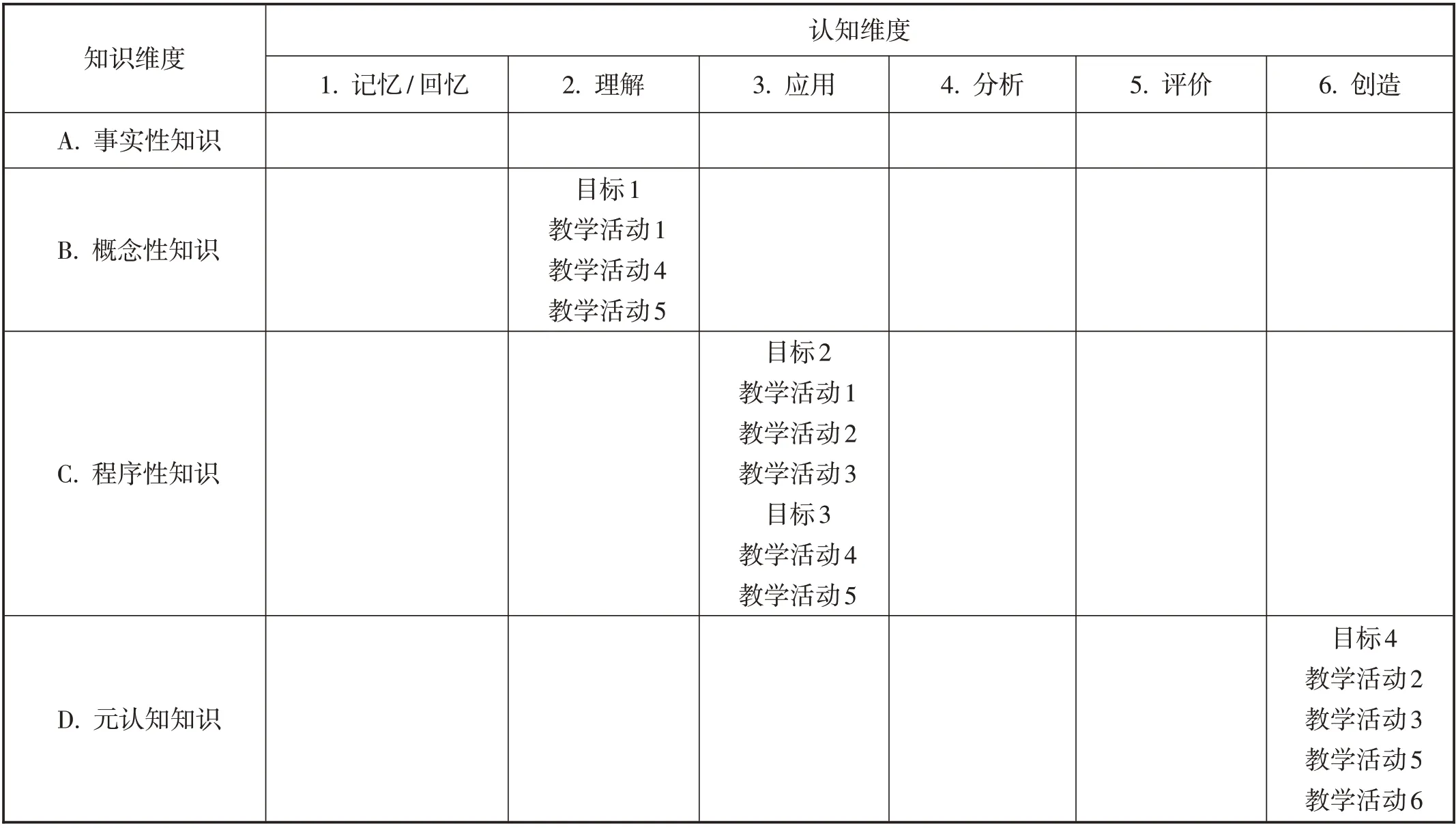
表2 目标、教学活动在分类表中的位置
【说明】教学目标达成渗透在各个教学过程中,因此在表格中教学活动2、教学活动3对应的教学目标不仅是教学目标2,也对应着教学目标4,教学活动4、教学活动5对应着教学目标1和教学目标3. 教学目标4是生成元认知知识,这个目标的达成也是在多个教学活动中逐步实现的.
3. 教学测评设计
测评是检验教学成效的有效手段. 为检测教学效果,授课教师结合教学目标编制了本节课的测试题.导师将试题放置到分类表中,每道试题都对应着相应的教学目标,没有超出目标的要求,导师肯定了授课教师的设计.
测试题目设计如下:
①一根电线杆在距离地面8 m 处断折,电线杆顶部落在离电线杆底部15 m 处,电线杆折断之前长度为_________.②若直角三角形的一条直角边长是9 cm,斜边比另一条直角边长1 cm,求该直角三角形另一直角边长度为_________.
③如图12,在锐角三角形ABC中,AD⊥BC,AD=12,AC=13,BC=14.求AB的长.

图12
④如图13,已知在△ACD中,AB=13,AC=12,BC=5,AD=20,求BD的长.

图13
⑤《九章算术》中的“引葭赴岸”问题:今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何?题意是:如图14,有一个正方形池塘,它的边长为10尺,在池塘的中央一根芦苇AB,其中高出水面部分CB为1 尺,把该芦苇顶端B拉至与水面齐平的点B′处,问池塘的水深和这根芦苇长各多少尺.目标、测评放到分类表中,如表3所示.

图14

表3 目标和测评在分类表中的位置
4. 实践与分析
目标、教学、测评是教育教学中需要重点关注的三个方面,它们是相互交替、相互影响的整体,我们不能孤立地看待三者的存在,要重点关注三者之间存在的关系,以及关系的交替、融合和匹配的程度. 借助布卢姆教育目标分类表我们可以进行目标、教学、测评整体设计,其中包含目标、教学、测评的方格,说明三者具有高度的一致性,反之则一致性偏弱. 本节课经过导师与学员的研讨与改进后,通过表2与表3,可以看出本节课三者之间的一致性程度高. 授课教师根据教学设计开设了研讨课,课后进行了测评. 从现场教学来看,授课教师教学活动实施有序,条理清晰,教学目标在教学活动中得以实现. 从测评结果来看,大部分学生均已掌握了本节课的相关知识与方法,教学目标达成度高,但测评中也反映了教学过程中的一些细节问题,分析如下.
全班共有50人,测评结果如表4所示.

表4 学生测评结果分析
总体看学生出现的主要错误:一是审题不清导致的错误,如测试题目①、测试题目②,测试题目①错误答案为17,均为结果没有加上8,测试题目②错误答案为41,是将直角边与斜边混淆;二是计算的错误,如测试题目③、测试题目④、测试题目⑤. 从测评结果来反思教学行为,我们发现授课教师授课时,在读题环节用时较少,题目一读而过,很快就进入讲题环节,学生对题目不理解,导致了在测评中出现了诸多低级错误. 测试题目⑤与教学活动3 的例题有相似之处,有8 人是空白或乱写. 在课堂教学的过程中,授课教师在把实际问题抽象为数学问题的过程中以讲授为主,缺少学生自主建构的过程,部分学生在独立面对同类型题目时,就出现了问题. 因此,在课后,导师提醒授课教师要注重审题,重视问题分析的过程,做好示范与板书等细节,要发挥学生的主动性,突出学生的主体地位,促进学生的深度学习,发展学生的高阶思维能力.
三、基于原理的目标、教学、测评整体设计思考
关于目标、教学、测评整体设计的相关研究起源于对教育质量的高要求,其落脚点是学生. 美国教育心理学家科恩在研究中发现,在目标、教学、测评一致性较高的课堂,无论是普通学生还是优等生都能取得很好的学习效果. 崔允漷教授在研究中也发现,在课程实践中,如果目标、教学、测评一致性程度越高,那么可以较有把握地预测学生在阶段性的学业评价考试中获得更好的成绩,同时会提升学生的学习幸福感、自我效能感和学习兴趣. 因此,教师要重视目标、教学、测评的整体设计,在提升自身教育教学能力的同时,也能够有效促进学生的进步,提升学生的素养.
目标、教学、测评这三者中,教学目标的定位是基础,它明确了学生学习的具体任务,即使教学活动有了清晰的方向,又使教学测评有了显性的标准,教学目标的明确是教学质量的保证,它是教学活动的出发点和归宿,没有清晰的目标就谈不上教、学、评的专业实践,没有清晰的目标,更谈不上一致性. 因此,在教学中要将教学目标的制订放在首要位置. 若教学与目标不一致,那所有的教学活动都是徒劳的,甚至会出现反作用;若测评与目标不一致,评估的结果就无法反映目标是否达成或者达成的程度;当然如果教学与测评不一致,再高质量的教学也无法在评估中得到检测,教师也无法根据评估去指导教学进程.
利用分类表进行目标、教学、测评整体设计,对一线教师进行专业的教学设计有相当强的指导作用.如果教师在进行教学设计时,都能够把教学目标、教学活动和测评问题放到相应的表格中,借助分类表进行分析,就可以了解教与学的效果. 同时可以借助分类表反思教学. 例如,教学目标是否达成,教学成效是否显著,教学过程是否还可以进行改进,等等. 这样教师的教学就不仅仅会停留在单一的理论或者是经验的层次,而是在理论指导下的教学实践与研究.

