基于数学抽象素养培养的初中函数概念教学

杨小丽，张雅丽

（北京教育学院数学系；北京市通州区牛堡屯学校）

数学抽象素养是《普通高中数学课程标准（2017年版）》提出的数学学科六大核心素养之一. 数学抽象是指通过对数量关系与空间形式的抽象得到数学研究对象的素养. 数学抽象的一个重要表现是数学概念的形成. 因此，概念教学是发展学生数学抽象素养的重要载体. 下面以初中函数概念为例，探讨如何在概念教学中发展学生的数学抽象素养.

一、函数概念教学的典型设计

函数概念的典型设计如下. 首先，给出一组现实情境，接下来教师提问：同一个问题中的变量有什么联系？师生交流后，教师对每一个情境做出如下分析：x和y是两个变量，每当x确定一个值时，y就有唯一确定的值与其对应.然后，归纳：上面每个问题中的两个变量相互联系，当其中一个变量取定一个值时，另一个变量就有唯一确定的值与其对应.最后，给出函数的定义：一般地，在一个变化过程中，如果有两个变量x和y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数.

学习函数概念的难点是要抽象概括出“对于x的每一个确定的值，y都有唯一确定的值与其对应”这样一个结论. 从上述教学设计可以看出，该结论是由教师直接分析给出的，并没有真正突破函数概念学习的难点.

二、课前调研及结果分析

在学习函数概念之前，为了了解学生的抽象概括水平，笔者对所任教班级24名学生做了调研.

1. 前测题

（1）从下面的问题情境中，你获取了哪些信息？写出你所发现的信息.

情境1：图1是某地一天内温度的变化情况. 写出你所发现的信息.

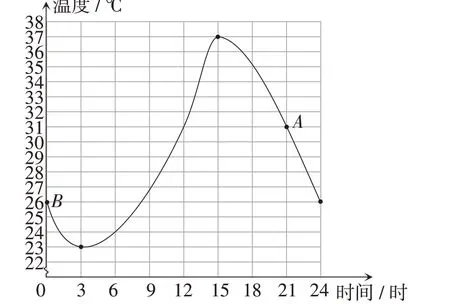
图1

情境2：在高海拔（1 500～ 3 500 m 为高海拔，3 500～ 5 500 m 为超高海拔，5 500 m 以上为极高海拔）地区的人有缺氧的感觉，表1 是有关海拔高度与空气含氧量之间的一组数据. 写出你所发现的信息.

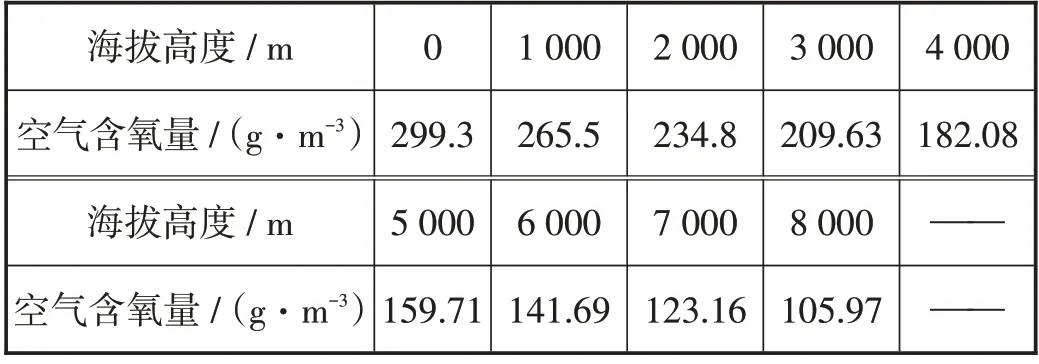
表1 海拔高度与空气含氧量数据

情境3：每张电影票的售价为50 元，设一场电影售出x张票，票房收入为y元. 写出你所发现的信息.

（2）上述几个具体情境的共同点是什么？

2. 前测结果

对于第（1）小题情境1，学生答题情况如表2所示.

表2 情境1的答题情况

对于第（1）小题情境2，学生答题情况如表3所示.

表3 情境2的答题情况

对于第（1）小题情境3，学生答题情况如表4所示.

表4 情境3的答题情况

对于第（2）小题，学生答题情况如表5所示.

表5 第（2）小题的答题情况

3. 前测结果分析

从上述前测结果可以发现，第（1）小题中，对于情境1，83.3%的学生能够观察得到温度随时间的变化而变化；对于情境2，87.5%的学生能够得到随着海拔的升高空气中的含氧量在降低；而对于情境3，只有37.5%的学生能够说出“电影票售出张数越多，票房收入越多；每多售出1 张电影票，票房收入就增加50 元”，但有91.7%的学生能够写出函数解析式.

第（2）小题让学生归纳几个具体情境的共同特点，有50%的学生能够指出：都是一个变量随着另一个变量的改变而改变. 没有任何1名学生能够说出“对于x的每一个确定的值，y都有唯一确定的值与其对应”这样的结论. 说明学生很难抽象概括出教材中的函数定义. 那么，教学中如何突破该难点，并让学生深入理解教材中的函数定义呢？

三、教学过程设计与实施

在实际教学中，笔者尝试了3 个课时的小单元教学设计. 由于篇幅所限，仅呈现几个主要环节的教学片断.

环节1：回顾前测问题.

教师出示前测中的3个情境.

问题2：变量之间有关系吗？如果有，它们之间有什么关系？

问题3：上述几个具体情境的共同点是什么？

【设计意图】3个情境分别以图象、表格、表达式三种形式呈现，以让学生感受函数表达的多样性，同时为后面学习函数的表示方法奠定基础. 通过问题1，引出常量和变量的概念；通过问题2和问题3，让学生经历观察、比较、分析、归纳等活动，抽象概括出3 个情境的共同属性：都是一个变量随着另一个变量的变化而变化.

环节2：观察共性，抽象概括.

教师出示另一组情境.

观察两组患者临床治疗效果，并将其划分为以下4个指标：（1）痊愈：患者在治疗后，所有临床症状均消失，并且没有出现复发情况；（2）显效：患者治疗后临床症状基本消失，白带清洁度也有所提高；（3）有效：患者治疗后取得了较明显的治疗效果，白带清洁度有所提高；（4）无效：患者治疗后没有取得任何效果，甚至出现病情恶化的情况[2]。

情境4：小红一天中的体温变化情况如图2所示.

图2

情境5：某话费套餐收费标准如表6所示.

表6 某话费套餐收费标准

情境6：某地出租车5：00—23：00 收费标准如下：3公里以内收费13元；超出（含）3公里的部分每公里2.3 元；燃油附加费1 元/次. 设车费为y元，行驶里程为x公里.

问题4：上述情境中有哪些量？分别是什么？哪些是变量？

问题5：变量之间有什么关系？

生1：情境4中，体温随着时间的变化而变化.

生2：情境4中，12时至17时，体温没有变化.

追问1：如何描述图2 中从12 时至17 时这段时间的图象中两个变量之间的关系呢？

生3：给出时间的一个量就能找到一个对应的体温值. 12时对应的体温是37℃，12时至17时对应的体温都是37℃.

追问2：再加上其他部分呢？两个变量之间的关系如何描述？

生4：给出一个量的固定值，就能找到另一个量的固定值.

问题6：这组情境与第一组情境变量之间的关系有区别吗？如果有，是什么？

生5：有区别，第一组情境中变量之间的关系都是一个变量随着另一个变量的变化而变化；第二组情境中存在某一段一个变量变化而另一个变量的值不变.

问题7：这六个具体情境中变量之间的关系有什么共同特点吗？这种关系就是我们通常所说的函数关系，你能给函数下个定义吗？

生6：一个变量的值固定，另一个变量的值也随之固定.

【设计意图】环节2的目的是突破难点、抽象概括出“对于x的每一个确定的值，y都有唯一确定的值与其对应”. 突破难点的做法主要有以下两个方面.

一是创设第二组情境及设计相应的问题串. 第二组情境同样以图象、表格、表达式三种形式呈现，以让学生感受函数表达的多样性. 不同的是，该组情境中变量之间的关系与第一组情境“有所区别”. 对于该组情境，从函数图象来看，图象中有一段是一条平行于x轴的线段，是“平的”；从函数值来看，当自变量x在某个区间取值时，y的值始终是同一个常数. 学生依据日常生活经验认为，在该区间，x的取值改变了，但y的取值并没有发生变化. 因此，变量之间的关系用“一个变量随另一个变量的变化而变化”来概括就不恰当了. 那么如何描述呢？这就“逼迫”学生跳出“直观”，摆脱变量变化的物理背景，思考变量之间更为本质的关系：对于x的每一个确定的值，y都有唯一确定的值与其对应. 上述实录说明第二组情境的设置及教师用针对性的提问和追问，确实能够让部分学生更深入地思考，进而概括出该组情境的本质属性（虽然语言不够精确）.

二是师生对话，并辅以表格法. 由于学生的学习过程不仅仅是一个自我建构的过程，还是一个与他人交互的社会性建构过程. 因此，教师通过与部分学生的对话，借助表格，分别将每个情境中（x，y）的值尽可能多地列举出来，以让学生理解“对于x的每一个确定的值，y都有唯一确定的值与其对应”这句话的内涵.

环节3：函数定义、定义解析、函数定义演变史.

在该环节，教师给出教材中函数的定义，并对定义进行解析. 然后结合定义，对前述六个具体情境逐一剖析，以促进学生对函数概念的理解.

接下来，教师介绍函数定义的演变史，并将其与前两个环节的学习建立起联系，指出：数学家们用将近100 年的时间才抽象概括出来的函数定义，你们用了不到两节课的时间就能表达出大致意思，真的很棒，所以大家一定要对数学学习充满信心. 此外，上述函数定义的演变过程也说明，函数概念的形成不是一蹴而就的，是一个逐渐调整和完善的过程. 今天的学习过程也一样，我们也经历了历史上类似的过程，等到高中以后，大家还要继续学习函数的概念.

四、思考与建议

1. 充分认识到第一个层次抽象的重要性

史宁中教授将数学抽象分为三个层次：一是简约阶段，把握事物的本质，把复杂问题简单化、条理化，并能够清晰地表达；二是符号阶段，去掉事物的具体内容，利用概念、图形、符号和关系术语等表述已简约化的事物；三是普适阶段，通过假设和推理建立法则、模式或者模型，能在一般意义上解释具体事物.

上述数学抽象的三个层次的具体步骤如图3 所示. 从“辨别”到“抽象”为简约阶段，抽离事物本质；从“概括”到“形式”为符号阶段，完成符号表达；从“系统”到“运用”为普适阶段，形成理论并运用到具体情境.

图3

初中阶段函数概念教学主要包括上述（1）～（5），即主要涉及简约阶段和符号阶段，重点是简约阶段.

史宁中教授指出，第一个层次的抽象是极为重要的，但在我们的教学过程中往往被忽略. 因此，教师在函数概念教学中要充分认识到第一个层次抽象的重要性，给予第一个层次的抽象（即简约阶段）足够的重视.

2. 充分认识到第一个层次抽象的困难性

前述课前调研结果表明，学生很难抽象概括出教材中的函数定义. 但上述结论是基于所授课班级24名学生的调研结果，不具有代表性. 由于“历史上数学家所遇到的困难，正是学生也会遇到的学习障碍”，根据这种历史相似性，笔者查阅了相关数学史.

综观函数定义的发展史，可以发现，函数定义的抽象程度是逐步提高的. 1673 年，莱布尼兹创造了“函数”一词，表示任何一个随着曲线上的点变动而变动的几何量. 1755 年，欧拉指出，如果某变量以如下的方式依赖于另一些变量，即当后面这些变量变化时，前者也随之变化，则称前面的变量是后面变量的函数. 相比莱布尼兹的函数定义，欧拉的函数定义已经摆脱了具体的几何背景，涉及函数本质，这个本质就是刻画两个变量之间的变化关系. 因此，人们通常称欧拉的定义为函数的“变量说”. 1851年，黎曼给函数下的定义为：假定z是一个变量，它可以逐次取所有可能的实数值. 如果对它的每一个值，都有未知量w的唯一的一个值与之对应，则称w为z的函数，该定义被称为函数的“对应说”. 1839年，布尔巴基学派给出了函数的更为形式化的定义，被称为“关系说”. 可以看出，我国现行初中教材给出的定义融合了欧拉的定义和黎曼的定义. 而黎曼的定义摆脱了变量变化的物理背景，相比欧拉的定义更为抽象.

无论是课前样本的调研，还是函数定义的发展史，都在一定程度上说明了教材中的函数定义比较抽象，要归纳概括出来对于学生来说是比较困难的. 实际教学中学生的表现也印证了上述结论. 因此，教师要充分认识到第一个层次抽象的困难性.

3. 借助数学史，精心设计第一个层次的抽象的教学活动

德国数学家和数学教育家F.克莱因曾指出，生物发生学的一项基本定律指出，个体的成长要经历种族成长的所有阶段，顺序相同，只是所经历的时间缩短……笔者认为教授数学和其他任何事情一样，至少在原则上要遵照这些定律. 我国老一辈数学家余介石等也认为，历史之于教学，不仅在名师大家之遗言轶事，更可指示基本概念之有机发展情形，与夫心理及逻辑程序.

本教学设计就是从函数概念发展史中获得了启发，根据欧拉的定义和黎曼的定义，将第一层次的抽象细分为两个环节进行：第一个环节，回顾课前调研的那组情境，重点让学生抽象概括出该组情境的共同属性“都是一个变量随着另一个变量的改变而改变”，该环节对应欧拉的“变量说”定义. 第二个环节，设置了另一组情境，希望学生通过与第一组情境的对比，能够抽象概括出“对于x的每一个确定的值，y都有唯一确定的值与其对应”，该环节对应黎曼的“对应说”定义. 期望学生通过两个环节的递进学习，不仅能够抽象概括出教材中的函数定义，还能够理解教材中为什么如此定义函数.

课后对学生的访谈表明，上述两个环节的数学抽象过程给学生留下了深刻的印象. 尤其本节课前两个环节与数学史之间的联系，有效地激发了学生的学习兴趣和自信心，并使学生更深刻地理解了教材中的函数定义.

4. 借助单元设计，整体设计发展学生数学抽象素养的教学活动

素养的培养不是几节课就能立竿见影的，需要教师从长计议、整体设计. 为此，笔者将初中函数概念进行通盘考虑，构建了一个函数概念单元. 该单元除了函数概念外，还包括正比例函数概念、一次函数概念、反比例函数概念和二次函数概念. 在上述具体函数概念的教学中，均给出大量现实情境，要求学生写出变量之间的关系式，再判断变量之间是否满足函数关系，最后要求学生观察函数关系式的特点、抽象概括得到具体函数的定义. 这样处理的目的是希望通过具体函数概念的学习，进一步发展学生的数学抽象素养.

为了跟踪学生的学习状况，在学习每一个具体函数概念之前都对学生进行了前测，最后一次前测是在学习二次函数概念之前进行的. 由测试数据可知，学生抽象出二次函数概念的能力有所提高，但提高的幅度并不显著. 一方面，这说明了持续不断的、有针对性的教学对发展学生数学抽象素养是有一定效果的；另一方面，再次说明了数学抽象对于学生来说是比较困难的. 因此，培养学生的数学抽象素养需要教师持之以恒的努力.