基于脉冲神经网络的无线空中联邦学习

杨瀚哲，游家伟，文鼎柱，石远明

（上海科技大学,上海 201210）

0 引言

随着移动通信、物联网技术的发展，无线网络中的移动设备数量呈现指数级的增长，这些设备所拥有的海量计算和数据资源极大地推动了边缘人工智能在网络边缘的部署，从而为移动用户提供具有高可靠性、低延迟的智能服务，由此形成了一个新的研究领域，称为边缘机器学习[1-2]。

在众多的边缘机器学习框架中，应用最为广泛的是分布式的联邦边缘学习（FEL,Federated Edge Learning）[3-7]，它不需要用户上传自己的数据进行集中式训练，而是在每一轮的训练中，由一个中心服务器将全局机器学习模型广播给所有的设备，设备在本地训练该模型，得到局部梯度或新的局部模型并将该局部梯度/ 模型传回给中心服务器更新全局模型。这很大程度上保护了用户的隐私安全。但是，当前的联邦学习训练的往往是传统的深度神经网络模型，比如卷积神经网络。这些模型的训练需要在移动设备上消耗大量的能量、占据相当的计算资源。这大大限制了联邦边缘学习在边缘网络中的应用，尤其是当边缘设备为计算和能量资源受限的物联网设备时。除此之外，由于机器学习模型往往具有大量的参数需要传输，联邦学习需要消耗庞大的通信资源。

一方面，为了解决边缘设备能量和计算资源受限的问题，本文考虑在联邦学习系统中训练一种新的网络模型——脉冲神经网络（SNN,Spiking Neural Network）。脉冲神经网络是一种更加仿生的网络，它比起传统神经网络更加的节能[8-9]，并且有专属的硬件设备为其训练加速[10]。文献[11]的作者研究了基于脉冲神经网络的联邦学习，该文献指出，在联邦学习框架下，脉冲神经网络是可行的，而且比传统神经网络表现更加良好。另一方面，为了降低联邦学习训练的通信开销，本文将利用空中计算技术进行模型参数聚合。

为了提升联邦学习的性能，本文致力于最小化由空中计算所造成的模型参数失真，该问题为一个非凸的二次约束二次规划问题[12]。通过使用分支定界算法，本文提出了一种最优解决方案。最后，在基于CIFAR10 数据集的实验表明，所提出算法的性能优于其他已有算法，例如SDR[13]。

1 模型介绍

1.1 脉冲神经网络

考虑一个有J个隐藏层的脉冲神经网络，用Lj表示该网络的第j个隐藏层，其中的第i个神经元表示为ni,j。脉冲神经网络中每个神经元的输入与输出均为脉冲信号，如图1 所示。在这个网络中，每个输入数据被编码成长度为S的脉冲信号，并且逐个地输入进脉冲神经网络中。当2 ≤s≤S时，每个神经元的第s个时刻的脉冲信号由该神经元前一层的第s-1 个时刻的脉冲信号求得。把第s个脉冲信号所处时刻称为时刻s。在本文中，使用带泄漏整合发放模型（LIF,Leaky-Integrate-and-Fire）节点当作脉冲神经网络的神经元。

图1 脉冲神经元示意图

在一个训练轮次中，脉冲神经网络使用S个脉冲信号进行训练。在前向传播中的任意时刻，比如时刻s，每个神经元聚合所有的上一层的神经元在时刻s-1 的输出脉冲信号，并与该神经元本身在时刻s-1 的神经元隐状态（通常称作膜电位，用ui,j(s)表示神经元ni,j在时刻s的膜电位）聚合，得到该神经元在时刻s的脉冲输出（用oi,j(s) 表示神经元ni,j在时刻s的脉冲输出）。从而，神经元ni,j在时刻s的膜电位可以表示为：

其中，λ是衰减因子，i′代表Lj-1层的神经元的索引，wi′,i是对应关联的权重参数。对应的脉冲输出可以表示为：

如果在s时刻，该神经元的输出脉冲信号为1，则该时刻该神经元的膜电位会被重置为某一设定好的定值ur。

脉冲神经网络的反向传播与RNN 相似。考虑任意一个权重wi′,i，它连接了神经元ni′,j-1与ni,j。每个训练轮次中，它的梯度可以通过将所有时刻的梯度累加起来得到，即可以表示为：

其中L是损失函数。式(3) 中的主要的困难在于oi,j(s) 是不可微分的函数。为了解决这个问题，使用了替代梯度法[11]，即用阈值函数的逼近函数的梯度替代该梯度：

其中ξ是衰减因子，取决于脉冲信号的总长度S。对于很大的S，ξ应该是足够小的，以防止梯度爆炸问题，反之亦然。

1.2 联邦学习模型

考虑一个拥有多天线的边缘服务器与k个单天线设备的联邦学习系统。该系统的目的是通过共同训练一个脉冲神经网络来优化全局损失函数L，用公式表示为：

其中，w是脉冲神经网络的参数向量，L(w) 是用于分类任务的交叉熵损失函数，Dk与Lk(w)分别为设备k的本地数据集与局部模型的交叉熵损失函数，表示设备k的本地数据集的数量。具体而言，考虑任一训练轮次t，边缘服务器首先广播全局模型的参数wt-1给每个边缘设备。然后第k个设备基于收到的模型参数wt-1，用本地数据集Dk根据式(3) 与(4) 更新本地模型，并利用式(6) 计算本地梯度更新。

其中，gk(w) 为t轮次的设备k的本地梯度更新，wk,t为t训练轮次设备k完成本地训练后的本地模型参数，wt-1为t训练轮次开始时边缘服务器广播给各个边缘设备的全局模型的参数。最终，边缘服务器收集所有设备的本地梯度更新{gk(w)}，并用式(7)更新全局模型：

系统会重复上述步骤直至全局模型收敛。

1.3 空中计算模型

在每一轮次的训练中，服务器利用空中计算技术来聚合所有的本地模型参数，其接收信号可以表示为：

其中，hk∈CN为设备k与边缘服务器之间的上行信道向量，N为边缘服务器中的天线数量，bk∈C为传输标量，s k∈C为设备k的传输标志，是整合过后且归一化的本地梯度更新，假设它服从标准复正态分布，n～CN(0,σ2I)是高斯噪声。在式(8) 中，传输标志sk是复数标量，因此，每个标志可以分解为本地梯度更新中的两个元素：一个组成实部而另一个组成虚部。更多地，整个本地梯度更新向量的传输分布在多个资源块中，每个资源块中空中计算的设计是一样的。一方面，为了加快式(7) 中的梯度聚合，需要对传输标志进行预处理与后处理，过程为：

（1）预处理：设备k的本地梯度更新向量中的每个元素在传输前被除以一个因子因此，边缘服务器中没有任何误差的目标梯度聚合可以表示为：

（2）后处理：边缘服务器收集到的聚合信号需要进行处理以得到平均梯度，表示如下：

另一方面，在边缘服务器中，接收波束成形被用于预估式(9) 中的目标梯度聚合。加上波束成形后，边缘服务器中的接受信号可以表示为：

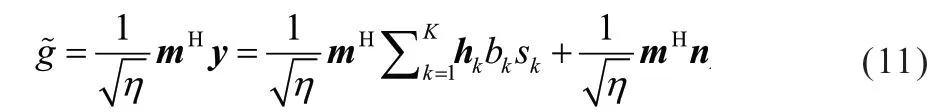
其中，m∈CN为接收波束成形向量，η为归一化因子。从而，式(7) 中的平均梯度聚合可以表示为：

2 空中计算与联邦学习

2.1 空中计算问题构建

本文的目标为目标梯度聚合与预估梯度聚合的最小化均方误差（MSE,Mean-Square Error），即式(9) 中的g与式(11)中的g～，可以表示为：

其中，函数MSE(x,y) 表示x与y的均方误差。此外，每个设备有一个传输能量约束：

其中，P0为每个设备的最大传输能量。

最终问题可以概括为：

2.2 问题简化

为了解决非凸问题P1，需要进行两步简化。首先，传输标量{bk} 可以被接收波束成形向量m表示。然后，问题可以被进一步简化成一个二次约束二次规划问题。第一步，根据参考文献[7,13]，对于任意一个给定的m，可以得到最小化均方误差的最优的传输标量，表示如下：

然后，考虑传输能量约束，可以进一步得到：

将式(17) 中的η与式(16) 中的bk带入式(13) 中的最小均方误差函数，可以得到：

其中，σ2是噪声的能量。由于σ、P0都是常数，P1 中的最小均方误差与下式是等价的：

第二步，根据参考文献[14]，式(19)中的问题可以进一步写成：

问题P2 是一个带着一个非凸约束的二次约束二次规划问题，这个问题是一个NP-hard 的问题。为了解决这个问题，文献[13]的作者们使用了一个基于SDR 与SCA的算法。但是，文献[13]中的算法只能得到一个次优解。本文中，参考文献[12] 采用分支定界法（BnB,Branch and Bound），它能保证得到问题P2 的一个全局最优解。

2.3 使用分支定界算法解最小均方误差

首先引入一个辅助变量x=[x1,x2,…,xK]T∈CK。使用该辅助变量可以将问题P2 转化成如下的等价的形式：

（1）第一步：集合X被分割成几个子集，每个子集对应着一个与P3 一样形式的子问题。

（2）第二步：解出每个子问题，以求出原问题的解的上下界。

（3）第三步：如果原问题的上下界收敛到同一个值，则原问题的最优解已找到。否则，在每个子问题上重复步骤1 与步骤2。重复以上步骤直至收敛。上述三个步骤的具体过程为：

其中，为集合S的凸包。用问题P3.1i的解作为问题P3i的一个下界，因为取问题集合中 最小的下界作为当前问题P3 的下界Lt。为了得到上界Ut，可以选择任意一个在问题P3i的可行域内的解当作一个上界。在这里，放缩问题P3.1i的最优解来生成一个可行的问题P3i的解的上界，如下所示。

把他们加入问题集合{P3i}，并且移除问题P3it。当然，也需要求得这两个问题的解的下界。在每个迭代轮次，得到新的问题集合{P3i}，并且得到该问题集合的上界Ut与下界Lt。停止迭代直到并选择与Lt对应的m作为问题P3 的解，否则继续迭代。

3 实验结果

3.1 实验参数设定

本文使用的神经网络模型为18 层残差结构的脉冲神经网络（即将标准ResNet-18 网络的全部激活函数替换为SNN 神经元）。每个训练轮次中，设定总的时刻数为10，并使用泊松编码器对CIFAR10 数据集进行脉冲信号化。为了简化问题，所有设备使用相同的学习率0.01。使用batch-SGD 训练神经网络，batch-size 为128。每个局部模型将会在边缘设备本地迭代5 轮。

与此同时，通信模型使用三维模型设定。边缘服务器被设定为位于坐标(0,0,20)，而其他设备均匀分布在以(120,20,0)为中心、半径20 m 的圆形区域内。距离相关的大规模衰弱被设定为其中T0是参考距离为d0=1 m 时的路径损失，d表示传输设备与接收器之间的距离，α是路径损失指数。除此之外，小规模衰落被设定为Rician 因子为β的Rician 衰落。平均500 个信道模拟的结果得到最终的信道向量。设定α=3，T0=-30 dB，β=3，

3.2 分支定界算法的有效性

图2 展示了分支定界算法的收敛性。可见，分支定界算法在300 轮迭代内达到收敛。

图2 分支定界算法的收敛性

之后，将分支定界算法与广泛使用的SDR 算法进行比较，如图3 所示。使用的指标为空中计算噪音范数（NOAN,Norm of AirComp Noise），定义如下：

其中，g为目标函数，为目标函数的估计值，该估计值使用如上文所述方法生成信道向量hk，并使用分支定界算法解出波束成形向量m。如图3 所示，分支界定算法的NOAN 一直比SDR 算法的要更小，证明分支定界算法的效果要比SDR 更好。

图3 分支定界算法与SDR的空中计算噪声范数比较

3.3 空中计算辅助脉冲神经网络的联邦学习框架的性能评估

空中计算辅助基于脉冲神经网络的联邦学习框架的性能如图4 所示。

图4 空中计算辅助基于脉冲神经网络的联邦学习框架性能评估

将本文使用的分支界定算法与标准模式和SDR 算法进行比较。其中，标准模式指直接使用目标函数值作为空中计算的结果，而SDR 算法指使用SDR 算法解问题P2 所得到的空中计算结果。由于分支定界算法得出的解是全局最优解，所以当σ2很小的时候训练曲线更加接近标准模式。然而，随着σ2增加，收敛速度变得很慢，并且最终准确率也比标准模式要低。另一方面，与只能求得局部最优解的SDR 对比，本文的算法在收敛速度与准确率上明显表现更好。

4 结束语

本文中，研究了基于脉冲神经网络的无线空中联邦学习框架，并提出了相应的解决算法。由于脉冲神经网络相较于传统神经网络计算效率更高且更加节省能量，所以该框架比基于传统神经网络的联邦学习框架更加具有实践意义。同时，使用的空中计算技术也很大程度上降低了通信消耗，弥补了联邦学习在通信传输资源消耗方面的缺陷。大量仿真结果显示，所提出的全局最优的分支定界算法各方面表现都比局部最优的SDR 算法要好，并且基于分支定界算法的收敛速度与准确率都优于基于SDR 的算法。在未来的工作中，可以考虑比较不同网络模型（如CNN、SNN）在不同应用场景下的性能下界，从而根据场景选择合适的模型。总而言之，SNN 的引入为6G 联邦学习带来了更多的可能性，在未来也会有越来越多的工作对基于SNN 模型的联邦学习应用进行研究。