基于分形特性的开口拱形结构风致积雪漂移风洞试验研究

姜昕彤，曹 兵，崔翰博，黄 博，杜怡韩，王家伟

(安徽工程大学 建筑工程学院，安徽 芜湖 241000)

开口结构多被运用于剧院、教堂和体育馆等公共建筑中。洞口处积雪分布形态不同于封闭表面，周边积雪易产生不均匀分布，对结构安全性不利。相邻开口结构间的风雪运动由于相互遮挡作用也更为复杂，并非单独两个结构周围风雪运动的叠加。此外，开口结构表面不均匀积雪分布系数无规范可循。因此，需明确此类结构表面及周边风雪运动规律，以期提高对雪颗粒的空间分布形态预测的准确性。

研究风致积雪漂移最可靠方法是利用风洞进行缩尺试验。风洞试验首先要满足相似理论。Anno[1]和Lever[2]等对不能同时满足雷诺数和弗劳德数的问题进行分析，最终认为大密度粒子在满足雷诺数相似情况下试验结果与实测值更吻合。刘盟盟等[3]基于上述相似参数进行了缩尺试验，结果发现，应用跃移层质量传输率相似准则可精确还原实测结果的积雪分布形状。通过雪粒及相似粒子的研究得出，石英砂粒子的各项参数均能较好地模拟雪粒子[4-6]。部分学者针对屋面坡度与其他影响因素之间的关系及对积雪分布的影响进行研究。Zhou等[7]得出不同屋顶坡度（5°～60°）条件下的屋面积雪分布形态，发现临界屋顶坡度在20°～25°；刘博雅等[8]发现高跨屋面跨度对屋面变跨处的积雪分布影响最为明显，高跨为60°的双坡屋面，在迎风向3 m/s风速时变跨处积雪分布系数最大；Cao等[9]发现屋面坡度对结构背风面雪深影响极大，迎风面雪深受风速影响较大。Zhou[10]、Zhu[11]等分别以平屋面和阶梯式平屋面为研究对象，总结了有降雪和无降雪两种情况下屋面积雪的分布规律，例如，Zhou等[10]发现屋面积雪侵蚀程度与降雪强度之间的关系具有明显的线性特征。一些学者对不同影响因素下结构表面的积雪特征进行了研究。Liu等[12]研究了模型尺寸和风速不同条件下，考虑雪残率和侵蚀率时，积雪分布规律对屋面的影响；Yu等[13]探讨了模型尺寸、风速、吹风时间对积雪形态特征的影响；Jiang等[14]分析了体育场开口方向、场馆间距和风向角对建筑屋面及周边积雪特征的影响；Liu等[15]指出不均匀积雪分布与风速和屋顶间距密切相关，屋顶上的盾形或其他凸出物对屋顶积雪模式产生影响；王建烁等[16]研究得出试验时长对积雪厚度影响极大，但对屋面的积雪范围影响较弱。

关于积雪分布形态，多数学者采用雪深系数对其进行表示[12,14]，并无可描述粒子覆盖区域综合特征的物理量。Mandelbrot[17]提出了分形理论这一概念，既能有效度量自相似性结构，又可定量描述不规则物体的几何形体和组成[18]。近年来该理论已较好地应用在多孔介质结构面如煤[19]、花岗岩[20]、混凝土[21]等结构表面的粗糙程度的研究中。分形维数是分形理论的定量表征，已有专家将其应用于湍流领域，李正农等[22-23]考虑了不同风场类别、风压变异系数、风压系数功率谱与风压分形维数之间的联系。袁全勇等[24-25]得出风速时间序列曲线的分形维数、地表粗糙度和湍流强度之间均呈正相关性。王广等[26-27]采用多重分形方法研究了地表粗糙度对风速时间序列分形维数的影响，发现结构函数法求出的分形维数误差较小。

综上可看出，目前风致积雪漂移的研究对象大多是简单类型的结构屋面，如平屋面、单双坡屋面、球形屋面等。而针对开洞口结构的设计如果套用上述规律，则与工程实际情况不符，存在极大安全隐患。相邻结构及典型开口结构（周边及表面）的积雪不均匀分布情况较为复杂，目前《建筑结构荷载规范》规定的积雪分布系数对其并不适用。此外，风吹后的积雪表面粒子分布特性极为复杂且无规律可循，前人大多通过研究粒子特性指标来反映整个区域的综合形体特征或分布规律，这种研究方法需要大量数据作为样本，存在测量工作存在周期长、费用高等问题。因此，本文首先以开口拱形屋面结构为研究对象，研究了洞口方位对单独拱形屋面表面及周边积雪分布的影响，结构间距和洞口角度对双开口拱形结构间积雪分布形态的影响及相互干扰效应。然后，基于风洞试验数据，引入了分形理论进行量化分析，得到的粒子分形维数可作为判定不同因素对积雪分布形态影响程度的重要结论，以期为准确描述雪粒分布形态特征的研究提供一种新方法。该研究细化了开口结构风致积雪漂移的影响参数，揭示了不同因素下积雪分布的变化规律，完善了此类带有开口的新型建筑结构周边及表面的抗风、雪设计，有效提高了此类开口结构的经济性、安全性和规范性，有良好的工程应用前景。

1 风洞试验及基本理论

1.1 试验仪器

小型低速直流风洞总长为7 m[28]，由风机、稳定段、收缩段、试验段和扩散段组成，具体如图1所示。试验段长1.5 m，截面为正方形，尺寸为0.5 m×0.5 m，试验段内稳定风速为1.5～10.0 m/s。经测定，该风洞试验段的气流稳定性不高于1.5%，动压场系数小于2%，湍流度小于2%。对照点取屋面高度10 cm处，采样时间3 min，分别测量原始风速为3、4、5、6 m/s时的流场数据，对应的风速依次为2.76、3.89、4.83、5.91 m/s，平均风速剖面和湍流强度剖面如图2所示，图2中实线为拟合曲线。

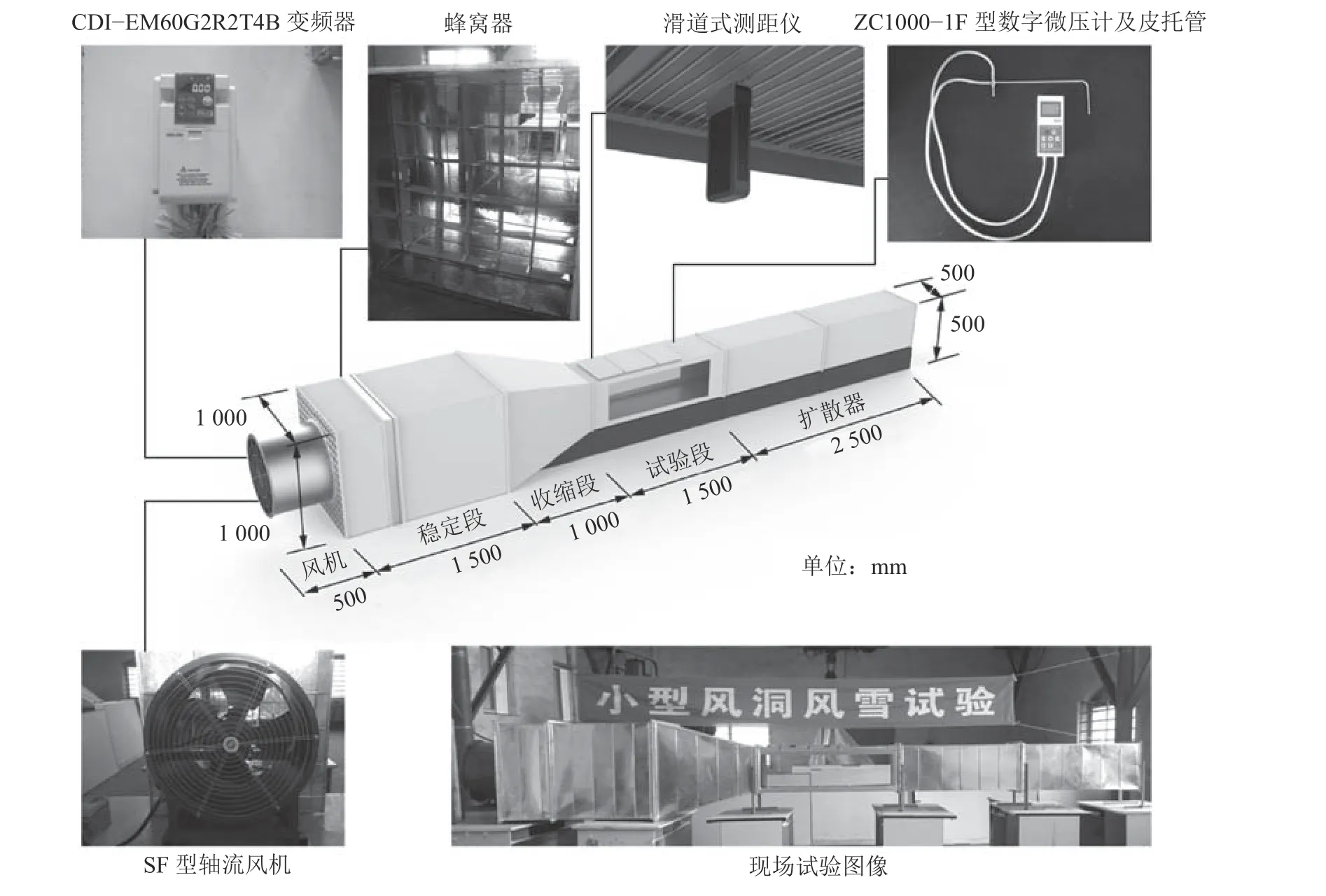
图1 小型低速直流风洞Fig. 1 Small low-speed DC wind tunnel

图2 平均风速剖面和湍流强度剖面Fig. 2 Average wind speed and turbulence profile

1.2 基本理论

1.2.1 相似理论

风洞试验首先需满足几何相似，根据模型和原结构的几何尺度和特征尺度比率相等，得出：

以时间平均结果为目标的风洞试验中，一般可忽略湍流特性和积分尺度的运动相似[30]。而动力相似是风洞试验相似原理的重要参数之一。风雪作用气固两相流运动因机理十分复杂，现阶段的风雪风洞试验针对动力相似还未有统一标准，但许多学者采用的重要模型参数已趋于一致，气动阻力相似条件满足：

质量输运率需满足式（10）和（11）：

目前，尚未见文献报道有针对结构面雪粒分布规律进行研究的分形维数公式。通过对比发现，粒子的蠕移运动形式与岩石的节理表面形态较为相似，两者都属于自然分形，且粗糙程度较大，故采用谢和平等[33]提出的经验公式来计算雪粒的分形维数：

式中，D为分形维数，h为平均高度，B为平均基长。

2 试验概况

2.1 试验方案

选取单独拱形屋面结构为试验对象，研究不同洞口方位（洞口位于迎风面、侧立面、背风面、无洞口）对结构屋面及周边积雪分布的影响。其中无洞口情况分为工况1（风向平行于屋面坡度）和工况2（风向垂直于屋面坡度），如图3所示。

图3 无洞口两种工况Fig. 3 Two working conditions without opening

以相邻开口拱形屋面为研究对象，分析不同间距和相对角度下，结构表面的积雪分布形态及结构间的相互干扰效应，试验方案如表1所示。研究双模型相对角度时，洞口直线距离s为100 mm，相对角度α为变量，如图4所示。

表1 试验方案Tab. 1 Test plan

图4 双拱形屋面结构相对角度说明Fig. 4 Explanation of the relative angle of two arched structures

2.2 试验内容

采用石英砂预铺的方法，模拟风吹雪形态，在试验模型来流区域，覆盖0.3 m长的石英砂粒子，用来模拟积雪边界，此方法可同时加速边界层的发育。在风洞出口下端套置0.5 m×0.5 m×1.0 m的简易箱，作用是收集风洞吹出的沙粒，用来计算质量输运率。具体试验内容如下：

1）试验模型选取。模型为拱形屋面结构，由15 mm厚的胶合板制成，用玻璃胶粘合并镶嵌钢钉加固。模型下部边长150 mm×150 mm，洞口尺寸20 mm×20 mm，开口位置及具体尺寸如图5所示。

图5 拱形屋面结构轴测图Fig. 5 Axonometric drawing of arched structure

2）石英砂粒子基本性质测定。对选用的石英砂粒子进行测定，测得颗粒平均粒径为0.14 mm，休止角为30.8°，密度为2.56 g/cm3，阈值速度u*t、u3*t/2gv、u*/u*t等相似参数均满足要求，但由于沉降速度wf较大，wf/u*和wf/u*t均大于原型值。

3）试验时间、速度及颗粒预铺厚度测定。根据Oikawa等[34]的现场实测气候数据模拟真实风吹雪过程，地面粗糙度为A类，最大降雪深度为200 mm，几何缩尺比为1/10，粒子厚度为20 mm。实测过程中，风速大小随时发生改变；结合相似准则及实测平均风速，试验风速确定为4.5 m/s；由时间尺度相似，试验时间设为9 min。

4）石英砂粒子的测量。选用滑道式红外线测距仪对积雪厚度进行测量，测量精度±0.1 mm。试验前将激光测距仪垂直布置于滑道上，对各点高度进行测量，最终得到粒子深度为：

式中，h0为 试验前积雪面到测距仪的高度，h1为试验后积雪面到测距仪的高度。

2.3 小型低速直流风洞准确性验证

试验模型与Oikawa等[34]实测立方体模型相似，边长为1 m×1 m×1 m，几何缩尺比为1/10，因此，试验模型尺寸为0.1 m×0.1 m×0.1 m，粒子厚度为20 mm，试验时间及风速如第2.2节所示。Oikawa等[34]实测了7种不同工况下的立方体降雪深度，场地实测情况如表2所示。

从表2可以看出，仅SN09和SN36两种工况基准点降雪深度为200 mm，且两种工况下立方体周边的雪深系数变化规律趋势一致。故仅以工况SN09为例，取实测值x/H=-1.5～3.0范围内的雪深系数进行对比试验，其中，x为变量，指立方体横向坐标。以立方体高度作为特征尺度进行x的无量纲化，以粒子初始深度作为特征尺度将颗粒最终深度进行无量纲化，得到雪深系数Cs。风洞试验值与文献[34]实测值对比结果如图6所示。

图6 试验结果与Oikawa[34]实测结果比较Fig. 6 Comparison of test results with Oikawa’s[34] actual test results

表2 场地实测情况[34]Tab. 2 Field measurements[34]

由图6得出：在模型迎风侧，实测所得雪深系数先减小后增大，雪深系数的最小值出现在x/H=-0.8附近，最小雪深系数为0.55。试验得到的雪深系数呈增长趋势，x/H=-1.5时雪深系数最小，最小雪深系数约为0.55。由此可知，两种情况下最小雪深系数出现位置不同，在模型迎风边缘（x/H=-0.5处），两者的雪深系数数值差异在可接受范围内。在模型背风区域，两种情况的雪深系数均先减小后增大，变化规律基本一致，但数值存在差异。这是由于实测时的风向是随机变化而不是始终垂直于模型迎风面，风速大小也是不确定的，故在迎风区域最小雪深系数的出现位置和雪深系数数值大小存在一定差异，但对所得规律影响较小，故认为试验值与实测值基本吻合，该小型直流风洞可用于风致积雪分布的研究。

3 试验结果分析

3.1 洞口方位的影响

分别对洞口位于拱形屋面结构迎风面、背风面、侧立面及无开口拱形结构进行试验，得出不同条件下雪深系数的分布曲线，其中，因拱形屋面坡度不同，将无开口模型分为两种工况进行试验，工况1方向如图3（a）所示，工况2方向如图3（b）所示，横纵坐标定义与第2.3节相同。其中，颗粒沉积时雪深系数大于1，侵蚀时雪深系数小于1。拱形结构屋面及周边积雪分布曲线如图7所示。

由图7（a）得出：在拱形结构迎风侧中轴线上粒子发生侵蚀，背风侧中轴线上粒子发生沉积，且沉积量较大，此变化规律与立方体周边粒子分布规律相似。在拱形结构背风边缘（x/H=0.75处），除洞口位于侧立面时，其他4种条件下积雪均堆积在结构边缘，雪深系数数值约为1.0～1.2，此区域不建议设立紧急疏散通道等设施。在远离拱形结构中轴线上，雪深系数先减小后增大又减小，呈波纹形式变化，即粒子发生蠕移运动。无洞口工况1的拱形坡度与洞口位于迎风面和背风面时相同，无洞口工况2的拱形坡度与洞口位于侧立面时相同，在拱形结构背风侧中轴线上，拱形结构洞口位于背风面的雪深系数小于洞口位于迎风面和无洞口工况1的雪深系数，洞口位于侧立面的雪深系数小于无洞口工况2的雪深系数。且洞口位于侧立面工况下的雪深系数数值均不大于1，说明粒子发生侵蚀，因此当洞口位于侧立面，对拱形结构中轴线上的积雪分布最为有利。

由图7（b）得出：在纵向轴线上，拱形结构迎风前沿（x/H=-0.75处）产生两个经典马蹄状旋涡，此后在顺风向临近区域和拱形结构背风侧的粒子均呈波纹式增大，纵向轴线上粒子的蠕移运动比中轴线上更为剧烈。在x/H=-0.25～4.00这一区间，工况1的雪深系数明显大于洞口位于侧立面工况，两者在x/H=1.75处最高相差可达28%。结合图7（a）、（b）可知，拱形结构周边雪深系数受洞口方位影响较大，洞口在侧面时无论是中轴线还是纵向轴线的雪深系数均小于无洞口工况相同位置雪深系数，故洞口位于侧立面时，对开口拱形结构周边积雪分布是有利的。

由图7（c）得出：在不同洞口方位条件下，拱形结构表面的粒子均发生侵蚀，对结构屋面稳定性是有利的，拱形结构表面雪深系数最大值出现在x/H=-0.25处，最大雪深系数在0.7～0.9之间，洞口位于迎风侧的雪深系数比无洞口工况2雪深系数高约22.2%。因此应探究积雪不均匀分布对屋面安全性所产生的影响。

图7 拱形结构屋面及周边积雪分布曲线Fig. 7 Distribution curves of the snow on the roof and the surrounding area of the arched structure

3.2 间距的影响

以洞口相对的相邻开口拱形屋面为研究对象，其间距L依次为50、75、100、125和150 mm，得出拱形结构中轴线、纵向轴线及表面的积雪分布，中轴线及纵向轴线的选取在图中已标出。拱形屋面中轴线雪深系数分布曲线如图8所示。

图8 拱形屋面中轴线积雪分布曲线Fig. 8 Snow distribution curves on the central axis of the arch structure

由图8（a）得出：在模型1迎风边缘（x/H=-0.75处）中轴线上的雪深系数值为1.05，表面粒子在此处发生沉积；模型1背风边缘（x/H=0.75处）中轴线上的雪深系数值为1.25～1.45，粒子在此处沉积较为严重。此外，相邻拱形结构间的粒子也发生较大面积沉积，且拱形结构间距越小，雪深系数越大。模型2迎风面边缘积雪沉积较大，间距为50 mm的雪深系数约为间距为150 mm的雪深系数的1.14倍；在x/H=1.25处二者相差最大，约为1.19倍左右。

由图8（b）得出：模型2背风边缘（x/H=0处），雪深系数值介于1.20～1.35间，此处粒子发生沉积；在x/H=1.75处，间距为50 mm和150 mm时，雪深系数的差值达到最大，接近26.67%。综上得出，相邻开口拱形结构中轴线上的雪深系数随间距增大而减小，间距为50 mm时中轴线上的积雪分布形态对于两开口拱形结构的稳定性最为不利。

研究不同间距下拱形屋面纵向轴线上的积雪分布情况，分为模型1周边和模型2周边两种情况，如图9所示。

图9 拱形屋面纵向轴线积雪分布曲线Fig. 9 Snow distribution curves on the longitudinal axis of the arch structure

由图9（a）得出：在迎风区纵向轴线上，模型1的迎风边缘（x/H=-0.75处），形成两个经典马蹄状旋涡，此时积雪发生侵蚀；相邻区域雪深系数迅速增大，在x/H=-0.25处，积雪厚度的增幅极为明显，应注意此处积雪突变产生的不均匀分布对拱形结构侧壁面的影响；在x/H=-0.25～0.75间，粒子一直沉积在结构周边，因此拱形结构侧壁将承受较大雪压。

由图9（b）得出：由于模型1的遮挡作用，模型2周边纵向轴线上的积雪分布不同于单独拱形结构，相邻拱形结构间的风雪作用更为复杂，因此在此种建筑群形式的设计中应着重考虑风雪作用产生的影响。模型2迎风边缘（x/H=0处）的间距为50 mm时，雪深系数高于间距为150 mm的雪深系数，高约24.14%；在模型2周边（x/H=0～1.5）的积雪也发生较为严重的沉积，故模型1的遮挡作用对模型2极为不利，应注意被遮挡拱形结构周边的积雪分布对侧壁面的影响。由图9还可得，在纵向轴线上雪深系数随间距的增大而减小，此规律与拱形结构中轴线的积雪分布规律相同。

研究间距对拱形结构表面积雪分布的影响，如图10所示。

图10 拱形结构表面积雪分布曲线Fig. 10 Snow distribution curves on the surface of arched structure

由图10可知：两个拱形结构表面粒子均发生侵蚀。对比图7（c）和图10（a）可以看出，位于迎风上游区域的模型1表面粒子分布形态与单独结构存在差异，说明不同建筑间风雪运动相互间产生了影响。模型1与模型2表面的积雪分布形态也完全不同，相同测点条件下模型1表面的雪深系数整体高于模型2。此外，模型1表面中心部位（x/H=-0.25～0.25）的粒子量明显多于其他区域，而模型2表面在x/H=-0.25～0间的粒子量相对较多，这也验证了起遮挡作用的拱形结构对被遮挡拱形结构表面的积雪分布形态产生了较大影响这一结论。

3.3 洞口相对角度的影响

研究洞口相对角度 α分别为15°、30°、45°、60°、75°时，拱形结构中轴线及纵向轴线上的雪深系数变化情况，如图11所示。其中，拱形结构摆放位置如图4所示，因5种相对角度下模型2表面的积雪分布与第3.2节存在较大不同，故仅对相邻拱形结构周边及模型2表面区域雪深系数进行分析。

图11 两开口模型不同洞口角度积雪分布曲线Fig. 11 Snow distribution curves of two opening models with different opening angles

由图11（a）得出：在模型1中轴线背风边缘（x/H=0.75处）的雪深系数介于1.25～1.40之间，高于模型2迎风边缘（x/H=1.75处）的雪深系数值（1.05～1.35）；当相邻拱形结构相对角度接近30°时，其周边粒子深度高于其他条件下，模型1背风边缘（x/H=0.75处）相对角度为30°的雪深系数高于相对角度为75°时雪深系数，高约22.22%；相邻拱形结构洞口角度为75°时，两模型中间区域和模型2背风面粒子的厚度最小。

对比图9（a）、（b）与图11（b）能够发现：相邻拱形结构相对角度发生变化时，模型2周边的粒子分布规律不同于拱形结构并列排布时的分布情况，模型2迎风边缘（x/H=-0.75处）与模型1相似，也产生了旋涡，但旋涡的面积小于单独结构条件下，粒子在此处并未全部被侵蚀，雪深系数值均大于0；在x/H=-0.25处，雪深系数迅速增大到1.05～1.35，此后粒子一直沉积在拱形结构周边及模型背风区域。相邻拱形结构相对角度为30°时，粒子出现了最不利分布形态，应在工程设计中避免这种排列分布方式。

由图11（c）得出：不同条件下位于迎风下游的拱形结构表面粒子分布形态各不相同，屋面的粒子量明显小于迎风上游的拱形结构，雪深系数峰值产生区域也有不同，究其原因是因为模型2的排布位置差异，使得模型1遮挡位置改变，模型2表面的风雪流轨迹也随之产生变化。除相对角度为15°外，其他4种相对角度下结构表面的积雪均有一部分被吹离表面，侵蚀面由高至低依次为75°、60°、45°、30°。相对角度为15°时，最大雪深系数出现在x/H=0处，其值为0.6；其他相对角度下的最大雪深系数均出现在x/H=0.25处，其值介于0.2～0.4间；相对角度为75°时最大雪深系数值最小，为0.2。总体来说，模型2表面的粒子均发生侵蚀，且侵蚀量较大，因此对屋面稳定性影响不大。

3.4 粒子的分形维数

由于风洞试验中考虑间距这一影响因素时，相邻拱形结构间距离是变量，测点的选取无法统一，故仅在洞口方位和相对角度这两种影响因素下进行粒子特性分析。具体可分为中轴线和纵向轴线两种情况，以得出更全面的粒子特性指标，同时可用来反映整个区域的综合形体特征，也可判定两种因素对积雪分布形态所产生的影响程度。粒子分形特性变化规律如图12所示。

由图12可得，相同条件下基于洞口方位和相对角度不同，中轴线和纵向轴线生成的粒子间分形维数各不相同，在同一洞口方位或相对角度条件下，纵向轴线的粒子分形维数明显高于中轴线处，说明拱形结构背风纵向周边区域积雪形态的粗糙程度远高于中轴线区域。

图12 粒子分形特性变化规律Fig. 12 Change law of particle fractal characteristics

由图12（a）可知：位于中轴线的粒子分形维数中，无洞口工况1的分形维数值最大，值为1.657；其次为洞口位于迎风面的分形维数值，为1.636；洞口位于侧立面的分形维数值最小，为1.490。所得结论与图7得到的规律相近，因此局部区域与粒子整体覆盖区域的积雪分布特征在一定程度上相似。另外，各条件下位于纵向轴线的分形维数值差异较小，说明风对粒子产生的冲击、搬运及堆积效果不明显。从积雪分布整体区域来看，洞口位于侧立面时的积雪粗糙程度最小，对地面雪压的影响最为有利。

由图12（b）可知：纵向轴线整体的粒子分形维数变化规律与图11（b）的变化情况并不相同；模型2周边局部粒子的雪深系数，在相对角度30°时最大，在75°时最小；但纵向轴线整体区域中最不利的相对角度为60°，分形维数值约为1.163，其次为30°。另外，相对角度60°时的雪深系数变化幅度最剧烈，说明此时风对雪粒子的扰动极大，区域粗糙度要高于其他工况，但最大雪深系数要低于30°和45°时所测的数值。

对比不同影响因素下的粒子分形特性，发现洞口方位纵向轴线的分形维数（1.856～1.873）远高于相对角度时所测数据（1.118～1.163）；而洞口方位中轴线的分形维数（1.490～1.657）远高于相对角度条件下（1.024～1.040）。可见，洞口方位对结构整体积雪分布的影响程度要高于相对角度。

4 结 论

通过风洞试验对拱形结构的风致积雪漂移过程进行探究，得出了结构周边、表面的局部雪深系数。结合两种影响因素下粒子的分形特性，得到了整体区域粒子分布的粗糙度特征，具体结论如下：

1）拱形屋面迎风边缘角部积雪完全侵蚀，结构背风侧积雪全部沉积，呈波纹形式变化。

2）单独拱形结构当洞口位于侧立面时，积雪分布较为有利，洞口位于迎风面最为不利。

3）相邻拱形结构洞口相对时的风致积雪漂移运动并不是单独拱形结构风雪作用的简单叠加；相邻拱形结构间的雪深系数随间距减小而增大；相邻拱形结构洞口相对角度为30°时，拱形结构周边积雪分布对结构最为不利。

4）洞口方位较相对角度对结构周边积雪分布形态的影响更大。

5）洞口位于侧立面时，积雪粗糙度情况对地面雪压的影响最为有利；相对角度为60°时，分形维数最大，但局部最大雪深系数低于30°。