超声波频率对油井套管清蜡效果影响的研究*

张紫衡 姜民政 董康兴 任智慧 赵 喆

(1.东北石油大学机械科学与工程学院 2.中国石油勘探开发研究院)

0 引 言

随着我国诸多油田开采进入中后期，各大油田相继采用水驱、聚驱及三元复合驱等采油工艺以提高原油采集量[1]。然而，在各大油田对上述采油工艺使用量逐年提升的大背景下，这些工艺所衍生出的问题也逐渐暴露出来，即在同一检测周期内，在使用上述采油工艺后，油井套管积蜡率相较于使用常规手段开采后的积蜡率有着显著上升[2]。油井套管积蜡现象对油田的安全和高效生产造成严重威胁，而这一问题的出现，始终困扰着相关科研与工作人员。

目前，传统的油井套管清蜡工艺主要分为3类：热油循环清蜡法、化学清蜡法和机械清蜡法[3]。上述清蜡工艺在面对多种工况时普遍存在适应性差、智能化程度低、单次作业成本高和对环境污染性大等缺点。相比于传统的油井套管清蜡工艺，超声波油井清蜡工艺以其良好的工程适应性、智能化程度高及对环境污染性小等诸多优势，近年来在我国各大油田得到了应用与推广[4]，效果也获得了一定认可。

超声波之所以能够应用在油井套管清蜡领域，主要归因于超声波所具有的机械能效应和空化效应[5]，而超声波频率的变化会对上述两种效应造成不同程度的影响[6]。因此，选择合适的超声波频率对解决超声波技术在油井套管清蜡领域中的应用显得尤为重要。李丹[7]提出超声波频率在28 kHz时防除垢效果较强；叶鹏等[8]提出超声波频率为28 kHz时除垢率最高。前述研究存在的问题是：超声波最适合的清蜡频率的确定是在某种特定条件下设计的试验，并通过对数据分析处理得到的结论，缺少普适性及系统的理论支撑。

鉴于此，笔者以Huygens-Fresenl理论为研究基础[9]，首先建立了非点声源(超声波)声场积分模型，推导了声压、声强及声场指向性系数的表征函数，并结合实际工况，考虑了声衰减的问题；随后选取6组工业中常用的超声波频率，利用数值分析软件Comsol和Matlab，分别对表征函数与声衰减现象之间的关系进行了数值计算与仿真分析。所得结论可为超声波技术在油井套管清蜡领域中的应用奠定基础。

1 超声波声场理论

1.1 非点声源(超声波)声场积分模型建立

声场主要是指声波在某一介质传播过程中所形成的空间范围，从超声波在油井套管清蜡工程应用的角度来讲，超声波的声场越强，所反映出的清蜡特性越强[10]。在Huygens-Fresenl理论中[9]，为客观描述某一超声波声场，需先建立非点声源(超声波)声场积分模型，并通过对点声源[11]积分的方式，推导出该超声波声场的声学特性。

根据Huygens-Fresenl理论，建立如图1所示的非点声源(超声波)声场积分模型坐标示意图。在该示意图中，假设在一无衰减介质中的超声波换能器半径为a，取超声波换能器中心点O为坐标系原点，以换能器所在平面XOY平面和垂直于XOY平面并穿过中心点O的轴线为Z轴建立空间坐标系。在此空间坐标系中，可将每一个小面元ds视为一个点声源，φ为X轴与ds间夹角。在YOZ平面内，设置一远场观察点P，P点与中心点O的距离为r，与ds的距离为h。声波辐射角θ为r与Z轴之间的夹角，小面元ds极角为α，极径为ρ。

图1 非点声源(超声波)声场积分模型坐标示意图Fig.1 Schematic coordinates of non-point source (ultrasonic) sound field integral model

1.2 非点声源(超声波)声场表征函数

在声学的理论研究和实际应用过程中，通常会引入声压、声强及声场指向性系数等相关表征函数来客观描述某一非点声源(超声波)声场的相关声学特性[12]。

1.2.1 非点声源(超声波)声压函数

声压是指声波通过某种介质时，由振动产生的压强改变量。根据点声源声压公式[13]，可得到ds在P点处的声压p1表达式为：

(1)

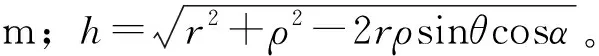
对式(1)进行积分，得到整个超声波换能器面辐射声压p2为:

(2)

根据Bessel函数性质[14]，对式(2)积分即可得到非点声源(超声波)声压函数p的表达式为：

(3)

式中：J1为1阶Bessel函数。

1.2.2 非点声源(超声波)声强函数

声强是指声波平均能流密度大小。结合超声波技术在油井套管清蜡领域的运用，即可说明在同一功率下，声波的声强值越大，所表征超声波的清蜡效果越好[10]。

根据声强定义，声强能通过在一定时间内单位面积上声波在传播过程中向邻接介质所做的功表示[13]：

(4)

式中：Re(p)为声压p函数实部,Pa；Re(c0)为声音在介质中传播速度c0的函数实部，m/s。

将式(3)代入式(4)可得非点声源(超声波)声强函数表达式为：

(5)

1.2.3 非点声源(超声波)声场指向性系数

声场指向性主要表征声音在某一介质中的传播范围与传播能力，目前常用声场指向性系数来表示声场的分布情况。点声源声场指向性系数表达式为[13]：

(6)

式中：pref为选取参考点的声压值，Pa。

取pθ=0°为pref，求得当θ=0°时，pθ=0°为：

(7)

将式(3)和式(7)代入式(6)中，可得当θ=0°时，非点声源(超声波)声场指向性系数为：

(8)

1.3 超声波在非理想介质传播过程中的声衰减

当超声波应用在油井套管清蜡领域中时，由于超声波的传播介质为含有杂质的非理想介质[15]，所以超声波在传播过程中会随着传播距离的增加而逐渐衰减。在经典声吸收理论中，声吸收系数αs用以表述声波振幅随距离衰减的快慢程度，αs值越大，声波衰减程度越快。声吸收系数αs常用斯托克斯-克希霍夫公式表示[13]：

(9)

式中：η′为切变黏滞系数；χ为热传导系数；CV为定容比热容，J/(kg·℃)；CP为定压比热容，J/(kg·℃)。

一般情况下，在液体介质中，相比于黏滞引起的声衰减，热传导的吸收系数贡献很小，通常可以忽略。因此，在忽略热传导系数的情况下(设χ=0)，将ω=2πf代入式(9)中，得到声吸收系数公式为：

(10)

2 基于Comsol与Matlab的数值模拟

2.1 压电式换能器仿真模型建立

本文所建立的压电式换能器仿真模型是基于压电式换能器工作原理，以深圳市科美达超声波设备有限公司生产的KMD系列压电式换能器为设计蓝本，利用Comsol软件建立压电式换能器几何模型。KMD系列压电式换能器相关设计参数如表1所示。在Comsol软件中建立压电式换能器仿真模型及材料区域分布图，如图2所示。

表1 KMD系列压电式换能器相关参数Table 1 Relevant parameters of KMD piezoelectric transducer

1—固定钢钉； 2—钢钉座； 3—PZT-4 stack； 4—振动铝头； 5—水域层； 6—完美匹配层(PML)。图2 压电式换能器仿真模型及材料区域分布图Fig.2 Piezoelectric transducer simulation model and areal distribution of materials

本文选取6组工业中常用的超声波频率(20、25、28、40、80及120 kHz)分别进行研究，以探究超声波频率对油井套管清蜡效果的影响。

2.2 材料属性的定义及网格划分

在超声波油井套管清蜡应用领域中，常用的材料、声速如表2所示。

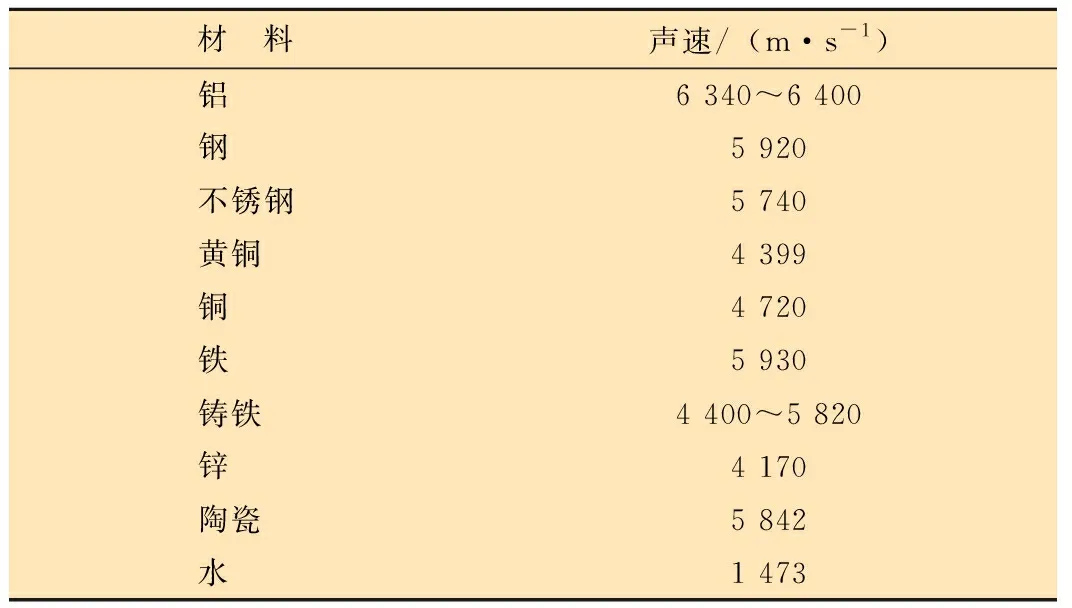
表2 材料声速表Table 2 Sonic velocity of materials

图2f所示的压电式换能器二维结构模型一共定义了4种材料：图2a表示的区域是压电式换能器固定钢钉和钢钉座，为钢结构域，材料属性定义为钢；图2b表示的区域是压电式换能器压电域，材料属性定义为PZT-4(软件内置压电材料)；图2c表示的区域是压电式换能器振动铝头，为铝结构域，材料属性定义为铝；图2d表示的区域是压电式换能器声波辐射区的水域，材料属性定义为标准状态的水。除此之外，为了模拟一个带有开放边界的域，该计算域的边界支持声波以无反射的方式通过，因此还需在图2e设置一个完美匹配层(PML域)，以探究声波在远场时所呈现的声学特性。

利用Comsol软件内置的网格划分功能对模型进行网格划分。为确保仿真模型的求解精度，需在邻近外场边界内的水域中创建一层边界层(见图3a)，以使模型内部的自由四面体网格与外部结构化网格单元之间产生平滑过渡，从而提升外场的计算精度。经设定，该仿真模型中完整网格包含317 706个域单元、23 617个边界单元和1 296个边单元。含计算网格的压电式换能器仿真模型几何结构如图3b所示。

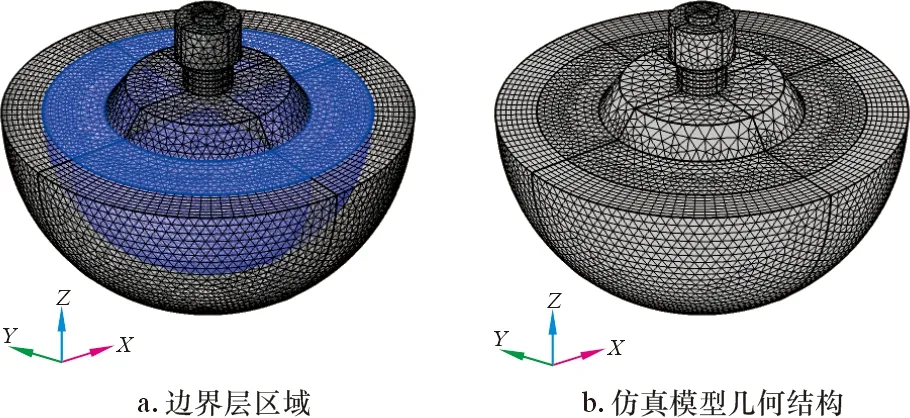
图3 压电式换能器仿真模型网格划分图Fig.3 Grid division of piezoelectric transducer simulation model

2.3 边界条件及仿真参数的设置

在利用Comsol和Matlab软件对超声波声场理论中所得结论进行仿真分析时，需首先对软件内相关物理参数进行配置。取水域半径为40 mm，完美匹配层厚度10 mm，额定驱动电压1 V，声波辐射角-90°～90°，声波频率为20、25、28、40、80及120 kHz。

针对1.3节所涉及到的相关参数，对取自大庆油田某8组作业区的原油样品进行测定，所测原油样品的物性参数及声学参数如表3所示。

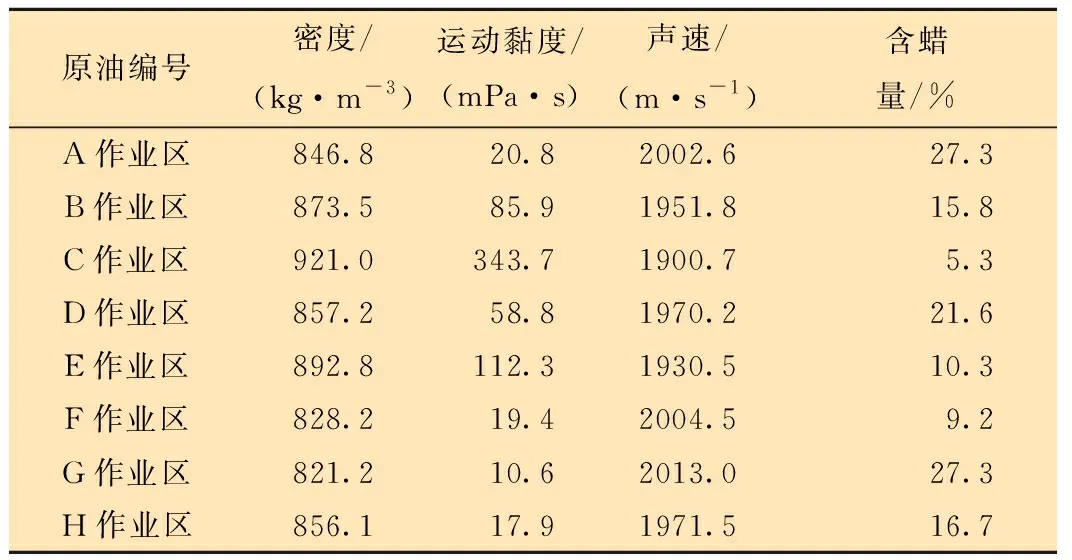
表3 原油样品相关物性参数与声学参数Table 3 Related physical and acoustic parameters of crude oil samples

3 结果分析

3.1 频率对超声波传播性的影响

选取压电式换能器模型的YZ平面为观测平面，观察不同超声波频率在内部声场(水域)及外部声场(PML域)所形成的声压辐射云图，结果如图4和图5所示。

由图4可知，在内部声场中，超声波的声压级峰值会随声波频率的增加而增加，但声压辐射场却随频率的增加而产生较大的扰动。根据式(8)可知，声压辐射场的扰动会对声波的声场指向性产生干预，进而对超声波的传播性造成影响。

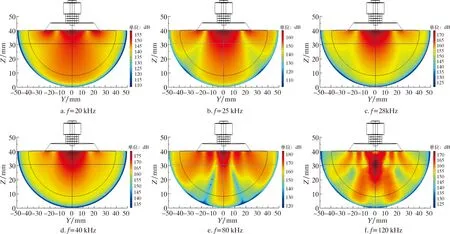
图4 6组待测超声波频率内部声场声压辐射云图Fig.4 Sound pressure radiation cloud chart of inside sound field at six ultrasonic frequencies

由图5可知，外部声场声压级分布范围随着声压辐射场的扰动而变化。为客观描述因频率变化所造成的声压辐射场扰动对超声波传播性的影响，在XY平面距坐标原点10 m处选取观测平面，绘制6组待测超声波频率在观测平面上相对0 dB的波束灵敏度极坐标图，如图6所示。

图5 6组待测超声波频率外部声场声压辐射云图Fig.5 Sound pressure radiation cloud chart of outside sound field at six ultrasonic frequencies

由图6可知，20、25及120 kHz的3组超声波频率在观测平面内声压级覆盖域较28、40及80 kHz的3组超声波频率声压级覆盖域小，所表征的声波传播性较弱。因此，在6组待测超声波频率中，频率为28、40及80 kHz的3组超声波传播性相对良好，可作为实现超声波能于油井套管(内径124 mm)内长距离清蜡作业的声波频率。

图6 6组待测超声波频率相对波束灵敏度极坐标图Fig.6 Polar diagram of relatively beam sensitivity at six ultrasonic frequencies

3.2 频率对超声波在非理想介质传播过程中声衰减的影响

针对3.1节所选取的3组超声波频率(28、40及80 kHz)根据第1章所得结论，还需讨论3组超声波频率由于声波辐射角度变化及传播介质黏度等因素的变化所造成的声衰减问题。

选取6组超声波频率为待研究量，声波辐射角度为自变量，将相关数据代入式(5)，通过Matlab软件绘制声波声强值随声波辐射角的变化曲线，如图7所示。

图7 声波声强值随声波辐射角的变化曲线Fig.7 Variation of sound intensity with sound radiation angle

由图7可知：当声波的辐射角θ∈(-90°,-20°)∪(20°,90°)时，各频率超声波的声强值较中心区域(θ=0°附近)有明显衰减，不利于清蜡；当声波辐射角θ∈(-20°,20°)时，超声波的整体声强值及声强值增加率随声波频率的增加而增加，且当声波辐射角θ=0°时，各频率超声波声强达到峰值。因此，将声波辐射角度θ∈(-20°,20°)定为声波最佳辐射角度范围。对比3组选定的超声波频率，在声波最佳辐射角度范围内，同一功率下单个换能器所产生的声强值在超声波频率为80 kHz时最大，40 kHz时次之，28 kHz时最小。

将相关数据代入式(10)，通过Matlab软件绘制出超声波在油井套管清蜡过程中声衰减系数与声波频率之间的关系，如图8所示。

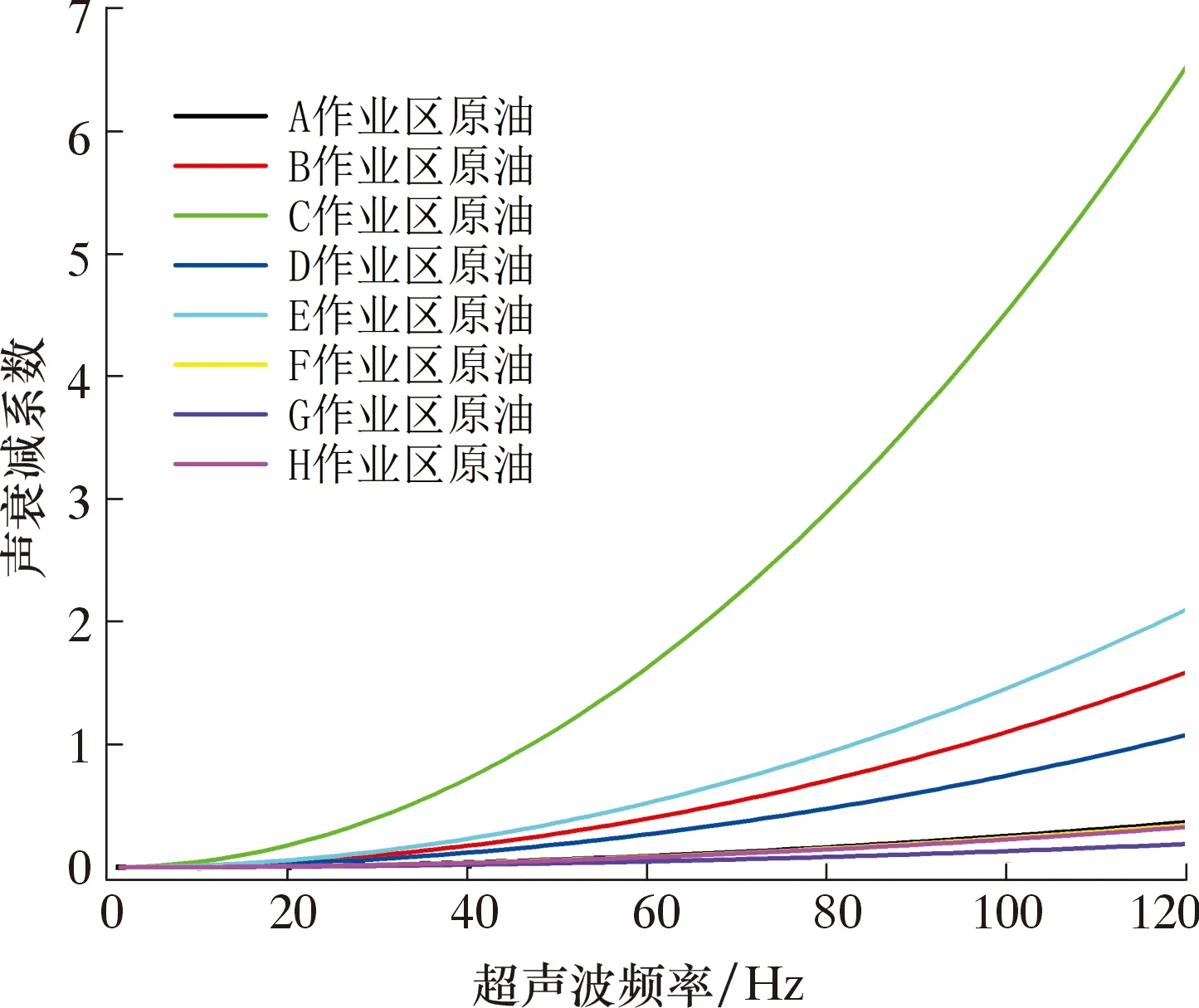
图8 油井套管清蜡过程中声衰减系数与超声波频率之间的关系曲线Fig.8 Relation between acoustic attenuation coefficient and ultrasonic frequency in wax removal process of oil well casing

由图8可知：在原油黏度为0～20.8 mPa·s的低黏度区间，原油介质对3组频率的超声波吸收不明显；在原油黏度为20.8～112.3 mPa·s的中等黏度区间，原油介质对频率为80 kHz的超声波吸收明显，对其余2组频率的超声波吸收较弱；在原油黏度不小于112.3 mPa·s的高黏度区间，原油介质对3组频率的超声波整体吸收明显，其中对频率为28 kHz的超声波吸收相对较弱。

基于以上分析结果，将上述3组超声波频率的相关特点、适用范围及适用工况绘制成清蜡作业超声波频率选择建议表，如表4所示。

表4 油井套管清蜡作业超声波频率选取建议表Table 4 Recommended ultrasonic frequencies for wax removal of oil well casing

4 结 论

(1)在6组待测超声波频率中，频率为28、40及80 kHz的3组超声波传播性相对良好，可作为实现超声波能于油井套管(内径124 mm)内长距离清蜡作业的声波频率。

(2)声波最佳辐射范围为-20°～20°，并且在此范围内，同一功率下单个换能器所产生的声强值在超声波频率为80 kHz时最大，40 kHz时次之，28 kHz时最小；原油黏度升高对频率为80 kHz的超声波声吸收最明显，40 kHz次之，28 kHz最弱。

(3)可通过油井套管清蜡作业超声波频率选取表选择超声波频率，以此提高油井清蜡作业效率。