火力发电厂锅炉智能融合故障诊断方法

马连彬

（中电建湖北电力建设有限公司，湖北武汉 430080）

0.引言

人们在日常生活和生产工作中离不开电力资源，而发电厂是为人们提供电力资源的重要保障，只有确保发电厂及厂内设备的稳定运行，才能够确保社会秩序的稳定及发展[1]。在当前形势下，锅炉仍然是火力发电厂中重要的设备，若在这一环节出现故障，则会对输出的电力质量产生极大的影响，不仅会影响到社会稳定运行，同时对于火力发电厂的自身利益也会造成影响。因此，当前火力发电厂将锅炉运行相关的安全问题放在了战略层面上，而有针对性地执行锅炉定期、不定期安检工作，不仅可以保证电厂锅炉在运行中的稳定性，同时也可以为火力发电厂的安全、持续化运行提供保障[2]。为实现对锅炉故障的有效处理，需要在设计方法前，对其常见的故障现象进行总结与描述，具体包括：锅炉灭火、锅炉受热面上管道爆裂、锅炉尾部烟道再燃、锅炉压力过高等。造成上述问题的原因包括：燃烧材料质量较差、通风量不足、材料检验未达标便应用到锅炉运行中、给水流量不合理等。由于锅炉故障的类型众多，并且对应的故障因素复杂，并且存在故障类型或故障因素同时存在的可能，因此对锅炉的故障诊断难度和复杂度进一步提升[3]。针对这一问题，应用现有故障诊断方法很难实现对其有效诊断，为了进一步提高火力发电厂锅炉的运行稳定性，本文开展火力发电厂锅炉智能融合故障诊断方法研究。

1.火力发电厂锅炉智能融合故障诊断方法设计

1.1 火力发电厂锅炉故障特征提取

在对火力发电厂锅炉的故障问题进行诊断时，需要获取锅炉在运行过程中产生的实时数据，因此在锅炉运行中在其周围设置多个测点，通过各个测点实现对锅炉运行电力信号和物理信号的采集[4]，根据各类信号信息能够实现对锅炉故障特征的有效提取。在锅炉运行过程中会产生数万个信号数据，通过对特征数据的选择，提高故障诊断的效率，并降低计算量。基于此，本文选用Relief算法从已知的火力发电厂锅炉数据当中随机挑出一组数据，并将其作为样本数据R。再从与样本数据R相同类别的数据当中，挑选出最近的相邻数据，并构成相邻数据样本H；从与样本数据R不相同类别的数据当中，挑选出最近的相邻数据，并构成邻数据样本M。最后，计算每个特征上样本数据R与M和H之间的距离[5]。根据距离实现对不同类别的区分。例如R与M之间的距离大，而与H之间的距离小，则说明该变量数据特征值高，反之同理，特征值低。在重复n次后，计算得出每一个变量的平均值，并以此实现对各个变量分类能力的表示。根据上述思路，利用Relief算法对每一个特征进行权重排序。在进行权重排序时，可将公式（1）作为依据：

公式（1）中，m表示为信号振荡频率；L表示为信号数据到样本数据R之间的距离；δ表示为信号容量；ρ表示为信号数据的模糊特征量。根据上述公式，计算得出各个样本数据集合中信号数据距离，并将符合公式（1）的数据提取，将其作为特征样本数据。在实际应用中，对锅炉的运行产生影响的特征数据包括锅炉主蒸汽温度、过热器温度、烟温、机组负荷等。

1.2 构建锅炉故障诊断模型及模型训练

在实现对火力发电厂锅炉故障特征提取后，由于锅炉故障问题分为多种不同类型，本文选择在构建诊断模型的过程中，引进SVM分类器，使用此分类器进行故障数据集合的训练与迭代处理。确保迭代数据的集成化与全面优化。在此基础上，将所选的分类器与核函数建立连接关系，对特征数据进行映射，将现有的单维度数据集合映射到高维度数据空间中，实现对数据边界的生成。将SVM定义为（w，b），其中w表示为权重量；b表示为权重偏差。将（w，b）中的最佳权重和最佳权重偏差定义为w0和b0。w与b之间存在下述关系：

公式（2）中，T表示为补偿系数；x表示为特征数据。利用通过上述特征提取后剩余的数据作为训练集合，将其导入到SVM分类器当中，以此实现对锅炉故障诊断模型的构建。为了进一步提高模型的诊断精度，将构建的模型带入到LVQ神经网络当中，并对其进行训练。通过自组织特征的改良，得到更智能的诊断模型。LVQ神经网络与其他训练网络相比，具备结构简单，计算方便等优势，同时通过各个层级之间的相互作用，对输入数据和对竞争层距离的计算，以此实现分类[6]。如图1所示为基于LVQ神经网络的模型训练流程示意图。

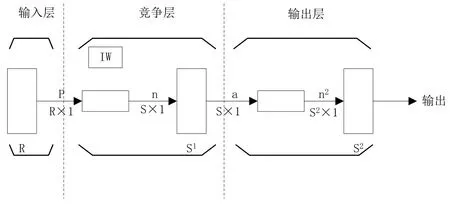
图1 基于LVQ神经网络的模型训练流程示意图

图1中S为分类器，在模型训练的过程中将LVQ神经网络层划分为3个层次。其中，中间层中所含有的原始变量数据最多。在此基础上，按照上述图1所示的内容，进行原始数据输入量之间距离的计算，选择距离较近的数据作为变量数据。若在计算过程中出现两种原型变量数据类别相同的情况，需要将计算结果进行靠近处理的方式解决。根据上述论述，对所有模型中的变量进行划分，并实现对模型的训练。

1.3 基于融合规则的故障诊断决策融合

在利用上述构建的模型得出锅炉的故障诊断结果后，为了确保模型结果的可靠性，针对多次输出结果，利用融合规则对其进行决策融合。假设模型对于故障诊断问题的全部依据可以由θ提供的若干证据进行归纳总结，其中θ即为融合规则，是针对锅炉故障问题域的有限n个互拆假设集。同时，利用融合规则给出多个依据的组合规则，将模型输出的不同结果通过规则进行分配，从而生成一个新的规则函数，其表达式为：

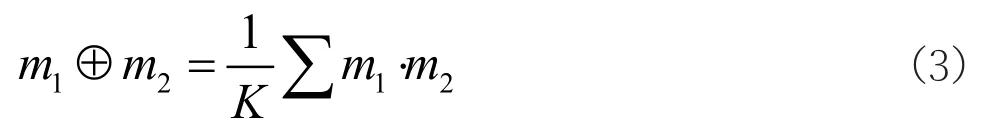
公式（3）中，m1和m2表示为通过诊断模型输出的不同诊断结果，K表示为归一化常数，⊕表示为决策融合。在实际应用中，按照上述公式将模型得出的锅炉故障诊断结果代入，通过规则函数对其进行决策融合将输出结果作为最终的诊断结果。

2.实例应用分析

为了进一步验证本文上述提出的故障诊断方法在实际应用中的可行性，选择以某火力发电厂作为依托，利用本文上述提出的诊断方法对该发电厂中现有锅炉进行故障诊断。提取该火力发电厂近5个月内的运行数据作为测试数据，已知在5个月内锅炉出现了几次不同的故障问题，并且相关信息记录在了测试数据内。为了确保最终应用效果的真实性，在测试过程中，确保故障诊断方法在应用中所处环境为火力发电厂锅炉正常的运行环境。分别从本文方法的故障诊断性能和决策融合性能两方面对方法的应用效果进行评价和验证。

2.1 本文方法故障诊断性能验证分析

首先，为了实现对本文方法故障诊断性能的验证，尝试引入混淆矩阵，利用该矩阵实现对本文方法故障诊断结果分类准确率的可视化展现。将上述获取到的测试数据作为研究对象，利用本文上述提出的诊断方法对锅炉故障问题进行诊断，并给出相应的故障类型，将其与实际锅炉的故障情况以及故障类型进行对比。如表1所示为本文故障诊断方法的混淆矩阵结果。

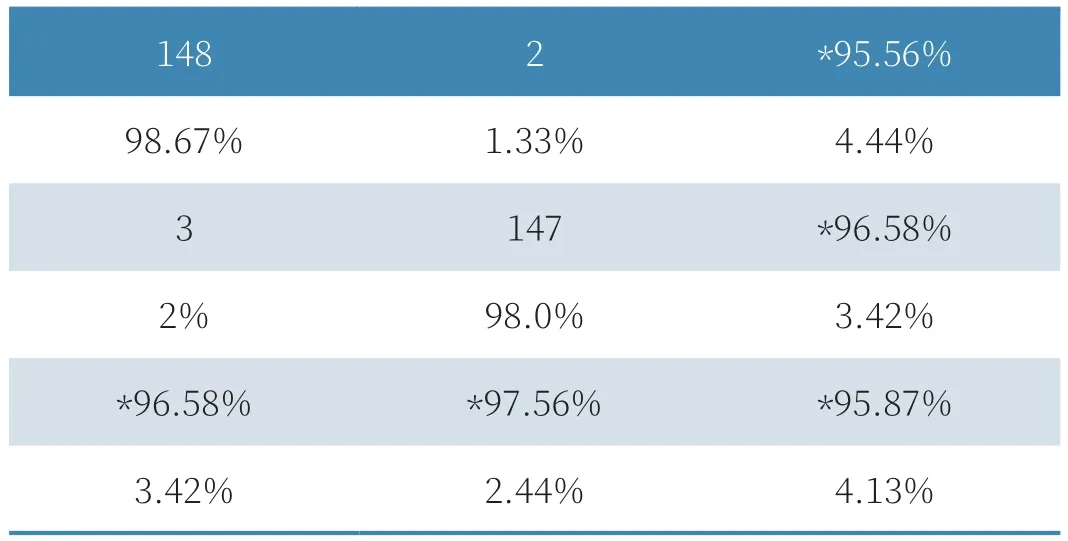
表1 本文故障诊断方法的混淆矩阵结果

表1中“148”“147”表示为在故障诊断过程中测试数据内共包含的正常运行锅炉数据；“3”“2”表示为在故障诊断过程中测试数据内包含的异常运行锅炉数据。表1中带有“＊”符号的数据为本文故障诊断方法正确诊断的概率。同时，在表1混淆矩阵当中，每一列的数据总数表示在该类别下对应的数据实际数目。通过上述混淆矩阵可以看出，将本文提出的故障诊断方法应用到对锅炉的故障诊断中，能够使最终结果的分类准确率达到95.00%以上。因此，通过上述得出的结果能够初步证明，本文提出的故障诊断方法能够实现对锅炉的高精度诊断，在实际应用中具有极高的应用价值，证明该方法可行。

2.2 本文方法决策融合性能验证分析

在明确本文故障诊断方法的应用可行性后，再对该方法在应用过程中的决策融合性进行验证。仍然选择将本文提出的故障诊断方法应用到真实的火力发电厂锅炉运行环境当中，并针对上述获取到的测试数据进行故障诊断。为了实现对诊断方法决策融合性能的验证，选择将2次针对相同测试数据的锅炉故障诊断结果进行决策融合，并通过对比融合后结果的误报和漏报情况，实现对其融合效果的验证。其中，误报可通过误报率表示，其计算公式为：

公式（4）中，δ表示为本文诊断方法误报率；m表示为测试数据当中包含的故障数据总数；m'表示为诊断结果中与真实故障数据不相符的总量。漏报情况可通过漏报率表示，其计算公式为：

公式（5）中，χ表示为本文诊断方法漏报率；m0表示为本文诊断方法诊断结果当中包含的测试数据，数据中包含了正确诊断数据和错误诊断数据。根据上述公式，计算得出本文诊断方法的误报率和漏报率，并将其记录如表2所示。

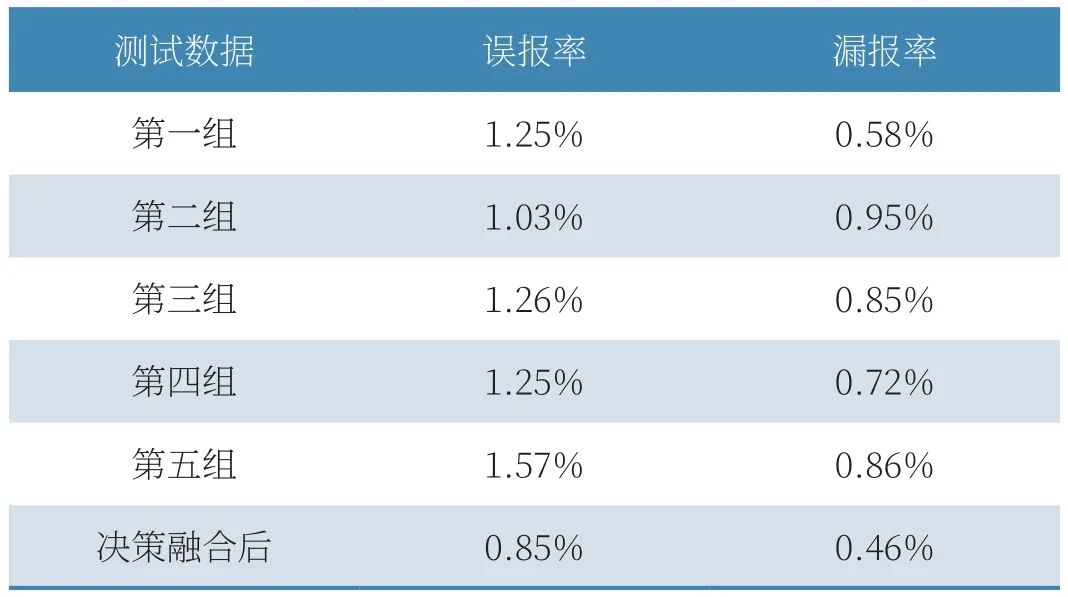
表2 本文故障诊断方法误报率和漏报率记录表

从表2中记录的数据得出，本文故障诊断方法在决策融合前，通过5次故障诊断，其诊断结果的误报率均在1.00%～1.50%范围内，而漏报率均超过0.50%。通过决策融合，误报率低于1.00%，漏报率也降低到了0.50%以下。由此可以看出，本文提出的故障诊断方法在完成诊断后，通过决策融合能够进一步降低诊断结果的误报率和漏报率，从而提高故障诊断方法的诊断精度。

3.结语

锅炉装置是火力发电厂中的核心设备，对于整个行业以及人们日常生活都有着十分重要的意义。通过本文上述论述研究，在明确锅炉运行特点以及常见的故障类型，以及故障发生原因的基础上提出一种全新的故障诊断方法，同时也通过应用实现了对其各项性能的检验。在实际火力发电厂运行中，除了应用本文提出的故障诊断方法为锅炉运行和维护提供重要依据外，还应当从根本上提高对锅炉安全检验的重视程度，确保锅炉在运行中的质量和效率，促进火力发电厂能够更快适应当前社会发展趋势。