基于多元变模式分解的机械设备故障诊断方法

方学宠，苏立鹏，尤戈，李拥军

(温州市特种设备检测科学研究院， 浙江温州 325000)

0 前言

随着国家一系列经济政策的推进，高端制造业在国民经济中发挥着越来越重要的作用。高端制造系统和先进机械设备作为高端制造业发展的前提，是推动我国制造业由传统向智能升级的关键力量。高可靠性、高精度、高智能化的先进机械设备是高端制造的最基本条件。轴承、齿轮等部件作为旋转机械的重要组成部分，在实际作业中不可避免地会产生故障。机械设备发生故障时，不仅会造成大量的经济损失，甚至造成严重的人员伤亡。因此，对机械设备的运行状态进行监测和诊断具有重要的经济意义和社会意义。

机械设备的故障信号往往伴随着非线性、非平稳等特点，且信号微弱、调制性强、背景噪声大。采用振动传感器采集到的信号往往是有用故障特征信号和无用噪声信号的叠加，故需要对故障特征信号进行提取。在机械设备故障诊断方面，冯平兴和张洪波提出了一种基于特征矩阵联合相似对角化及经验模态分解(Joint Approximative Diagonalization of Eigen matrix-Empirical Mode Decomposition，JADE-EMD)的多故障动态盲分析技术，用于滚动轴承的故障诊断。但EMD分解缺乏严格的数学基础，容易产生模态混叠、端点效应。辜志强和林月叠将改进的局部均值分解(Local Mean Decomposition，LMD)和综合特征指标结合起来，用来对滚动轴承进行故障诊断。但LMD分解存在着迭代计算量大、由解调引起的信号突变等问题。变分模式分解(Variational Mode Decomposition，VMD)是一种新的时频分析方法，具有较好的抗噪性和更高的频域分辨力，能够提取出较微弱的信号成分。然而VMD分解必须提前设定分解层数，层数设置不当会引起模态混叠或者大量虚假分量的产生。多元变模式分解(Multivariate Variational Mode Decomposition，MVMD)由REHMAN 和 AFTAB在2019年提出，通过建立约束变分模型表达式，将信号以非递归的方式自适应分解。MVMD算法将VMD算法从单通道拓展到多通道，可以同时处理多通道数据，既避免了频率不匹配问题，又解决了多元经验模式分解(Multivariate Empirical Mode Decomposition,MEMD)的模式混叠问题。

综上，本文作者提出一种基于MVMD的机械设备故障诊断方法。采用3个单向传感器采集机械设备故障综合实验台的振动信号；对采集到的振动信号进行MVMD分解，获取能够表征故障特征的一系列IMF分量，并与MEMD的分解结果进行对比。结果表明：所提出的MVMD算法是诊断和分析机械设备多元故障信号的可靠手段。

1 理论描述

1.1 变分模式分解

VMD的目标是将输入数据()分解为个预定义的本征主模()，即：

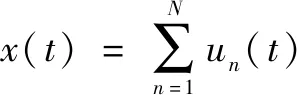
(1)

(2)通过具有频率的复指数的谐波混合信号将得到的单边频谱移至基带；

(3)取上一步中获得的谐波混合信号的梯度的平方范数。因此，相关的约束变分优化问题变为

(2)

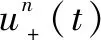
构造一个增强的拉格朗日函数：

(3)

其中:()为确保严格满足约束条件的拉格朗日乘数。

频域上()与的迭代公式为

(4)

式(4)将新频率估计为相关模式功率谱的重心，给出的频谱域中的模式和中心频率迭代关系构成了VMD算法的关键。

1.2 多元变分模式分解

作为VMD算法用于多维空间中的多维数据的广义扩展，MVMD从包含个数据通道的输入数据()=[(),(),…,()]中提取预定义的个多元调制振荡()，即：

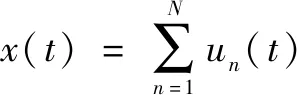
(5)

其中:

()=[(),(),…,()]

(6)

式(6)中有多个线性相等约束对应于通道总数。相应增强的拉格朗日函数变为

(7)

如式(4)所示，VMD的模式迭代在傅里叶域中得到解决，从而在频域中产生了简单的迭代关系，MVMD模式迭代的最小化问题的等效优化如下：

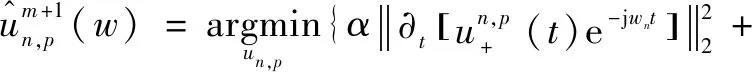
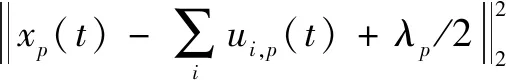
(8)

MVMD的模式()的迭代关系为

(9)

考虑到式(7)拉格朗日函数的后两项不依赖于，对于中心频率的迭代的优化问题简化为

(10)

为了在频域中更方便地执行优化，使用在时间和频率域中关联函数内积的Plancherel定理，将上式转化为

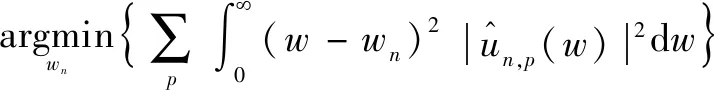
(11)

最小化上述二次函数之和，得到以下中心频率的迭代公式：

(12)

2 数值仿真分析

为验证所提方法的可行性，首先进行数值分析。滚动轴承是支撑机械设备旋转部件的重要传动部件,如果轴承的外圈固定在轴承座上，典型的内圈故障模型可以简化如下：

()=sin(2π)[1+sin(2π)]

(13)

式中:为内圈故障频率；为转频。

采用以下3个源信号来模拟采集到的振动信号：

()=02cos(2π+10)

(14)

()=03sin(2π-15)

(15)

()=04sin(2π)[1+sin(2π)]

(16)

其中:3个模拟信号的特征频率分别为=20 Hz、=50 Hz；=100 Hz；=15 Hz。采样点数和采样频率分别为=1 024、=1 024 Hz。

在传感器采集信号的模拟过程中，任意一个传感器同时采集振动信号，三元信号是由上述3个模拟信号组成的瞬时混合信号。鉴于采集到的振动信号伴随着噪声，将方差为0.5的高斯白噪声加到观测信号中，用表示。选择3×3的随机矩阵将模拟源信号混合在一起，其表达式如下：

(17)

然后，瞬时混合信号模型可以描述为=+,={,,}，它表示由3个传感器使用的3个源信号产生的带有噪声的三元信号。图1和图2所示分别为FFT计算得到的三元信号的时域和频谱分析结果。

图1 含噪声的混合三元信号的时域图

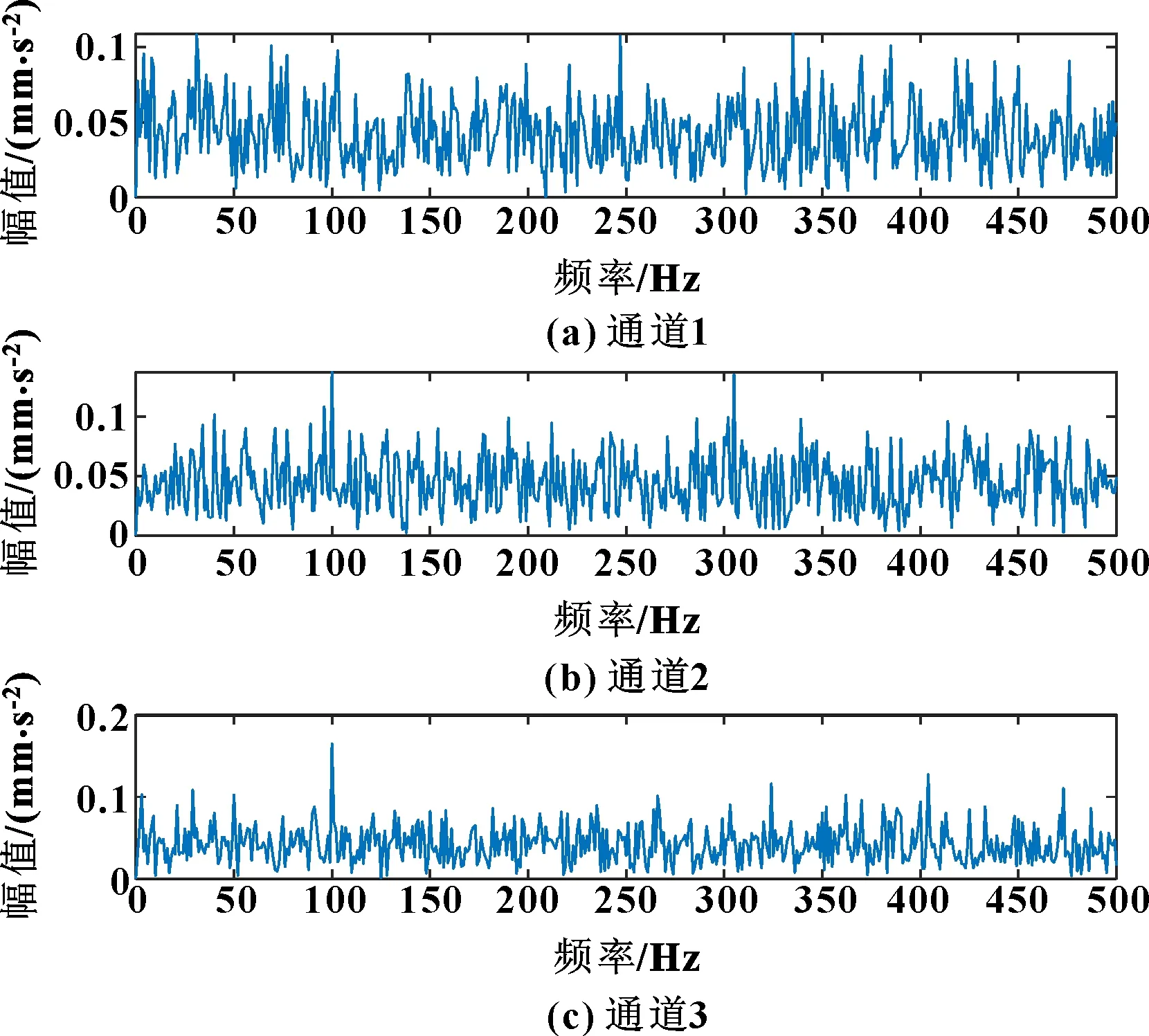
图2 带噪声的混合三元信号的频谱

由图1和图2可以看出：在含有噪声的情况下，很难识别观测到三元信号的频率特性和调制现象，只能在第3个通道识别出内圈故障频率，其他频率分量对所有通道都不明显。这说明噪声的影响不容忽视，需要采用更先进的方法进行处理。

采用传统的MEMD方法对仿真信号进行处理，结果如图3所示。可以看出：MEMD在保证分解结果的稳定性方面具有优势。然而，特征频率、和调频±仍然无法识别。

图3 MEMD方法的处理结果(频谱)

应用MVMD对三元信号进行处理，结果如图4所示。为阐明去噪性能，根据与原始信号的最大相似度选择IMF3、IMF4和IMF7分量进行频率分析，结果如图5所示。可知：在IMF3中可以找到调频±；特征频率、也可以分别在IMF4和IMF7中看到。仿真结果表明，MVMD在信号分解方面具有较高的可靠性。

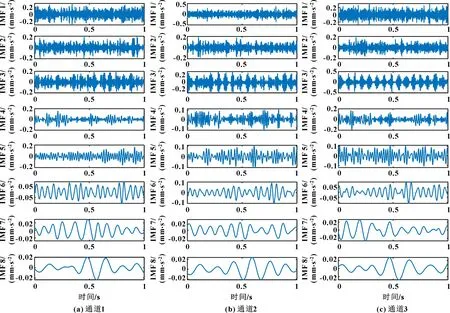
图4 MVMD方法的处理结果(时域)

图5 MVMD方法中不同信号的IMF3、IMF4、IMF7分量结果

3 实验研究

为进一步验证所提出方法的有效性，利用机械设备故障综合实验台对获取的振动信号进行分析。实验台实物如图6所示，主要由电机、调速器、齿轮箱、轴、轴承等组成。文中所用到的故障轴承为滚动轴承(型号NJ2232WB)，故障类型为外圈故障，如图7所示。滚动轴承的结构参数如表1所示。3个加速度传感器分别安装在轴承座的水平(H)、垂直(V)、轴向(A)3个方向上，测量3个方向上的振动信号，旋转频率=8.5 Hz，信号的采样频率为20 kHz，按照下面理论公式(18)—(20)计算得到的外圈故障频率为=60.1 Hz，内圈故障频率为=81.6 Hz，其故障特征参数如表2所示。

图6 旋转机械振动故障诊断实验台 图7 轴承外圈故障实物图

表1 滚动轴承NJ2232WB结构参数

表2 滚动轴承特征频率 单位:Hz

(18)

(19)

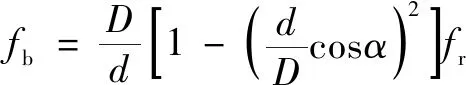
(20)

图8(a)(b)(c)是3个单向传感器采集到的振动信号的时域波形图，可以看出原始信号中含有明显的冲击和噪声。3个单向传感器采集得到振动信号的频谱分析结果分别如图8(d)(e)(f)所示。可以发现，旋转频率及其倍频、外圈或者内圈故障频率及其倍频都无法识别。

图8 原始振动信号时域图和频谱图

使用常用的多元模式分解算法MEMD和文中提出的MVMD算法对实验故障轴承三通道振动数据进行分解，其中MEMD分解得到12个模式分量，MVMD分解得到9个模式分量。为了便于显示，选取前面的6个模式分量，分别如图9和图10所示。通过计算得到IMF3为包含特征信息的有用分量，对它进行傅里叶变换，从而寻找频谱中的故障特征。图11所示为MEMD对3个单通道传感器信号降噪后的频谱分析结果。可知:由于噪声和无关信号成分的干扰，第1个通道无法识别出故障特征频率信息，在第2个通道中可以发现外圈故障频率及二倍频2，在第3个通道中可以找到和3。图12所示为利用MVMD进行多元模式分解的结果。可以看出：在每一个通道中，外圈故障频率及其倍频(2、3)均可以被准确地识别。另外，噪声部分已经被去除，信号的信噪比得到了提高。实验结果表明，所提出的分解方法可较准确地提取滚动轴承故障特征频率。

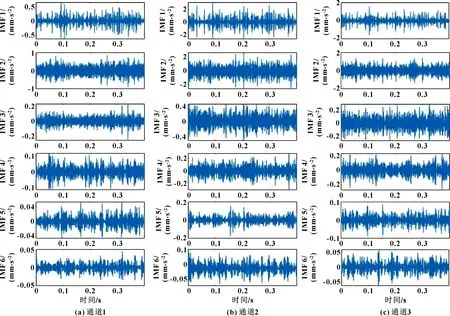
图9 MEMD分解结果

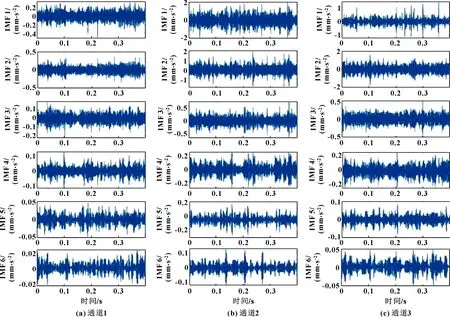
图10 MVMD分解的结果

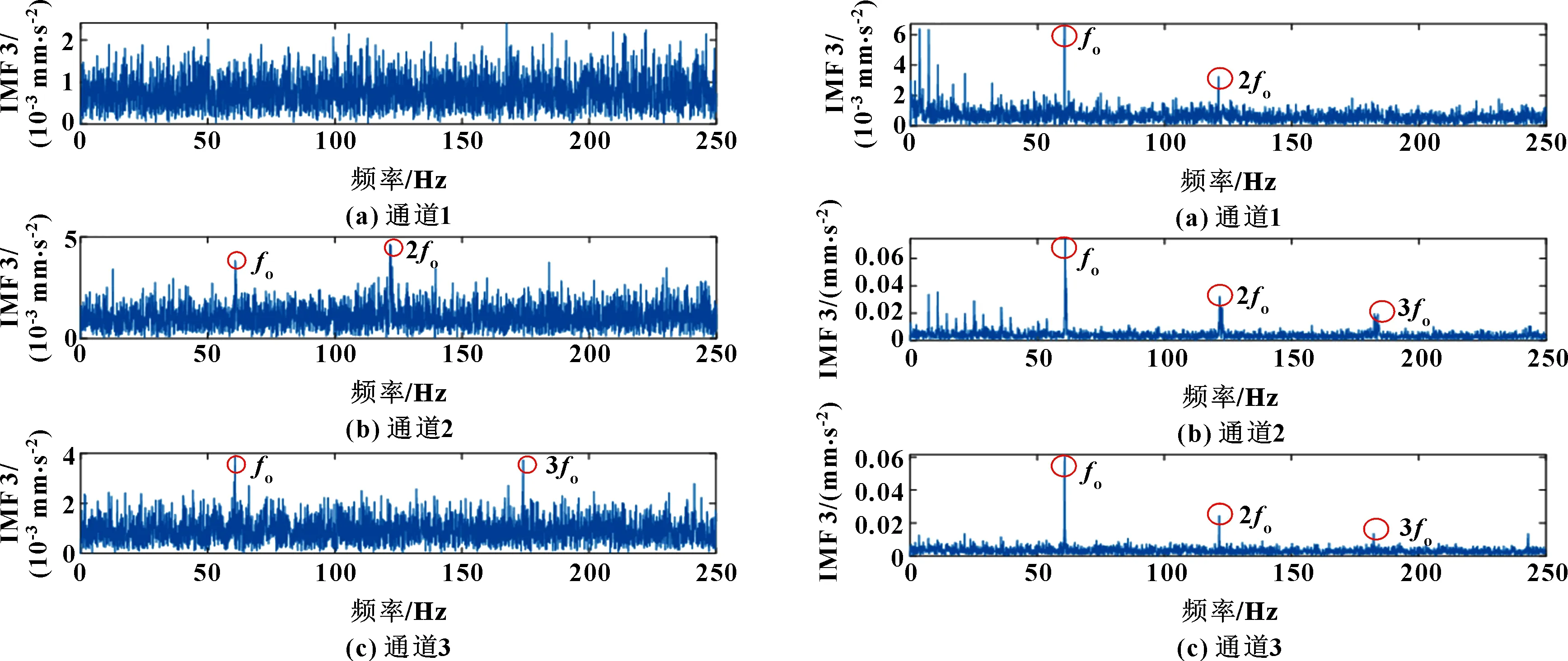
图11 MEMD 对3个传感器振动信号降噪处理的结果 图12 所提出的MVMD对3个传感器振动信号降噪处理的结果

4 结论

针对现有时频分析方法对含有强噪声成分和强调制成分的机械设备振动信号的特征提取性能较差的问题，本文作者提出一种基于多元变模式分解的机械设备故障诊断方法。该方法不仅可以同时处理多通道数据，而且还能有效避免传统时频分析方法存在的模态混叠问题，能够将多通道振动信号自适应地分解成多个具有物理意义的模式分量。将所提方法运用到多传感器采集的轴承故障信号中，实现了对多通道信号的降噪和故障特征提取，验证了所提方法的可靠性。