基于自适应的NSGA-Ⅱ多目标柔性作业车间调度

王冠，高尚，房思佳

(1.河北科技大学经济管理学院，河北石家庄 050018；2.上海集成电路装备材料产业创新中心有限公司，上海201800)

0 前言

柔性作业车间调度是典型的NP-hard问题需要兼顾生产设备分配和工序排列方案，与传统车间调度相比更加贴近真实情况。在实际应用中，仅围绕单一目标进行评价愈发难以满足实际需求，因此将研究重点聚焦在多目标柔性车间调度上。有许多算法可用于求解此类问题，例如遗传算法、粒子群算法、蚁群算法、免疫算法等。遗传算法因具备收敛性好、鲁棒性高且有较好的扩展性等优点得到了更多的青睐。其中，吴秀丽等提出了一种混合遗传算法；鞠全勇和朱剑英将粒子群和遗传算法的优点相结合，提出了多种群混合遗传算法。非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm,NSGA)是由SRINIVAS和DEB提出，通过寻找Pareto最优解解决多目标优化问题的方法，虽然该方法可以推广到更高维、更复杂的问题，但是NSGA存在计算复杂度较高、没有精英策略的问题。其后，DEB等对NSGA进行改进，提出基于非支配排序的多目标遗传算法(NSGA-Ⅱ),以便在问题中找到更好的扩散解，实现了对这类问题更好的求解能力。

标准的NSGA-Ⅱ算法存在“易早熟”和易陷入局部最优的缺陷，所以研究柔性作业车间调度时需要对算法进行合理的改进。算法的改进主要针对交叉方法、自适应方法和寻找最优解等方面。在交叉方法的改进方面，张超勇等、宋昌兴等分别提出了基于工序编码的POX交叉算子方法和基于机器编码的MPX交叉方法，提高了精英库中的个体质量。在自适应方法改进方面，荆巍巍等在迭代过程的不同阶段动态调整交叉与变异的概率提高算法计算效率。YUAN等运用层次分析法确定多目标最优解的方式，改进了寻找最优解的方法。

综上所述，以最大完工时间、加工能耗、设备总负荷和最大延期时间4个方面为目标函数并建立数学模型，同时采用IPOX和改进的MPX方法分别实现工序层和设备层的交叉方案，应用了更高效率的具有自适应性的交叉和变异概率算法。在寻找最优解的过程中，先对Pareto解集中的各目标函数值进行量纲一化处理并运用层次分析法确定各目标权重，最终通过线性加权获得柔性作业车间调度方案的满意解。

1 多目标柔性车间调度模型

作为企业生产管理过程中的重要参考指标，文中根据完工时间、加工能耗、设备总负荷和延期时间4个方面建立目标函数并在满足多目标柔性作业车间工艺约束前提下，综合考虑多方面因素建立约束条件。

1.1 问题描述

在柔性车间生产单元最大荷载能力的限制下，待加工工件个数用表示，设备台数用表示，={,,…,}表示工件集合，={,,…,,…,}表示设备集合。工件(=1,2,…,)共包含(=1,2,…,)道工序，各工件的工艺流程已知，设备集中所包含的设备可满足所有工序的加工要求。表示第个工件的第道工序。因为每台设备的性能参数及型号不同，所以工序的加工时间、负荷和能耗会因为设备选择方案的不同而有所差异，最佳的设备选择与加工顺序方案直接构成最优的调度方案。

1.2 目标函数

表示从首个工件开始加工到最后工件加工结束所用时间，即最大完工时间。表示工件的完工时间，目标函数表示为

=min (max {|=1,2,…,})

(1)

表示所有工件在各道工序加工时所使用设备的能耗总和。表示设备加工第个工件第道工序的加工能耗，表示选择加工设备进行工序的加工，表示加工设备的待机消耗，目标函数表示为

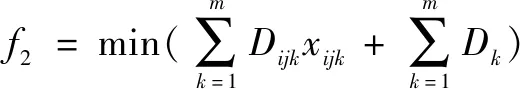
(2)

表示所有工件在各道工序加工时所使用设备的总负载。表示加工设备的最大载荷量，即在单位时间内加工设备完成的最大加工数量，目标函数表示为

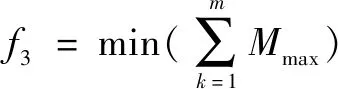
(3)

表示各工件延期交货时间总和。表示工件的交货期，目标函数表示为

=min(max|-|)

(4)

1.3 约束条件

文中做出如下假设：

(1)同工件存在工序约束，不同工件间不存在约束。

(2)每个工件的加工时间及加工情况已知，加工时间中已包括加工准备等其余必要时间。

(3)所有设备在=0时均为空闲状态。

表示工件第道工序在所选设备上开始加工的时间，表示工件第道工序在所选设备上完成加工的时间，工序间的约束表示为

≤(+1)

(5)

表示设备开始进行工序的加工时间，表示设备已完成工序的时间，表示工序在设备上的加工时间，工件加工一旦开始，中间不可中断，设备约束表示为

-=

(6)

工序在设备上的决策变量表示为

(7)

最大完工时间、加工能耗和加工设备总负载的函数值大于零且最小值最优，适应度函数表示为

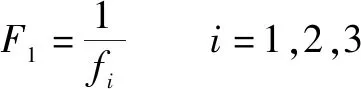
(8)

最大延期时间的函数值大于等于零且最小值最优，适应度函数表示为

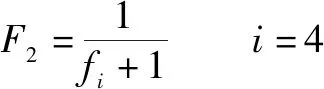
(9)

2 改进的NSGA-Ⅱ多目标柔性车间算法设计

解决多目标优化问题对算法性能有一定的要求，NSGA-Ⅱ因为具备计算效率高、收敛性好、鲁棒性强等优点成为较好的选择，但是其算法效率可以进一步提升。文中对自适应和交叉变异方案进行了改进，改进后的算法在运算过程中采用混合交叉和变异方案，并且在不同阶段动态调整交叉和变异概率。算法流程如图1所示。

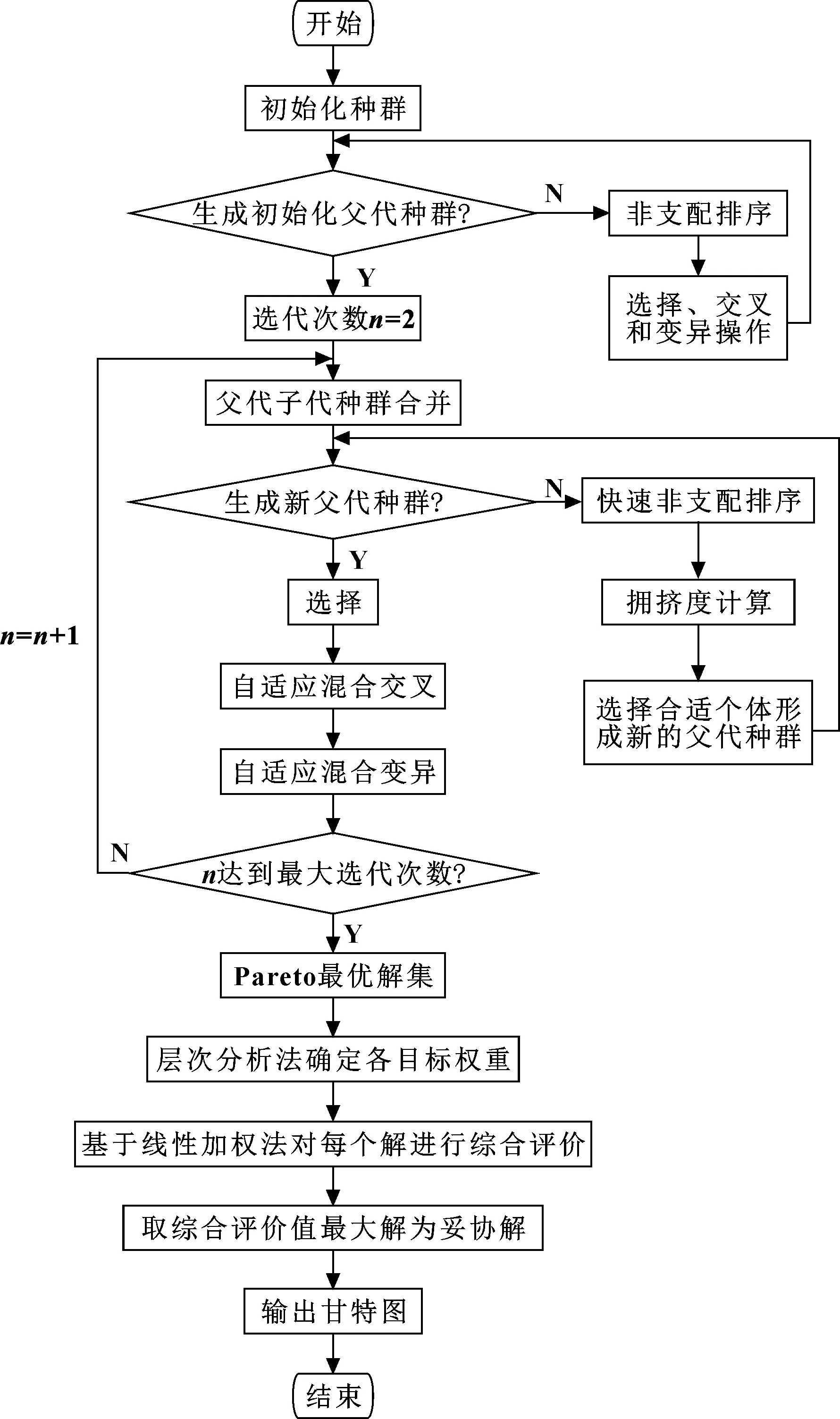
图1 改进的NSGA-Ⅱ多目标柔性车间算法流程

2.1 染色体编码与解码的设计

文中采用工序、设备双层编码的方式分别用于解决工序排列及设备分配问题。为了方便理解算法过程，以一个五台设备加工4种工件的柔性作业车间调度问题为例进行分析，工件1和工件3有3道工序，工件2和工件4有2道工序，各工件每道工序对应的可选设备集为5台设备中部分设备。基于工序、设备的双层编码过程如图2所示，工件号是工序编码方格内的数字，可选设备集表示第个工件在第道工序加工时可选用的设备集合，设备编码方格内的数字代表第个工件在第道工序加工时选用的设备序号。解码方式采用插入式贪婪解码，将个体编码转变成调度甘特图。

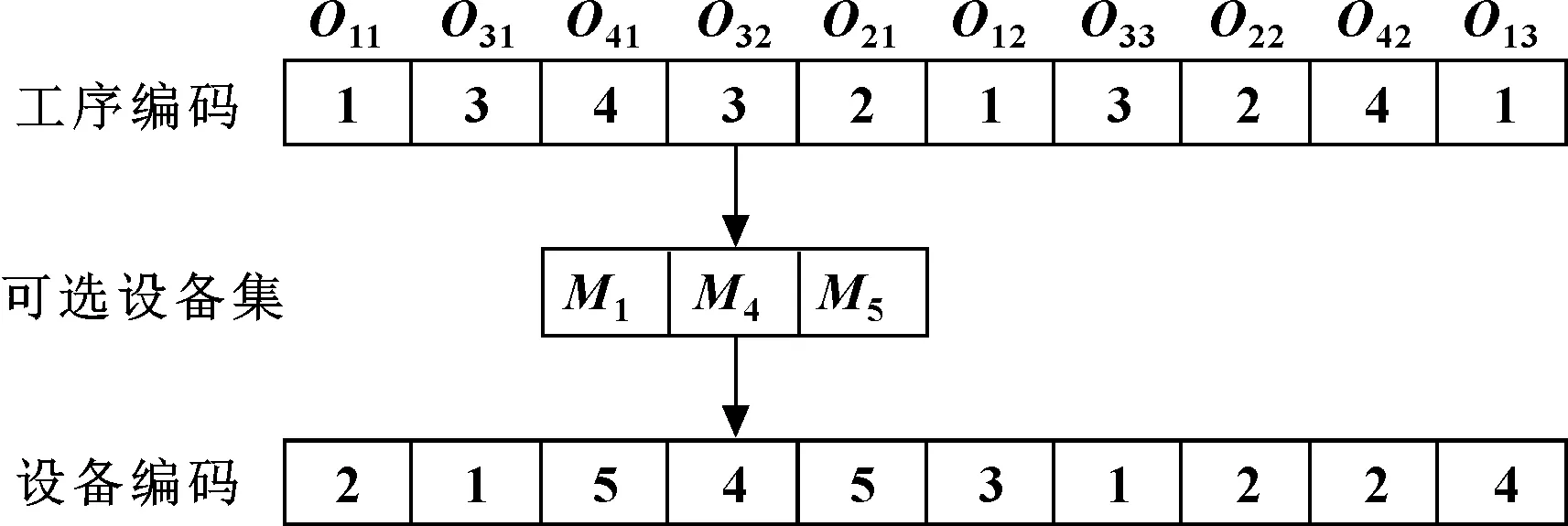
图2 基于工序、设备的双编码过程

2.2 选择操作

多目标优化问题中的各目标之间往往会相互冲突。为尽量避免此情况，文中采用快速非支配排序方法，从而有效地降低计算过程的复杂程度并寻出满意解。首先，对种群进行非支配排序，令种群划分为不同层级，接下来对同一层级内的个体进行拥挤度计算，最终应用二元锦标赛机制从种群中选出优先度较高的个体。优先度较高的个体选择原则为首先进行层级的比较，个体的层级越低越会被优先选择，其次比较拥挤度距离，个体的拥挤度距离越大越会被优先选择。其中，拥挤度距离计算方法如下：

(10)

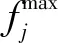
2.3 交叉与变异

2.3.1 混合交叉方案

基于IPOX交叉算子对工序进行交叉的流程如图3所示。首先从工件集中随机选取若干工件，如选取{,}，将PF1中的和工件按照相同的位置复制到PC1，将PF2中和工件按照相同的位置复制到PC2，将PF1中的和工件按照相同的顺序复制到PC2，将PF2中的和工件按照相同的顺序复制到PC1。因编码方式为工序与设备双层编码，所以在进行工序交叉时，当前父代所对应的设备也要进行与工序交叉相同的操作，操作流程如图4所示。

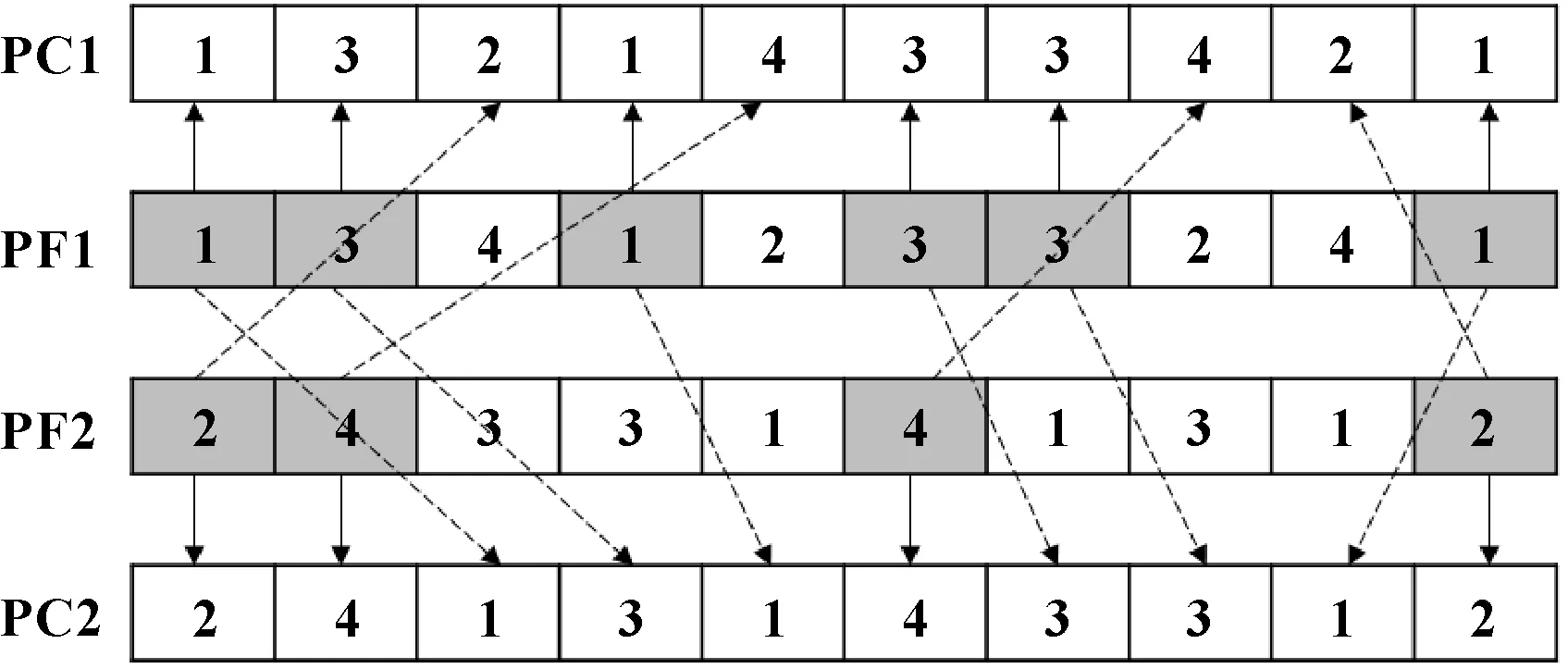
图3 IPOX工序交叉示意

图4 IPOX设备交叉示意

设备编码部分采用改进的MPX交叉，改进的MPX交叉流程如图5所示。首先从工件集中随机选取若干个工件，如选取{,}并记录它出现的位置，然后分别将父代设备编码MF1与MF2中非记录位置基因放入子代设备编码MC1和MC2，最后交换MF1和MF2中记录位置的相同工序设备基因，并依次插入子代对应位置。

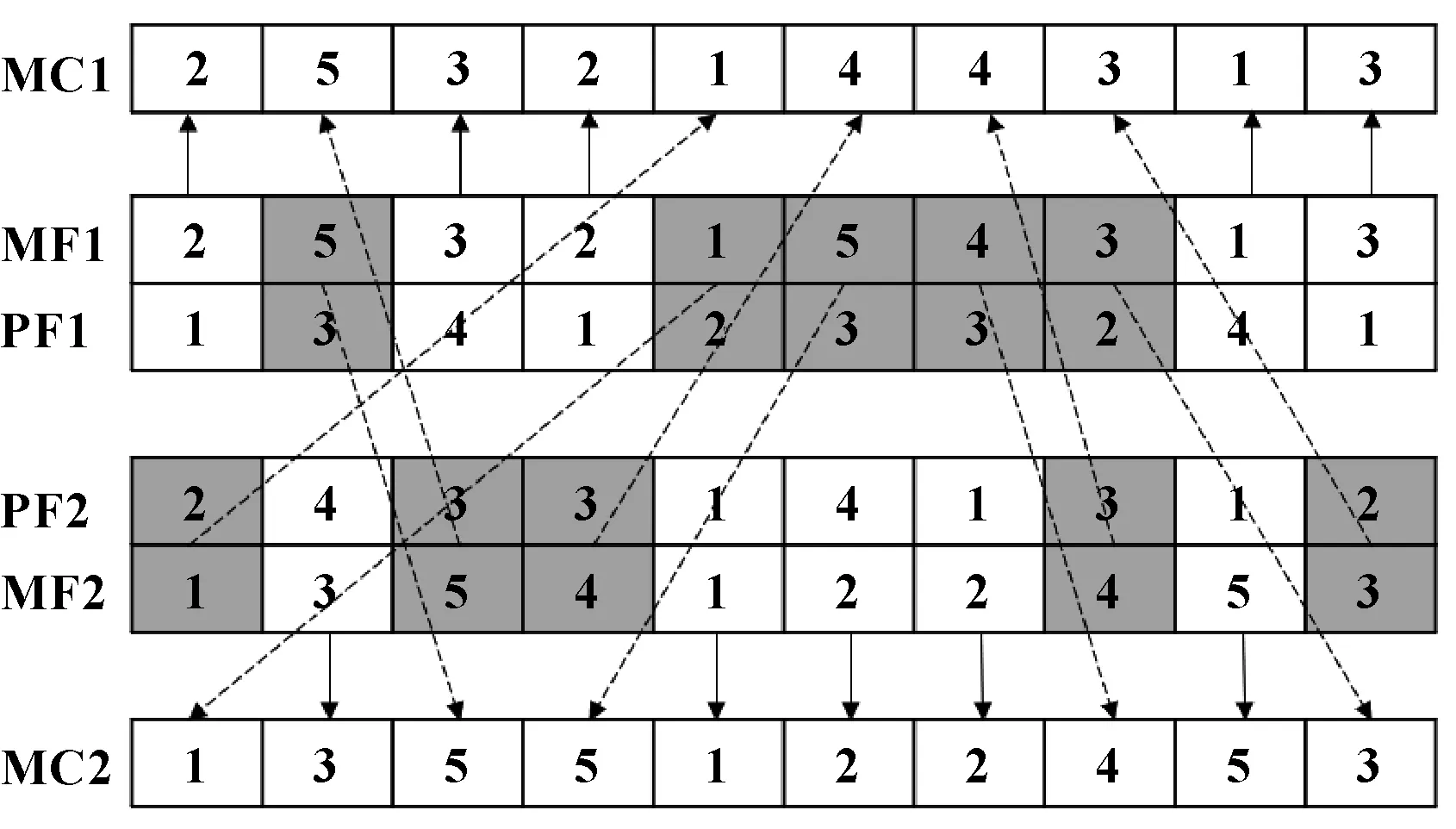
图5 改进的MPX交叉示意

2.3.2 混合变异方案

工序变异部分流程如图6所示。首先任意交换2道工序的排序，交换后按照每个工件的工艺顺序进行检验，发现因交换工序所产生的非法基因则对它进行修复。

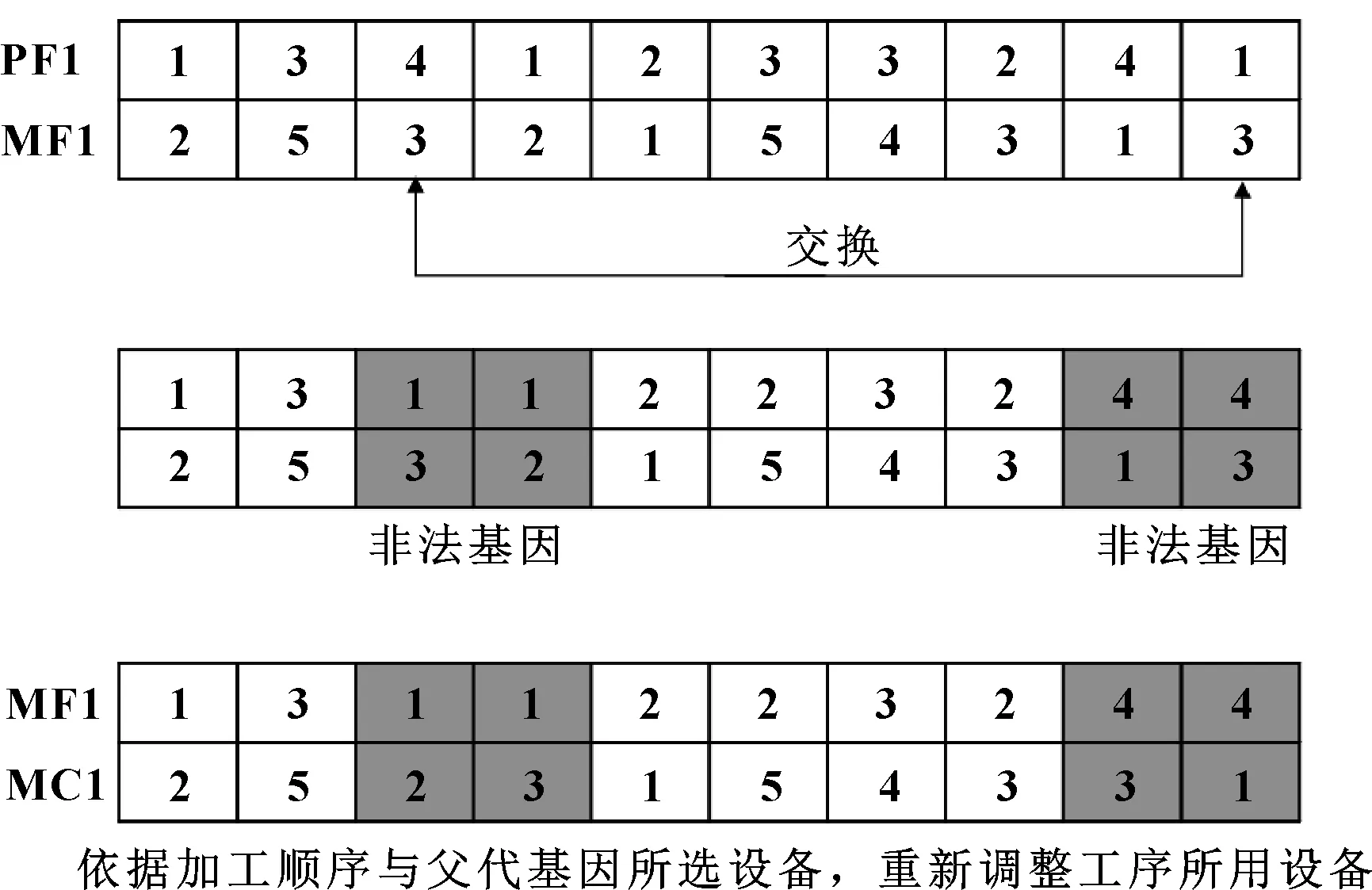
图6 工序变异示意

设备变异过程的示意如图7所示。首先任意选出一道工序，然后读取所选工序的可用设备集，并从设备集中任意选择一台设备替换当前设备，最后重新计算与其相对应的目标函数值。

图7 设备变异示意

2.3.3 自适应交叉、变异概率

交叉和变异概率对种群多样性和算法收敛有着重要作用。因为对参数设定不合理则会出现算法早熟、计算效率降低等问题，为防止上述情况发生，文中采用自适应交叉和变异概率，依据算法的迭代次数动态地更新交叉和变异概率，交叉概率和变异概率的计算方法如下:

(11)

首先由各个目标函数的适应度分量计算出交叉概率c和变异概率m，再取c和m的平均值得出交叉概率与变异概率，式中为目标函数的数量。max、avg和min分别表示种群中第个目标函数适应度的最大值、平均值和最小值;′为2个即将交叉个体中适应度较大值;为待变异个体的适应度值;1>>>>0，1>>>>0。

3 实例仿真

某石油企业的机加车间在调度周期内安排8台设备加工8种类型工件。柔性车间调度问题实例数据见表1，表中展示了不同类型工件的不同工序对应的可选设备集及加工时间。

表1 8×8柔性车间调度实例数据

文中以表1中数据为例进行MATLAB软件仿真分析，算法中各参数设定见表2。

表2 算法参数设定

计算过程中，各目标变化趋势如图8所示，图中所示为4个目标函数的平均值与标准差。依据图中的变化趋势可知各目标在经过60次迭代后趋于稳定。

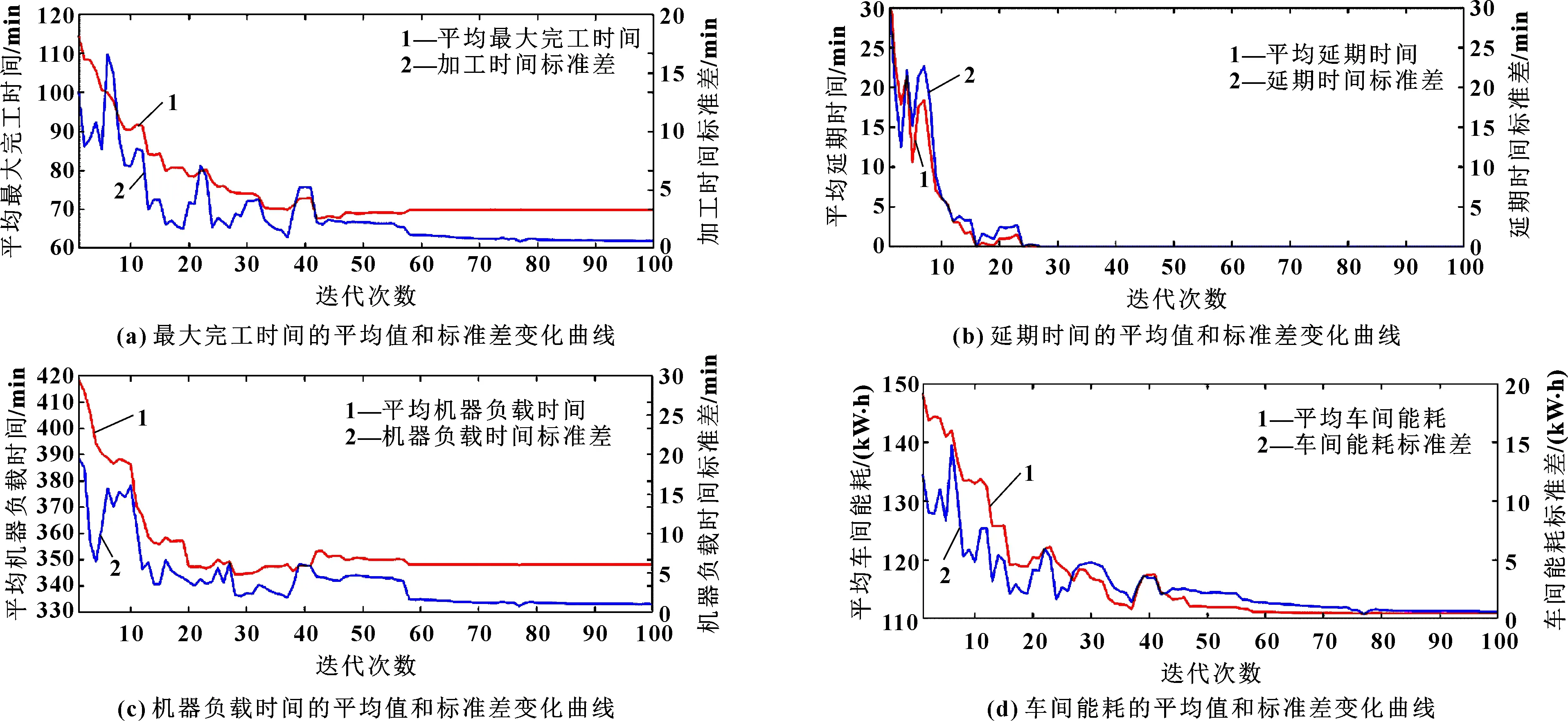
图8 迭代过程中目标函数变化趋势

在达到算法设置最大迭代次数后，对最终的Pareto解集采用线性加权法确定最满意解。需对目标函数值量纲一化进行比较，量纲一化方法如下:

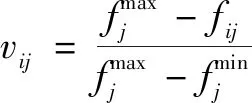
(12)

式中：=1，2，…，；=1，2，…，；和分别为Pareto解集中解和目标函数的数量;max和min分别为Pareto解集中第个目标函数的最大值与最小值，为量纲一化前的函数值，为量纲一化后的函数值。

通过线性加权的方法对Pareto解集中的所有解进行综合评价，若某解为解集中评价值最大的解，则选取它为满意解，计算方法如下:

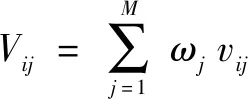
(13)

式中：表示赋予不同目标函数的权重大小；文中根据车间具体需求运用层次分析法得出最大完工时间权重为=0.35，最大延期时间权重=0.32，能耗权重=0.16，设备总负载权重=0.17。最终得到的最优调度甘特图如图9所示，最大完工时间为70 min，延期时间为0 min，设备负载时间为348 min，能耗为110.73 kW·h。

图9 最优调度甘特图

原始调度甘特图如图10所示，其最大完工时间为90 min，延期时间为10 min，机器负载时间为358 min，能耗为131.48 kW·h。对比图9、图10所示的方案可以发现:优化后调度方案的最大完工时间、加工设备负载时间和加工能耗相较于初始值分别减少了22.22%、2.79%和15.78%，延期时间减少了10 min。

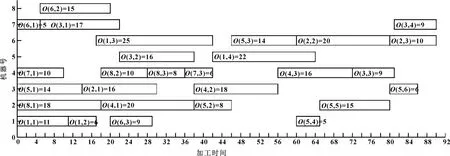
图10 原始调度甘特图

4 结论

文中考虑到算法运算的不同迭代次数对交叉和变异概率的要求不同，提出了交叉和变异概率在算法不同阶段动态改变的自适应NSGA-Ⅱ算法，然后采用能够显著提升NSGA-Ⅱ算法计算效率与精度的IPOX和改进的MPX对工序层和设备层进行交叉操作，在提高种群多样性、避免非法解产生的同时有效提升计算效率及搜索能力，为获取最优的多目标柔性车间的调度方案提供保证。最终应用实例仿真验证的方法评价算法的有效性与可行性,与初始调度方案中的最大完工时间、设备负载时间和能耗相比分别减少22.22%、2.79%和15.78%，延期时间减少了10 min。