统计模型在大坝安全监控中的研究及应用

黄红日，佟乃吉，王启龙

(辽宁省水利水电勘测设计研究院有限责任公司，沈阳 110006)

1 绪 论

在国民经济中大型建筑物的安全运行起着极为重要的作用，政府和地方部门对大型建筑物的安全监测部分十分重视。大型建筑物对能源的输入输出转化应用涉及到社会的各个领域，影响着区域经济，甚至于整个社会的经济发展。其中大坝的安全问题受到各级部门广泛关注。

如果我们可以依照以往的经验，通过建立相关准确的数学模型，以水位，温度等周围环境中主要影响大坝变形的因素作为自变量，大坝变形值作为因变量，预测大坝自然变形，发现异常变形后及时向相关部门反映情况，相关部门进行快速有效的排查，对病变部位原因进行分析，找到恰当的方式进行修改预防，就一定程度上减少了大坝失事比例。即便某大坝即将失事被判定无法挽回，那提前的发现和预警，采取恰当的措施，也会有效减少经济和财产的损失。

2 统计模型原理

统计模型是在具有较大的数据量的基础上，确定了影响因子的规律性后，以各个影响因子作为自变量，大坝变形值作为因变量，选取部分数据进行训练，初步进行模型确立，并通过验证比较，后期调试，确定变量与因变量之间关系的数学模型。分为多元线性回归模型和逐步回归统计模型2种[1]。文章采用多元线性回归模型进行研究。

3 多元线性回归模型原理

变形值往往是多种影响因素的综合反映，各个影响因子与主行为之间也不是明显的线性关系，因此在多元线性化回归模型中对这些因子做变量代换的处理[2]，具体过程如下：

首先多元线性回归方程数学模型为：

y+V=a0+a1x1+a2x2+a3x3+…akxk…+anxn

(1)

式中：{xn|n∈Z+}为温度水位等影响因子；{an|n∈R}为未知的待定系数，即各个影响因子的权重。但是往往在影响因子对变形量的研究中，并不是简单的线性关系，需要进行变量变换，例如在研究大坝顶部水平位移的研究中：

y=a0+a1H+a2H2+a3H3+a4T1+
a5T2+a6T3+a7Inθ

(2)

再通过平差计算中最通用方法最小二乘：

NA+W=0[1]

从而求出待定系数：

A= -N-1W

得到多元线性回归方程：

4 多元回归模型的应用分析

4.1 工程简介

实验中选取某大坝监测数据，此大坝枢纽工程正常蓄水位150.00m，此混凝土重力坝平面布置图见图1。

监测项目主要包括：倒垂线观测、引张线观测、视准线观测、静力水准测量，双金属标测量。主要测量水平位移与垂直位移。除此之外也对大坝外界环境资料进行观测。其中包括：坝区降水量、坝区上下游水位和坝区气温等。

4.2 比例系数求取

首先通过绘制水平位移与各个因子的散点图如图2～7所示。

根据散点图可以清晰的看到水平位移与各个因子的关系，可以看出大坝水平位移与水位因子的线性关系最强。

通过对训练数据的读取，即2014.7.17到2016.6.15实测数据中选取83组，利用最小二乘算出回归方程的比例系数见图8。

得到多元回归方程：y=33.2542+0.0220x1+0.0396x2-0.00077776x3-1.2022x4+0.9020x5-0.0253x6

4.3 拟合值求取

根据公式求取训练数据的拟合值，画出实测值与拟合值的比较曲线如图11，并列出实测值与拟合值对比表1。计算出模型中误差为0.96mm，模型效果良好。

续表1 实测值与拟合值对比表

续表1 实测值与拟合值对比表

4.4 多元回归方程检验

4.4.1 相关系数检验

求取该多元回归方程的相关系数如图12为0.9291，已知相关系数在0.8～1.0之间证明该方程回归效果较为良好。

4.4.2 F检验与P检验

本例F=79.8846>F0.05(6，76)=2.220(查表)，P=8.8396e-31<α=0.05多元回归方程线性关系显著性良好，计算结果如图13所示。

4.5 预报值解算与分析

经过检验可知多元回归方程良好，接着对2016.8.5到2017.8.25的40组实测数据水平位移进行预报并且与实测值比较，图14为实测值与预报值比较曲线，表2为实测值与预报值对比表。求出预报值中误差为1.59mm。

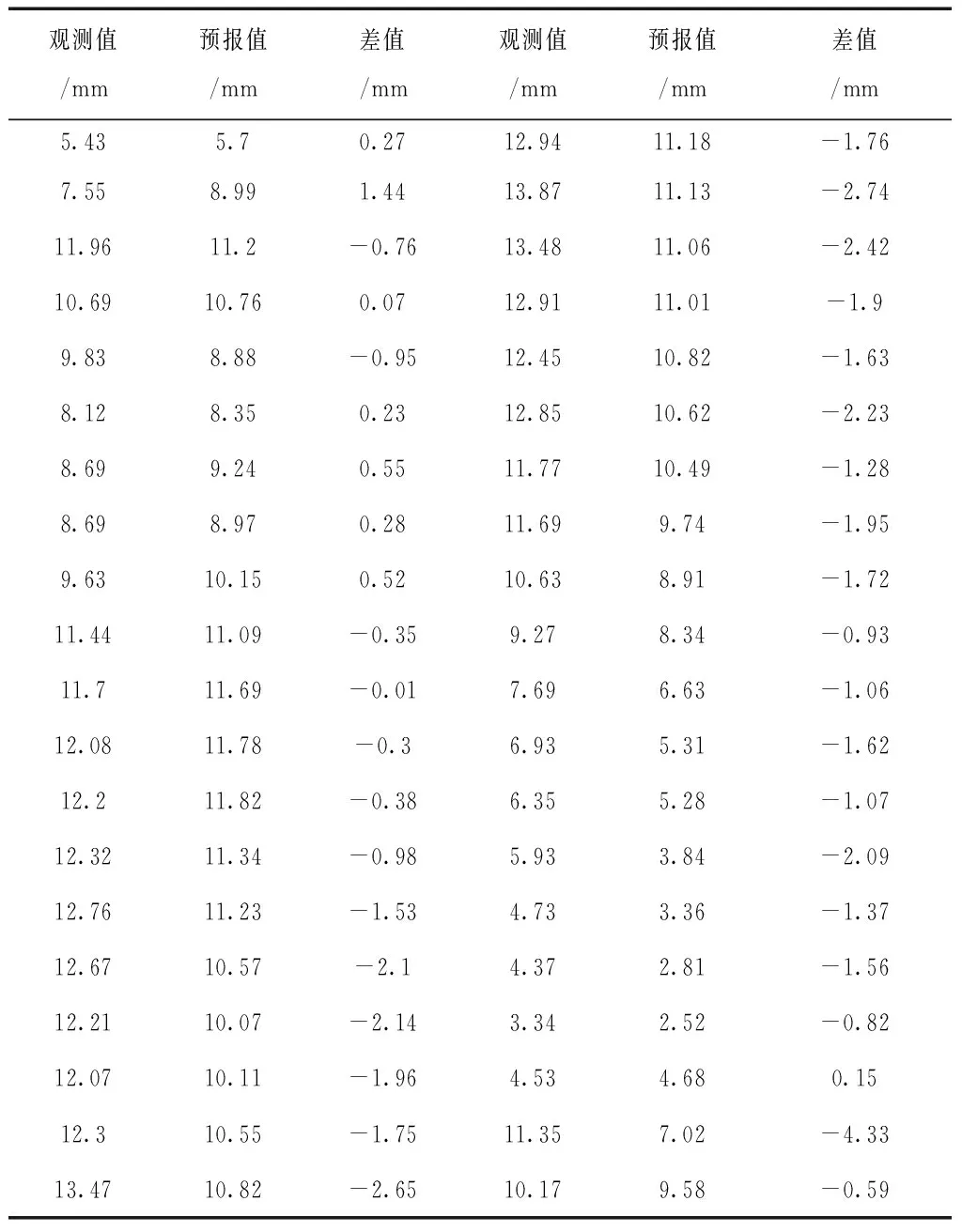
表2 实测值与预报值对比表

5 总 结

文章主要介绍了统计模型中的多元线性回归模型在大坝安全监测中的应用，通过经验分析确定影响大坝变形的影响因子，通过实验数据得到大坝位移量与影响因子之间的关系，最后将所得到的多元线性回归方程运用于检验数据，得到预测值，最后用所得预测值与实际值检验，判断所得多元线性回归方程的准确性。由最终结果得知本次针对此大坝建立的多元线性回归方程良好。

模型的不足之处：所需要的数据量大，造成数据冗余。模型的优点：数据量大所得的模型更有说服力。