分步式自适应学习参数辨识方法改进

高兴宇，付树兵，李 煜，陆佳琪

（桂林电子科技大学机电工程学院，广西 桂林 541004）

1 引言

六轴工业机器人因其通用性强、灵活性高、容错能力强、工作空间大等优势，在汽车、航空，军工以及电力等领域得到广泛使用。目前工业机器人普遍存在的问题是重复定位精度高，绝对定位精度低，限制了工业机器人在高端和高精密场合的推广和使用。

而提高机器人定位精度主要有两种方式：（一）提高机器人生产工艺、零件加工精度、整体装配精度。该方法对提高绝对定位精度作用不明显，同时成本骤增；（二）机器人精度标定，主要包含：运动学建模、误差测量、参数辨识、误差补偿。该方法可以显著提升机器人定位精度，是目前研究学者为提高机器人定位精度普遍使用的一种研究方法。其中，参数辨识是机器人精度标定的重点，由于冗余参数，部分相关参数的干扰，参数辨识精度低，误差补偿效果不理想。最终导致机器人绝对定位精度低的瓶颈一直没有得到很好的突破。

文献[1]以IRB120机器人为标定对象，利用奇异值分解与最小二乘法迭代法相结合的参数辨识方法，实现机器人的定位精度由标定前的0.5mm提高到标定后的0.3mm。文献[2]提出了一种基于几何约束的工业机器人运动学参数闭环标定法，长度偏差的标准差从标定前的2.2586mm减少到0.4998mm。文献[3]提出二级误差补偿，先后使用不同辨识方法对几何参数误差和非几何参数误差进行补偿，机器人的平均定位误差由4.1113mm 下降至1.0608mm。文献[4]研究直角坐标机器人的标定，机器人运动精度得到很大提升，但是不具有通用性。

目前大多数机器人误差补偿后末端定位最大误差仍停留在毫米级，为解决机器人辨识精度低，误差补偿效果差等问题，提出一种分步式自适应学习参数辨识方法，并用二分法区域搜索法改进算法，在X、Y、Z轴上，最大误差降低至0.1862mm。最终用MATLAB仿真验证，该算法辨识精度高，辨识结果稳定可靠，为机器人精度标定提供理论支撑。

2 运动学建模

目前的工业机器人主要采用D-H模型，当机器人相邻关节旋转轴线平行或者近乎平行时，存在奇异点，末端位置跳动较大。为解决以上问题并基于参数最少原则，采用D-H模型与MDH模型相结合，在关节旋转轴平行或者近乎平行时，引入绕Y轴的旋转参数β[5]，其余保留经典的D-H模型。

仍以viper650机器人为实验对象，坐标关系图，如图1所示。结构参数名义值，如表1所示。如未说明，MATLAB仿真各参数误差预设值，如表2所示。

图1 Viper650机器人坐标系关系图Fig.1 Viper650 Robot Coordinate System Diagram

表1 运动学参数名义值Tab.1 Nominal Value of Kinematic Parameters

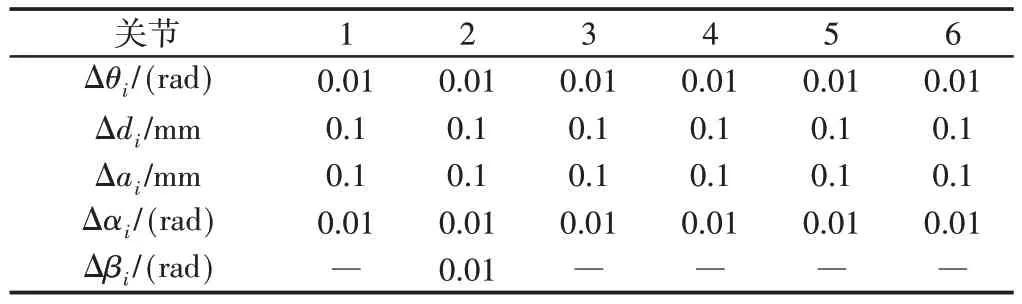
表2 运动学参数误差预设值Tab.2 Kinematic Parameter Error Preset

依据图1所示，相邻关节坐标系间的D-H变换矩阵为：

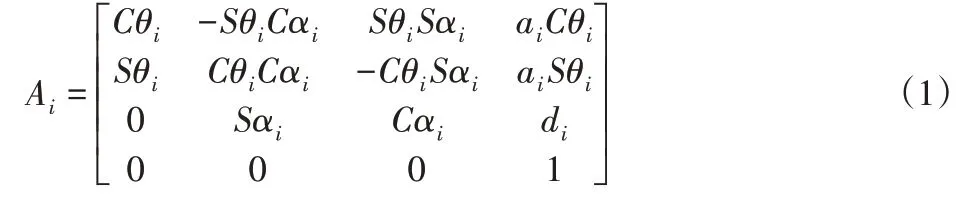
其中，2、3关节间的MDH变换矩阵为：

式中：C—cos；S—sin，i=1、3、4、5、6。最终机器人末端位姿矩阵：

式中：n(nx，ny，nz)、o(ox，oy，oz)、a(ax，ay，az)—机器人末端法兰相对于基坐标系的姿态向量；p(px，py，pz)—机器人末端执行器的位置向量。则末端位置误差：

式中：pr—实际位置；pn—名义位置［6］。

对末端位置进行微分处理，其误差模型如下［7］：

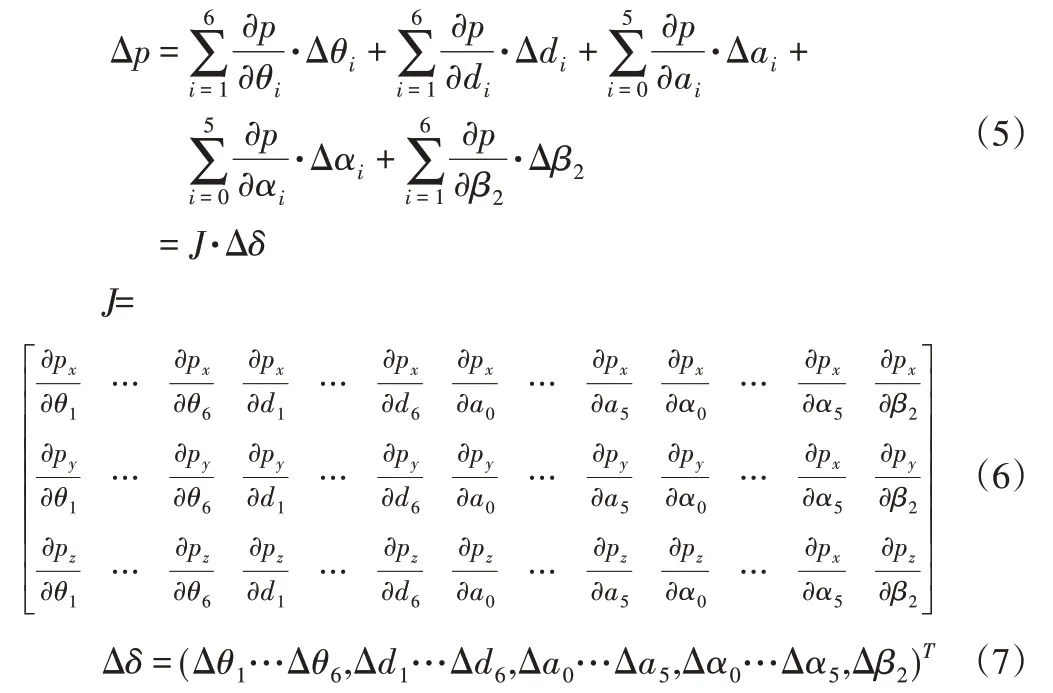
式中：J—（3×25）的机器人误差系数矩阵，又称雅克比矩阵；Δδ—（25×1）的几何误差参数矢量，以下参数辨识序列皆以此为准。整体需要辨识的参数为25 个，则要求测量点数N＞25/3。实际为了提高辨识精度，一般取N≥9构建超定方程组。当雅克比矩阵满足列满秩时，可直接进行参数辨识。

但在实际的机器人标定环节，由于机器人存在冗余参数，其秩rank(J)＜25，运算结果不唯一[8]。往往借助QR分解，对参数的冗余性进行分析，即：

式中：Q—N×N的正交矩阵；R—（25×25）的上三角矩阵，R矩阵对角线上的元素为J矩阵的列特征值。特征值为0的列代表不起作用参数所对应的参数列，特征值很小近乎为0的列代表相关参数列，不起作用参数以及部分相关参数属于冗余参数，在最小二乘算法中无法辨识。

QR分解特征值分布的整体和局部放大折线图，如图2、图3所示。传统最小二乘算法误差参数辨识结果，如图4所示。

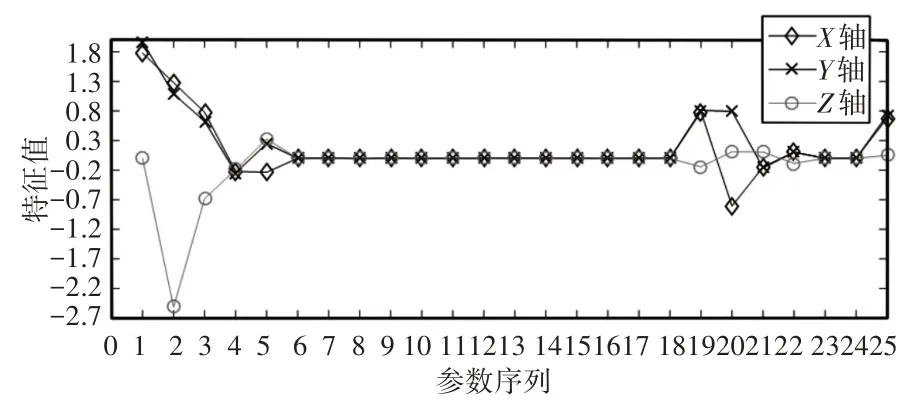
图2 QR分解特征值分布折线图（a）Fig.2 QR Decomposition Feature Value Distribution Line Chart（a）

图3 QR分解特征值分布折线图（b）Fig.3 QR Decomposition Feature Value Distribution Line Chart（b）

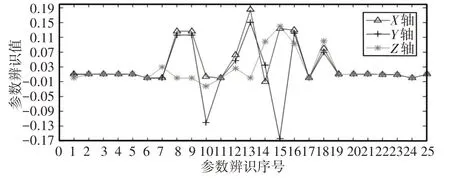
图4 最小二乘算法参数辨识折线图Fig.4 Least Squares Algorithm Parameter Identification Line Graph

根据图2～图4可以发现：

（1）杆长误差Δai和连杆偏移Δdi的特征值都基本趋向0，其辨识结果存在三种问题：

（a）辨识精度不高；

（b）X、Y、Z轴参数辨识结果不一致，波动性较大；

（c）部分相关参数无法辨识。

（2）Δθ6、Δα5、Δα6特征值为0，属于冗余参数；

（3）Δd5、Δa5特征值近乎为0，参数相关性较强，其对应的参数辨识结果几乎为零。

根据运动参数对末端位置精度影响特性[10]，Δθ6和Δα6的误差可以忽略，最终需要辨识的参数有23个。其中Δθi和Δαi的辨识采用传统的最小二乘法，基本满足辨识精度要求。

基于以上参数辨识问题，首次提出等步长区域搜索辨识Δdi和Δai，并最终采用二分法区域搜索完善辨识的精度和辨识结果的稳定性。

3 工业机器人误差模型参数辨识方法

根据研究，相同参数误差条件下，不同位姿对末端位置精度影响不同，理想的测量位姿对参数辨识起到事半功倍的效果。

因此在进行误差参数辨识之前，需要获取n组较为合适的位姿进行误差测量。并首次提出使用方差作为参数辨识稳定性指标。算法流程图，如图5、图6 所示。q11、q12、q13、q14、q15、q16代表Δdi i=1～6辨识结果。同理，p11、p12、p13、p14、p15、p16代表Δai i=1～6辨识结果。两者初始值为0。

图5 主流程图Fig.5 Main Flow Char

图6 二分法区域搜索流程图Fig.6 Dichotomous Region Search Flow Chart

在主流程图中，varmin首先预设值，当经过二分法区域搜索后，余下参数误差辨识完毕。然后根据当前整体辨识结果，对比参数误差补偿后方差是否变小。遍历n2组位姿数据，从中挑选参数误差辨识效果最好的一组位姿测量点。并输出误差补偿后最大定位偏差max、方差varmin、均值ave，以及参数辨识结果rtEr和测量位姿点关节角度信息th。

其中，th=[th1th2th3th4th5th6]T，代表从随机数中选取的40组较佳辨识位姿。在二分法区域搜索流程图中，lti，i=(1～12)代表二分法区域搜索初始值，llt为各参数停止区域搜索判断标准，var2为正向区域搜索补偿后定位偏差方差值，var3为负向区域搜索补偿后定位偏差方差值。通过对比补偿前后方差值是否改善，若正负搜索效果不佳，则当前误差参数步长二分化。其余参数辨识进行相同的搜索操作，直至各参数搜索步长都小于llt，则停止搜索，输出参数误差矩阵rtEr。

4 仿真分析

根据以上步骤选出测量位姿，并进行仿真实验。未标定前X、Y、Z轴误差分布，如图7所示。

图7 未标定前误差折线图Fig.7 Uncalibrated Front Error Line Chart

根据图7显示发现：

（1）当参数都存在微小误差时，对末端位置定位精度存在明显的误差积累效应；

（2）参数误差相同，测量点位姿不同，末端位置定位精度差异性较大，验证前者测量位姿选取的重要性；

（3）同一误差对X、Y、Z轴的定位精度存在差异性。

辨识误差补偿后在X、Y、Z轴上的误差折线图，如图8～图10所示。

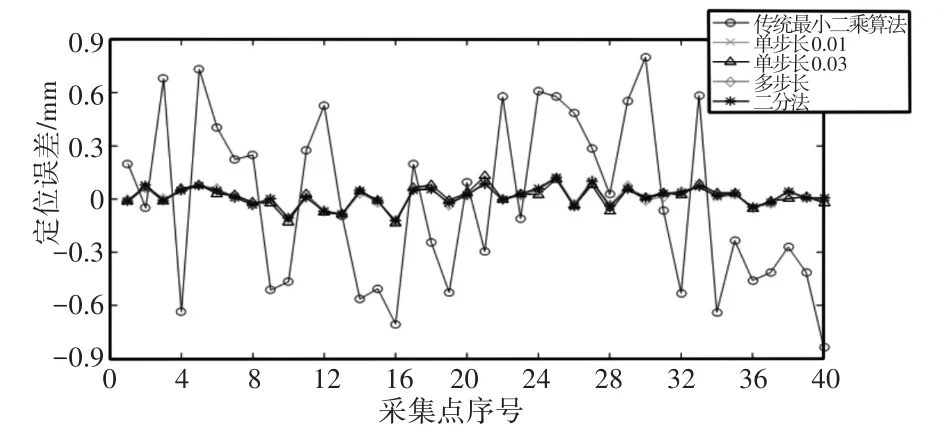
图8 X轴误差分布折线图（a）Fig.8 X-Axis Error Distribution Line Chart（a）

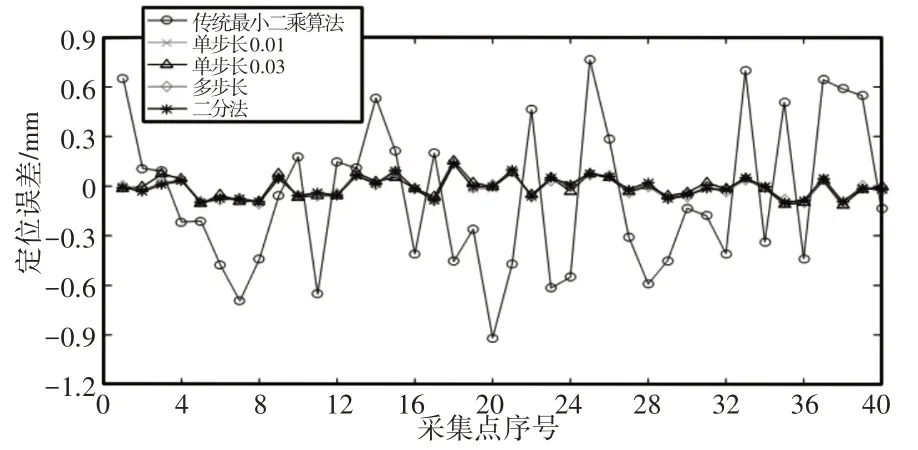
图9 Y轴误差分布折线图（a）Fig.9 Y-Axis Error Distribution Line Chart（a）

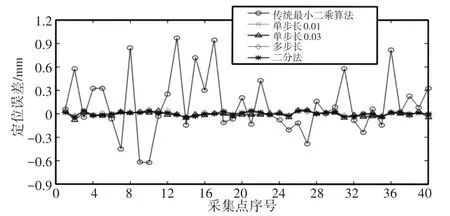
图10 Z轴误差分布折线图（a）Fig.10 Z-Axis Error Distribution Line Chart（a）

第一种辨识方法采用的是传统的最小二乘算法，不进行迭代处理。其余四种是自身提出的区域搜索方法，单步长0.01是搜索步长为0.01，单步长0.03是以0.03步长进行区域搜索。多步长是在单步长0.03的基础上，增加0.02和0.01步长搜索，增加部分只是放在单步长0.03的末尾，单次搜索，避免陷入局部最优，同时对参数辨识精度起到微调作用。

前面三种区域搜索都是采取等步长的搜索办法，辨识结果可能会陷入局部最优。最终提出二分法区域搜索，当初始值小于参数误差值时，搜索模式等同于等步长区域搜索。整个搜索过程是边搜索边补偿，所以搜索后期初始值大于参数误差值，进入二分法搜索模式。初始值大于或者小于参数误差值时，对参数辨识精度影响不大，但初始值不宜小于单步长的初始值，否者失去二分法意义。从图中可以发现，当参数误差较小时，区域搜索的辨识方法明显优于传统最小二乘算法，其误差补偿后曲线拟合度高，辨识精度高，结果差异性小。由前面的QR分解特征值分布图可以知道，转角Δθi和扭角Δαi辨识结果精度较高，杆长偏差Δai和连杆偏移Δdi特征值趋于0，参数相关性较强，辨识精度较低。

对杆长偏差Δai和连杆偏移Δdi重新设定预设值，如表3所示。其余参数误差保持不变。新误差预设值辨识补偿后，在X、Y、Z轴上的误差折线图，如图11～图13所示。

表3 杆长偏差和连杆偏移新预设值Tab.3 Rod Length Deviation and Link Offset New Preset

图11 X轴误差分布折线图（b）Fig.11 X-Axis Error Distribution Line Chart（b）

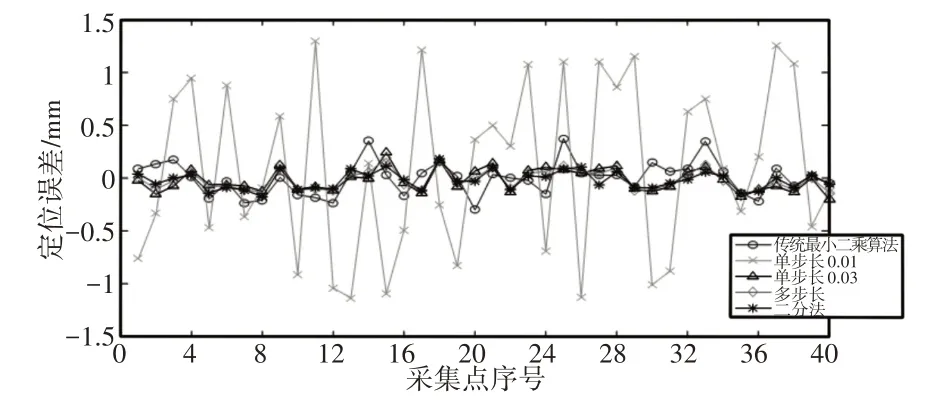
图12 Y轴误差分布折线图（b）Fig.12 Y-Axis Error Distribution Line Chart（b）

图13 Z轴误差分布折线图（b）Fig.13 Z-Axis Error Distribution Line Chart（b）

对比图8～图10，可得到：

（1）当参数误差值较大时，单步长0.01区域搜索陷入局部最优。证明：等步长区域搜索，步长不能设置过小；（2）当参数误差较大时，最小二乘算法辨识结果得到改善，参数相关性弱化；（3）多步长和单步长0.03的区域搜索补偿效果基本保持一致，但多步长补偿效果相对优越，说明微调有效；（4）二分法搜索补偿效果明显高于其他算法，特别在Z轴方向上的补偿。

最后进行算法稳定性仿真验证，参数误差的辨识精度低主要是由于杆长偏差Δai和连杆偏移Δdi的误差值辨识精度低或者陷入局部最优导致。所以对以上12个参数误差采用随机数分配，在（0，1）内产生30 组预设误差，每组参数辨识有40 个测量位姿点，整体实验基数较大，实验验证结果可靠。

以下的等步长区域搜索步长初始值都为0.03。30组预设误差补偿后最大定位误差分布折线图，如图14所示。30组预设误差补偿后均值误差分布折线图，如图15所示。30组预设误差补偿后定位误差方差分布折线图，如图16所示。

图14 预设误差补偿后最大定位误差Fig.14 Maximum Positioning Error After Preset Error Compensation

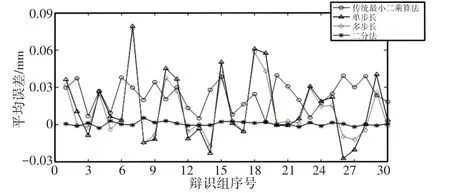
图15 预设误差补偿后均值误差Fig.15 Mean Error After Preset Error Compensation

图16 预设误差补偿后方差Fig.16 Variance After Preset Error Compensation

通过图14～图16，可以知道：

（1）二分法辨识精度最高，参数误差补偿后，最大定位误差在0.2mm以内；（2）二分法辨识精度最高，参数误差补偿后，定位误差均值趋于0；（3）二分法辨识精度稳定，参数误差补偿后，定位误差方差稳定趋于0。

不同算法补偿后，最大定位误差对比情况，如表4所示。

表4 最大误差对照表Tab.4 Maximum Error Comparison Table

由表4可以知道，二分法区域搜索相对传统最小二乘算法、单步长区域搜索法、多步长区域搜索法最大定位误差分别下降了81.37%、70.73%、67.21%。最终验证了二分法区域搜索误差参数辨识的高精度、高可靠性。

5 结语

针对工业机器人标定环节参数辨识精度低，参数误差补偿不理想等问题，提出一种分步式自适应学习参数辨识方法。并对该算法进行改进，采用二分法区域搜索辨识参数误差Δdi、Δai，i=(1～6)。算法改进后，克服了等步长区域搜索陷入局部最优问题，同时参数误差辨识精度更高。参数误差补偿后，末端定位在X、Y、Z轴上的最大偏差降低至0.2mm 以内，说明该辨识算法有效。并在测量位姿选定后，参数误差Δdi、Δai，i=(1～6）在［0，1］内随机产生30 组预设误差。通过二分法区域搜索辨识参数误差，误差补偿后末端定位最大偏差仍保持在0.2mm以内，说明该算法稳定可靠。