燃料电池汽车双层模糊控制能量管理策略
于瀛霄,孙 闫,夏长高,韩江义,史金钟,高海宇
(1.江苏大学 汽车与交通工程学院, 江苏 镇江 212013;2.拖拉机动力系统国家重点实验室, 河南 洛阳 471039; 3.德燃动力科技有限公司, 浙江 嘉兴 314000)
0 引言
能源危机与全球气候问题是限制内燃机汽车发展的重要因素[1]。随着氢能技术的愈发成熟,质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)逐渐应用于新能源汽车[2]。PEMFC有着高能量密度、高转换效率等优势,但其本身结构及材料的理化性质等因素导致了PEMFC的动态特性较差,输出特性偏软,不能适用于频繁的变载工况[3],同时燃料电池只能将化学能转换为电能,能量转换的单向性导致其无法回收制动能量。因此,燃料电池电动汽车(fuel cell electric vehicle,FCEV)通常都配备了动力电池或者超级电容,一方面,可以通过电池或者超级电容回收制动能量。另一方面,在负载需求较大时,由电池或超级电容提供大功率,从而达到给燃料电池输出功率“削峰填谷”的作用。采用燃料电池+电池或者燃料电池+超级电容的车辆可以提升续航能力,也能够使车辆适应更加复杂的行驶工况,同时还可以有效提升燃料电池的使用寿命。
多电源的能量管理策略(energy management strategy,EMS)是影响整车动力性、经济性以及耐久性的重要因素[4]。车辆在实际行驶过程中,工况处于实时变化的状态,对于复杂多变的被控对象,传统的控制方法往往效果不佳。模糊控制能够将系统精确量模糊化,利用专家经验进行非线性控制[5]。这种方法不需要量化的参考变量,具有控制逻辑简单,易于实现等优势[6]。在FCEV中,模糊控制需要结合不同的需求以及部件状态,实时更新燃料电池输出功率。Che等[7]提出了基于自适应方法的模糊控制策略,用于控制燃料电池与电池之间的功率流,使SOC保持在良好范围内。Saib等[8]将需求功率、需求功率误差以及电池SOC作为模糊控制器输入参数,控制燃料电池输出功率,提升了FC的动态响应。Gao等[9]为了解决燃料电池系统响应慢等缺点,利用模糊控制器优化了系统功率分配,并通过实验验证了方法的有效性。因此,模糊控制在燃料电池输出功率控制方面具有较好的适用性。
在FCEV的实际行驶过程中,复杂的运行工况对燃料电池的使用寿命有着重要的影响[10]。研究表明,变载、启停、空载、大功率输出工况会加速燃料电池性能衰退。Song等[11]构建了燃料电池耐久模型,考虑了燃料电池性能衰退成本及能耗成本,利用庞德里亚金极小值原理优化了车辆能耗。降低了系统总运行成本。Zhang等[12]为了降低燃料电池变载对使用寿命的影响,在系统中配置了3个子燃料电池作为燃料电池系统。各个子燃料电池分别工作在固定工况,通过协调不同燃料电池之间的启停控制来实现输出功率的分级控制。Wu等[13]提出了一种鲁棒在线EMS来处理不确定的行驶周期,引入一个惩罚系数修正燃料电池输出功率,降低了燃料电池的输出功率的变化。因此,在制定模糊控制策略时,不仅要考虑整车经济性,更要考虑燃料电池寿命的保护。
传统模糊控制主要解决多电源能量分配问题,同时以减少运行成本、提升部件使用寿命或降低能源消耗为目标对模糊控制的隶属度函数分布进行优化,但是很少有学者考虑燃料电池实际的输出特性。当负载需求快速上升时,传统模糊控制会控制燃料电池目标输出电流跟随负载快速上升,而燃料电池在实际使用过程中内部化学反应需要一定时间,且由于空压机叶片具有惯性导致压缩空气无法立刻满足化学反应所需的流量,所以现阶段燃料电池的动态输出特性往往较差,无法适应车辆频繁变化的负载特性需求,而传统的模糊控制策略只能通过复杂的规则设定、减小燃料电池的目标输出电流范围,或者将负载高频变化的部分由电池来承担,以此来约束燃料电池电流的变化率,但该方法难以适应不同的道路工况,且规则制定更加复杂,整车经济性也往往较差。
本文主要基于上述问题提出了一种双层模糊控制策略,第一层模糊控制解决了多电源能量实时分配问题,第二层模糊控制限制了燃料电池电流的变化速率。另外,构造了兼顾能耗及部件耐久损耗的运行成本函数,利用人工蜂群优化算法,从全局优化的角度训练出了最佳的模糊控制隶属度函数组合以及模糊规则权重。该方法既解决了双电源能量分配的问题,并保证了燃料电池的实际动态输出特性在合理范围之内,又有效降低了整车运行成本,提升了部件使用寿命。
1 动力系统结构及模型
1.1 动力系统结构
本文动力系统及车辆模型是基于Zotye®X5紧凑型SUV建立的,并在现有平台上改进动力系统。其结构如图1所示。
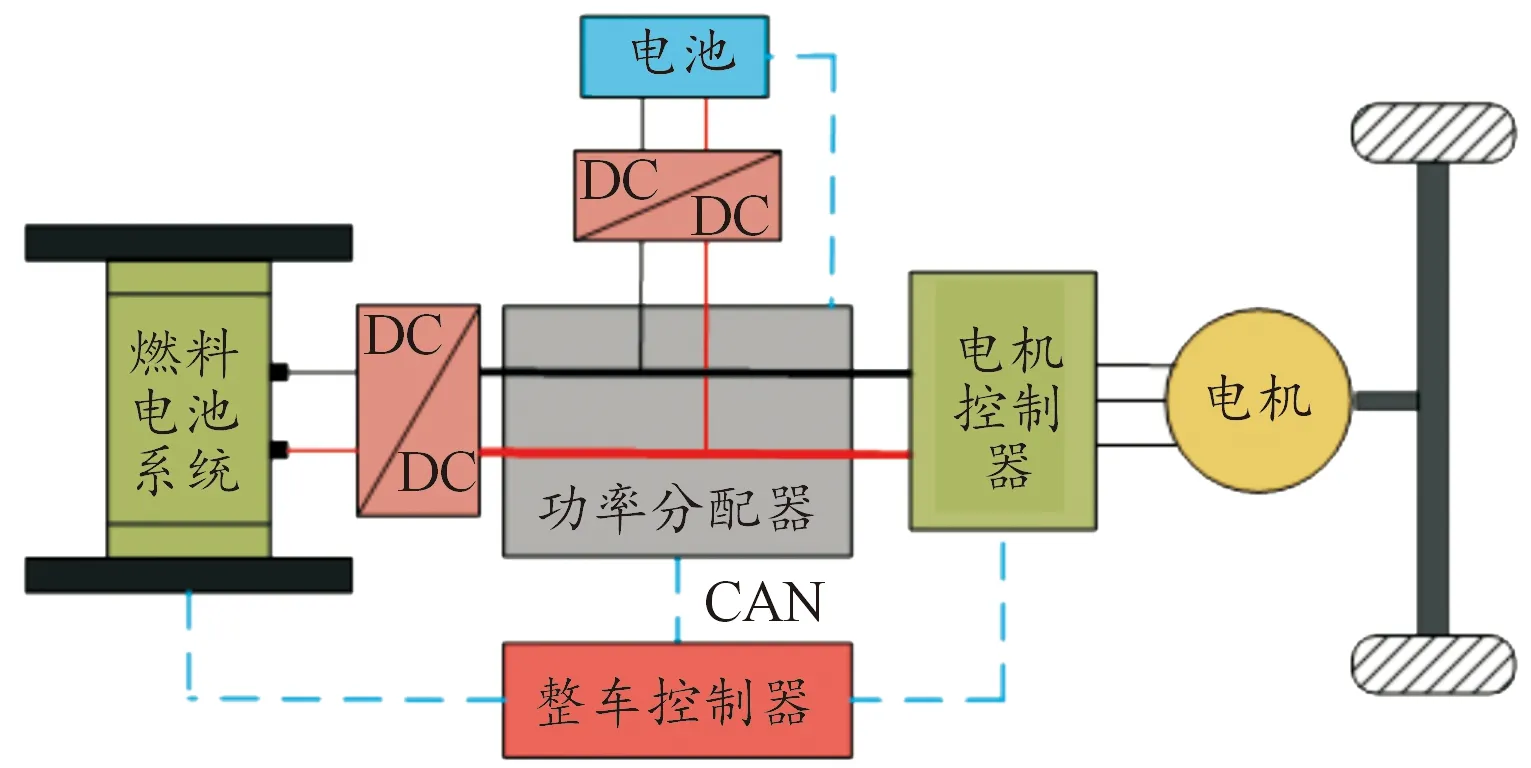
图1 动力系统结构示意图
整车动力系统主要包括燃料电池系统、电池、单向DC/DC变换器、双向DC/DC变换器、功率分配器、整车控制器、电机控制器、电机等。车辆在行驶过程中,整车控制器接收驾驶员功率需求信号,并计算出扭矩命信号发送给电机控制器,电机控制器根据扭矩命令信号计算出电流需求,功率分配器接收电机控制器计算出的电流需求信号,并按既定策略将其分配给动力电池与燃料电池。车辆与动力系统及部分零部件参数见表1。

表1 车辆与动力系统及部分零部件参数
1.2 纵向动力学模型
根据车辆纵向动力学方程计算车辆受到的总阻力,如下[14]:
(1)
式中:Ft为牵引阻力,Cr为滚动阻力系数,θ为坡度,Cd为空气阻力系数,A为迎风面积,δm为旋转质量系数,ρ为空气密度,V为车辆速度,a为车辆加速度。
车辆根据当前车速V和牵引力Ft获得需求功率Preq,如式(2)所示:
Preq=Ft·V
(2)
1.3 燃料电池系统模型
燃料电池的工作效率与当前系统的氢气消耗率有关,而氢气消耗率与系统输出电流成非线性比例关系。燃料电池系统氢气消耗、输出电流以及工作效率之间的关系如下:
Ifc=Icell·N
(3)
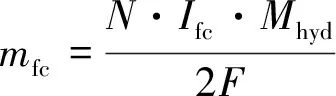
(4)
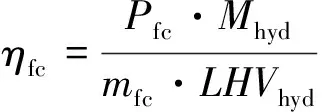
(5)
式中:Icell为电堆单体电流,N为电堆单体个数,mfc为系统瞬时氢气消耗速率,Ifc为燃料电池系统输出电流,Mhyd为氢气摩尔质量,F为法拉第常数,LHVhyd表示氢气低热值。
本文在实验室环境中,搭建了燃料电池系统测试台架(图2),用以测试系统特性曲线。主要部件包括电堆、氢气循环泵、燃料电池控制器、空压机、冷却系统、模拟负载。

图2 燃料电池系统测试台架
在诸多影响耐久性的因素中,变载占据主导地位。燃料电池变载能力受到空压机功率限制。本文所用的燃料电池系统实际变载能力通过台架试验测得,为5 A/s。本文通过台架试验得出了燃料电池V-A特性、氢气消耗以及效率曲线,见图3。
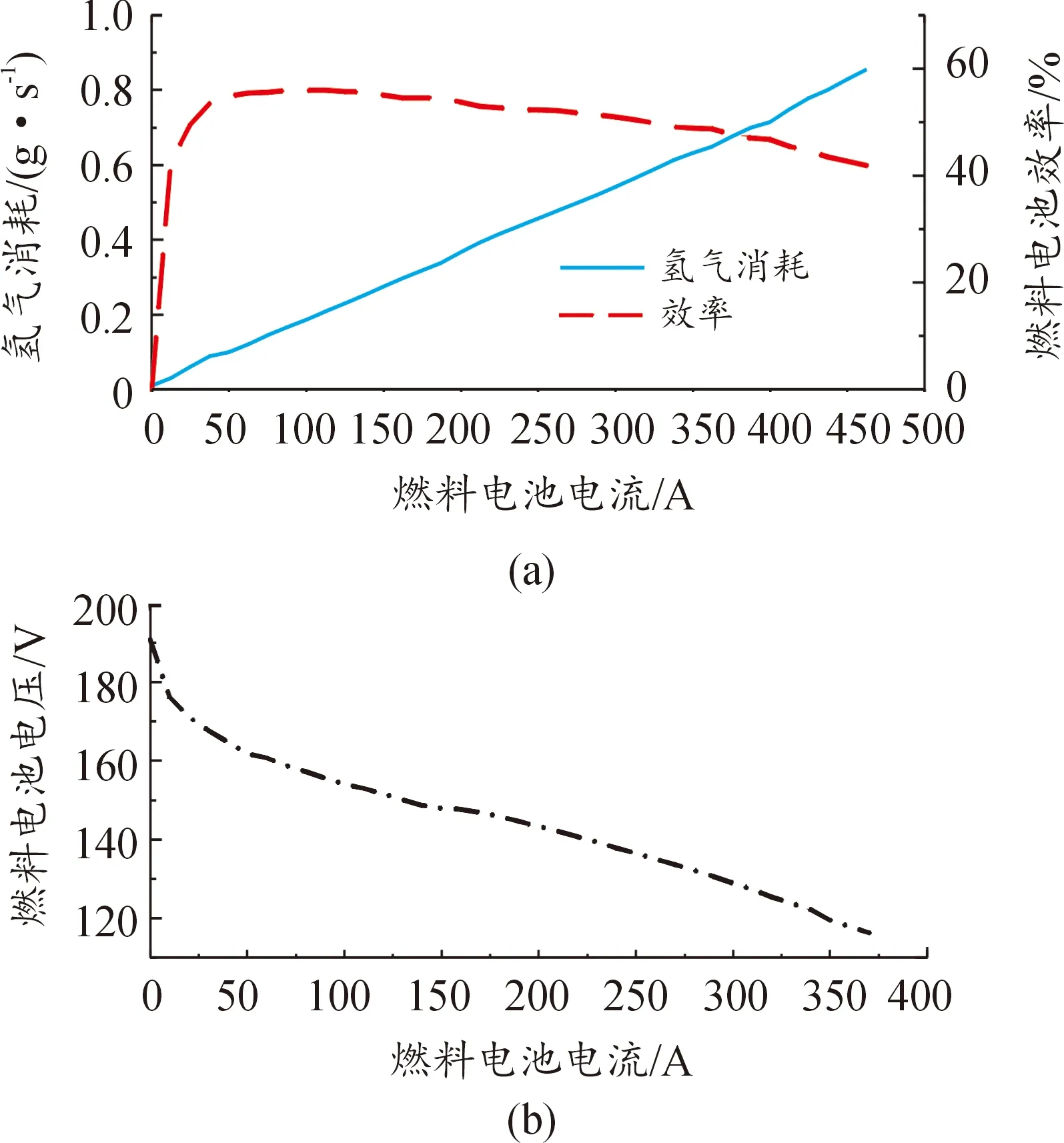
图3 燃料电池V-A特性、氢气消耗以及效率曲线
燃料电池运行过程中影响其耐久性的不利工况主要包括变载、启停、怠速以及过载等。建立燃料电池耐久损耗模型如下[15]:
Dfc=dchange+don-off+didling+dhigh
(6)
式中:Dfc为燃料电池总性能衰退百分比,dchange、don-off、idling、dhigh为由变载、启停、怠速、过载导致的燃料电池性能衰退百分比。
1.4 电池模型
电池采用等效内阻模型。电池功率、输出电流、内阻和SOC之间的关系如下[16]:
(7)
(8)
式中:Pbat为电池输出功率,Vocv为开路电压,Ibat为输出电流,Rbat为电池内阻,ηbat为库伦效率,Cbat为电池容量。
1.5 电机模型
在车辆运行过程中,电机根据VCU发送的扭矩命令和当前电机转速计算电机电流需求。燃料电池和电池的功率分配问题就转换为电流分配问题[17]。建立的电机模型如下[18]:
Pmot=ηmot·Pelc
(9)
(10)
式中:Pelc为电池和燃料电池提供的电功率,Pmot为电机输出的机械功率,ηmot为电机转换效率,Ireq为需求电流,Plost为电机损失功率,Vmot为电机电压。
2 能量管理策略
2.1 模糊控制策略
对于一些复杂被控对象,系统中某些控制变量往往不容易量化,运用常规的控制方法不易对其进行精准控制。首先构建了顶层控制逻辑,通过有限状态机划分整车运行状态,如制动能量回收、停车、电池单独供电、协同供电,并定义了各个状态的准入准出条件,其顶层控制逻辑如图4所示。图4中,SOCswitch、SOClow分别表示燃料电池开启时的电池SOC值以及电池SOC下限,SOCint表示电池初始SOC值;Ifc表示燃料电池输出电流,其大小由下文2.2节双层模糊控制决定;Ibat表示电池输出电流;H2表示系统氢气实时消耗量;H2con表示系统氢气总储量。
在顶层控制逻辑中,SOCint为90%,SOCswitch为40%,SOClow为10%。开始时,电池SOC较高,车辆以纯电动模式运行,此时电池单独满足驱动电机电流需求;当SOC降低至40%时,开启燃料电池并以Ifc进行输出;如果需求电流Ireq>Ifc,燃料电池和动力电池共同为车辆提供动力,如果Ireq≤Ifc,燃料电池单独驱动电机并且多余的电流(Ifc-Ireq)给电池充电。最后当SOC升高至40%时,关闭燃料电池,车辆回到纯电动模式。如此循环持续至氢气消耗完毕,最后进入纯电动模式直至SOC降低至10%。

图4 顶层控制结构示意图
2.2 双层模糊控制
为了实现变载限制以及变载大小控制,提出一种双层模糊控制方法,如图5所示。
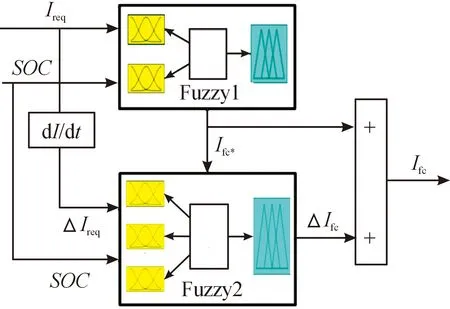
图5 双层模糊控制结构示意图
第一层模糊控制以需求电流Ireq和电池SOC为输入,输出为燃料电池电流Ifc*,并约束Ifc*在其高效区内。第二层模糊控制的输入为一级模糊输出Ifc*、电池实时SOC以及需求电流变化ΔIreq,输出为燃料电池输出电流变化速率ΔIfc,并约束ΔIfc在5 A/s以内,即ΔIfc≤5 A/s。
如前文所述,传统一层的模糊控制虽然对燃料电池输出电流进行了合理控制,但未考虑燃料电池变载能力限制。在顶层控制策略中,当SOCswitch较小(≤40%),在完整的续驶里程循环中燃料电池发生启停的次数非常少。根据式(7),由启停和怠速带来的耐久损耗可以忽略。另外,由于第一层模糊限制Ifc在高效率区,此时电流相对较小,由过载导致的耐久损耗也可以忽略。因此,变载是策略需要重点考虑的因素。
当检测到第一层模糊控制(Fuzzy1)输出的Ifc变化率dIfc>5时,第一层模糊输出为Ifc*,第二层模糊不生效且ΔIfc=5,燃料电池最终输出电流为Ifc=Ifc*+5。当检测到dIfc≤5时,第二层模糊控制器生效,根据第二层模糊控制的输入实时控制ΔIfc的大小,此时Ifc=Ifc*+ΔIfc。
这样,燃料电池实际输出电流变化速率能够被限制在要求的范围之内,同时其输出功率大小也能被约束在高效区内。
2.3 人工蜂群算法优化过程
双层模糊控制解决了需求电流分配的问题,同时也约束了燃料电池电流的变化范围。然而,模糊规则及权重系数的设置均基于个人经验,规则的制定具有很强的主观性,控制效果也非最优。本文综合考虑能量消耗与燃料电池耐久损耗构造了综合能耗评价函数,如式(11):
Qcon=conhyd·Chyd/mile+Qbat·Cbat/mile+
Dfc·Cfc·Pfcmax/(mile·20)
(11)
式中:Qcon为评价指标,代表了单位里程的运行成本,conhyd为总氢气消耗,Qbat为电池容量,Pfcmax为燃料电池最大功率,mile为续驶里程,20%为本文允许的燃料电池最大衰退百分比,当燃料电池性能衰退大于20%时,燃料电池将无法继续使用。Chyd、Cbat、Cfc分别为氢气价格、市电价格、每千瓦燃料电池系统价格。
本文以式(11)作为全局优化函数,并通过人工蜂群算法(artificial bee colony algorithm,ABC)进行迭代寻优,优化对象为双层模糊控制的隶属度函数及权重系数。优化过程如下:将各个隶属度函数端点以及顶点依次作为ABC算法的向量,令其为(X1,X2,X3…)。同样地,各个模糊规则的权重也作为算法的向量。图6(a)展示了ABC优化隶属度函数设置方法。图6(b)为ABC寻优过程。通过商业软件Amesim计算一次补充能源车辆需时里程,并结合氢气消耗、燃料电池性能衰退量及电池电能消耗在Simulink中计算出单位里程运行成本,最后通过Matlab.m脚本文件不断更新ABC雇佣蜂和引领蜂的数量及位置,直到寻找到最小运行成本。此时,对应的隶属度函数分布以及模糊规则权重即为最终优化结果。通过离线优化的方式使隶属度函数及权重因子不再依赖人工制定,结果更具客观性。
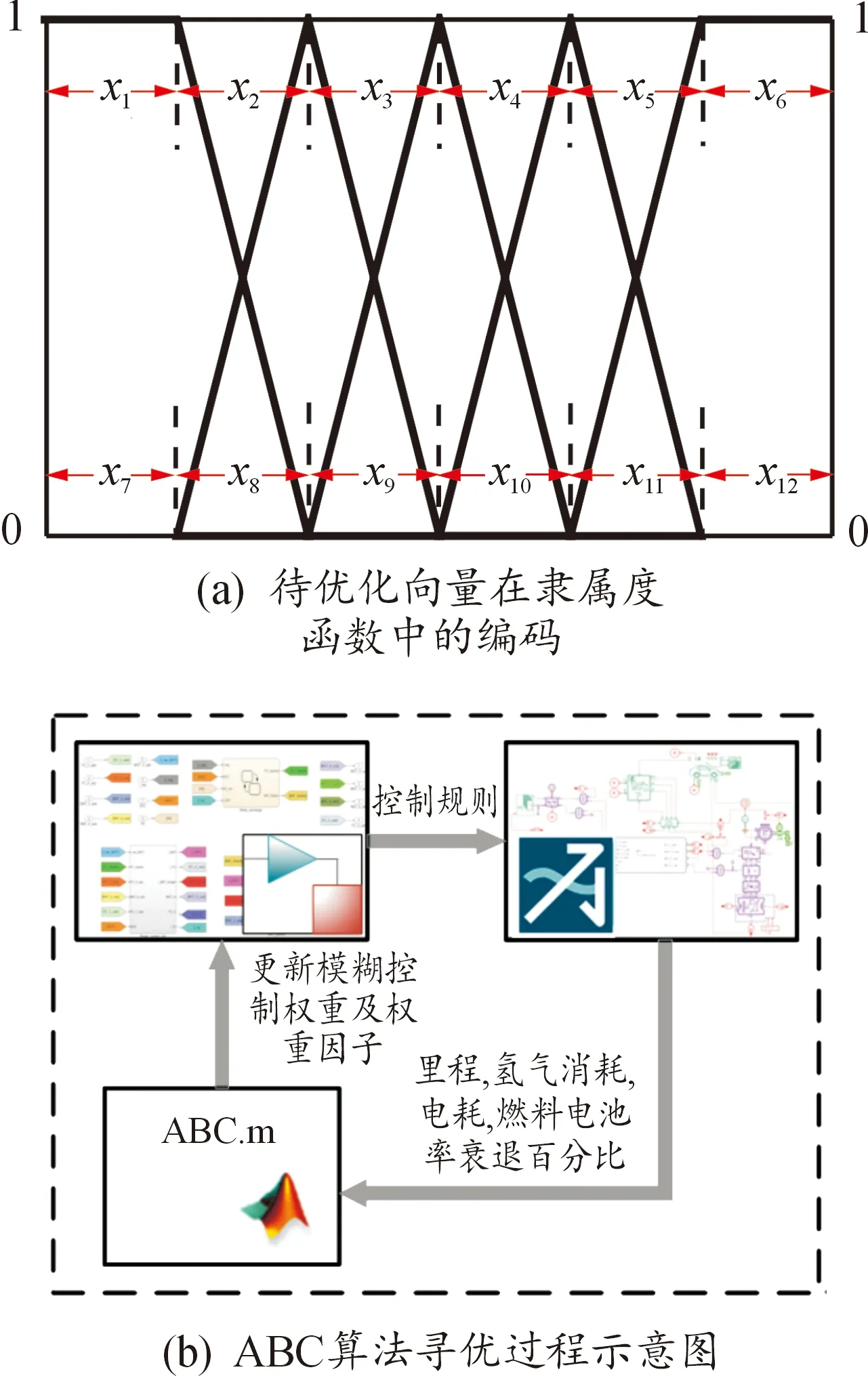
图6 ABC算法优化原理
3 结果与讨论
通过ABC算法迭代寻优的方式,找到最优的隶属度函数分布以及模糊规则权重组合,使成本函数最低。经过1 000次迭代计算后,Fuzzy1的隶属度函数分布以及权重因子如图7—8所示。Fuzzy2优化的方式和Fuzzy1相同。

图7 ABC算法优化前后的隶属度函数
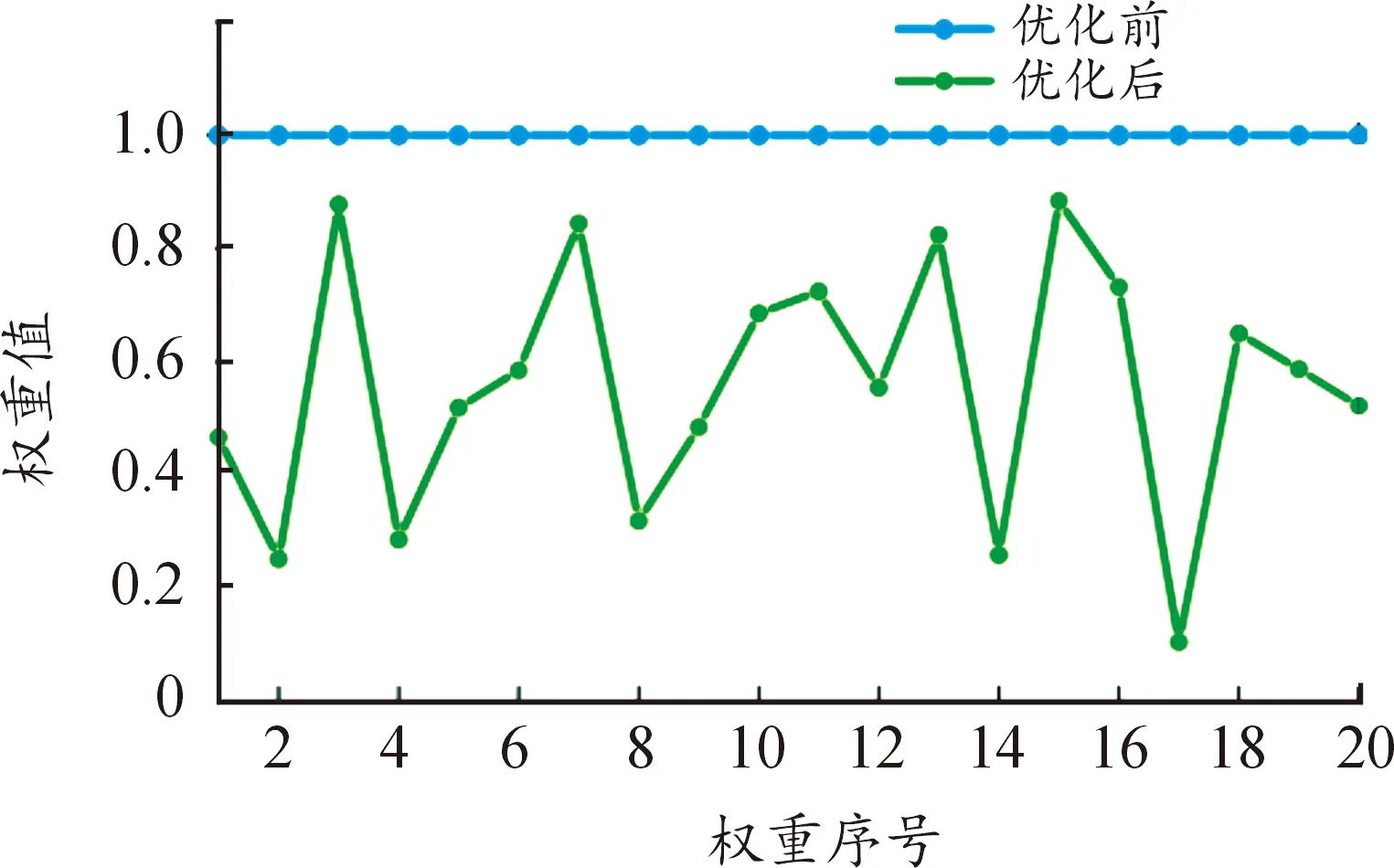
图8 ABC算法优化前后的权重因子
为了验证策略的可行性与优越性,本文选择典型工况WLTP和UDDS进行仿真与优化,这2个工况都拥有较为频繁的速度变化。图9展示了在2种工况下的部分需求电流、电池SOC以及电池电流仿真结果。需要注意的是,在实际仿真中软件需求电流为正或零表示车辆处于制动和滑行状态,反之车辆处于驱动状态。电池电流为正表示充电,反之为放电。根据图9可知,当电池SOC较低且车辆在制动或滑行状态下,燃料电池保持开启为锂电池充电,使其SOC快速回升。但由于顶层控制逻辑及双层模糊协同控制策略,当电池SOC将要到达40%,燃料电池即将关闭时,通过控制减小燃料电池输出电流,并增大电池输出电流而使其SOC处于接近但小于40%的状态,此时燃料电池不会因为到达40%而关闭,燃料电池启停次数可以有效降低,且电池SOC波动不会太大并趋于稳定,该现象可由图中SOC变化曲线看出。

图9 不同工况下的部分需求电流、电池SOC、电池电流曲线
图10展示了在2种工况下的燃料电池电流及变化率仿真结果。图10 (Ⅰ) 表示经过双层模糊控制后的燃料电池输出电流变化率ΔIfc的变化趋势。由图可以看出,燃料电池电流变化率可以被约束在5 A/s的范围内。图10(a) (Ⅱ)及图10(b) (Ⅱ)为经过人工蜂群算法优化前后的燃料电池实际输出电流。可以看出,当ΔIfc较大时,第二层模糊控制开始起作用,限制了燃料电池输出电流的变化速率。尤其是在负载增大时,燃料电池输出电流并没有跟随负载快速增大,而是被限制在5 A以内,并由电池承担了负载增大的部分。在满足变载要求的前提下,降低了燃料电池系统电流变化速率,这对提升燃料电池耐久性是有利的。
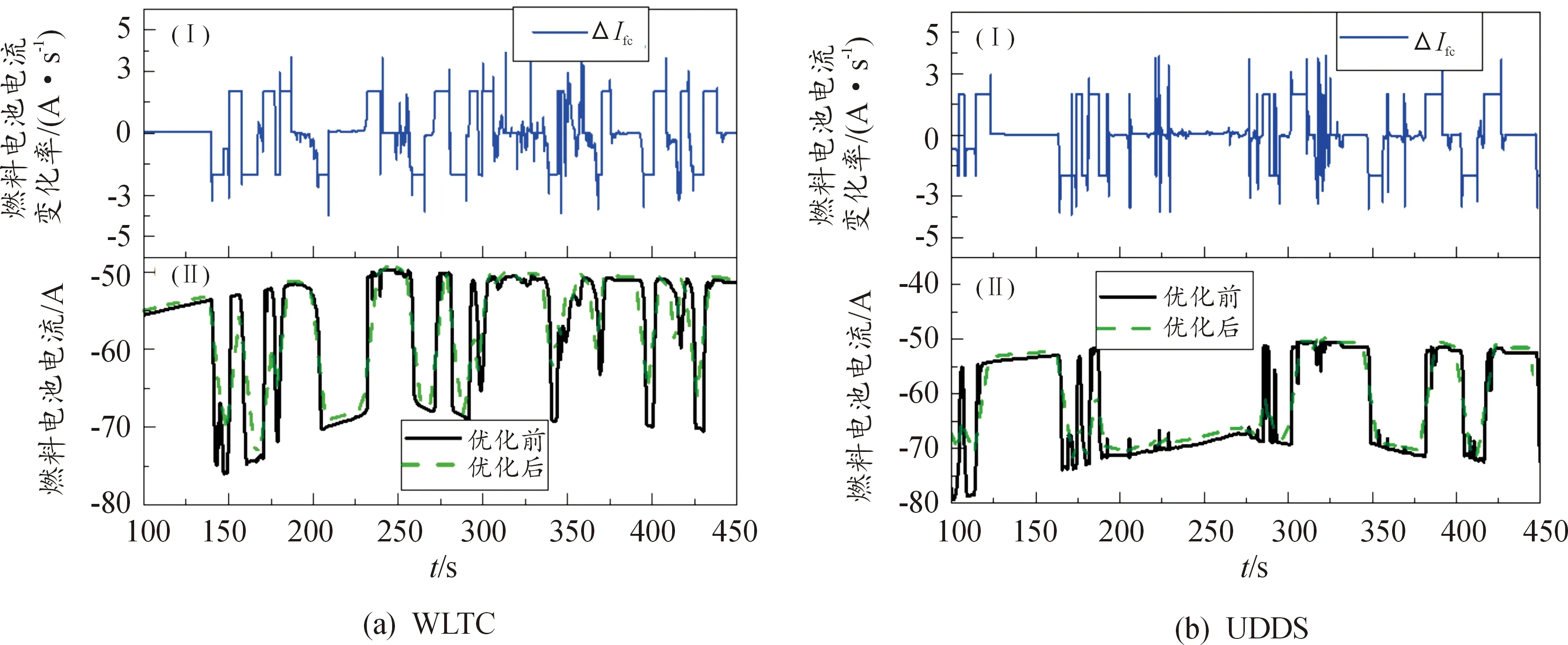
图10 不同工况下燃料电池电流及变化率曲线
进一步的仿真中,WLTC工况下,优化前后的续驶里程分别为238.12、264.79 km。UDDS工况下,优化前后的续驶里程分别为287.72、313.08 km。可以看出,双层模糊控制在优化燃料电池变载速率的同时,提升了整车经济性。这也间接说明,基于成本函数优化的模糊控制是优于基于人工经验的模糊控制的。
4 结论
本文提出了一种双层模糊控制方法,降低了燃料电池变载速率,提升了燃料电池系统耐久性。通过ABC优化算法,寻优最佳隶属度函数分布以及模糊规则权重组合,降低了总运行成本。首先通过台架试验的方式获取了燃料电池输出特性及实际变载能力,搭建了燃料电池耐久模型。其次提出了双层模糊控制策略,第一层模糊控制将电池SOC与需求电流作为模糊控制的输入,动态调整燃料电池输出电流并将其限制在系统高效率区内,第二层模糊控制将燃料电池变载速率控制在变载能力以内,同时降低燃料电池的耐久损耗。最后通过ABC算法优化双层模糊控制的隶属度函数及权重系数。本文采用理论建模与仿真计算相结合的方式验证了上述策略的可行性。仿真结果表明:所提出的双层模糊控制策略能够在保证经济性的前提下限制燃料电池的变载速率,降低耐久损耗,在WLTC与UDDS典型工况下,能够优化续驶里程,优化比例分别为11.2%、8.79%。

