基于GPU的雷达成像加权相位自聚焦技术
张晓洋 张开生 张 军
(西安电子工程研究所 西安 710100)
0 引言
近年来,伴随着图形处理器(Graphic Processing Unit, GPU)的快速发展,GPU已经成为具备强大并行化能力的多核处理器。传统雷达信号实时处理架构主要通过FPGA(Field-Programmable Gate Array)与DSP (Digital Signal Processing)来实现,而单片DSP的算力已无法满足实时雷达成像算法的性能需求。因此在实际应用中多需要通过多片DSP联合对数据进行处理。该做法往往无法适应机载雷达等对功耗、尺寸有高限制的应用场景。而利用GPU对雷达成像信号处理进行软件化实现,不仅能够提升信号处理速度,同时软件化信号处理也将便于系统开发与维护。NVIDIA于2006年推出的基于GPU的通用并行计算架构(Compute Unified Device Architecture,CUDA)为开发人员对GPU硬件的使用提供了便利。
目前,研究人员对雷达成像算法的GPU 并行优化开展了大量研究。文献[2]在Arm Mali-T860 GPU平台上对雷达成像算法中的多视处理、旋转放缩和图像量化算法进行了并行优化设计。文献[3]对常用机载频域成像进行了并行化分析与实现。文献[4]对基于CS(Chirp scaling)原理的两步去斜成像算法进行了嵌入式GPU实现的研究。对于雷达成像过程中因平台运动误差所造成的雷达成像散焦情况,在利用惯导数据进行粗补偿的同时,通常采用基于回波信号的自聚焦算法实现精补偿。该算法中大量快速傅里叶变换、转置、向量点乘等运算均适合利用GPU的多核结构来实现高性能并行处理。文献[5]对基于Tesla C2050显卡平台的传统相位自聚焦算法进行了并行化分析与实现,文献[8]所提加权极大似然PGA(Weighted Maximum Likelihood PGA,WML-PGA)算法能够相比于文献[5]所用传统PGA算法提升了相位梯度估计的精度,同时Tesla C2050显卡对于机载平台的使用尺寸、功耗均不能满足要求,故本文提出基于嵌入式GPU平台Tx2对加权PGA算法进行了并行化分析与实现,并通过实验对本文所提技术的性能同TMS320C6678平台进行了对比实验。
1 加权相位梯度自聚焦PGA原理
相位梯度自聚焦是应用广泛的一种相位补偿方法,该算法利用图像的自聚焦性,不依赖于模型。假设同一距离单元内的相位误差是不随时间变化的,通过估计不同距离单元的相位误差梯度估计相位误差,同时利用同一距离单元内的相干积累减少噪声对相位误差梯度估计的影响。该算法基于图像中某些特定点的散焦状况进行自聚焦处理的,从而使整个图像因相位误差造成的散焦情况得到改善。而WML-PGA在此基础上通过对不同距离单元的平坦度进行加权计算,提升相干积累时平坦度高的距离向影响力,从而提升相位误差估计精度与收敛速度,该算法具体实现步骤如下所述。
1.1 方位去斜
雷达成像算法中可以证明方位向信号的频率随着时间呈现线性变化,其中方位向信号斜率、二次相位分别为

(1)

(2)
在相位梯度估计之前对信号进行方位去斜,用来去除信号的二次调频分量。
1.2 样本选择
为了便于工程实现,PGA算法将整个方位向滑动分为个长度的子孔径波束,其中各个子孔径之间滑动重叠2的位置,这样的做法可以避免相位误差估计时各子孔径所估计的相位之间出现跳变所导致的成像算法在方位脉压时的性能恶化。同时为了提升相位梯度估计时的信杂比,在选择出子孔径样本后通过对各个子孔径中各距离向能量计算筛选出前能量最高的距离向单元。此步骤的子孔径分割示意图如图1所示。

图1 WML-PGA子孔径分割示意图
1.3 循环移位
对选择出的×个距离向长度为的距离向单元补偿初始相位后计算频谱最强幅度点索引,并将其循环移位至0频位置,从而避免最强幅度点相位对相位误差梯度估计的影响。
1.4 加窗滤波
通过对循环移位后的信号进行加窗置0,实现对杂波能量的滤除,提升信号的信杂比。
1.5 权值计算
同传统PGA不同的是,WML-PGA为了进一步提升相位梯度估计的准确性,通过对不同距离向的平坦度权值进行计算,在同一距离单元内相干积累时,平坦度权值高的样本将提升其在相干积累时候的影响,平坦度权值低的样本将减少其在相干积累的影响。该权值的引入有效提升相位误差估计的收敛速度与精度。

(3)

(4)
1.6 相位估计与拟合
该步骤利用了傅里叶变换的导数特性,即当()和()是一对傅里叶变换,表示为{()}=(),则如式(5)所示。

(5)
在估计出相位误差梯度后,对其进行积分便能够得到相位误差,并通过拟合滤除其中线性相位。
对以上步骤进行迭代,缩小步骤1.4所加窗的大小直至相位估计收敛。
2 PGA算法GPU并行化分析与实现
考虑到机载雷达成像系统对于系统功耗、尺寸、运算能力的要求,本文所选平台为NVIDIA嵌入式Jetson TX2平台。该平台拥有6个CPU核心和一个GPU。其中CPU包括四核ARM Cortex-A57和双核Denver2处理器,通过对6个CPU不同规模的使用,最大限度的满足不同场景下对嵌入式芯片的性能与功耗平衡,能够实现最低功耗7.5 W。该平台中GPU具有256个CUDA核心,DDR3内存达到8 GB。
2.1 内存分配的优化
当利用GPU进行运算的并行化时,往往需要将数据从CPU端通过PCIE发送至GPU内存当中,该操作不仅需要在CPU与GPU两端同时开辟内存,同时数据的传输速率将受到PCIE速率的限制。因此会带来内存与性能的双重消耗。本文针对WML-PGA算法实现过程中大规模数据的调用,基于TX2的CPU与GPU内存共享的特性,采用zero-copy技术,通过页锁定内存的HostAlloc分配方式达到规避数据拷贝的同时节省了内存。同时因为TX2的CPU与GPU内存共享的特性避免了数据的传输所带来的系统耗时。打破了GPU开发过程中PCIE速率对系统性能的限制。
2.2 库函数的使用
PGA算法中需要完成多距离单元与多子孔径个数的信号傅里叶变换,多次调用傅里叶变换的操作可以通过调用cuFFT库中的cufftPlanMany实现多个信号的傅里叶变换并行化运算。同时针对在计算均值时多向量点乘累加求和的计算需求,调用cuBlas库中的矩阵乘法函数cublasCgemm实现矩阵点乘累加求和的并行加速。
2.3 WML-PGA算法关键部分并行化分析
由WML-PGA算法原理可知样本选择会将雷达成像方位向数据分为个子孔径,同时根据各子孔径距离向能量大小选出能量前的距离向,具体子孔径分割示意如图1所示。考虑到该算法在样本选择后的运算均是以子孔径为运算单元,因此WML-PGA算法的并行化首先考虑利用在样本选择后实行各子孔径的粗并行,即在GPU中调用多线程对WML-PGA算法样本选择后的运算以多子孔径为并行运算。
对于样本选择后的运算,在子孔径中多次用到:多复数向量的点乘运算、转置、矩阵各行最大值索引、多信号方差、均值等运算操作。这些大规模数据运算将通过借助共享内存、多线程等手段对子孔径内运算进行细并行化。由上WML-PGA算法步骤1.3中系统需要完成×次长度为子孔径的频谱最大值索引位置计算。因此可以将该运算等价为行长度为×列长度为的矩阵各行最大值索引值的计算。
考虑到GPU的共享内存访问速度相比全局内存要快的多,开始作者提出利用共享内存加规约算法实现矩阵最大值索引的并行加速,具体做法为:将单个长度为的向量传进共享内存中,并设块中线程数为,共计×个线程块,借助同一块中的线程能够实现共享内存之间的通信这一特性,利用规约算法计算对长度为的向量最大值索引。但该做法受到以下三点约束:当PGA算法中的过大时,无法将长度为的数据全部导入共享内存当中;Tx2硬件限制了单个块中的线程总数无法超过1024,当大于1024时,单个块中的线程数将无法满足规约计算的使用;规约运算时,随着每次迭代,将会使相比于上次迭代中线程量一半的线程闲置,造成函数并行化效率不高。基于以上三点,本文提出将共享内存大小固定为32,将单个块的线程数设为32,具体线程分配示意如图2所示,同时只将各数据的前32个点存入共享内存当中,之后调用块中所有线程将存入共享内存的数据同未存入的数据进行比对,最终将长度为的数据中最大的32个数据与索引位置存入共享内存中,接下来再利用规约算法,在剩余的32个数据中迭代算出最大值与其索引位置。该做法使得函数不会受到子孔径数据长度的限制,同时单个线程进行了多次运算,减少了线程的浪费,提升了函数实现的效率。

图2 矩阵各行最大值索引运算线程分配示意图
3 试验结果与分析
3.1 cufft库函数的性能实验
因PGA算法中涉及多次傅里叶变换,针对Tx2与TMS320C6678两种不同平台上较大数据量的多信号傅里叶变换性能进行了实验统计。同时为了验证本文所提利用HostAlloc进行GPU内存分配避免内存搬移开销的可行性,对cudaMalloc、HostAlloc两种不同GPU内存分配方式下cufft库函数的耗时,以及在cudaMalloc分配方式时利用cuMemcpy进行内存搬移时的耗时进行了实验统计。其中为傅里叶变换的长度;为傅里叶变换的个数。即当=64,=64时,代表本次实验是同时实现64次64点FFT运算。
Tx2平台单次实验统计十万次后取平均耗时如表1所示。

表1 Tx2平台cufft性能统计
TMS320C6678的8核FFT性能统计如表2所示。
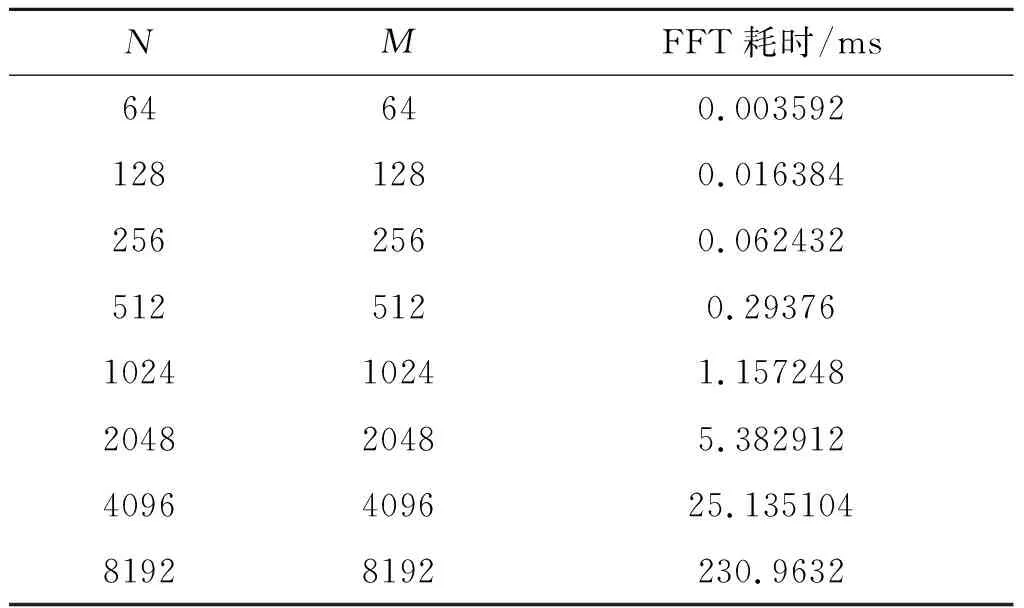
表2 DSP 6678的FFT性能统计
通过实验发现GPU在实现傅里叶变换时,加速比随着数据量的提升而增长。由表1可知,Tx2在实现8192×8192的FFT运算耗时40 ms,而6678在8192×8192的耗时为230 ms,加速比5.75。同时针对Tx2的CPU与GPU内存搬移函数耗时统计可以看出,当从CPU内存搬移8192×8192的数据至GPU内存当中,共计耗时约205 ms,而本文所提利用Tx2的HostAlloc内存共享特性避免了CPU与GPU内存之间的交换耗时,并且由图3可以看出HostAlloc与cuMalloc两种不同内存分配方式之间的运算耗时并无差异,证明了利用zero Copy避免数据搬移的开销同时未影响GPU处理的性能。

图3 Tx2、TMS320C6678的FFT性能比较
3.2 基于GPU的WML-PGA算法性能实验
利用GPU对PGA算法进行并行化加速,首先对本文所提技术的准确性同Matlab结果进行了比对,由下两幅图可知,本文所提技术实现了同Matlab估计结果10×10级别的估计误差,可以证明本文所提技术同Matlab实现的一致性。

图4 GPU与Matlab相位误差估计对比

图5 GPU与Matlab相位自聚焦估计误差
在对其准确性验证后,将本文所提技术同基于八核DSP 6678的PGA性能进行对比实验。分别对数据尺寸为8k×8k、8k×16k、8k×32k进行了性能对比实验。单组数据一万次运算统计取平均得到如表3所示。可以看出Tx2平台对PGA算法在数据尺寸为8k×32k时的加速比达到了4.82,同时可以发现当处理数据规模越大时,加速比越明显。证明本文所提技术相比于传统DSP平台的性能优势明显。
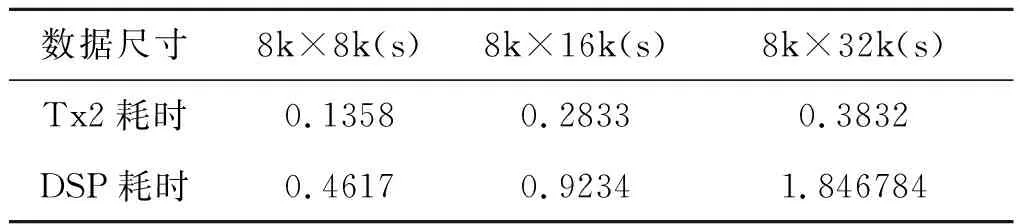
表3 Tx2、TMS320C6678的PGA处理时间统计
4 结束语
基于GPU的信号处理在近些年已经成为趋势,利用GPU的并行化处理将更好提升雷达成像算法处理的实时性。本文所提技术通过对比实验证明相比于传统TMS320C6678平台而言,最大加速比达到了4.82。同时Tx2功耗与TMS320C6678功耗均在8W左右。本文所提技术对雷达成像算法在嵌入式GPU平台的应用奠定了基础。
但受限于WML-PGA算法中运算步骤过多,所提技术更多基于数据的粗并行实现,该算法并行化加速仍然有很大的性能提升空间。同时Tx2平台的内存及性能均有提升空间,随着硬件的发展,更高性能的硬件投入使用后,本文所提技术性能将进一步提升。

