关联目标几何特征的激光引信探测距离统计分析方法

张凤萍,袁 伟,2,姜 毅,2,陆长平,2,章撼中

（1.上海无线电设备研究所,上海 201109;2.上海目标识别与环境感知工程技术研究中心,上海 201109）

0 引言

激光近炸引信具有探测精度高、抗干扰能力强等特点,被广泛应用在现代精确制导武器系统中。激光近炸引信一般由激光发射器发射光束照射目标,光束经漫反射进入激光接收器,再利用测量的目标距离信息估计目标几何特征,完成导弹的定距起爆。不论是空空导弹,还是空地导弹,在与目标交会时,交会姿态往往是不确定的。为了实现炸点的精确控制,激光近炸引信必须快速识别目标,完成精确定位。而为了配合弹药的引战延时起爆,激光引信只能利用目标的局部特征或边缘特征进行目标识别。为了提高激光引信的目标识别概率,往往需要设计一个较好的光束布局方式。

针对激光近炸引信可利用的目标信息有局限,需进行光束布局优化的问题,本文提出一种关联目标几何特征的探测距离统计分析方法。研究特定脱靶量和脱靶方位角条件下,攻击偏角和飞行落角对激光引信目标探测距离的影响,通过分析距离统计结果,给出光束扫描到目标边缘时探测距离的统计特征,并确定关联目标尺寸的理想光束宽度。

1 弹目交会模型的建立

为了完成激光引信对目标的探测距离统计,首先要建立弹目交会模型。该模型应能准确反映目标与导弹的相对运动及不同交会姿态下的弹目相对位置信息。将弹体俯仰角、攻击偏角、脱靶方位角等作为运动模型的输入变量。目标模型根据探测需求设置,应准确反映目标的尺寸,并简化为三维立方体模型。激光探测模型由单光束直线收发模型组成,不考虑探测光束功率损耗,默认测距精度满足测量要求。

以大地坐标系为参考,建立目标坐标系oxyz,其中z轴垂直地面,xoy面为水平面。以导弹质心为坐标原点o′,建立弹体坐标系o′x′y′z′,其中沿弹轴指向弹头方向为x′轴正方向,弹体纵向对称面内,垂直于x′轴、指向弹体顶部方向为y′轴正方向,z′轴垂直于弹体纵向对称面,与x′轴、y′轴组成右手直角坐标系。激光引信弹目交会模型示意如图1所示。地面目标以车为例,考虑真实目标尺寸,将其简化为一个8 m×6 m×6 m的三维立方体。靶中心放置在坐标点（0,0,6）位置处。

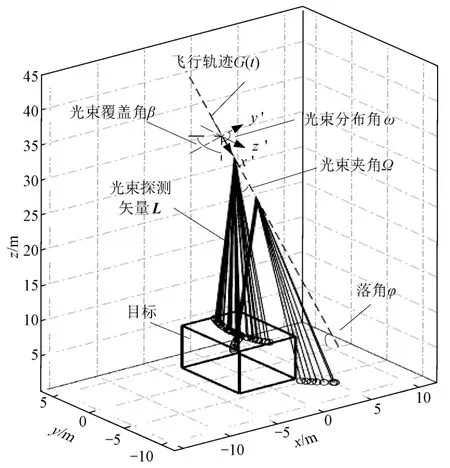
图1 激光引信弹目交会模型示意图

建立的导弹飞行轨迹模型G（t）与脱靶量λ、脱靶方位角θ、导弹攻向目标正面的偏角（简称攻击偏角）φ、导弹飞行落角φ及导弹飞行速度v有关。设v为导弹飞行速度在xoy水平面上的分量,v为导弹飞行速度在z轴方向上的分量。导弹飞行过程中,光束探测矢量L与弹轴的夹角（简称光束夹角）Ω保持不变。ω为光束分布角,即光束在弹体坐标系y′o′z′平面上的投影与y′轴正半轴的夹角。以导弹质心为光束出射点,激光光束的收发方向沿同一条直线。受飞行过程中导弹滚动角影响,单光束的探测可覆盖一定角度范围。光束探测矢量覆盖角度,即光束覆盖角β,根据实际应用情况取值。

激光引信探测器安装后,激光光束出射方向与弹轴位置一般相对固定,光束探测矢量L在弹体坐标系下的表达式为

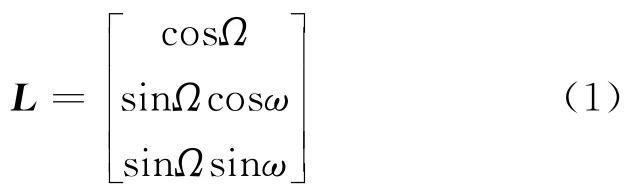
当Ω为60°,ω为180°时,导弹以弹轴为中心在-60°～+60°范围内滚动,则在导弹飞行过程中激光探测光束随机分布在120°范围内。为了消除滚动角对探测距离和激光光束落点的影响,将单光束探测矢量等效为光束覆盖角为β的多光束探测集。

2 探测距离统计分析模型

导弹飞行轨迹受脱靶量、脱靶方位角及飞行速度约束。飞行速度矢量方向主要受落角影响,而脱靶量和脱靶方位角主要决定了激光光束扫过目标表面的方位信息。为了研究激光引信探测距离与目标尺寸的关联性,需要基于激光引信弹目交会模型,建立输入变量随机分布的探测距离统计分析模型。

探测距离统计分析模型将脱靶量、脱靶方位角及飞行速度作为输入,攻击偏角φ和飞行落角φ在一定范围内随机取值。为了研究特定脱靶量和脱靶方位角条件下,攻击偏角φ和飞行落角φ对光束探测距离的影响,进行距离统计分析。通过分析距离统计结果,给出光束扫描到目标边缘时光束探测距离的统计特征,确定关联目标尺寸的理想光束宽度。

探测距离统计分析模型算法实现流程如图2所示。设置模型仿真参数,攻击偏角φ和飞行落角φ在参数范围内随机取值。每个探测距离S下重复N次随机姿态模拟,完成数据的统计。

图2 探测距离统计分析模型算法实现流程图

3 统计结果分析

3.1 统计结果

对探测距离统计分析模型中的脱靶量λ、脱靶方位角θ、光束夹角Ω、光束覆盖角β、导弹飞行速度v、光束探测距离S、攻击偏角φ、飞行落角φ等参数进行设置,如表1所示。其中光束探测距离S以1 m步进在（1～25）m范围内依次取值。每一个探测距离下,攻击偏角φ在-90°～+90°范围内随机取值,飞行落角φ在10°～80°范围内随机取值。

表1 探测距离统计分析模型参数设置

在每一探测距离下重复进行100次弹目交会仿真模拟,完成探测距离信息的统计。脱靶量为8 m时,激光光束探测到目标的概率P及探测到目标的最大有效光束宽度B的统计结果如表2所示。

表2 脱靶量8 m条件下统计结果

从表2可以看出:在探测距离大于18 m时,激光光束探测不到目标;探测距离小于等于18 m时,激光光束能够探测目标的最大光束宽度为70°。

3.2 最远特征点处探测距离

光束探测距离与目标照射点的相对关系如图3所示。

图3 光束探测距离与目标照射点关系示意图

假设弹轴方向与飞行方向不存在偏角,则探测光束与飞行方向的夹角为Ω′。某时刻探测光束刚好探测到目标表面距离目标靶中心点O最远的特征点N,设两点间的距离为S,明显此时脱靶量λ最大。当N点与导弹飞行轨迹的距离h最大时,光束探测距离S最远。则激光光束能够探测到目标的最远探测距离S的计算公式为

当λ为8 m,h为15.8 m,S为7.8 m时,根据式（2）计算得到最远探测距离S为18 m。即在探测距离S大于18 m时,探测光束均落在地面,无法探测到目标,与表2中的统计结果一致。

在探测目标尺寸确定并且脱靶量一定的前提下,不论脱靶方位角如何改变,均满足靶中心O到导弹飞行轨迹最短距离为脱靶量λ的约束条件。保持弹轴与飞行方向一致,在光束与飞行方向的夹角Ω′保持不变的前提下,通过调整脱靶方位角θ、攻击偏角φ和飞行落角φ,可以使得光束刚好探测到距离目标靶中心最远的特征点N,并且特征点N与靶中心O在飞行方向的同一垂直线上。探测目标最远特征点的几何关系示意如图4所示。设脱靶方位角θ为0°、攻击偏角φ为-48.531°、飞行落角φ为29.92°,根据图4计算得到的最远探测距离为18 m,与理论计算结果基本一致。

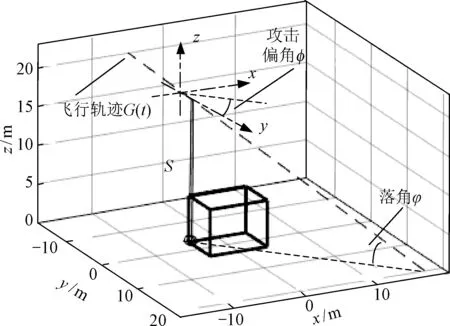
图4 探测目标最远特征点的几何关系示意图

3.3 目标尺寸与探测光束宽度

利用探测距离统计分析模型进行弹目交会模拟。当探测距离为某一固定值时,对飞行轨迹上不同位置处光束宽度为β的光束集的探测距离进行计算。只有当某一光束探测距离满足要求并且未照射到地面上（即照射到目标表面）时,判定该探测光束有效。

统计结果表明,针对尺寸为8 m×6 m×6 m的目标,在脱靶量λ为8 m、脱靶方位角θ为0°、攻击偏角φ变化范围为-90°～+90°、飞行落角φ变化范围为10°～80°的约束条件下,光束探测距离刚好等于脱靶量时,飞行轨迹上不同位置处的所有有效探测光束的光束分布角ω的分布范围最宽,为70°。

4 结论

本文通过建立激光引信弹目交会模型,在脱靶量、脱靶方位角、飞行速度、光束夹角和光束覆盖角固定,攻击偏角与飞行落角在一定范围内随机取值的条件下,对激光引信光束探测距离进行了统计分析。统计分析得到的最远探测距离与根据激光引信探测几何关系计算得到的目标最远特征点探测距离一致。统计结果表明:目标尺寸为8 m×6 m×6 m、脱靶量最大为8 m时,激光引信的距离探测能力不小于18 m;在脱靶量为8 m、脱靶方位角为0°时,有效探测光束的宽度最宽,为70°。因此在该弹目交会条件下,激光引信光束覆盖角应不小于70°,才能尽可能提高目标探测概率。