单孔主动预燃室火焰射流机理研究

费圣奕，王金秋，邓俊，刘逸晖，缪新轲，张智衡，李理光

（同济大学汽车学院，上海 201804）

随着我国汽车保有量的逐年上升，以及环境、能源问题的加剧，汽车工业面临着严重的碳排放控制和能源安全问题。传统内燃机遭遇节能与减排两大挑战，开发高效车用汽油机是实现中国汽车工业2030年碳达峰、2060年碳中和承诺的重要保障，具有重要战略意义。提高发动机的热效率，可以从泵气、燃烧、传热、排气等方面进行优化。对此，稀薄燃烧可以减少泵气损失、降低缸内燃烧温度、减少NO的排放，同时抑制爆震，从而提高发动机的理论热效率；但是稀薄燃烧也存在循环变动大、容易失火等缺陷，需要辅以新型点火方式来进行改善。

预燃室点火被认为是很有前景的一个技术路线，其可以缩短燃烧持续期，降低循环变动，非常适合与稀薄燃烧技术搭配来提高发动机的热效率。但就预燃室喷射特性，特别是射流贯穿距的研究较少，而其对燃烧系统设计有重要参考意义。有关喷孔喷射贯穿距的研究主要围绕喷雾特性开展。

对于直喷发动机喷雾特性的经验公式已经广受研究，如WAKURI等、NABER等基于动量理论与大量试验数据提出的柴油喷雾经验公式和PAYRI等、曾伟基于无量纲分析提出的汽油喷雾特性经验公式。然而经验公式本身存在着较大的局限性，不同经验公式的适用工况、燃油种类、喷嘴结构存在较大的差异。

预燃室与喷嘴不同的是，预燃室内部为非定常流动，其过程较为复杂，使用简单的定压燃烧、定容燃烧并不能很好地描述预燃室内的流动状态。为此，哈尔滨工程大学建立了预燃室内的双区模型，分为已燃区和未燃区。该模型中已燃区质量变化率可以通过层流火焰燃烧速度求得，而未燃区质量变化率为喷射质量变化率和已燃区质量变化率相加的相反数。然而，使用该模型建立的方程组无法直接求解，只能用Matlab进行迭代计算得到射流预测曲线，无法写成公式形式，在工程应用时较为繁琐。

GHOLAMISHEERI等通过快速压缩机试验测试了几种不同的喷口直径下的射流贯穿距随时间的变化关系。在喷孔附近，贯穿距和时间成正比；在远处，贯穿距和时间的0.5次方成正比。而在更远处由于射流碰壁，正比关系逐渐不存在，意味着射流贯穿距的经验公式为分段函数更为可靠，但GHOLAMISHEERI并未进一步总结出预燃室射流贯穿距的经验公式。

DESANTES等基于基本守恒方程，推导出自由湍流气体射流规律，建立了更通用的归一化参数，表征出了气体射流径向的质量和动量传递，并进行了试验验证。在此研究基础上，作者还建立了预燃室单孔喷口的射流贯穿距与发动机曲轴转角的关系式。ABANI针对预燃室贯穿距随时间长度的估计进行了推论，但DESANTES和ABANI所推导的公式均不为分段函数，对预燃室射流现象的描述不够充分。

本文基于圆形自由紊动射流的经验公式，提出了单喷口主动预燃室射流贯穿距的分段经验公式，并通过定容燃烧弹试验与Converge仿真验证，该公式拟合的射流贯穿距预测曲线与实测值较为一致。因此，可以认为该经验公式有较好的预测效果。对后续单喷孔预燃室结构的优化与设计起一定的指导作用。与传统的经验公式相比，该公式计算无需复杂的积分运算，只要知道喷口直径、射流在喷口处的初速度、射流锥角，就能预测出射流贯穿距曲线，但缺陷在于仅对单喷孔预燃室有效。此外，随着射流逐渐接近燃烧弹底部，燃烧弹已无法再被视为无限大的流体空间，受到流体边界层效应的影响，射流速度逐渐降低，无法再用公式获得准确的预测值。

1 试验装置

1.1 试验台架介绍

试验台架主要由定容燃烧弹、光学纹影系统、配气系统、排气系统和预燃室点火系统组成，如图1所示。试验所使用的定容燃烧弹如图2所示，该定容燃烧弹的常规耐压值为20 MPa，最高可承受1 000℃的高温，两侧有直径为80 mm的圆形光学窗口。光学纹影系统主要由LED光源、光学元件及高速摄像机等组成。采用Phantom v7.3型高速摄像机以256×256像素的分辨率和10 000幅/s的帧速进行拍摄。精密数字压力表安装于定容燃烧弹弹体上，用于在配气过程中确定燃烧弹内不同气体组分的分压，以配制不同过量空气系数（lambda）的混合气。其示数为相对压力，量程为0～2.1 MPa，精度为0.02% FS（Full Scale），满足试验中最高环境压力及精度的要求。试验中点火系统采用博世BS-0986AG0105型点火线圈实现升压，由Compact-RIO中 的FPGA（Field Programmable Gate Array）模块实现控制。台架中设置了同步触发电路，可通过计算机控制自动依次触发高速摄影机的录像功能、预燃室进气与火花塞点火，简化了试验操作，同时能准确记录点火时刻，计算火焰发展的时间。

图1 定容燃烧弹试验台架

图2 定容燃烧弹系统现场实物图

1.2 主动预燃室介绍

图3为课题组自主设计的主动预燃室结构示意图。该结构参考了SCHUMACHER等的设计思路，结构更为紧凑，其体积与M14×1.25 mm螺纹的火花塞接近，能够直接安装在未经改造的发动机缸盖上；预燃室上采用直径更小的火花塞和止回阀，更易于装配。该系统通过向预燃室内喷射少量纯甲烷气体，可以使预燃室内较稀薄的甲烷-空气混合气加浓。

图3 主动预燃室三维模型及其截面

1.3 试验过程及试验工况

用真空泵将定容燃烧弹气体抽出至弹内真空，随后向定容燃烧弹内充入0.2 MPa左右的干净空气，清洗燃烧弹内残余废气，再次将定容燃烧弹抽气至真空，随后向燃烧弹内充入=1.2的甲烷-空气混合气，弹内压力0.3 MPa，弹内温度27℃；预燃室甲烷喷射压力0.5 MPa，喷气脉宽4 ms。通过计算机控制预燃室进气，火花塞点火与高速摄影机的触发。重复该工况3次，以确保其可重复性。

2 仿真介绍

主动预燃室与燃烧弹的3维CFD（Computational Fluid Dynamics）仿真模型由CONVERGE软件建立，如图4所示。CONVERGE提供了几个物理和数值子模型。必须选择和修改适当的模型，以在模拟和测试结果之间达到可接受的一致性，同时平衡数字计算所需的时间资源。需要选择的模型有：湍流模型、燃烧模型、点火模型等。选择重整化群（Re-Normalization Group，RNG）-湍流模型。该湍流模型基于重整化群理论推导得到，对高速流动、旋涡流动有较好的精度，同时还考虑了低雷诺数的影响，在实际工程流动计算上具有较好的适应性。使用基于化学反应机理的SAGE燃烧模型。本次仿真使用的反应机理为GRI-MECH3.0提供的甲烷燃烧骨架反应机理，共包括53种组分和325个化学反应。采用火花塞间隙中的两级能量来模拟点火过程，每个阶段包含40 mJ的点火能量。CONVERGE在仿真过程中实时自动地生成笛卡尔网格，在建模过程中只要设置网格的生成规律即可。CONVERGE基于全局网格尺寸和局部网格加密级数来生成网格。局部网格尺寸跟全局网格尺寸的关系如式（1）所示。

图4 仿真模型3维示意图

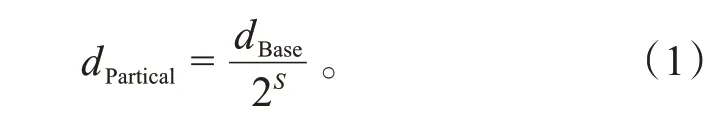
式中：为全局网格尺寸；为局部网格尺寸；为局部网格加密级数。

CONVEGE提供了网格自适应加密功能，能根据速度、温度、密度等参数的梯度自适应地在梯度大的地方加密网格。在本研究中，设定基础网格8 mm，对预燃室和主燃室开启自适应加密，加密级数分别为7级和3级。CONVERGE提供对指定区域的固定加密功能。本研究对预燃室整体设置3级加密；弹内射流发展区域设置2级加密；点火源设置5级球形加密区，同时采用更大直径的4级球形加密区作为过渡加密；预燃室主通道设置4级加密；预燃室喷口设置6级加密。固定加密区域如图5所示。

图5 主动预燃室燃烧弹模型网格的固定加密级数设置

需要指出的是：因为弹簧动力学和流体力学的耦合计算将使求解的数学模型变得十分复杂，此外，由于每次试验前均需将燃烧弹抽至真空，止回阀在预燃室一侧的压力会低于进气管内的压力，进而将进气管也抽至真空，因此实际进入预燃室的甲烷气体仅为所有喷气的一小部分。所以在建模时略去了预燃室的甲烷供给，直接设置预燃室内为lambda=0.9的甲烷-空气混合气。

除进气外，其余仿真条件均与试验工况一致，在后处理软件Tecplot中量取密度场射流的长度，如图6所示。

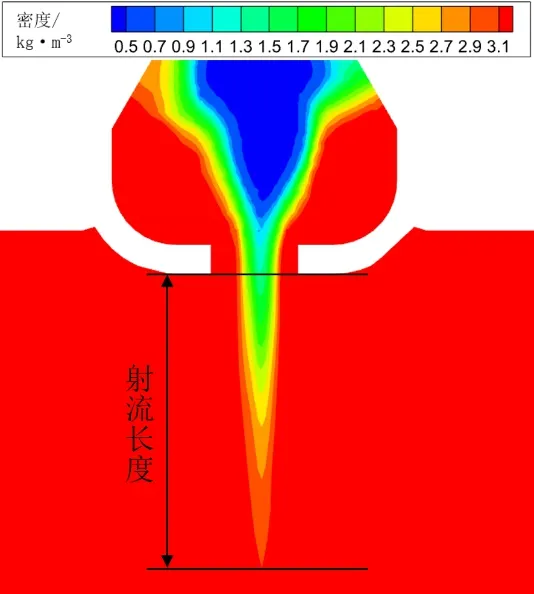
图6 仿真射流长度量取示意图

3 理论分析

若一股流体是从自小圆孔中射入流体特性相同的无限空间中，并且其流动状态为紊流，则可以称之为圆形自由紊动射流。对于单喷孔预燃室射流而言，火花点火后，预燃室内较浓的甲烷-空气混合气剧烈燃烧，紊流火焰以初始速度自预燃室喷口射入主燃室内，主燃室与预燃室内混合气具有相同的流动特性，与预燃室喷孔尺寸相比，主燃室可以视为无限空间。因此，单喷口预燃室射流可以简化为圆形自由紊动射流。

图7描述了圆形紊动射流模型的3段结构。射流以初速度自孔口出射后与周围静止流体间形成速度不连续的间断面，受到射流卷吸作用影响，把原来周围处于静止状态的流体卷吸到射流中，使射流边缘部分流速降低，难以保持原来的初始流速。

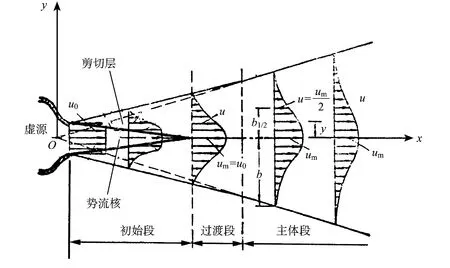
图7 自由紊动射流流动特征［16］

在射流初始段，由于周围静止流体与射流的掺混，无法影响到中心部分的射流核，所以中心部分射流速度u仍能保留初始速度，即：

在初始段，速度不变，射流轴向位移与时间成正比，即：

射流充分发展后，中心势流核受到周围流体的卷吸和掺混作用，无法继续保持初速度，为主体段。在初始段与主体段之间有一个很短的过渡段，一般在分析中不予考虑。在主体段内，射流速度u与射流轴向位移成反比，如式（4）所示。

式中：=/，为轴向位移；为射流在此位置的径向宽度，若把射流锥角定义为，=tan（/2）；为圆形开口尺寸。将式（4）写成微分方程的形式，即：

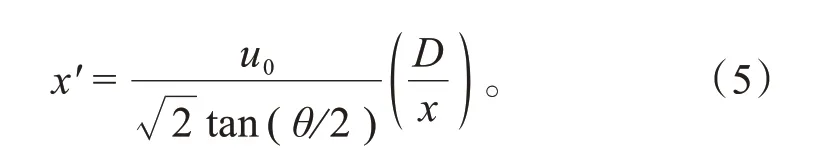
对微分方程求解可得主体段火焰射流与时间的关系式为：

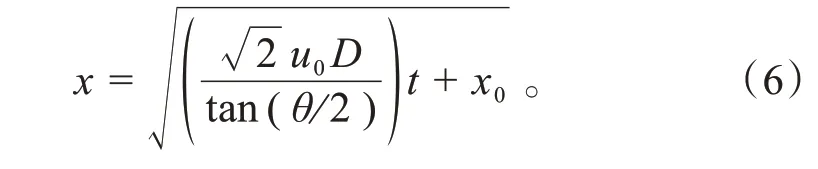
式中：为常数项。而主体段和初始段的分界点，可令式（4）中=，可以解得分界点到喷口的距离为：

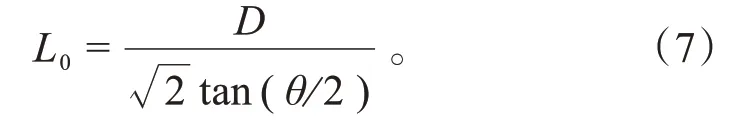
射流从喷口出发到分界点的时间为：

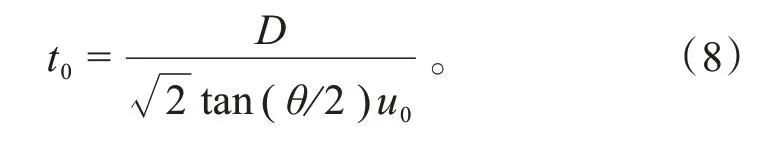
分界点前后位移相等，即式（4）与式（6）中的相等，得：

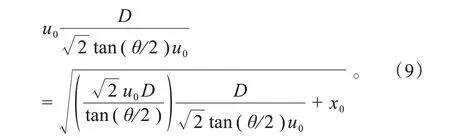
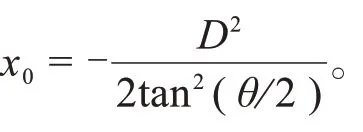
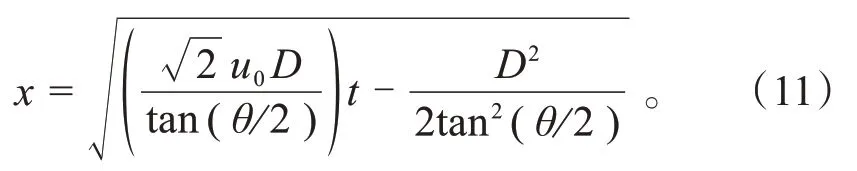
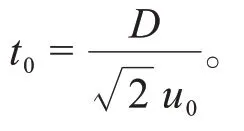
4 结果验证与分析

定义高速摄像机拍到射流的第1张画面为第1帧，对应时刻0.1 ms，此前一张画面为初始帧，对应时刻0 ms。=1.2工况下的主动预燃室燃烧弹试验的3组试验获得的射流长度如图8所示，分别记为试验A、B、C。射流锥角可通过在纹影上直接测量得到，射流锥角=28°，如图9所示。

图8 主动预燃室燃烧弹射流长度

图9 通过试验图像测量射流锥角示意图

预燃室喷口处的射流初速度无法通过试验直接测量。使用高速成像技术，可以测量射流长度，通过喷射行程距离Δ除以行程时间间隔Δ，可以计算得到高速摄像机拍到射流的第1帧与初始帧之间的平均速度ˉ，如式（12）所示。

式中：和分别为高速摄像机拍得初始帧和第1帧的射流长度，以试验A为例，=0 mm，=10.667 mm，Δ=0.1 ms。计算得到平均速度为106.67 m/s。如果假设求得的平均速度即为射流喷出时的初速度，即=ˉ=106.67 m/s，将计算得到的代入式（10）和式（11）。解得分界点=0.08 ms。以式（10）和式（11）预测的射流贯穿距曲线和试验A数据对比如图10所示。

图10 试验中Δt=0.1 ms计算的初速度所预测的射流长度曲线与实测值对比

发现以此方法求得的初速度用以预测射流贯穿距与试验实测值存在较大误差，最大误差为27.58%，这是因为受到高速摄像机帧率的限制。一方面，无法确定初始帧时刻射流尖端刚好处于喷口处，高速摄像机拍摄得到的第1帧并不能准确代表实际射流发展对应的0.1 ms时刻；另一方面，0.1 ms已位于公式分界点时刻0.08 ms之后，射流已进入主体段，相比于初始段，速度已有所衰弱，因此，计算得到的第1帧与初始帧之间的平均速度不能准确的代替喷口处的瞬时初速度，实际的初速度应该比图像计算得到的更大。

与试验相比，仿真输出结果的步长不受硬件限制，能够更加准确地获得射流在喷口处的初速度。当仿真步长与试验帧率相同，均为0.1 ms时，仿真与试验C结果对比如图11所示，仿真与试验C的最大相对误差为6.81%，平均相对误差为3.72%，可以认为仿真结果与试验一致，仿真能够代表试验工况下射流长度的真实发展情况，仿真所对应的初速度为真实值。通过减小仿真的步长为0.01 ms，计算得到射流在喷口处的瞬时速度为=189.23 m/s，以此初速度预测的射流贯穿距曲线如图12所示。预测值与实测值的平均相对误差为3.53%，最大相对误差为6.92%。认为式（10）和式（11）所预测的射流曲线能够准确地预测单喷孔主动预燃室的射流贯穿距。

图11 仿真与试验C结果对比图

图12 仿真中Δt=0.01 ms计算的初速度所预测的射流长度曲线与实测值对比

如果将试验获得的第1帧和第2帧的射流长度代入式（11），可得关于初速度和第1帧对应时间的二元一次方程组（13）。

式中：和分别为高速摄像机拍得第1帧和第2帧的射流长度，=3 mm，=28°。可以利用试验对应的、与公式解得的、，随后将计算得到的代入式（8）以求出分界点时刻，计算结果见表1。

表1 基于式（13）计算射流初速度u0

发现试验A、B的大于分界点，而试验C解得的小于分界点，说明试验C所对应的第1帧位于初始段。因此，将试验C的第1帧代入式（10），第2帧依然代入式（11）得到另外一组关于初速度和第1帧对应时间的二元一次方程组，如式（14）所示。

式中：和分别为试验C中高速摄像机拍得第1帧和第2帧的射流长度，=3 mm，=28°。

对试验C射流初速度的最终计算结果见表2，此时计算结果更为合理。通过对试验C射流初速度的计算，可以说明仅靠单个公式无法准确地描述射流贯穿距与初速度之间的关系。

表2 基于式（14）计算射流初速度u0

对于试验B和试验C而言，通过式（10）和式（11）计算得到的初速度与仿真得到的初速度=189.23 m/s相比，相对误差分别为0.50%和0.12%。但对于试验A而言，相对误差较大，为5.82%，仍在10%以内，可以接受。因此，认为通过将已知的射流长度与对应时刻代入式（10）和式（11）反向求得的射流在喷口处的初速度能够反映真实情况。

如果通过试验获得不同预燃室喷孔直径的射流贯穿距，以此求解初速度，可以寻求不同喷孔大小预燃室所能达到的最大喷口初速度，可以对后续预燃室结构的优化与设计，尤其是预燃室喷口孔径的优化与设计起一定的指导作用。

5 结论

（1）基于圆形自由紊流理论提出了单孔预燃室射流贯穿距与时间的经验公式。

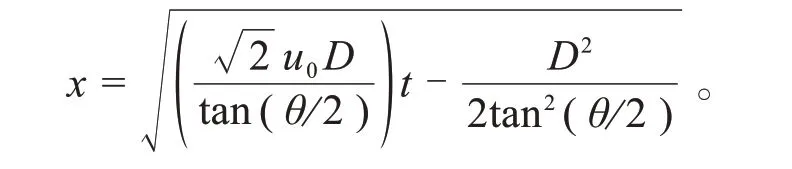
该公式可以通过射流锥角，预燃室喷口直径与射流从预燃室喷口喷出的初速度，预测射流长度。

（2）通过仿真分析，该经验公式能够较为准确地预测射流贯穿距，预测值与实测值的平均相对误差为3.53%，最大相对误差为6.92%（＜10%）。

（3）可以通过试验获得的射流贯穿距反向求解该射流对应的初速度。在相同工况下，以试验值反向求得的与仿真获得的真实值相比，最大相对误差为5.82%（＜10%）。

6 致谢

感谢国家自然科学基金（No.52076153）对本研究的资助；感谢慈溪市同鑫汽车零部件有限公司为本课题提供的样品加工支持。