拦截机动目标的分布式协同围捕制导方法
于江龙,董希旺,2,*,李清东,吕金虎,2,任章
1. 北京航空航天大学 自动化科学与电气工程学院飞行器控制一体化技术国防科技重点实验室,北京 100191 2. 北京航空航天大学 人工智能研究院,北京 100191
随着目标突防/隐身/逃逸能力的提升,无人机、智能飞行器等大机动目标威胁程度越来越大,单枚飞行器制导性能逐渐降低。多飞行器通过设备与功能差异配置,利用分布式信息交互提升探测与决策能力,凭借数量和策略优势,极大提升精确制导性能。协同制导方法在针对机动目标的防空和反导领域已取得丰硕成果。
协同制导方法已经有十余年的研究成果,从制导体系架构来看,协同制导架构一般可分为分层协同制导架构、分段协同制导架构以及领-从协同制导架构。分层协同制导架构是较早提出的一种架构,顶层是协同制导变量协调层,底层是协调变量执行层。文献[10]较早提出了这种架构,将剩余飞行时间作为协调变量,在底层采用攻击时间控制导引律。文献[10-11]将剩余飞行时间协调变量进行了修正,给出了改进攻击时间协同导引律。分段协同制导架构是将协同制导阶段分为两段或多段,在每段中协调不同的制导变量。文献[12]较早提出了这种架构,实现了攻击角度和攻击时间的同时保障。文献[13]利用两段式架构,实现了最优协同制导性能和攻击时间一致性的同时保障。文献[14]提出了一种带有辅助阶段的两段式架构,在攻击时间与攻击角度一致性保障的基础上,满足飞行器的过载/导引头视场约束。领-从协同制导架构借鉴了多智能体系统的一致性跟踪控制架构,通过多跟随者的协调变量跟踪领导者的协调变量,间接实现了制导协调变量的一致性。在这种制导架构中,领导者可以是真实的也可以是虚拟的,通过配置领导者的制导模式就可以配置整个多飞行器系统的协同制导性能。通过领导者与跟随者不同的协同制导形式,实现不同的协同制导任务,如多领导者协同定位,部分跟随者与领导者攻击时间一致、另一部分跟随者与领导者攻击角度一致等。因此,在这种架构下协同制导律设计更加灵活、方便,更具工程实际应用价值。
上述协同制导成果大多针对固定目标或者低速小机动目标。然而针对高速大机动目标,上述方法适用性并不是太好。针对大机动目标协同拦截问题,主要有4类方法:第1类是通过预测控制/轨迹预测方法,将机动目标协同制导问题转化为静止/低速目标协同制导问题;第2类是协同对策或协同博弈方法,从运动学层面给出协同制导律的解;第3类是采用滑模控制/自抗扰控制等手段,在协同制导律中设计偏置鲁棒项,补偿目标机动影响;还有一类是通过最优覆盖的策略,将多飞行器拦截域并集覆盖目标最大逃逸域,实现可靠协同拦截。
值得注意的是,上述方案能够在一定程度上实现对机动目标的拦截,但在初始阵位保障、协同制导可行性及制导参数求解实时性方面仍需进一步探索。多飞行器协同拦截机动目标问题,本质上是一个攻防博弈问题。在自然界中,狼群通过严密有序的组织及团结高效的协作,能够实现对羚羊、麋鹿等大机动猎物的有效围捕拦截。经过千百年进化,协同围捕这种行为在对抗非合作目标问题中是一种非常有效的手段。借鉴狼群围捕的行为学机理,文献[27-30]提出了狼群围捕算法,然而这类算法主要应用于协同决策和协同控制,在协同制导方面成果较少。狼群协同围捕猎物,本质是一个协同制导问题;狼群中有角色划分,围捕策略本质也是一个领-从协同策略。因此,通过深入研究狼群协同围捕的行为学机理,协同围捕策略应该且能够抽象为一种领-从模式协同围捕制导策略,这种协同围捕制导策略在多飞行器协同拦截机动目标问题中会具有广阔的应用前景。
本文借鉴狼群协同围捕机动猎物的行为学机理,研究了多-从模式下多飞行器协同拦截机动目标的协同围捕制导问题,提出了一套分布式协同围捕制导方法。与现有协同制导研究成果相比,本文的创新点主要有3点:① 借鉴狼群协同围捕机动猎物机理,提出了一套多领导者-多跟随者模式下的协同围捕制导框架。② 针对多领导者飞行器,设计了协同逆轨拦截制导律,为多跟随者飞行器提供有利的协同围捕拦截参考轨迹基准。③ 针 对多跟随者飞行器,设计了时变围捕视线角编队跟踪制导律,在目标逃逸方向两侧形成合适的围捕拦截构型。
1 多飞行器协同围捕制导问题描述
1.1 协同制导问题建模
考虑二维平面内枚速度不可控的导弹类飞行器对1枚机动目标的协同拦截问题,如图1所示。
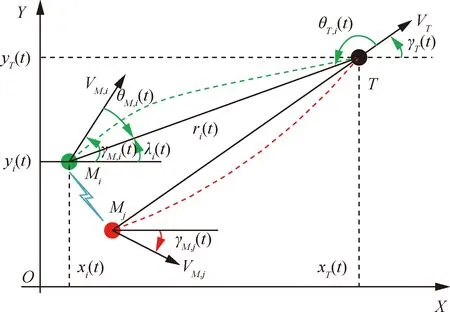
图1 弹目相对运动关系示意图Fig.1 Relative motion model sketch map
飞行器和目标的运动学模型表示为


(1)
式中:飞行器和目标的坐标为((),())和((),());,为飞行器的速度大小;为目标速度大小;,()和()为飞行器和目标的速度方向角。视线坐标系下相对运动学模型为

(2)
式中:()表示视线角;()为飞行器与目标之间的相对距离;,()和,()分别表示飞行器和目标的前置角。将式(2)转化为二维平面内的协同制导模型:
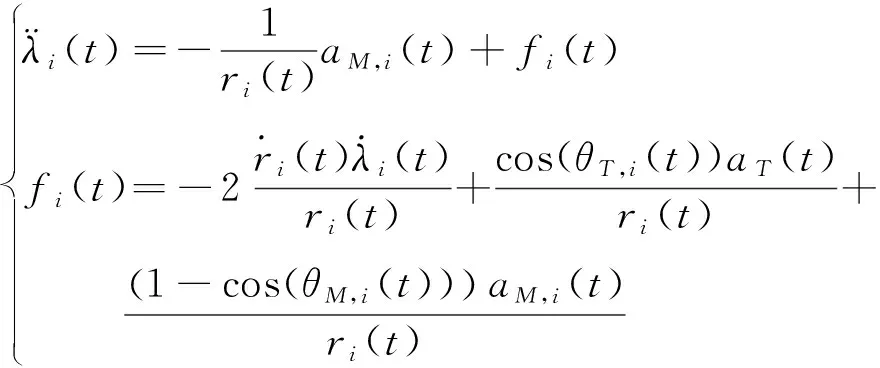
(3)
式中:,()和()分别为飞行器和目标垂直于视线方向的过载。
从制导模型形式来看,三维制导模型可以分成纵向和横向平面的制导模型,其相对运动学模型从形式上是一样的。因此从运动学层面,三维协同制导问题可转化为两个二维协同制导问题。
1.2 多飞行器分布式协同围捕制导策略建模
在自然界中,以狼群为代表的群体捕猎者,通过严密有序的组织及团结高效的协作,能够实现对羚羊、麋鹿等大机动猎物的有效围捕。协同围捕大机动猎物的策略经过千百年的进化,已经成为生物群体高级智能行为的典型代表。
狼群智能围捕行为与多飞行器协同拦截机动目标行为存在天然的表征与映射一致性。
狼群捕猎时,机动能力强的头狼(狼王或狼后)进行追逐、博弈与指挥,探狼则进行对猎物多方向协同探测。在本文中,具备指挥能力的头狼和具备探测能力的探狼,合称为领狼。从狼们则在领狼或邻居从狼的眼神、声音信息引导下,按照目标可能大机动逃逸的多方向进行多路围捕追逐。如果目标在领狼捕获能力范围内,则目标必然被捕;如果目标向某方向智能大机动逃逸且在领狼捕获能力之外,由于多从狼追捕时排成一个扇面、从各个方向包抄过去,则在目标逃逸方向上,必然存在尽管不是机动能力最强、但是阵位最优的从狼,以较小的机动、较平直的路线捕获目标,如图2所示。差异化配置、以数量换取阵位优势的合作捕猎,是一种高级的集群智能。
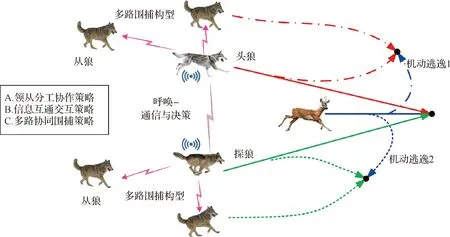
图2 狼群协同围捕机动猎物示意图Fig.2 Cooperative encirclement hunting of wolves
基于上述生物学行为学分析,狼群协同围捕大机动猎物的核心在于多领狼-多从狼角色分工(协调与配合)、领狼-从狼信息交互、狼群多路多方向协同围捕3类主要策略。从制导层面来讲,多飞行器协同拦截大机动目标和狼群协同围捕猎物的本质是一样的,就是实现对具有一定机动能力的目标的协同制导/拦截。因此,本文构想的分布式协同围捕制导方案的核心是借鉴狼群协同围捕策略,采用多领导者-多跟随者协同围捕拦截模式,高性能多领导者飞行器采取特定协同制导方式,一方面在拦截能力内实现对目标协同拦截,另一方面为多跟随者飞行器提供参考轨迹信息,以及目标信息与决策信息。针对多跟随者飞行器,一方面基于局部探测信息,采用分布式估计的方式获得领导者飞行器参考轨迹信息,另一方面构建合适的包围住目标的围捕编队构型,设计基于领导者参考轨迹的时变围捕编队跟踪制导律,保证使至少有一枚跟随者飞行器从合适的方向拦截机动目标。多枚拦截飞行器在目标逃逸方向上形成了一定散布的围捕构型覆盖,使得存在若干飞行器的末制导拦截阵位是合适的(初始航向误差小、拦截弹道平直、需用过载小),进而提高对目标的拦截能力与拦截成功率。下面针对分布式协同围捕制导方案中的3种核心策略进行数学映射建模。
1.2.1 多领导者-多跟随者飞行器协同围捕模式建模
假设枚飞行器中有-枚跟随者飞行器,及枚领导者飞行器(1<<-1)。枚领导者飞行器能够直接获得目标信息进行制导,-枚跟随者飞行器只能与领导者飞行器或邻居跟随者飞行器通信。枚飞行器之间的通信拓扑结构用有向图描述。令E={1,2,…,}表示领导者飞行器集合,F={+1,+2,…,}表示跟随者飞行器集合。
在本文的协同围捕制导策略中,考虑多领导者模式,即将具备指挥、决策和探测等能力的飞行器均归为领导者飞行器。多领导者模式具有较多优点,一方面能够免单领导者失效导致的拦截任务失利,另一方面能发挥多个高智能领导者之间的协同优势,能够为跟随者飞行器提供优化的参考轨迹,进而提高整个围捕拦截编队的作战效能。在性能配置方面,领导者飞行器为指控中心,主要携带高性能的探测、通信和计算设备,以及少量战斗部;跟随者飞行器为拦截策略的主要执行者,携带高性能战斗部,以及低性能的探测、通信和计算设备。
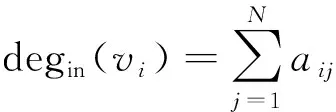
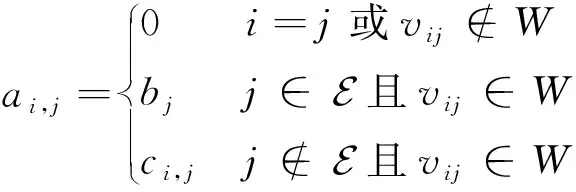
式中:>0,,>0。图的入度矩阵可表示为=diag{deg(),=1,2,…,}。如果对于任意的∈有∈,则称图为无向图,反之则称为有向图。如果有向图中的某个飞行器节点(根节点)均有一条有向路径能够到达另外所有飞行器节点,则称该图具有一个生成树。
如果飞行器不存在邻居飞行器,则称飞行器为领导者飞行器;如果飞行器存在至少一枚邻居飞行器,则称飞行器为跟随者飞行器。
如果飞行器的邻居不包含领导者飞行器,则称其为A类跟随者飞行器;如果飞行器的邻居包含所有领导者飞行器,则称其为B类跟随者飞行器;除此之外,在多枚领导者飞行器存在的情况下,如果飞行器的邻居仅包含一部分而非全部的领导者飞行器,则称其为C类跟随者飞行器。
多飞行器系统之间的拉普拉斯矩阵=-,且有:
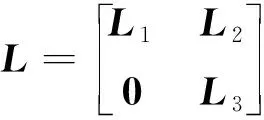
(4)
式中:∈×;∈×(-);∈(-)×(-)。
多飞行器系统的通信拓扑图是有向的;系统中不存在C类跟随者飞行器,至少有一枚B类跟随者飞行器,且系统具有以领导者飞行器为根节点的生成树。
根据假设1,则有以下性质:
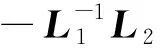
多领导者-多跟随者模式下的协同围捕策略可借鉴文献[31-33]中多智能体系统中的多领导者模式下的时变编队跟踪策略。在这种策略中,多跟随者受控状态以领导者受控状态组合参考轨迹为基准,形成特定时变编队构型。这种策略符合狼群围捕过程中的领狼指挥(提供基准)、从狼多路多方向围捕(特定时变构型拦截)的特点。因此多领导者模式下的时变编队跟踪策略将成为本文协同围捕制导的理论基础与方法架构。
1.2.2 分布式通信网络架构建模
为了利用局部信息实现分布式协同围捕制导,飞行器携带探测与通信设备是必要的。在本文中领导者飞行器发送信息给跟随者飞行器,跟随者飞行器能够接收邻居飞行器的信息。
飞行器与邻居飞行器+1之间的局部探测与信息交互如图3所示。
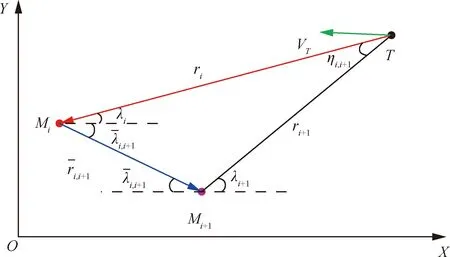
图3 飞行器之间的局部探测与信息交互示意图Fig.3 Local detection and information interaction of aircrafts
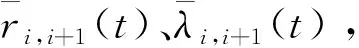
在假设2中,跟随者携带探测设备也是必要的。一方面跟随者飞行器可以探测到周围的威胁信息,满足飞行器之间的防碰要求以及与对障碍物的规避要求。另一方面,如果领导者飞行器失效,跟随者的探测设备能够在一定范围内为其提供目标信息,提高整个围捕拦截编队的生存与作战能力。通信设备可以传递飞行器之间的相对信息,也可以传递协同决策信息。
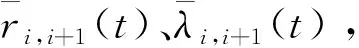
上述构建了多飞行器之间的分布式信息传输网络。通过该网络,多跟随者飞行器既可以获得对目标的制导信息,也可以通过下文分布式状态观测器获取领导者飞行器的状态轨迹信息。

1.2.3 多飞行器多方向协同围捕拦截策略建模
在给出多路多方向协同围捕策略建模之前,给出下列假设和定义。
在一个成功的拦截过程中,飞行器的前置角可以被限制在|,()|∈[0,π2)。
目标的过载()是有界的,目标的状态也是有界的。
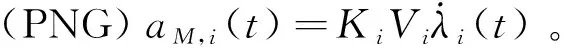
如果存在一个时刻,∈[0,,)使得∀∈[,,,)有|()-()|<π2成立,则称拦截过程为逆轨拦截,其中,()=()-π,,为拦截时刻。
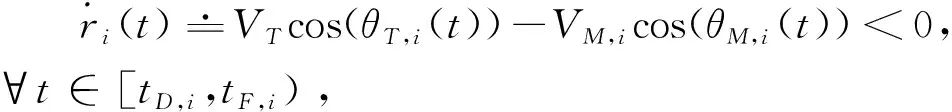
本节将基于领-从式时变编队跟踪控制方法来设计分布式协同围捕制导策略,在目标来袭方位的两侧布置拦截飞行器,使得至少有一枚飞行器能够从合适的角度实现对目标的拦截。本文的拦截模式为协同逆轨拦截,一方面能够减少拦截时间、缩小目标逃逸域;另一方面,当速度比小于等于1时,只能采用逆轨拦截模式。针对追击情况下的协同围捕制导问题,速度比应当大于1。以目标来袭方位为基准建立起协同逆轨拦截以及协同围捕拦截的态势,使得多枚飞行器从不同方向包围住目标,保证至少有一枚飞行器能够从合适的角度实现对目标的拦截。
多飞行器协同围捕制导策略主要解决两个问题。一个是如何选择状态变量来刻画协同围捕拦截行为,另一个是如何选择协同围捕拦截构型的基准。
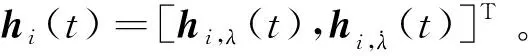
针对协同围捕拦截构型的基准选择问题,对多领导者飞行器选择目标速度方向角的补角()为基准,即多枚领导者飞行器在目标逃逸速度方向周围形成一定散布,形成协同逆轨拦截态势,以此对目标逃逸施加一定的压力。针对多跟随者飞行器,选择多领导者视线角轨迹的凸组合为基准,以此来刻画多跟随者飞行器均匀散布在多领导者“平均”轨迹两侧,保证存在某些跟随者飞行器(初始航向误差小、拦截过载小、拦截弹道平直的飞行器)能够有效拦截。在三维拦截情况下,可把时变围捕视线角编队函数,()扩展为二维向量,()=[,,(),,,()],形成一个空间排列问题。在实际工程应用中,一般采用二拦一或者三拦一的方式,由于三维协同制导纵向和横向平面的对称性,三维协同围捕制导下的耗弹量大概为二维制导两倍的数量级。
通过上述描述,多飞行器协同围捕制导中的领导者与跟随者策略可由下述定义描述:
如果条件式(5)满足,称领导者飞行器实现了协同逆轨拦截;如果条件式(6)满足,称多跟随者飞行器以多领导者视线轨迹凸组合为基准,实现了时变围捕视线角编队跟踪协同拦截。

(5)
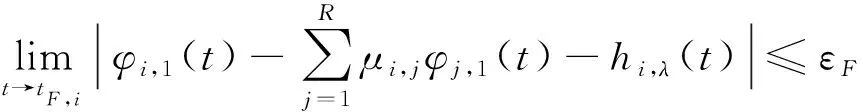
(6)

条件式(5)和式(6)可以由图4形象化表示。

图4 协同围捕拦截示意图Fig.4 Schematic of cooperative encirclement hunting interception
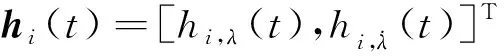
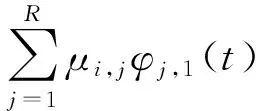
针对飞行器可用过载约束,可将其转化为期望的最优初始阵位约束(如文献[24-26]),或者本文刻画的最优时变视线角编队向量,(),最优,()的设计应当使多飞行器拦截可行域并集覆盖目标的逃逸区域,又能实现最小的拦截导弹数量。本文目前构建了一种可行的协同围捕制导方案,在未来研究中继续考虑过载约束受限下的最优时变视线角编队向量设计问题。与文献[24-26]不同,本文的方法能够实现异构协同制导功能,而且通过领导者之间的决策,也能够给出类似文献[24-26]中的最优初始阵位。本文的协同制导架构更加符合协同决策-制导一体化的特点基于这两种行为,给出下述协同围捕拦截的数学定义。
如果下面两个条件成立,则称多飞行器系统对机动目标实现了多领导者-多跟随者模式下的协同围捕拦截。
1) 飞行器的所有状态都是有界的。
2) 对于有界初始条件[,1(0),,2(0)],存在一个小的正数>0使得下述条件成立:
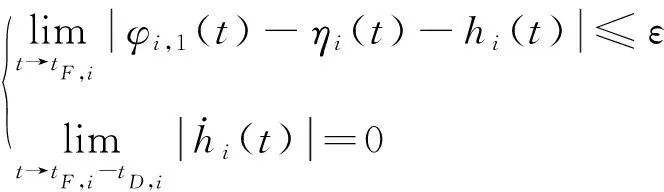
(7)
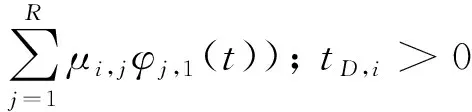
在给出多飞行器协同围捕拦截的问题描述之后,针对多飞行器系统式(1),本文主要解决以下两个问题:
1) 如何为多领导者和多跟随者飞行器分别设计协同逆轨拦击制导律,以及分布式时变围捕视线角编队跟踪制导律。
2) 如何分析闭环协同制导系统的稳定性,以及如何给出保障多飞行器系统式(1)对目标实现协同围捕拦截的条件。
2 多飞行器分布式协同围捕制导律设计
2.1 分布式协同围捕制导框架设计
采用分布式观测-独立跟踪控制的模式来构建分布式协同围捕制导律的框架,如图5所示。
在上述分布式协同围捕制导律框架中,多领导者飞行器在指控层面采用协同逆轨拦截制导律,压迫目标的逃逸区域,从而为多跟随者飞行器提供合适的参考轨迹。由于通信拓扑的约束,并非所有跟随者都能获得领导者的轨迹信息,因此采用分布式估计的方式获得领导者视线轨迹凸组合信息。多跟随者飞行器以此为基准,采用时变围捕视线角编队跟踪制导律,以此形成多路多方向协同围捕拦截。
在文献[27-29]中,学者们基于狼群围猎的思想,提出了“狼群围捕算法”、“围捕控制”等概念,来对相关研究方法的特点进行精准描述。本文从狼群的3种协同围猎策略中得到启发,提出的协同制导架构包含3种核心策略。为了刻画狼群智能围捕行为与本文协同制导架构的表征与映射一致性,称图5中的协同制导架构为协同围捕制导。本文提出的分布式协同围捕制导律框架具有一定的包容性,其他形式的协同制导律也可嵌入其中。对于多领导者飞行器,也可以采用协同定位制导律、协同博弈制导律或者协同探测制导律,进而可根据不同配置、不同任务需求,产生不同性能的参考轨迹。以参考轨迹的凸组合作为跟随者飞行器围捕拦截的基准,也可以根据实际任务需求设计其他参考基准。此外,对于跟随者飞行器,本文在视线坐标系下以视线角变量为围捕构型变量,也可采用惯性坐标系进行刻画围捕构型并设计相应的围捕制导律。
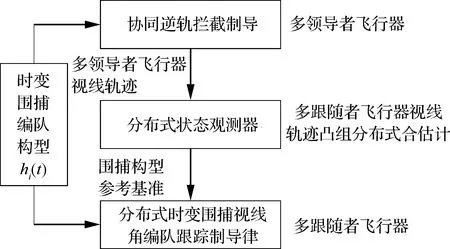
图5 分布式协同围捕制导律框架Fig.5 Distributed cooperative encirclement hunting guidance framework
2.2 多领导者飞行器协同逆轨拦截制导律设计


(8)
式中:
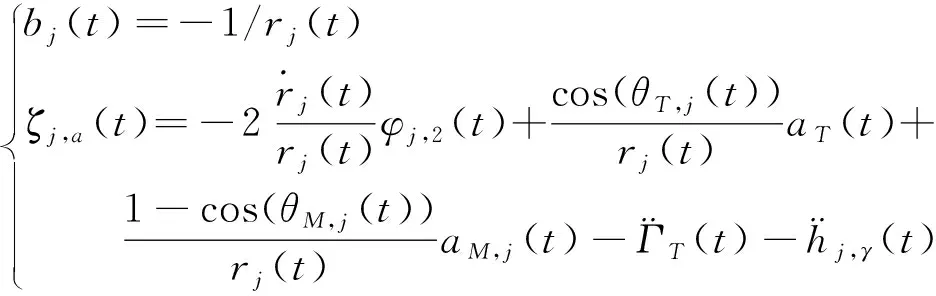
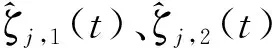

设计扩张状态观测器为
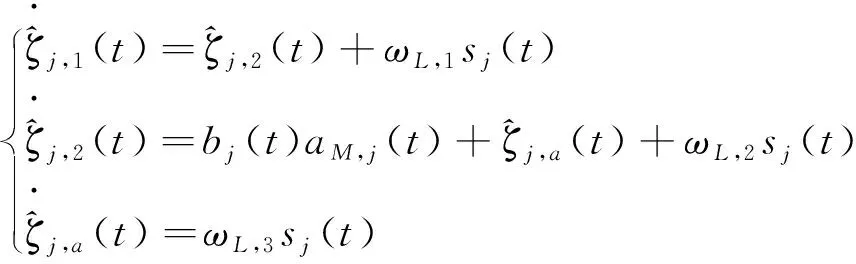
(9)
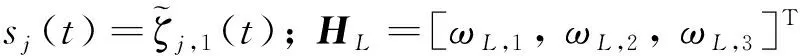
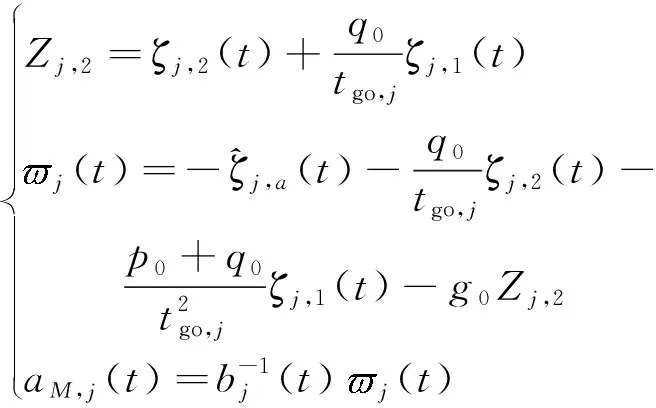
(10)
式中:,2()为中间变量;go,=,-为剩余飞行时间;>0、>0和>1为增益常数。
2.3 多领导者视线轨迹凸组合分布式估计
多跟随者飞行器在实现时变围捕视线角编队跟踪拦截的同时,需要对领导者的视线角轨迹凸组合进行跟踪,然而由于通信拓扑的限制,并不是所有跟随者都能够获得领导者的视线角轨迹。因此对多领导者的视线轨迹凸组合进行分布式估计。给出分布式有限时间状态观测器形式:


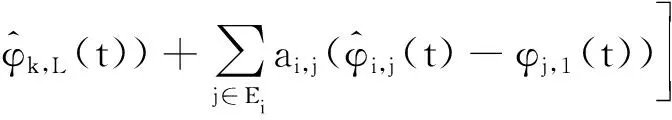
(11)
式中:>0; 0<<1。分布式有限时间状态观测器式(11)的稳定性以及有限时间收敛性在文献[36]中已给出。这里简要叙述,令
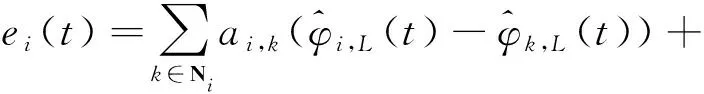
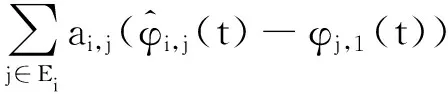
(12)
则有
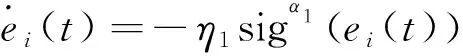
(13)
根据文献[36]可得()在有限时间内趋于0。令()=[+1(),+2(),…,()],则
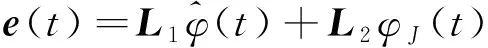
(14)
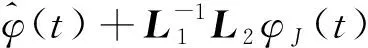
观测器式(11)给出的是多领导者飞行器视线轨迹信息,根据图1中视线角的定义,观测器的基准一般选择为惯性坐标系的轴。针对多飞行器协同制导,可将多枚飞行器的轴在射前装订成相同的,这样分布式通信和分布式观测器式(11) 就有了统一的基准。
2.4 多跟随者飞行器时变围捕视线角编队跟踪制导律设计
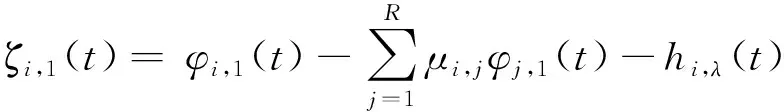
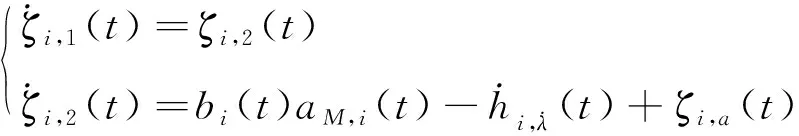
(15)
定义动态面()=,2()+,1(),因此有:
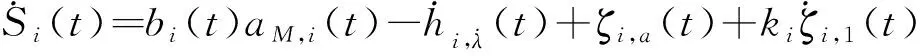
(16)
式中:
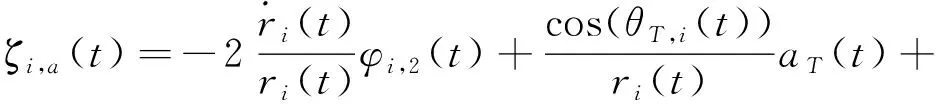
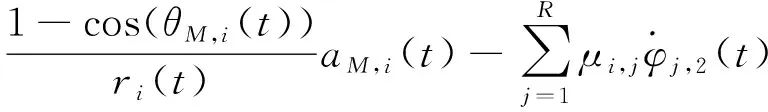
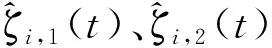

分布式扩张状态观测器设计为
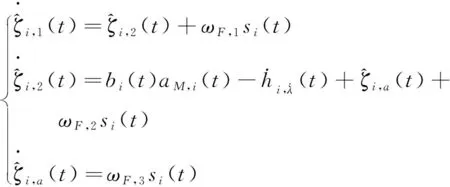
(17)

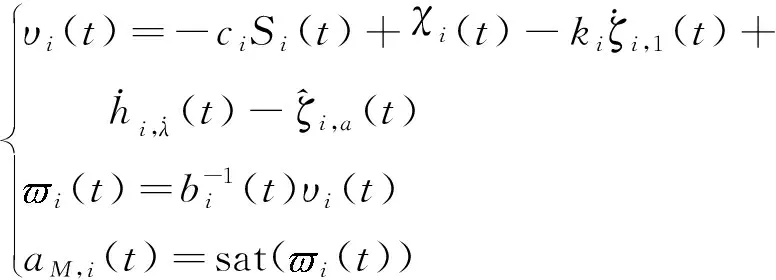
(18)


(19)

(20)

综上所述,多领导者协同逆轨拦截制导律式(10) 以及多跟随者的分布式有限时间状态观测器式(11)、时变围捕视线角编队跟踪制导律式(18) 合称为分布式协同围捕制导律。
在给出分布式协同围制导律的形式后,下面给出制导参数的设计方法。
为实现多飞行器对机动目标的协同围捕拦截,分布式协同围捕制导律、和的参数可由以下步骤给出。
针对设计的期望时变围捕编队(),检验以下时变围捕视线角编队跟踪可行性条件:

(21)
如果存在≥0使得式(21)成立,则继续设计协同围捕制导律;否则时变编队()将不满足要求。
选择合适的,1>0,,2>0。设计>0,>1,>0,>0, 0<<1。
求解下列线性矩阵不等式获得正定解>。
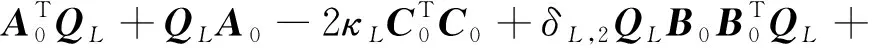
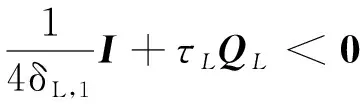
(22)
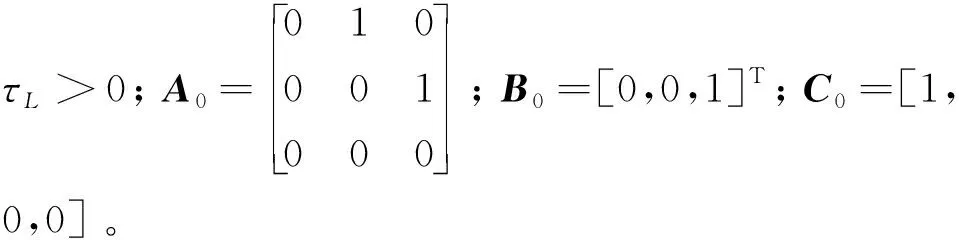


(23)
求解下列线性矩阵不等式获得正定解>。
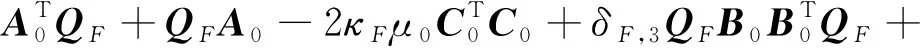

(24)
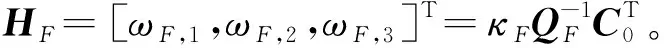
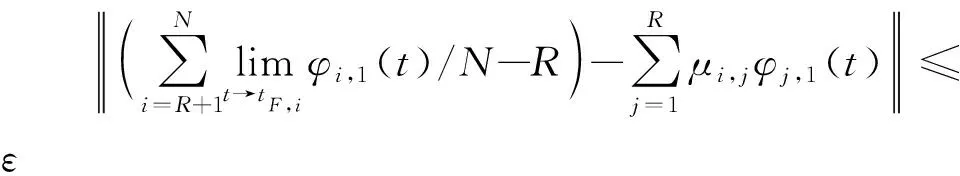
3 闭环系统稳定性与协同制导可行性分析
在给出分布式协同围捕制导律的设计方法后,本节将分析闭环系统的稳定性,给出保障多飞行器系统式(3)对目标实现协同围捕拦截的条件。
根据动态系统式(8)和式(9),可以得到观测误差动态系统:

(25)


(26)
根据式(15)和式(17),可得观测误差动态系统:

(27)


(28)
3.1 多领导者飞行器协同制导系统稳定性
如果多领导者飞行器的协同逆轨拦截制导律式(10)按照算法1中的步骤2、3设计,则多领导者飞行器在制导律式(10)作用下实现了对目标的协同逆轨拦截。
针对领导者飞行器,选择李雅普诺夫函数为,,1()=05(,1()go,)。注意:
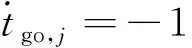
则将,,1()对时间求导可得:

(29)


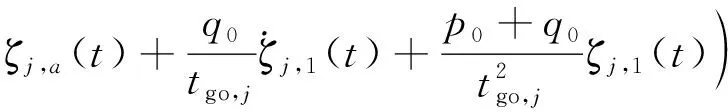
(30)
将制导律式(10)代入式(30)可以得到:
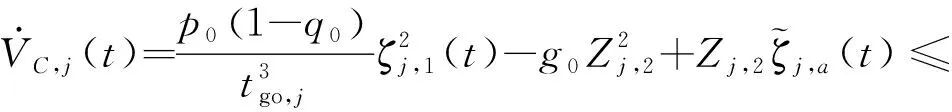
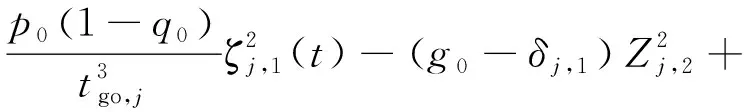

(31)
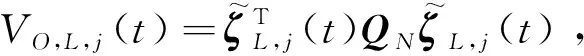
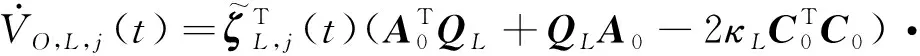
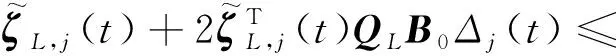
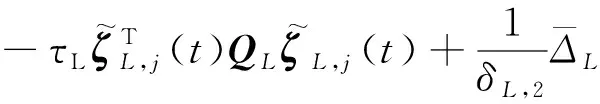
(32)
式中:,2>0。令,()=,,()+,,(),则根据式(31)以及式(32)可得:
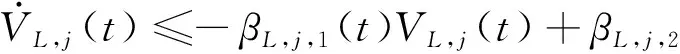
(33)
其中,

因此有
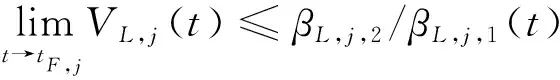
(34)
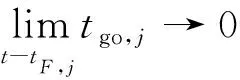
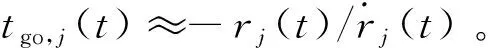

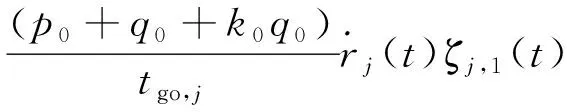
(35)
可以看出协同逆轨拦截制导律式(10)具有鲁棒偏置比例导引律的形式,在工程实现方面具有一定的实用性。
3.2 多跟随者飞行器协同制导系统稳定性
如果可行性条件式(21)成立,时变围捕视线角编队跟踪制导律式(18)按照算法1中的步骤4、5设计,则多跟随者飞行器在制导律式(18) 作用下实现了以多领导者视线轨迹凸组合为参考的时变围捕视线角编队跟踪协同拦截。



(36)
因此,将式(18)代入式(36)可得:

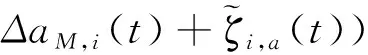
(37)
根据Young不等式,可以得到以下不等式:
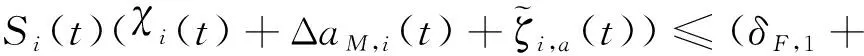

|()Δ,()|
(38)
式中:,1,,2>0。将式(38)代入式(37),可得:



|()Δ,()|
(39)

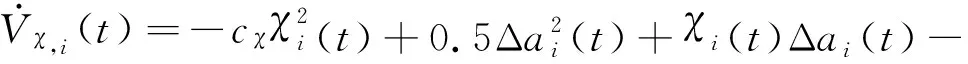
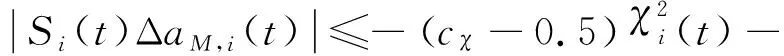
|()Δ,()|
(40)
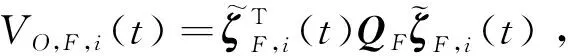

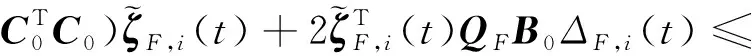

(41)
式中:,3>0。针对多跟随者飞行器,设计时变围捕视线角编队跟踪制导误差闭环系统李雅普诺夫函数,()=,,()+,()+,,(),有:
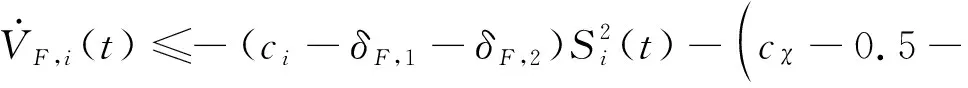
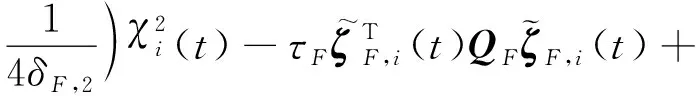

(42)
其中,

对微分不等式进行积分化简可得:

(43)
根据李雅普诺夫稳定性理论,不等式意味着,()一致有界的,同样,,()也是一致有界的。因此多跟随者飞行器在时变围捕视线角编队跟踪制导过程中的状态都是有界的。此外,根据,,()和()的定义,存在>0使得下述不等式成立。
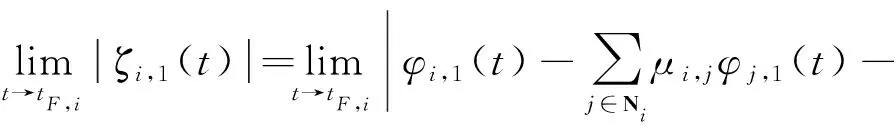

(44)
因此,条件式(6)成立。根据定义4,多跟随者飞行器实现了以领导者视线轨迹凸组合为参考的时变围捕视线角编队跟踪协同拦截。证毕。
3.3 协同制导可行性
在定理1和定理2的基础上,给出定理3以分析保障多飞行器系统式(3)对目标实现协同围捕拦截的条件。
如果时变围捕视线角编队跟踪可行性条件式(21)成立,分布式协同围捕制导律式(10)、式(11) 和式(18)按照算法1中的步骤2~5设计,则多飞行器系统在分布式协同围捕制导律的作用下实现了对机动目标的协同围捕拦截。
:由于分布式协同围捕制导律式(10)、式(11) 和式(18)是按照算法1中的步骤2~5设计的,而且可行性条件式(21)成立。则定理1和定理2成立。这意味着多领导者飞行器实现了对目标的协同逆轨拦截,多跟随者飞行器实现了以领导者视线轨迹凸组合为参考的时变围捕视线角编队跟踪协同拦截。从定理1和2可知,条件式(5) 和式(6)成立。
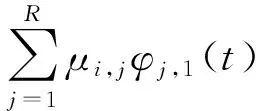
如果,>,,则领导者飞行器已经实现了对目标的拦截。则跟随者飞行器将不用继续对目标进行制导,或者去执行其他拦截任务,这不是本章的研究重点,在这里不详细阐述。因此对于∈F,定义5的条件2)满足。综上所述,定义5中的两个条件均满足,因此多飞行器系统在分布式协同围捕制导律的作用下实现了协同围捕拦截。证毕。
针对引导不同拦截飞行器进入协同制导所期望的拦截队形的问题,在中制导阶段,首先根据目标的当前位置,估计参考弹道(领导者飞行器)的预测命中点,通过构建合适的时变围捕视线角编队向量,(0)刻画跟随者飞行器的期望末制导初始阵位,即得到预测中末制导交班点。其次,采用模型预测规划、预测-校正等方式更新预测命中点与预测交班点。进而,采用带有飞行时间和进入角度约束的协同中制导律,引导不同拦截飞行器进入协同制导所期望的拦截队形。
协同围捕拦截成功性与飞行器的过载能力密切相关。在拦截的后期,如果领导者不能实现协同逆轨拦截,或者拦截失败、丢失目标,则跟随者飞行器在近距离内可以利用自身携带的低性能探测设备获得目标信息,切换为比例导引律实现继续制导。在这个时候,由于时变围捕视线角编队跟踪误差收敛至小的有界残集,对目标的围捕态势近乎形成(或者在目标的可能逃逸方向上均有拦截飞行器),因此不管目标向哪个方向逃逸,该方向存在若干合适的拦截飞行器(初始航向误差小、拦截过载小、拦截弹道平直的飞行器)。因此本文研究的协同围捕拦截策略优势之一在于降低飞行器的平均过载,降低目标逃逸概率,从而提高拦截的成功率。此外,由于飞行器从不同方位对目标实施拦截,不同的飞行器能够从不同的角度对目标观测,并且通过通信设备传递目标信息,因此协同围捕拦截策略优势之二在于增强整个拦截编队的探测效果。
4 仿真实验分析
本节将给出两个仿真实验,对分布式协同围捕制导理论结果的有效性进行验证。
考虑6枚飞行器协同围捕拦截一个机动目标。飞行器之间的通讯拓扑结构如图6所示。
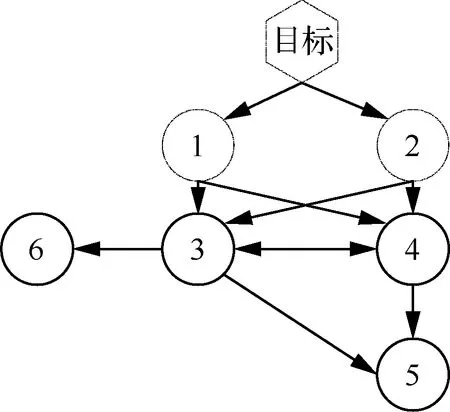
图6 通信拓扑结构图Fig.6 Communication interaction topology

4.1 标称状态多飞行器分布式协同围捕拦截仿真
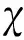

式中:=π20,=-25°,=25°,=-5°,=5°,1,,0=-4°,2,,0=5°,3,,0=-9°,4,,0=8°。

领导者飞行器对目标进行协同逆轨拦截的二维轨迹曲线如图7所示。领导者飞行器在拦截过程中的过载曲线如图8所示,可以看出过载是有界的。图9展示了拦截过程中的协同逆轨拦截误差,1()=,1()-()-,()曲线,在拦截时刻有,1(,)趋于小量,这也意味着条件式(5) 成立。两枚领导者飞行器的最终拦截脱靶量为0.4 m和0.35 m,这意味着多领导者飞行器对目标实现了协同逆轨拦截,也验证了本文提出的协同逆轨拦截作为一种准平行接近方法的有效性。
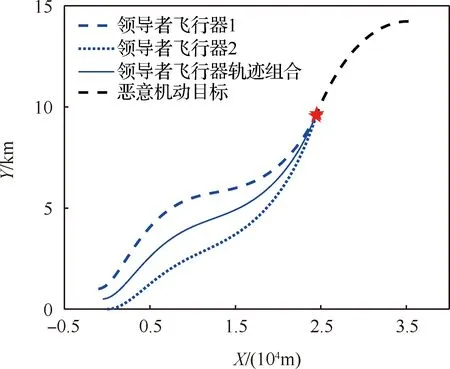
图7 领导者飞行器协同逆轨拦截目标的轨迹Fig.7 Cooperative head-on interception trajectories for two leader aircrafts
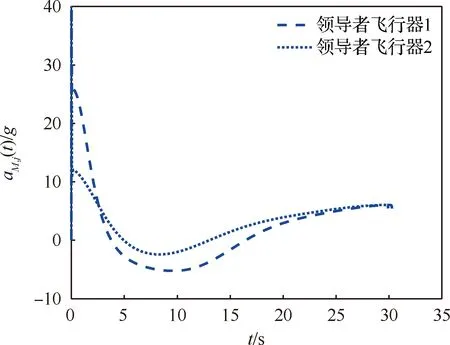
图8 领导者飞行器过载曲线Fig.8 Acceleration for two leader aircrafts
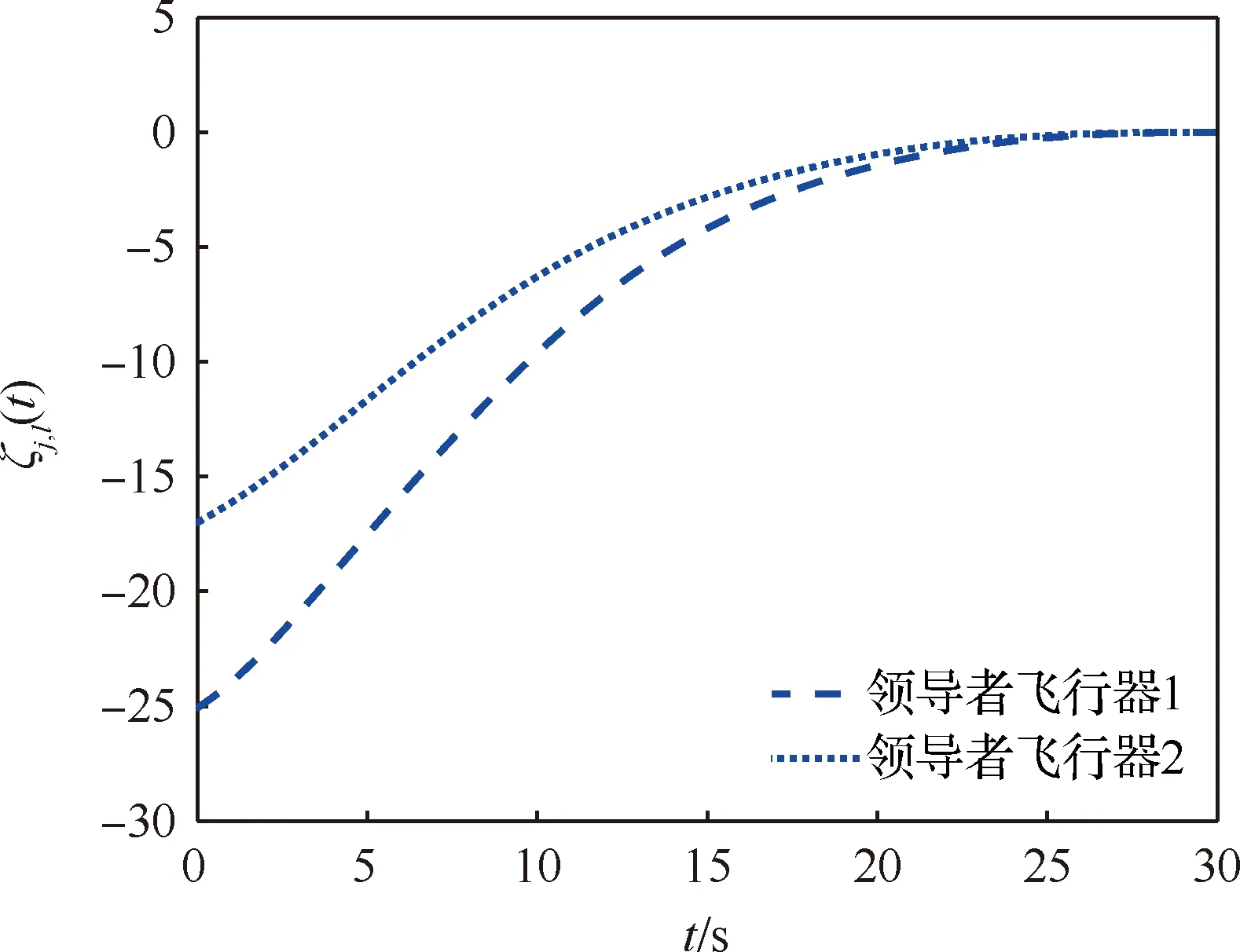
图9 领导者飞行器协同逆轨拦截误差曲线Fig.9 Head-on interception errors of two leader aircrafts
分布式状态观测器的性能如图10所示,可看出多跟随者能够对领导者状态轨迹凸组合有效估计。多跟随者飞行器对目标的时变围捕视线角编队跟踪拦截轨迹如图11所示。4枚跟随者飞行器在拦截过程中的过载曲线在图12中给出,可以看出过载均满足限幅。

图10 领导者视线轨迹凸组合及其分布式估计Fig.10 Line of sight angle trajectory convex combination and the distributed estimations of leader aircrafts
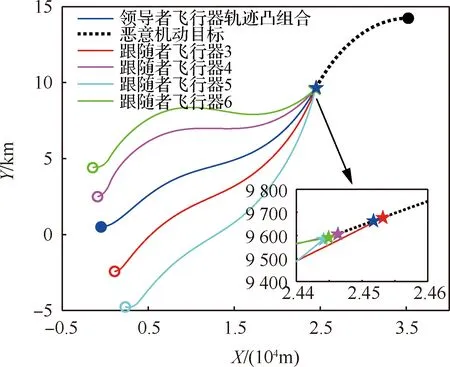
图11 多跟随者飞行器协同拦截机动目标轨迹曲线Fig.11 Cooperative interception trajectories against the target of follower aircrafts
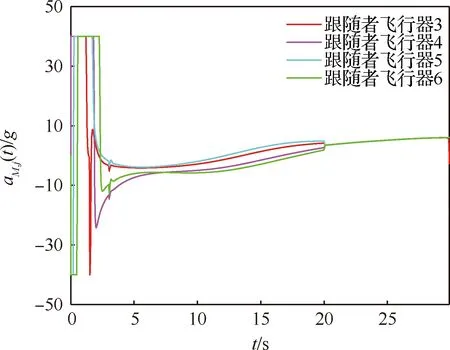
图12 多跟随者飞行器过载曲线Fig.12 Accelerations for follower aircrafts
动态补偿增益信号曲线在图13中给出,可看出补偿增益信号的幅值也是有界的,且随着过载不超过最大幅值,动态增益信号将趋于0。

图13 多跟随者飞行器的补偿增益信号Fig.13 Compensation signals for follower aircrafts
跟随者飞行器的视线角曲线,1()如图14所示,时变围捕视线角编队跟踪制导误差曲线如图15所示。由于跟踪制导误差,1()收敛一个小的残集内,因此条件式(6)成立,这也意味着多跟随者飞行器实现了以领导者视线轨迹为参考的时变围捕视线角编队跟踪协同拦截。多跟随者飞行器的脱靶量分别为0.31 m、0.23 m、0.21 m和0.15 m。综上所述,多飞行器系统在分布式协同围捕制导律的作用下实现了对机动目标的协同围捕拦截。

图14 多跟随者飞行器视线角曲线Fig.14 Line of sight angle trajectories for follower aircrafts

图15 多跟随者飞行器时变围捕视线角编队跟踪误差Fig.15 Time-varying encirclement hunting guidance error for follower aircrafts
为了分析不同初始进入条件对协同围捕制导效果的影响,设定不同的(0),以多跟随者飞行器时变围捕视线角编队跟踪初始误差,1(0)为自变量,给出协同围捕制导成功(每枚飞行器脱靶量小于0.5 m)的仿真结果,见表1。通过仿真看出,每枚飞行器大概有10°的初始进入条件。

表1 不同初始进入条件对协同围捕制导的效果

表2 不同噪声对协同围捕制导的效果
当目标做更加复杂的正弦机动时,设置目标持续机动过载为=11sin(02)。仿真结果如图16所示。根据仿真结果,多飞行器的脱靶量分别为0.21 m、0.22 m、0.35 m、0.32 m、0.23 m、0.22 m。因此,多飞行器通过采用协同围捕的方式,仍能够实现对正弦机动目标的有效拦截。

4.2 可用过载降低下的分布式协同围捕拦截仿真

仿真结果如图17和图18所示。在通过仿真发现在这种高动态环境下,6号跟随者飞行器由于初始航向误差小能够实现对目标的成功拦截(脱靶量为0.25 m),而3、5号飞行器则由于阵位不合适导致航向角误差较大,因此不能拦截成功。因此,本仿真算例也证明了通过在目标来袭方向两侧构建合适围捕拦截态势,使得在目标向某一个方向进行大机动逃逸时,该方向均有初始航向误差小的拦截飞行器,拦截弹道较为平直,过载需求较小,进而能够提高拦截的成功率。

图17 多跟随者飞行器协同拦截机动目标轨迹曲线Fig.17 Cooperative interception trajectories against the target for follower aircrafts

图18 围捕过程中飞行器的过载曲线Fig.18 Accelerations for six aircrafts
为了验证跟随者飞行器在低性能探测器工作时下的探测能力鲁棒性,令目标机动方式不变,多飞行器从不同的弹目距离切换成偏置比例导引律(低性能探测器给出制导指令),协同制导的效果如表3所示,可以看出多飞行器系统能够在相对距离7 km以上时仍能够实现对机动目标的有效拦截。

表3 低性能探测器工作时下的探测能力鲁棒性Table 3 Robustness with different detection capability
4.3 分布式协同围捕拦截与其他方法的对比仿真
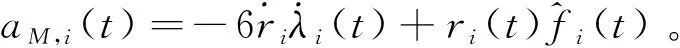
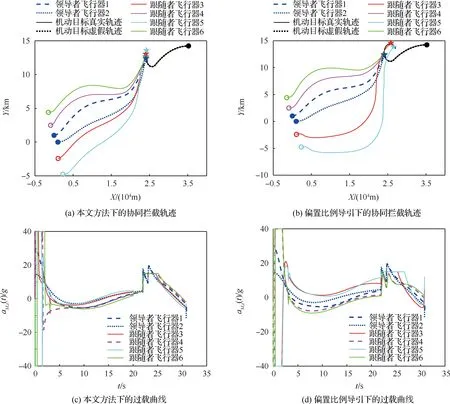
图19 协同围捕制导效果与偏置比例导引制导效果对比Fig.19 Comparisons between cooperative encirclement hunting guidance and proportional guidance
两种方法的脱靶量如表4所示。可以看出本文提出的方法下,目标逃逸概率为0%,偏置比例导引方法下的目标逃逸概率为50%。
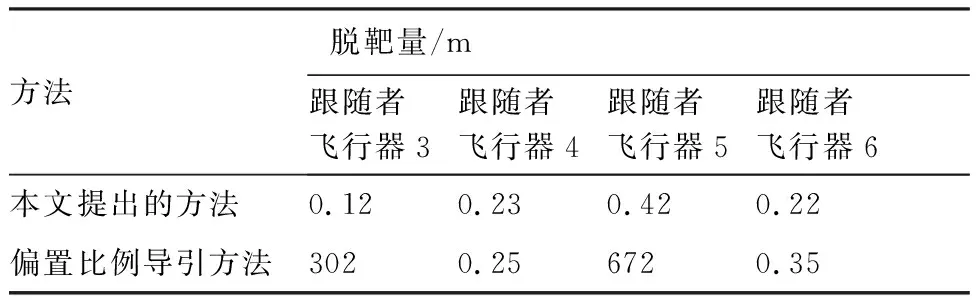
表4 不同制导方法的脱靶量Table 4 Miss distance of different guidance laws
两种方法的平均过载积分如表5所示。可以看出本文提出的方法下,平均过载积分为209.4 m/s,偏置比例导引方法下平均过载积分为251.9 m/s。偏置比例导引方法下过载大的原因是该方法不能进行弹道形状的控制。

表5 不同制导方法的平均过载积分Table 5 Average overload integral of different guidance laws
为了分析初始进入误差,1(0)对飞行器过载变化影响,以飞行器3为例进行仿真,结果如表6 所示。可以看出初始进入误差越大,拦截所需的平均过载越大。

表6 跟随者飞行器3不同初始进入条件下的平均过载积分
基于图19,根据假设4后的描述,在攻角并不是太大的时候,由于导引头的瞬时视场角一般是个小量,可近似前置角,()代替[35]。根据前置角曲线可以看出,本文方法的探测视场角比偏置比例导引方法下探测视场角小,因此探测效果更好。原因是本文的方法能进行弹道形状的控制,目标是使得制导误差尽可能小。
5 结 论
1) 研究了针对机动目标的多飞行器协同围捕拦截问题,基于狼群协同围捕猎物中的行为学机理,提出了一套多领导者-多跟随者模式下的分布式协同围捕制导方法。
2) 针对多领导者飞行器,设计带有目标机动补偿的协同逆轨拦截制导律,能够为跟随者飞行器提供一个良好的末端拦截阵位以及围捕拦截的参考轨迹。
3) 针对多跟随者,构建了分布式状态器实现对领导者的状态轨迹凸组合估计。设计了带有抗过载饱和机制的时变围捕视线角编队跟踪制导律,实现了对机动目标的多方向围捕拦截。
4) 设计3组不同场景下的仿真示例,对分布式协同围捕制导方法的有效性进行了验证。

