平稳随机载荷的信号特征提取与深度神经网络识别
杨特,杨智春,*,梁舒雅,康在飞,贾有,2
1. 西北工业大学 航空学院,西安 710072 2. 太原科技大学 应用科学学院,太原 030024
工程结构受到平稳随机载荷作用时,常常因动载荷频带范围覆盖结构的固有频率引起结构共振,从而引发结构振动破坏和疲劳失效等。因此准确识别结构所受的动载荷,掌握结构所处的动载荷环境,对于工程结构的动强度设计、校核与结构健康检测等工作,具有重要的作用。
传统的动载荷识别方法往往直接从频域振动方程出发,用系统矩阵求逆解算出动载荷列阵,但这些方法需要结构精确的动力学模型,而对于复杂的工程结构,其精确结构动力学模型的建立往往并不容易,导致传统动载荷识别方法在实际应用中的局限性。随着数据科学与智能算法的发展,以卡尔曼滤波和神经网络为代表的智能算法被学者引入动载荷识别领域,发展出基于数据统计与估计的动载荷识别新方法。
基于卡尔曼滤波算法,一些学者根据递归最小二乘法公式中权系数的选取方式,提出了常系数、自适应权系数和智能模糊权系数3种 类型的动载荷识别方法。Lee和Chen分别采用这3种权系数来识别动载荷,结果表明,智能模糊权系数收敛性好,且能够有效降低各种误差对识别结果的不良影响。对于大多数参数完全已知的线性动力学系统,采用直接的卡尔曼滤波算法便可实现结构的动载荷识别;然而,当受载结构存在部分动力学参数未知,或存在一定的非线性动力学因素时,则需要用到扩展的卡尔曼滤波方法,并与其他的估计算法相结合进行动载荷识别应用。
扩展卡尔曼滤波方法的思路是对非线性动力学系统进行泰勒级数展开,并忽略高阶项,保留低阶项,从而将非线性动力学系统实现线性化;之后再进行进一步的处理与动载荷识别。Ma、Lourens、Yang等对方法进行了较为详细深入的探究,证明了方法具有良好的适用性。然而,这一类方法仍然存在一定无法避免的局限性与缺陷:一方面,基于统计与状态估计的动载荷识别方法一方面仍然是需要基于一定精度的动力学系统模型;另一方面,递归计算的特性也导致计算容易出现累积误差和计算结果的收敛性容易受动响应测试噪声影响。
张方和朱德懋利用前馈神经网络模型进行了动载荷识别的尝试,仿真和实验结果表明,该方法具有可行性。但限于当时计算机发展的条件限制,该方法未能进一步深入研究。近年来,随着计算机技术的飞速发展,人工智能(Artificial Intelligence)已经成为一个具有众多实际应用和活跃研究课题的领域,而以深度学习为依托的深度神经网络则成为人工智能领域目前最为重要的组成部分,并在各个领域均得到成功的普及与应用,深度学习也为处理海量数据以及在科学领域做出有效的预测提供了强有力的工具,例如在预测分子相互作用、搜索亚原子粒子等各个领域,深度学习技术均得到了成功的应用。同样,在动载荷识别领域,基于深度学习的动载荷识别方法也得到发展。Chen等利用深度神经网络(DNN)实现了刚体对半球壳体结构的冲击载荷识别。Zhou 等提出了一种利用深度循环神经网络(DRNN)对非线性结构的冲击载荷识别的新方法,通过对阻尼杜芬振荡器、非线性三自由度系统以及非线性复合板3种非线性结构的冲击载荷识别验证,结果表明,提出的方法能够实现仿真和实验系统所受到的冲击载荷。
然而,针对工程结构常常遇到的平稳随机载荷,基于深度学习技术识别的研究则开展不多。夏鹏等依据有限长脉冲响应(Finite Impulse Response)的原理,结合时延神经网络的“记忆”特点,提出了基于时延神经网络的针对平稳随机载荷的倒序识别法。实验结果表明,该方法可以准确识别出作用于铝制悬臂板上的2点的平稳随机载荷。但时延神经网络的“记忆”特性源于其网络内部结构的“时延”模块,随着时延步数的增加,其神经网络的内部参数也会出现指数级的增加,使神经网络模型的训练难度会随着网络规模的扩大而急剧增加,也导致训练过程容易出现局部收敛的状况。
同时,采用深度神经网络模型进行动载荷识别,其关键是利用深度神经网络模型挖掘数据特征,由此拟合数据之间的相关关系;由此,本文基于结构动力学系统的线性叠加原理,首先采用小波变换对“动载荷—动响应”的训练样本进行信号特征提取,利用这些特征信息训练出具有“选择记忆”特性的深度神经网络——长短期记忆网络(Long-Short Term Memory, LSTM),随后用平稳随机动响应样本的特征信号,识别出对应的平稳随机载荷样本的特征信号,再重构出平稳随机载荷时间历程样本。
基于神经网络的动载荷识别方法,其关键是基于数据特征之间对应关系的拟合,而平稳随机信号的特征主要在频域中体现,如信号的功率谱密度等。因此,要在时域内获得平稳随机信号样本的数据特征,需要对平稳随机信号进行信号特征提取,可利用小波变换将其分解为多层次的特征信号样本。对于线性结构,依据“动载荷—动响应”关系的线性叠加原理,经分解后各层次的动载荷信号特征信号样本与其对应层次的动响应信号特征样本之间存在确定的物理关系。采用LSTM神经网络搭建特征信号样本之间的相关关系,从而实现利用平稳随机响应样本的各层次特征信号,识别平稳随机载荷样本的各层次特征信号,最后,利用所识别动载荷样本的特征信号重构出待识别时域平稳随机载荷的样本。
1 LSTM神经网络
LSTM神经网络模型属于传统的循环神经网络模型(Recurrent Neural Network, RNN)的变种,基于如图1(a)中RNN模型的基本结构,在RNN模型中每一个神经元中引入门结构,如图1(b) 所示。如图1(a),为RNN中神经元的第步输入,指代神经元内部运算机制,为神经元第步运算的内部状态量,为神经元的第步的输出;表示时刻。传统的RNN模型通过其网络结构可以对输入数据“循环保留”,由此使其在针对序列问题的处理上,相比于其他神经网络能够更具优势。然而当输入数据为长序列数据时,RNN对数据的过度保留导致在神经网络的训练过程中,RNN容易出现梯度消失和梯度爆炸等问题,使其针对长序列数据问题难以处理。而LSTM神经网络由于门结构的添加,使其具有“选择记忆”的特性,从而在保留循环神经网络对序列数据处理的优势之外,LSTM神经网络能够具有足够的能力处理长序列数据问题。
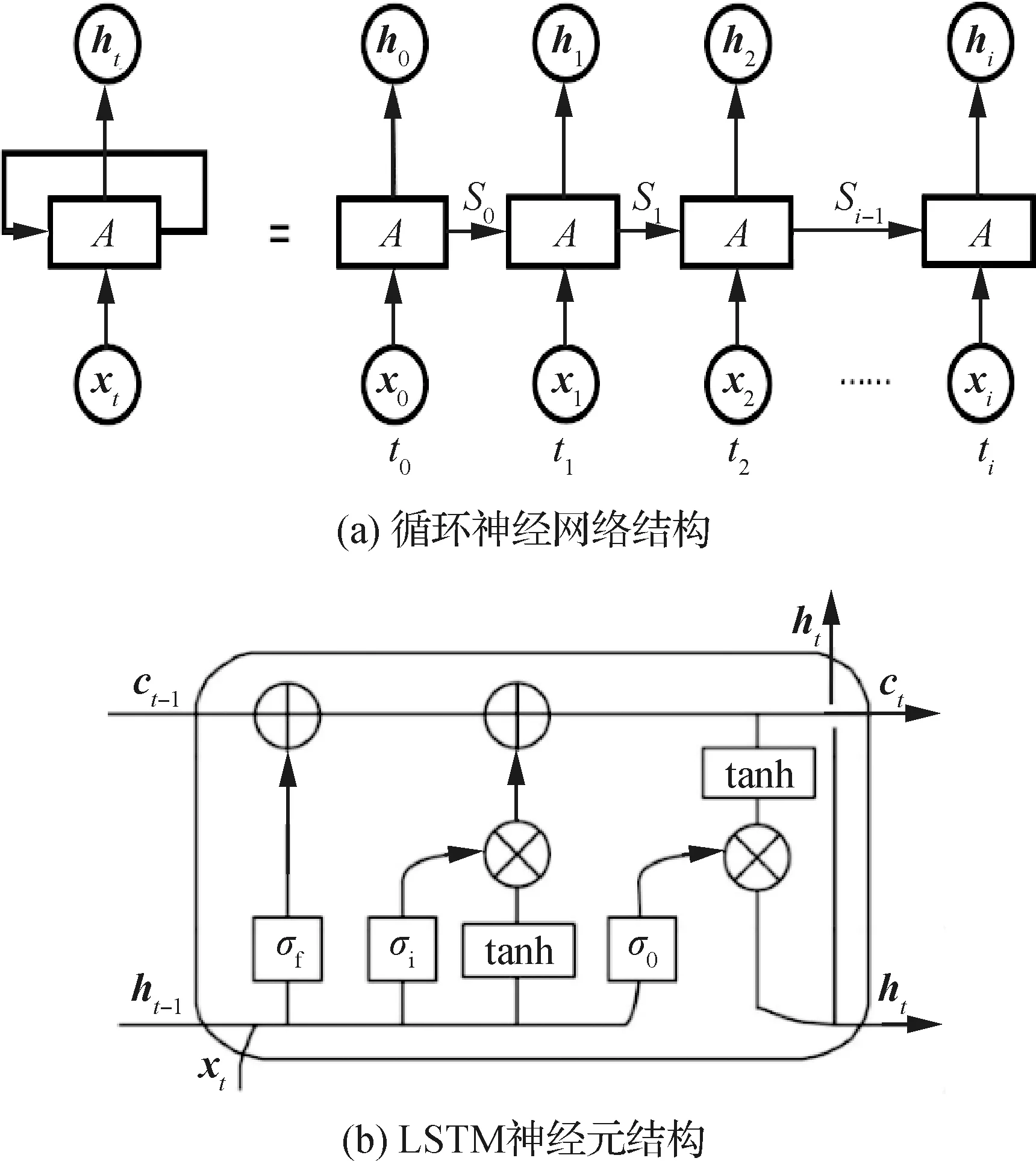
图1 LSTM神经网络Fig.1 LSTM neural network
在LSTM神经网络中,常规的神经元被储存单元代替,每个储存单元由输入门、输出门和遗忘门组成,LSTM使用门控机制更好地构建数据中的长期依赖关系,来实现时间上的记忆功能,防止梯度消失的发生。图1(b)中的表示sigmod激活函数。遗忘门、输入门、输入节点、输出门、本单元状态及本单元输出的计算表达式为
=(+-1+)
(1)
=(+-1+)
(2)
=(+-1+)
(3)
=(+-1+)
(4)
=⊙+-1⊙
(5)
=()⊙
(6)
式中:为时刻单元的输入;-1为上一时刻隐含层的输出向量;、、、、、、、为权重矩阵;、、、是对应的偏置向量; ⊙表示向量中元素按位相乘;表示tanh函数;则是存储了时刻及之前时刻所有有用信息的隐含状态向量。
由于LSTM神经网络的主体结构的输入不仅来自于输入层,还有一部分来自于上一时刻循环的状态,且通过遗忘门的选择性遗忘,使其具有“选择记忆”的特性。
2 用小波变换提取特征信号
小波变换作为一种良好的时频分析工具,能够将数据划分为不同的频率分量,然后用一种与其尺度相适应的分解来每一分量,由此可以实现同时在时域和频域内聚焦信号的演变,对于结构“随机动载荷—动响应”信号,利用小波变换对其进行信号特征提取具有独特的优势。
2.1 小波基函数选取
结构的频响函数通常是基于系统传递函数的傅里叶变换而定义,因此本文选取具有紧支撑傅里叶变换特性的Meyer小波作为小波基函数。Meyer小波由Yves Meyer在1985年提出,是首个具有光滑性的正交小波基,其同时兼具了对称性、紧支撑性等优点。正交性使分解后的各尺度信号间没有冗余的信息,对称性保证分解后信号中小波相位的线性,时域的紧支撑保证了信号时间特性的保留,而频域的紧支撑使得信号分解的频域划分得更为严格,因而在对宽频随机信号进行分解时,Meyer小波可以清晰地划分出各频带,且各频带信号之间不会互相影响产生混叠。
Meyer小波的基函数是在频域内定义的,即


(7)
式中:表示小波基函数;为小波基函数的相位;()为辅助函数:
()=(35-84+70-20)∈(0,1)
(8)
2.2 信号样本的特征信息提取
利用小波变换对平稳随机信号进行多频率分辨率分解可得:
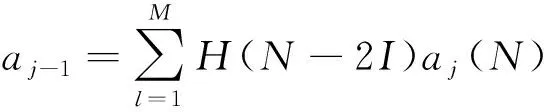
(9)
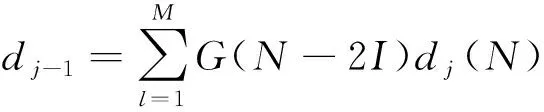
(10)
式中:为低通滤波器;为高通滤波器,不同的小波基对应不同的高、低通滤波器;()为信号的低频部分,也称为离散近似信号;()为信号的高频部分,也称为离散细节信号;为滤波器组中滤波器系数的个数;为小波分解的尺度,=2;为分解层数;为滤波器阶数。
3 动载荷信号特征深度神经网络识别
3.1 “动载荷-动响应”特征信号关系
线性结构作为线性时不变系统,作用于其上的动载荷与结构的输出动响应存在确定性关系,同时输入与输出关系上满足线性叠加原理。以线性单自由度振动系统为例,当系统受到一段平稳随机载荷()作用时,基于式(7),可利用小波变换将动载荷信号样本()利用阶的Meyer小波将其分解为个不同频段下的定频变幅值的动载荷特征信号样本()、()、…、()的叠加,其中任意一个层次的动载荷特征信号样本()可被描述为
()=()sin
(11)
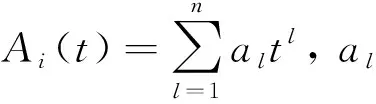


(12)

(13)
式中:、、分别为单自由度振动系统的质量、阻尼和刚度。由于等式(12)为二阶常系数非齐次线性微分方程,因此系统的稳态位移响应(),既方程的特解一定具有如下形式:

(14)
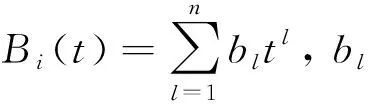
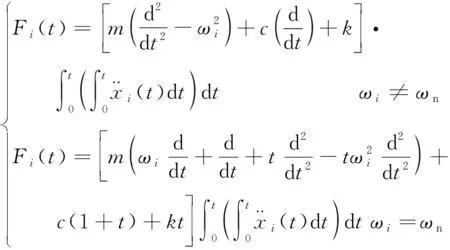
(15)
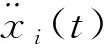
3.2 平稳随机载荷样本的特征信号识别
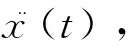
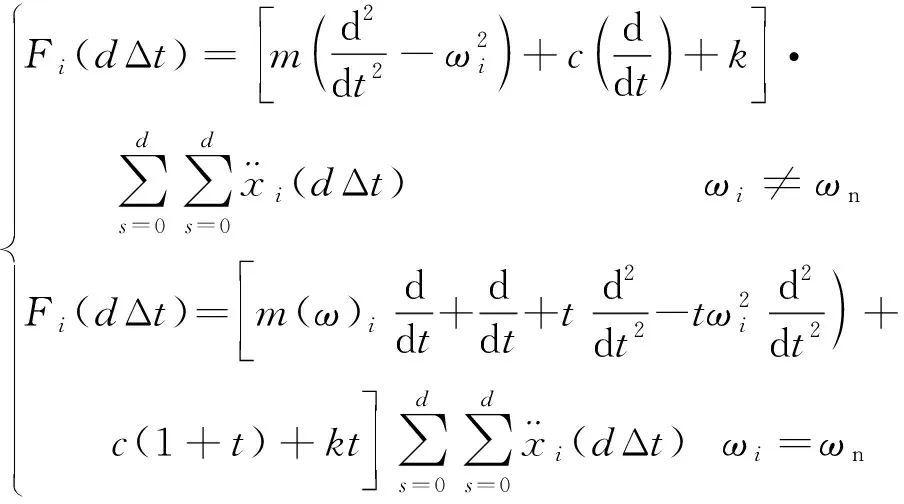
(16)
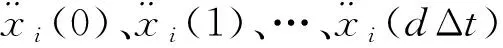
4 动载荷时频特征识别的仿真验证
建立三自由度振动系统如图2所示,其中系统各自由度集中质量=2 kg,弹簧刚度=4 000 kN/m,系统黏性阻尼=60 kN/m·s。系统的3阶固有频率分别为3.167 6 Hz,8.875 5 Hz及12.825 5 Hz。
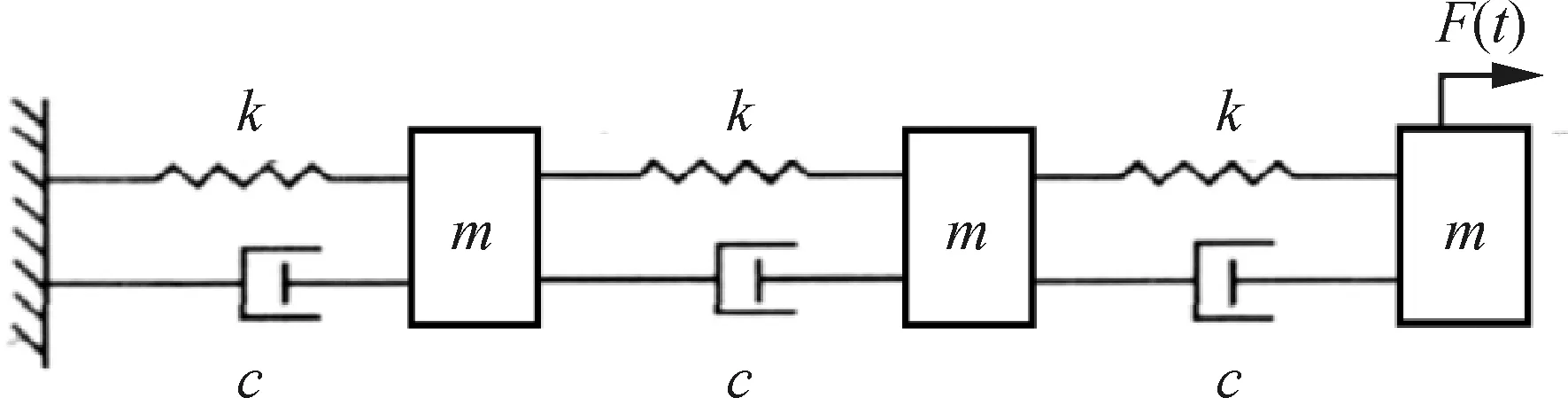
图2 三自由度振动系统Fig.2 Three-degree-of-freedom vibration system
三自由度振动系统的如下:
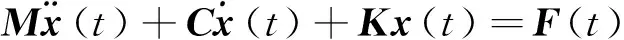
(17)
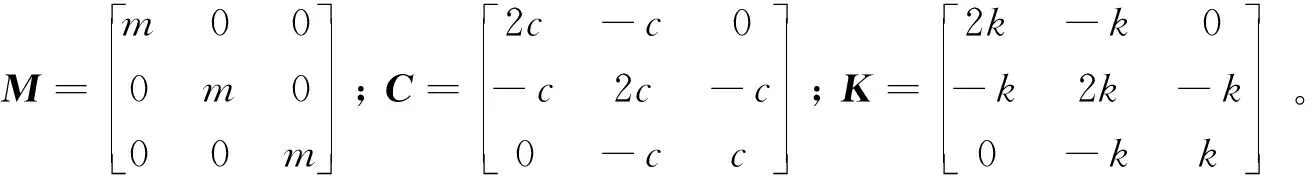
对三自由度振动系统动载荷识别所构建的LSTM神经网络模型的结构共有7层,如图3所示,其中2层LSTM层神经元个数均为128,RELU层为线性整流激活函数层。
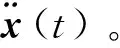

图3 LSTM神经网络模型Fig.3 Model of LSTM neural network
将3自由度振动系统各频率下动载荷特征信号样本的识别结果叠加后获得的识别动载荷样本与真实载荷样本对比如图4所示,两者的时间历程曲线吻合度较好;同时定义识别动载荷样本时间历程曲线与真实动载荷样本时间历程曲线的均方根值相对误差RMSE与相关度如下:
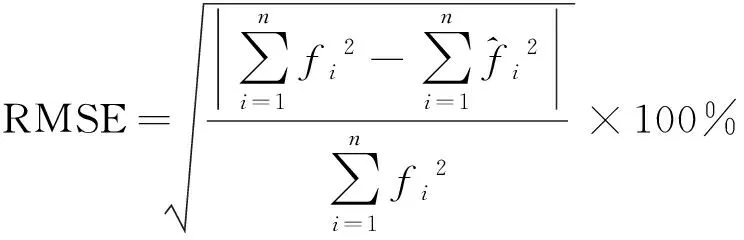
(18)
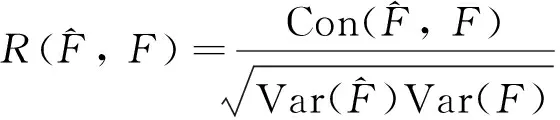
(19)
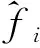
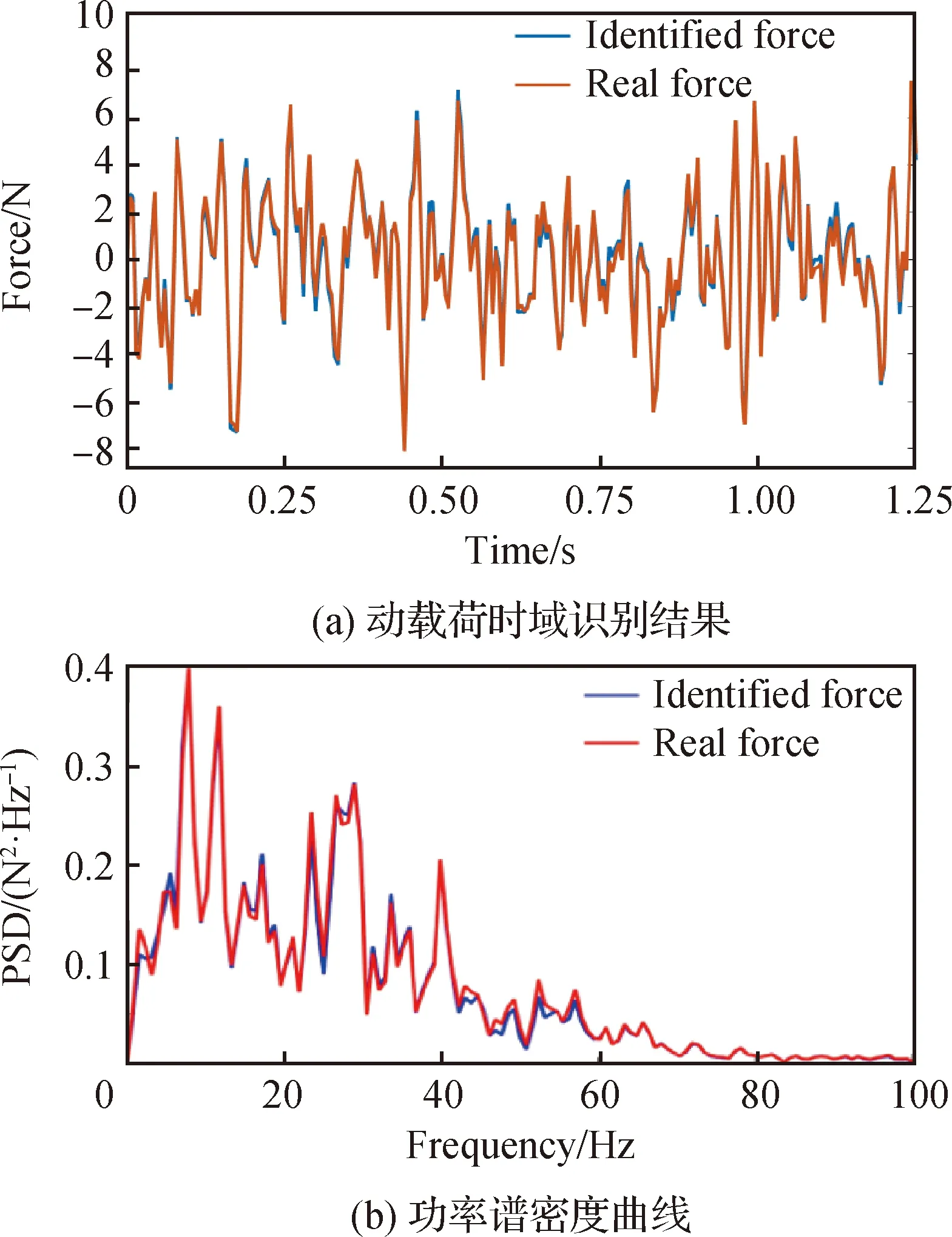
图4 三自由度振动系统动载荷识别结果Fig.4 Identified dynamic load of three-degree-of-freedom vibration system
同时,定义识别动载荷样本功率谱密度曲线的置信度如下:
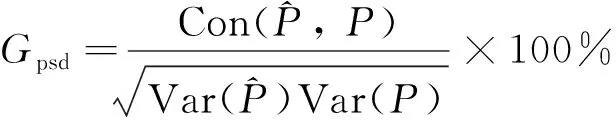
(20)

考虑到工程实际中不可避免地会遇到测量噪声的问题,因此对本文所提出方法的抗噪能力进行考察。分别对测试集动响应样本添加5%、10%和15%的白噪声,获得的动载荷识别结果如图5所示;经计算,存在5%测量噪声时,动载荷样本识别结果与真实载荷样本的相关度为98.70%,均方差值相对误差为3.37%,PSD置信度为98.99%;存在10%测量噪声时,动载荷样本识别结果与真实载荷样本的相关度为96.54%,均方差值相对误差为7.16%,PSD置信度为97.30%;存在15%测量噪声时,动载荷样本识别结果与真实载荷样本的相关度为93.76%,均方差值相对误差为15.27%,PSD置信度为92.24%。可见本方法具有良好的抗噪能力。

图5 噪声影响下的三自由度振动系统动载荷识别结果Fig.5 Identified dynamic load of three-degree-of-freedom vibration system with measuring noise
5 动载荷信号特征识别的实验验证
为了用实验方法来验证平稳动载荷深度神经网络识别方法的工程实用性,采用一个加筋壁板模型来进行动载荷识别实验,如图6(a)所示。加筋壁板实验模型由铝板和铝制框架组成,框架结构四边采用U型铝材,中间为工字形铝材,所采用的铝材厚度为4 mm;框架外轮廓尺寸为880 mm×380 mm×60 mm,内轮廓尺寸为800 mm×300 mm×60 mm,中间工字梁铝材尺寸为300 mm×80 mm×60 mm;铝板尺寸为880 mm×380 mm×4 mm。铝板模型采用左右两边固支的支撑条件安装于基础支架。采用实验模态测试方法得到加筋壁板结构模型的前6阶固有频率如表1所示。

图6 加筋壁板实验布置Fig.6 Experimental set-up of stiffened panel
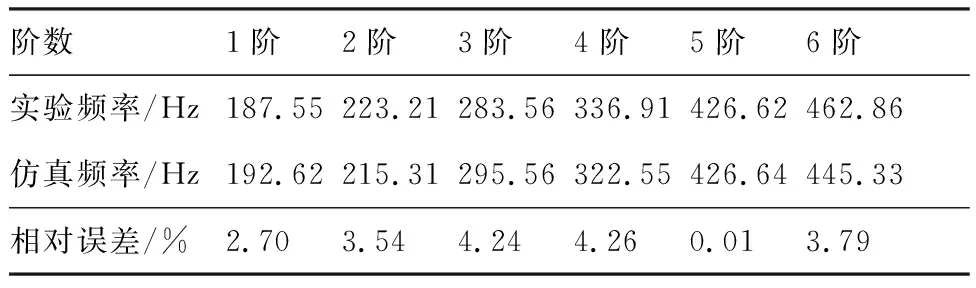
表1 加筋壁板模型的固有频率Table 1 Natural frequency of stiffened panel model
如图6(b)所示,采用2个电磁激振器分别于#1点和#2点对加筋壁板模型施加垂直于壁板平面的平稳随机载荷,同时在图6壁板的A1~A10位置分别布置加速度传感器,测试结构的加速度响应。
加筋壁板结构前6阶固有频率均在500 Hz以内,因此分别对#1与#2激励点,由2段不同的白噪声信号,分别各自经过一个带宽为5~500 Hz 的带通滤波器进行滤波,得到的一段频率范围在5~500 Hz平稳随机信号,用其一个样本作为平稳随机激励驱动激振器对加筋壁板进行加载,并采集加筋壁板模型的“动载荷—动响应”数据。采用8阶Meyer小波分别将动载荷时间历程和获取到的模型各测点的动载荷与加速度响应时间历程分解为8层的特征信号样本,截取各层次特征信号的平稳阶段,并将其分别划分为训练集、验证集与测试集。采用3.2节中结构与初始参数皆相同的LSTM神经网络进行训练与测试,识别动载荷样本与真实动载荷样本历程的对比如图7所示。样本信号的采样率为2 048 Hz,设置采样点数为4 096,频率分辨率为0.5 Hz,选用汉宁窗作为窗函数,计算求得动载荷样本的功率谱密度函数曲线(PSD)。采用式(18)、式(19)进行计算,动载荷识别时域识别结果中,#1点样本均方根相对误差为3.92%,识别动载荷样本与真实动载荷样本的历程曲线相关度为98.83%,PSD置信度为99.62%;#2点样本均方根相对误差为4.95%,识别动载荷样本与真实动载荷样本的历程曲线相关度为98.48%,PSD置信度为99.43%。识别动载荷样本与真实动载荷样本的功率谱密度函数曲线吻合很好。
为进一步考察本方法对于随机动载荷的识别能力,采用获得的深度神经网络模型进一步对与模型训练载荷具有不同谱型分布的宽带和窄带随机动载荷进行识别。对#1号与#2号激励点,由2段不同的白噪声,分别各自经过一个带宽为5~200 Hz的带通滤波器进行滤波后得到频率范围为5~200 Hz的平稳随机信号,以其一个样本作为平稳随机激励驱动激振器对加筋壁板进行加载,并采集加筋壁板模型的“动载荷—动响应”数据,作为宽带随机动载荷识别验证样本。之后,对#1号与#2号激励点,由2段不同的白噪声,分别各自经过一个带宽为90~100 Hz的带通滤波器进行滤波,得到的一段频率范围在90~100 Hz平稳随机信号作为平稳随机激励驱动激振器对加筋壁板进行加载,并采集结构的“动载荷—动响应”数据,作为窄带随机动载荷识别验证样本。
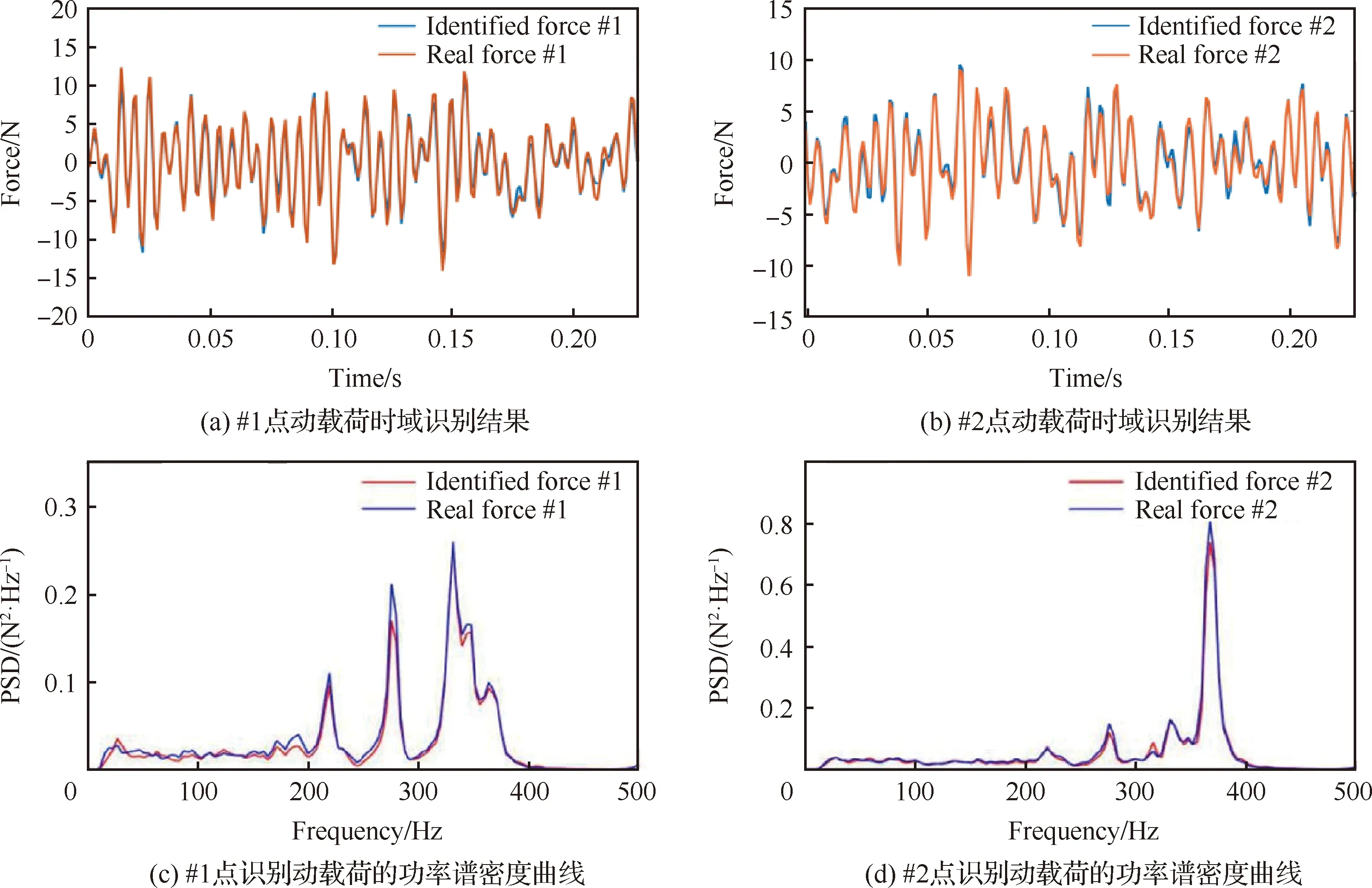
图7 加筋壁板结构动载荷识别结果Fig.7 Dynamic load identification result of stiffened panel
分别对频带范围为5~200 Hz的宽带随机动载荷和频带范围为90~100 Hz的窄带随机动载荷进行识别,识别结果如图8所示。样本信号的采样率为2 048 Hz,设置采样点数为4 096,频率分辨率为0.5 Hz,选用汉宁窗作为窗函数,计算求得动载荷样本的功率谱密度曲线(PSD)。经计算所得,对于宽带随机动载荷进行识别,#1点样本均方根相对误差为2.72%,识别动载荷样本与真实动载荷样本的历程曲线相关度为96.78%,PSD置信度为99.62%;#2点样本均方根相对误差为8.76%,识别动载荷样本与真实动载荷样本的历程曲线相关度为96.88%,PSD置信度为99.43%。对于窄带随机动载荷进行识别,#1点样本均方根相对误差为2.73%,识别动载荷样本与真实动载荷样本的历程曲线相关度为98.75%,PSD置信度为99.75%;#2点样本均方根相对误差为2.13%,识别动载荷样本与真实动载荷样本的历程曲线相关度为98.59%,PSD置信度为99.63%。由此可见,本方法对作用于线性时不变结构的随机动载荷具有良好的识别能力。
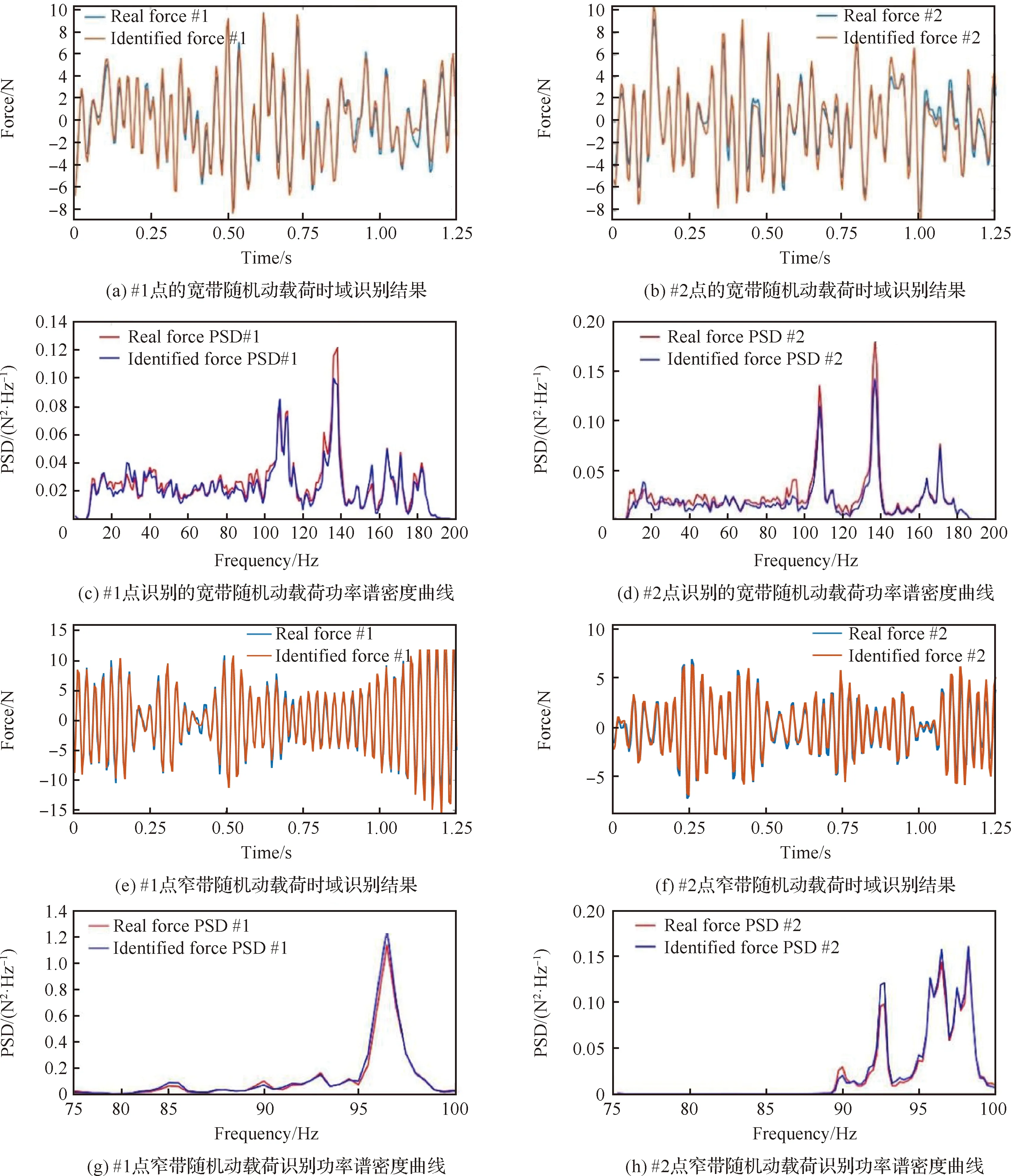
图8 其他谱型随机动载荷识别结果Fig.8 Random dynamic load identification results
6 结 论
本文将LSTM神经网络应用于动载荷识别领域,针对平稳随机载荷识别问题,从线性时不变结构的动力学特性出发,结合LSTM神经网络模型的“选择记忆”特性,利用小波变换的信号特征提取特性,提出一种采用信号特征的平稳随机载荷神经网络识别方法。通过离散系统的动载荷识别仿真以及壁板结构的动载荷识别实验结果,得到如下结论:
1) 相较于传统动载荷识别方法,本方法可以利用先进的人工智能技术建立基于数据驱动的代理模型,从而避免了建立待识别结构精确数学模型的困难。
2) 针对平稳随机载荷识别问题,本方法提出了从时域角度的识别办法,相较于频域识别方法,时域识别结果更加直观,也能够提供更多动载荷的有效信息。
3) 相较于现有基于神经网络的动载荷识别方法,经理论推导证明,本方法具有更加充足的原理支撑性,且基于特征信号样本的动载荷识别降低了神经网络模型拟合关系的复杂程度,进一步保证了神经网络的泛化能力。

