基于翼尖链翼的组合固定翼无人机研究

周伟,马培洋,2,*,郭正,王道平,周睿孙

1. 火箭军工程大学 导弹工程学院,西安 710025 2. 中国人民解放军66011部队,北京 102600 3. 国防科技大学 空天科学学院,长沙 410073 4. 火箭军工程大学 基础部,西安 710025

无人机(Unmanned Aerial Vehicle, UAV)是战争催生的产物,它诞生于一战,发展于二战。随着需求的多样化发展,无人机技术逐步进步,分支也越来越多,不只在军事侦察、物资运输、通信中继等国防工程上发挥重要作用,还广泛地应用于农业植保、环境保护、管线巡查等诸多民生领域。无人机按平台构型主要分为固定翼无人机、旋翼无人机、扑翼无人机等。固定翼无人机相比于其他无人机具有速度快、载重大、航程长等优势。

无人机集群,能够完成大量单机系统无法完成,或者由群体更有效完成的任务。但是固定翼无人机组成的集群相比于高空长航时无人机存在航时短、巡航高度低的不足。通常,为了保证集群无人机良好的机动性能,其采用的无人飞行单元一般体积较小、展弦比不大,加装太阳能能源模块收效甚微。为同时获得高空长航时无人机和无人机集群的双重优势,笔者所在团队提出了链翼的概念,类似理念的研究和试验在近现代航空发展上已有探索。

本文梳理了与链翼无人机相关的技术发展历程与工程研究现状,从理论上分析了其在升阻比、飞行速度、续航时间核巡航高度上的优势阐述了以空中对接为首的关键技术,并对未来发展进行了展望。

1 链翼的概念

链翼技术(Chained Wing Technology, CWT),是指多架固定翼无人机通过翼尖连接机构将机翼连接,形成一个大展弦比无人飞行器组合体的大气层内空中连接与分离技术。其中,被连接的单个固定翼无人机也称为无人飞行单元。

基于翼尖链翼的组合固定翼无人飞行器(Combined Fixed-Wing Unmanned Aerial Vehicle with Wingtip Chained, CFWUAV-WC)利用翼尖链翼技术使飞行器具有更好的空气动力学性能、结构强度与复杂多任务适应性能,可以飞得更高,续航时间更长,遂行任务更加灵活多样,同时也可在一定程度上避免常规高空平台系统(High Altitude Platform Systems, HAPS)机翼负载过大的问题。

组合固定翼无人飞行器的不同飞行单元可以根据任务需求搭载不同载荷,通过这些相同或不同的载荷共同执行复杂多任务。在飞行过程中,各飞行单元可以自由组合和分离。分离时,可以确保灵活机动;组合时,具有续航时间更长、飞行高度更高的优势。未来组成组合平台的无人飞行单元可以融合太阳能技术,实现昼夜不间断飞行,极大地提升组合无人飞行器综合任务执行的持续性,降低维护成本,无论是民用综合保障还是区域军事支援都能够发挥重要作用。

2 翼尖链翼技术进展

翼尖链翼技术最早可以追溯到二战后美国进行的翼尖耦合与拖拽试验,由于当时无法突破技术瓶颈和空中加油技术的冲击,该项研究停滞了40多年,直到21世纪,德国、美国和中国又有团队开始了相关研究。

2.1 国外早期的翼尖耦合与拖拽技术尝试

翼尖耦合(Wingtip Coupling,WC)的概念最早由二战后移居美国的德国科学家Richard Vogt提出,旨在通过在两翼翼尖附加两个存放燃油的飞行模块的方法增加战斗机航程,同时由于翼尖的飞行模块增大了展弦比,将有效降低诱导阻力,提高气动性能。基于这种概念,1949年美国空军改装了道格拉斯C-47运输机和小型Q-14靶机并进行了空中对接试验,用来验证翼尖拖拽飞行试验的可行性,如图1所示。

图1 C-47运输机翼尖拖拽Q-14靶机Fig.1 C-47 transporter wingtip dragging Q-14 target

试验成功后共和国航空公司(Republic Aviation)承接了“MX-1018”(即“Tip-Tow”)项目,目的是提高战斗机航程来为轰炸机护航,试验通过一架B-29轰炸机拖拽两架F-84喷气式飞机,实现了空中3机连接和飞行,并进行了电、氧、油的初步传输尝试,如图2所示。1953年4月24日的试验中由于自动控制问题导致2架飞机坠毁,6名机组人员全部遇难,该项目终止。

图2 “Tip-Tow”项目B-29拖带两架F-84飞行[6]Fig.2 Tip-Tow Project B-29 towing two F-84[6]

1955年,美军又开启了“Tom-Tom”项目,目的是远程输送侦察机对敌方领空进行侦察,使用的是比B-29翼展更大的B-36轰炸机,拖拽两架后掠翼布局的RF-84F照相侦察机,如图3所示。但在1956年9月23日的飞行试验中,两架飞机对接后RF-84F开始剧烈拍动,在飞行员主动抛除连接机构后,两机成功分离,没有造成严重后果,但“Tom-Tom”项目也自此停止。以上一系列试验验证了这种组合飞行技术在气动效率方面的优越特性,但也发现了克服两翼对接时的翼尖涡流是该研究的技术难点。

图3 “Tom Tom”项目B-36与RF-84F相互接近[7-8]Fig.3 Tom Tom Project: B-36 and RF-84F closing to each other[7-8]

翼尖拖拽技术受制于当时技术条件,造成了极大的安全隐患甚至人员伤亡,同时从提高航程的目的来看,空中加油技术的成熟也对翼尖耦合与拖拽技术产生了巨大冲击,加速了这一技术的没落。尽管如此,该技术在提升气动性能、增加航程方面的效果不可忽视。

2.2 国外近年来重启的翼尖连接技术探索

21世纪以来,随着无人机集群、太阳能技术的迅猛发展和飞行控制技术、传感器与测量技术的进步,能够完美融合集群无人机与太阳能无人机优势的翼尖耦合技术再次被科学家们关注。

德国科学家主要从工程上对翼尖连接技术进行了探索和实践,并着重设计了组合体的控制系统。柏林技术大学及其附属的AlphaLink项目股份有限公司(AlphaLink Engineering GmbH)开发了一个控制系统来控制通过翼尖连接的无人机组合体,并制造了由3架无人机通过翼尖相连的方式组合而成的技术验证机 (Advanced Multi-Body Aircraft),该验证机在2017年6月于Strausberg机场进行了首飞试验,如图4所示。结果表明,该控制系统可以保持多架链翼无人机的机翼形状。该公司现在正在进行基于太阳能动力的多无人机链翼项目——AlphaLink X,如图5所示,以AMBA控制系统为基础,利用大翼展和高升阻比以达到长航程目的,尤其结合太阳能动力后,希望实现全年滞空飞行。

图4 AMBA的飞行测试[9]Fig.4 Flight test of AMBA[9]

图5 AlphaLink X项目远景图[10]Fig.5 Vision of AlphaLink X project[10]

德国宇航研究院(Deutsches Zentrum für Luft-und Raumfahrt, DLR)为了解决大展弦比飞行器在飞行时出现大上反角情况导致结构被破坏的问题,于2017年提出了一种分布式大展弦比的高空弹性飞机(Elastic Aircraft for High Altitude, ELAHA)方案,如图6所示。该布局无人机由载荷段和推进段构成,载荷段采用刚性设计,而推进段采用大柔性设计,这种布局在局部上升气流作用下可以实现从翼梢到另一侧翼梢的90°弯曲,提高了结构安全性,同时利用柔性段平尾操纵实现全机飞行控制。此外,他们还希望该无人机可根据任务要求灵活进行各飞行单元的组合与分离,从而实现其他布局难以实现的任务目标。

图6 德国宇航研究院的高海拔弹性飞机概念[11]Fig.6 DLR concept of elastic aircraft for high altitude[11]

美国科学家主要通过计算流体力学分析与风洞试验,对翼尖连接过程的气动力与气动控制进行分析与研究。2002—2003年,Magill和Durham,进行了大量的风洞试验,对翼尖对接飞行、近距离编队飞行和拖拽编队飞行等3种复合飞行器运输(Compound Aircraft Transport, CAT)飞行模式进行了研究。结果表明,拖拽飞行最易实现,但需要载机配合。翼尖对接飞行和近距离编队飞行可以在无载机的条件下增强续航能力,但是翼尖对接飞行的空中对接过程是主要难题,同时对接后的飞行控制技术需进一步研究；而近距离编队飞行可以利用前侧飞行单元产生的气流,但其飞行状态变化剧烈,飞行单元之间的耦合影响较大,对飞行控制有更高的要求。

2012至今,Montalvo和Costello对如图7 所示的翼尖相连和首尾相连的飞行器进行了分析研究,提出了“元飞行器”(Meta Aircraft)的概念,并对元飞行器的飞行动力学与控制、连接动力学与控制,给出了仿真结果,后期还进行了如图8 所示的飞行试验,对控制算法进行了初步验证。

图7 组合无人机概念[14-16]Fig.7 Concept of combined UAV[14-16]

2018年,美国国家航空航天局的 Cooper和Rothhaar提出了多架飞机空中对接系统的动态模型和控制方案,动态模型由相邻两机翼的空气动力学模型(NASA-Burnham-Hallock wingtip vortex model)、固定翼飞机运动方程以及连接机构受力模型(Spring-damper-magnet System)组成。对接控制方案由一种将本飞行单元自主驱动到目标飞行单元的引导算法实现。

2.3 国内对翼尖连接与链翼技术的探索

2012—2013年,辽宁通用航空研究院的张立国等提出了两种联体飞机的想法,一种是平直布局,另一种是飞翼布局,并设计了一种连接机构。

2019年北京航空航天大学的An总结了团队对多体飞机(Multi-Body Aircraft, MBA)的飞行力学分析和试验情况,认为多体飞机能够解决与美国太阳神无人机事故类似的问题。并进行了双机连接在一起的验证飞行试验。

2021年中国科学院热物理研究所无人飞行器实验室的杨延平等综述了结构创新型的集群组合式柔性无人机(Flexible Modular Swarming UAV),从总体、气动、结构、能源、控制、通信等方面梳理和分析了此飞行器亟待解决的关键技术。

2021年南京理工大学的Wu等探究了翼尖连接对太阳能飞机降低能耗和增加飞机续航能力的影响,并导出了翼尖连接飞机的奥斯瓦尔德效率因子、诱导阻力系数和功率消耗模型。

2019年至今,笔者团队也进行了翼尖连接的探索和实践,并将多固定翼飞行器翼尖横向连接形成链式结构的技术称为链翼技术。通过如图9所示的连体飞机进行飞行试验,验证了双机链翼飞行比两架单机飞行在耗电相同的情况下具有更长的航时。该试验用一个整体制作的2倍长机翼代替2个紧密连接的机翼,以模拟具有足够连接强度且连接处密封良好的理想双机链翼状态,用两块相同工艺制作的常规机翼作为对照。试验使用雷迅V3飞控测试了单机和双机的平飞速度,统一了巡航海拔高度518 m(相对高度50 m),盘旋半径500 m,每次试验使用充满电的4块相同规格电池对链翼供电,为保证相似的天气状况,从链翼起飞开始,中间经过链翼降落、更换机翼、单机起飞,直到单机降落,试验时间控制在1 h以内。经多次飞行对照试验,结果表明链翼飞行相比单机飞行续航时间普遍提升11%～21%。

图9 续航对照试验采用的连体飞机Fig.9 Combined aircraft used in endurance control test

笔者该团队通过续航对照试验,验证了链翼的价值,进而开展了双机分离试验,如图10所示。图10(a)是试验所使用的可以实现空中分离的连接机构,该机构包括一个置于机翼内的继电器、一个电磁铁、一个粘贴了铁片的插销、一个带有固定槽的支架结构以及一个能与插销配合的扇形扁平销。如图10(b)所示,当飞行器执行空中分离操作时,通过控制继电器停止对电磁铁供电,使带有铁片的插销与电磁铁分开,进而差异控制两个飞行单元的航向,使扇形扁平销从原固定槽处滑出,从而实现双机空中分离。由于连接机构左右两侧质量不同,左翼翼尖处增加了配重。该试验开始是通过两个WFT07遥控器进行手动控制,通过教练线实现分离前副遥控器的统一指令控制,双机分离后,主遥控器关闭教练开关,主副遥控器可分别对两架飞机进行控制。后期逐步引入了能够对多无人机进行控制的多无人机规划调度系统,代替遥控器的部分功能,目前该系统在链翼控制模式中发挥作用不明显,主要用于分离后多无人机的程序控制。由于双机链翼飞行,飞行器进行滚转运动时,组合体如果简单按照多个飞行单元进行控制,靠近组合体对称轴的内侧副翼运动会削弱整体的滚转效果,因此增加了一个继电器控制内侧副翼电路通断,与控制连接机构的电磁铁继电器关联在了一个通道上,以降低模式切换时操作的复杂程度。

图10 双机链翼空中分离试验Fig.10 Air separation test of chained wing of double aircrafts

为了观察更一般的链翼飞行状态,笔者团队进行了如图11所示的3机链翼飞行试验,验证了 Montalvo提出的翼尖与翼尖相连飞行器的飞行控制效果：随着链翼数量的增加,滚转的响应逐渐减弱,但俯仰基本不受影响。同时还发现,由于没有加入对每个飞行单元独立的姿态控制,3架完全相同的飞行单元链翼飞行时,不论如何改变3架飞机的排列顺序,在空中均常常呈现中间突起、两侧下垂的飞行姿态,见图11(b),这是Behrens等提出的理论的一种表现,An等的分析和试验中也得到了这一结果。

3 链翼理论依据

翼尖链翼技术,其根本目的是将固定翼飞行单元通过翼尖连接机构,连接组合形成一个新型飞行器,以提高飞行器的气动效能。

基于二维翼型理论,三维有限长机翼的展弦比越大,升力分布越趋近于理想分布,实际升力越接近二维理论计算结果。同时,增大翼展有助于减小诱导阻力,从而提高升阻比。因此,通过合理的翼尖链翼,能够实现增加升阻比、减少能源消耗的目的。

下面重点围绕链翼无人飞行组合单元进行理论分析,梳理其在气动性能、续航能力、巡航高度和巡航速度上的优势,阐述链翼的理论依据。

3.1 链翼组合气动特性

为了更好的开展链翼气动特性的分析与对比,本节假设飞行单元链翼前后运动速度不变,姿态不变,飞行高度变化对大气密度的影响忽略不计。

3.1.1 升力特性

从升力线理论考虑,二维无限长机翼升力的理想分布如图12(a)所示。图中：为翼展,为升力。由于三维机翼并不是无限长,升力由机翼中部向翼尖逐渐退化,升力沿展向成椭圆分布,如图12(b)所示。总升力是升力曲线下的面积积分,从两图对比可以清楚的看到三维机翼相比二维理想情况有较大的损失。因此,展弦比越大,三维机翼的计算结果越接近二维理想机翼,单位展长产生的平均升力也就越大。

图12 2种机翼升力分布[12]Fig.12 Lift distribution of two kinds of wings[12]

如图13所示,为机翼展向坐标,为升力系数。从两架飞机连接前后的状态看,两个空白区为两架飞机未靠近时半个机翼的升力2×0.5,整个矩形区为连接后的总升力2×0.5,阴影区为两架飞机翼尖连接后增加的升力2Δ,这里

=+2Δ

(1)

式中：为单个机翼按照二维无限长模型计算的理想升力;为单个机翼按照三维有限长模型计算的实际升力;Δ为单个机翼单侧的升力差。所以,在外部条件不变的情况下,个单元连接形成链翼组合的升力,可以近似表示为

≈-2Δ

(2)

图13 2个飞行单元链翼前后的升力变化Fig.13 Lift variation of two flight units before and after wings chained

如图14所示,这里使用“近似”是由于链翼组合的升力系数沿展向分布并不能看作是矩形加两段椭圆弧(蓝色实线),而是与之非常相近的一整段椭圆弧(红色实线)。

图14 2个飞行单元链翼前后升力系数沿展向分布变化Fig.14 Lift coefficient changes of two flight units along spanwise distribution before and after wings chained

升力公式为

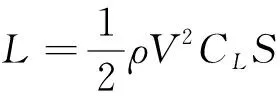
(3)

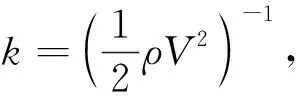
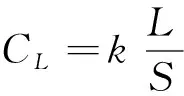
(4)

个链翼组合的升力系数可以表示为

(5)

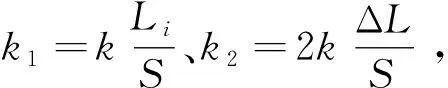
(6)

各点满足的拟合曲线如图15所示。由于是关于单调递增的,且无限趋于，所以,链翼后升力系数大于单个飞行单元的升力系数,且总存在<(+1),∈。

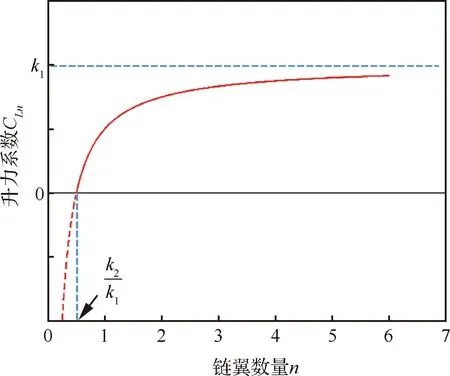
图15 CLn与n符合的拟合曲线Fig.15 Fitting curve of CLn and n

3.1.2 阻力特性

飞行器的阻力系数可以表示为

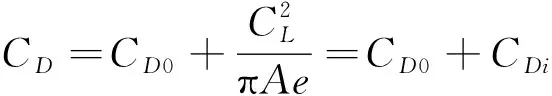
(7)

式中：为奥斯瓦尔德效率因子;为展弦比。最大升阻比情况下,寄生阻力系数0等于诱导阻力系数,且有

=20

(8)

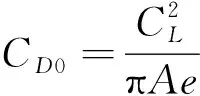
(9)

图16(a)和图16(b)分别表示链翼前后飞行单元机翼的状态,满足

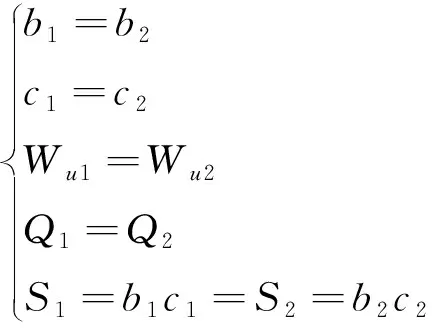
(10)

式中：1、2分别表示飞行单元1、2的重力；、表示飞行单元1、2的机翼展长；、表示飞行单元1、2的机翼弦长；、表示飞行单元1、2的动压；、分别表示飞行单元1、2的翼面积。

可进一步推导得到如下公式:

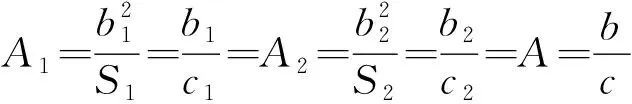
(11)

图16 链翼前后示意图Fig.16 Diagrams before and after wings chained

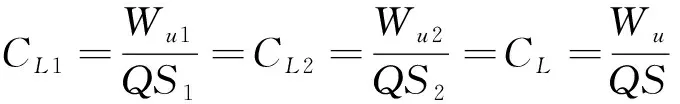
(12)

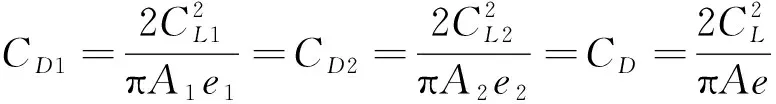
(13)

式中：、表示飞行单元1、2的展弦比；1、2表示飞行单元1、2的升力系数；1、2表示飞行单元1、2的阻力系数；==。

链翼后,由图16(b)可知,双机链翼组合平台的相关参数为=+,==,(1+2)=1+2,=,可进行如下推导:

=+=2

(14)

==2=2

(15)

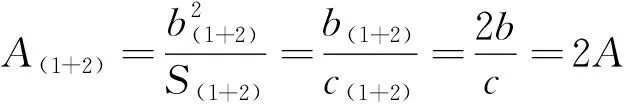
(16)

(1+2)=1+2=2

(17)

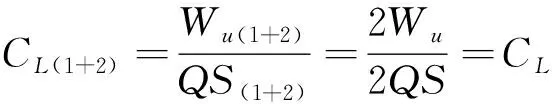
(18)

(19)

式中：下标(1+2)表示双机链翼组合平台。

同理,可以得到架链翼的阻力系数可以表示为

(20)

对于相同的飞行单元,为大于0的常数,奥斯瓦尔德效率因子,使用式(21)估算

=178(1-0045068)-064

(21)

式(21)为经验公式,通常∈(07,085)时有较准确的估算结果,对应的∈(663,1225),不在此范围时,估算结果偏差会增大,因此结果可能仅适用于两架链翼的情况。当个飞行单元组合后,链翼组合的展弦比=,奥斯瓦尔德效率因子可化为

=·068+114×(1-068)

(22)

递增时,阻力系数随链翼数量增加而减小,反之增大。令

()=-(-1)(-1)

(23)

化简得

()=(-114)[168-(-1)168]+114

(24)

在∈(07,085)的情况下,(2)>0恒成立,因此两架链翼的阻力系数小于单个飞行单元的阻力系数,即2<1。

如果继续增加链翼数量,由于奥斯瓦尔德效率因子估算式的适用范围有限,此方法不再适用。但考虑到翼尖连接能够消除内部翼尖处的诱导阻力,使平均阻力减小,类似于3.1.1节对升力系数的讨论,阻力系数有可能存在持续变小的趋势,且这个趋势逐渐减缓。

3.1.3 升阻比特性

若从最大升阻比的角度看,在本节假设前提下,寄生阻力系数0是不变的,由式(8)和式(9)可知:

(25)

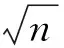
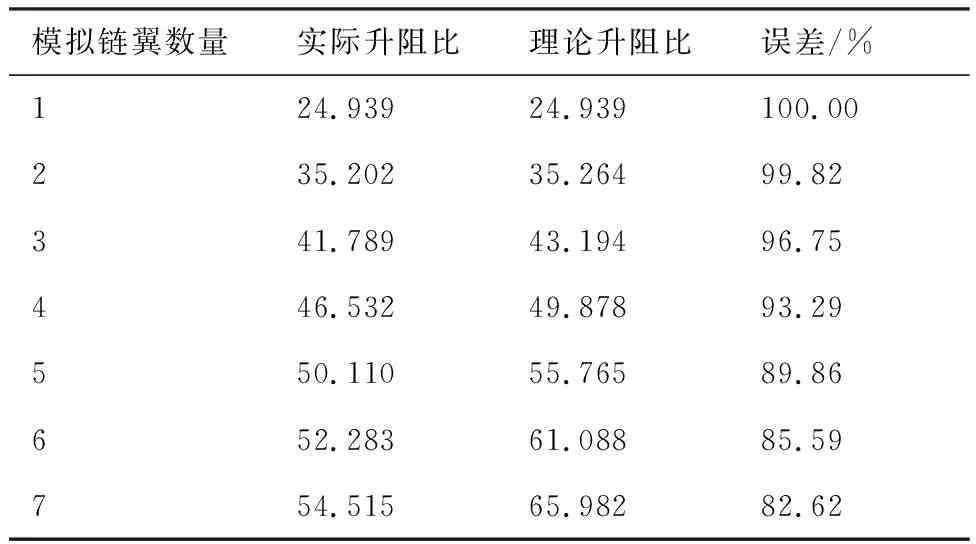
表1 链翼系统实际升阻比与理论升阻比的关系

根据表1数据绘制链翼系统实际升阻比与理论升阻比的关系见图17。考虑到飞行器的巡航状态升阻比一般接近最大升阻比,分析认为,飞行器的巡航状态升阻比在趋势上近似满足上述规律。

图17 链翼系统实际升阻比与理论升阻比的关系Fig.17 Relationship between actual lift drag ratio and theoretical lift drag ratio of chained wing system

3.2 链翼组合巡航速度

本节假设链翼前后飞行单元总满足受力平衡,保持水平直线飞行,飞行高度不变。对于能够始终保持机翼整体平直、翼尖处无缝隙的理想链翼模型,考虑水平匀速直线飞行时,应当满足方向上的受力平衡

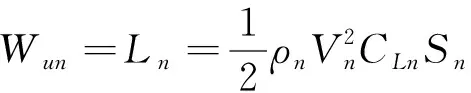
(26)

(27)

这里

=(+1)

(28)

由3.1.1节可知<(+1),∈,所以

>(+1)

(29)

因此,随链翼数量增加,链翼组合可以依靠更低的飞行速度进行巡航。

这里用改变展弦比的方法,模拟不同链翼数量时升力系数与巡航速度的变化,选用USA-35B翼型,弦长0.4 m,单机展弦比定为7.5,使用XFLR5软件的涡格法定升力计算,气动特性如表2 所示。

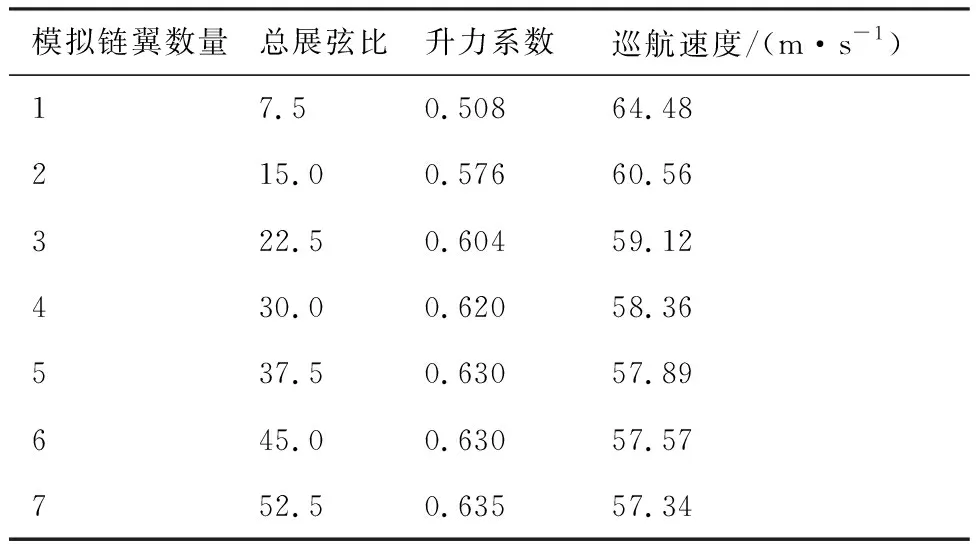
表2 总展弦比、升力系数、巡航速度随链翼数量的变化

根据表2数据绘制链翼系统升力系数、巡航速度随展弦比的变化见图18。可以看出,巡航速度需求随链翼数量增加而逐渐减小,从而降低了对动力、能源的消耗。

图18 链翼系统升力系数、巡航速度随展弦比的变化Fig.18 Variation of lift coefficient and cruise speed of chained wing system with aspect ratio

3.3 链翼组合续航能力

本节假设链翼前后飞行单元总满足受力平衡,保持水平直线飞行,飞行高度不变。对于单一飞行单元,在水平匀速直线飞行过程中,应当满足2个方向受力平衡

(30)

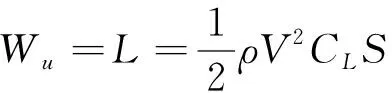
(31)

式中：、分别为无人飞行单元的发动机拉力和自身重力;、分别为飞行单元巡航飞行过程中的气动阻力和升力。

对于个飞行单元链翼的情况,巡航飞行仍然应当满足

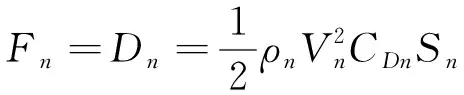
(32)

(33)

若考虑组合情况有

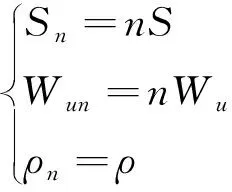
(34)

那么,式(31)除以式(33)得

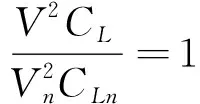
(35)

式(30)除以式(32)得

(36)

飞行单元单机和组合平台的升阻比可以分别表示为

(37)

假设链翼前后升力系数不变且飞行速度不变,将式(37)代入式(36)得

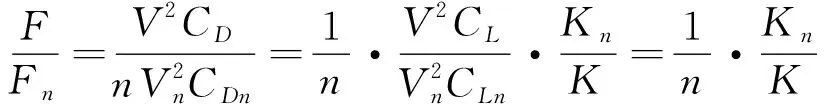
(38)

那么

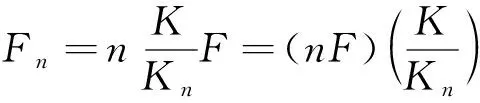
(39)

=()

(40)

式中:表示个飞行单元组合的拉力和；是升阻比之比,即单元升阻比与组合后平台升阻比之比,由3.1.3节可知组合后升阻比会增大,所以<1。

因此,个无人飞行单元组合后,其所需巡航拉力应当小于个飞行单元组合前所需巡航拉力的和,且组合后升阻比越大,巡航所需的拉力就越小,这样部分飞行单元的动力就可以关闭或交替工作,从而达到减少能源消耗,提高续航时间的目的。

若动力系统采用Cobra C-4120(430 kV)电机、1.5∶1减速组以及16×8的APC E螺旋桨,电源使用32 V机载电池。当组合体在2 km高度飞行时,其动力性能如图19所示。

图19 动力性能Fig.19 Dynamic performance

若机载电池容量为128 Ah,且采用各飞行单元动力系统输出功率相同的平衡动力策略,计算得到不同链翼数量时的工作电流与续航时间如表3 所示。根据表3绘制链翼数量与续航时间的关系如图20所示。可以看出,当飞行单元数量增大到7时,按照平衡动力策略,续航时间由256.6 min增大到了496.2 min,增幅接近93%。

表3 链翼数量对工作电流、续航时间的影响

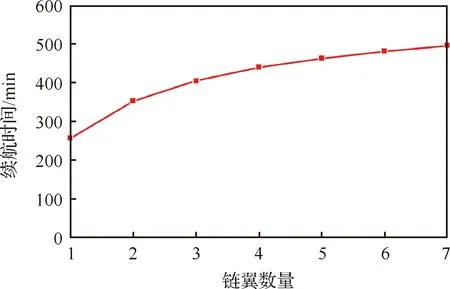
图20 链翼数量与续航时间的关系Fig.20 Relationship between number of flight units of chained wing system and endurance time

因此,增加飞行单元数量,能够有效提升续航时间。

3.4 链翼组合巡航高度

本节假设飞行单元链翼前后运动速度不变,姿态不变,密度随飞行高度变化而变化。

由3.2节可知,速度随链翼数量增加而逐渐减小。根据1976标准大气公式,由50 km内大气密度随高度变化结果绘制图21。可以看出,大气密度随高度升高而降低。根据式(33)的受力平衡,在飞行速度不变的情况下,链翼可以在密度更低时保持平飞,即链翼可以提升巡航高度。

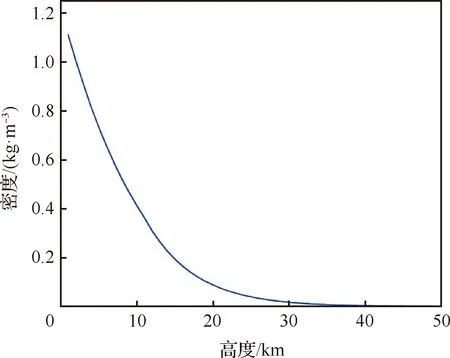
图21 50 km内大气密度随高度变化规律Fig.21 Variation of atmospheric density with altitude within 50 km

3.5 链翼组合飞行单元数量

在架链翼基础上,每一段相对于内侧的上反角,即连接机构处的两机翼夹角的补角,均有一个长度为(-1)的,最优化的向量来表示每个上反角的取值,在这个最优情况下,链翼整体在满足一定的稳定性条件的基础上,具备最优的升阻比；选择太阳能为动力时,在最优的航向前提下,具备最优的能量收支效果。

对于常规布局的固定翼飞机而言,由于载荷主要分布在机翼中央的机身内,随着展弦比的增加,由于机翼刚度有限,机翼投影面积与机翼面积的比值逐渐减小,增加翼展不一定会取得良好的升阻比改善结果。基于这方面考虑,为增加机翼效率,并减轻翼根处的载荷负担,现在的大展弦比飞机,尤其是太阳能动力飞机多采用多机体设计,当双机身间距为0.553 7倍机翼展时机翼刚度性能最佳。对于链翼而言,其基础是多架相同的飞行器,内部的每一架飞机的机翼都可以按照二维无限长假设进行计算,只有外侧飞机的部分机翼考虑升力下降的影响,即每个单体在连接后其机翼都基本满足自身升力需要,载荷传导很小,因此整体的机翼可以在连接机构的有限控制下,保持比较有利且稳定的机翼形状。

即使这样,也不是链翼数量越多越好。美国宇航局太阳神原型机在一次飞行试验中,由于对大气湍流缺乏鲁棒性,导致了的坠毁。换做链翼,虽然能够在一定程度上提高安全性,但连接机构的强度也会受到挑战。在低空,气团的垂直运动对大翼展飞行器有不利影响,过大的翼展会使飞机处于不同的垂直气流下,这会极大地增加连接机构负担,像ELAHA一样采用大柔性机翼虽然可以减弱这种影响,但这种方案会极大地减小机翼投影面积,因而并不适合过多的链翼数量。

由3.1节和3.2节可知,随着展弦比的增大,升力系数、升阻比增大,但趋势均逐渐减缓,保持平飞的巡航速度降低,趋势也逐渐减缓。即增加单元数量,收益呈增长趋势,但理论收益增长的效果逐渐降低。

当实际飞行时,一方面组合体并不是始终保持水平匀速飞行,不理想的姿态控制可能会导致连接机构和机翼承受很大的过载,另一方面低空的湍流随时可能对组合体产生不利的扰动增大过载。考虑以上具体因素时,实际收益并不一定呈现趋势逐渐减缓的增长态势,可能存在一个最优解,最大链翼数量不应高于这个最优解。

4 链翼关键技术

链翼是一个新颖的无人机发展方向,目标直指集群无人机,其研究过程需要突破以翼尖空中对接技术为首的多种关键技术。

4.1 翼尖空中对接

链翼的翼尖连接与分离过程是研究的重点,而在相对于分离更复杂的连接过程中,翼尖涡流的影响,是研究的难点。

第1种方法是减弱翼尖处的涡流强度。现在常用的减小翼尖涡的方法是使用翼梢小翼,结合链翼的特点,可以采用垂直于机翼翼梢小翼。当考虑到两架飞机可能像图22一样沿翼尖旋转时,Gomez等设计了一种类似于副翼的气流调节机构,如图23所示,通过向上偏转气流调节机构,使翼尖涡向机翼内侧移动,这时翼尖处的涡流就会明显减小。

图22 两架飞机沿翼尖旋转Fig.22 Two aircrafts rotating along the wingtip

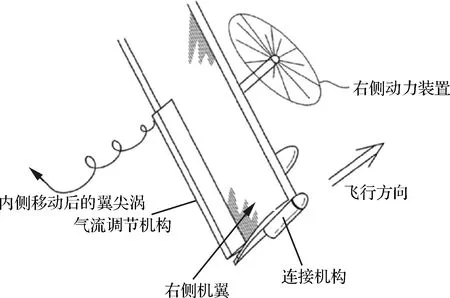
图23 气流调节机构示意图Fig.23 Schematic diagram of airflow adjustment mechanism

第2种方法是寻找最佳的双机靠近方式,可以通过翼尖涡流演示实验,观察各种接近方式的翼尖涡流的稳定性,Magill和Durham通过实验发现,在翼尖的对接过程中,翼尖对接系统在<0°时具有不稳定的非周期模式,在≥2.0°时具有不稳定的振荡模式,当0°<≤2.0°时,具有稳定振荡模式,且高度和速度这些变量对系统的稳定性影响不大。

第3种方法是通过远离翼尖的连接机构连接,而后收紧连接机构使两翼尖完全贴合。“Tip-Tow”项目中,B-29与F-84就曾采用了类似的结构,如图24所示,左侧为B-29的右侧机翼,右侧为F-84的左侧机翼。

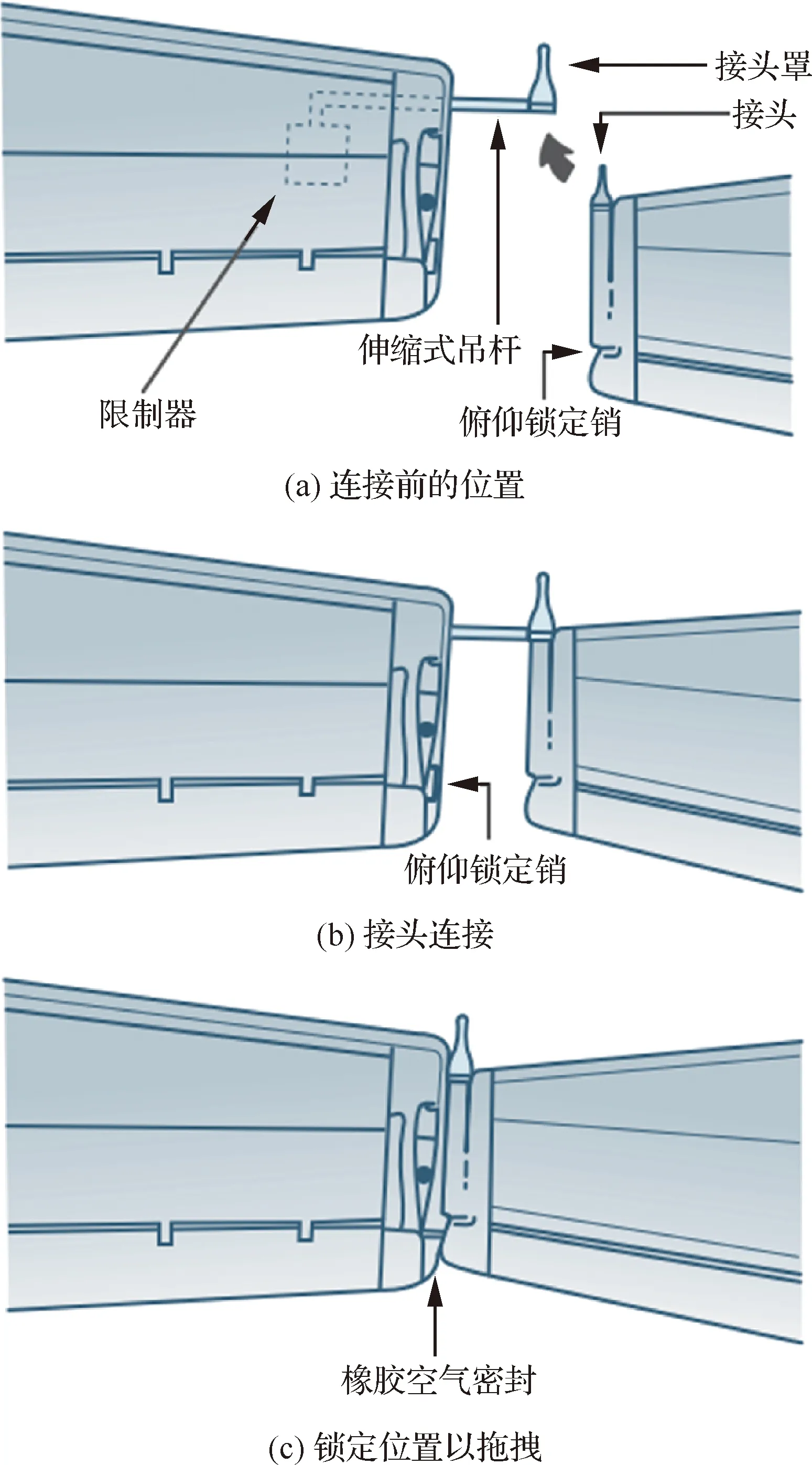
图24 B-29与F-84的翼尖连接过程Fig.24 Wingtip connection process between B-29 and F-84

以上3种方法都能够从一定程度上降低连接过程的难度,对于无人机,具体的对接过程,一般需要计算机自动控制。Cooper和Rothhaar采用美国国家航空航天局的Burnham-Hallock模型。由于翼尖对接的过程不同于简单的航路点跟踪,飞行中的翼尖对接需要具备跟踪任意三维路径的能力。因为目标是受控制和气流扰动双重作用的飞行中的飞机,这可能在靠近阶段出现不可预测的机动。他们根据虚拟引导路径跟踪算法开发出基于视觉或其他方法的制导算法,以真实引导机代替虚拟引导机,路径和速度能够与真实引导机的实际路径和速度相匹配。

4.2 多学科设计优化

翼尖链翼组合涵盖航空、机械、电子、通信等多个科学工程领域,涉及力学、控制、电子等多个学科,具有鲜明的多学科融合的特点。传统的串行飞行器设计模式已经不能满足复杂飞行器的设计要求,需要进行多学科优化设计。近几年,基于伴随方法的梯度类多学科优化设计是较为热门的研究方向,而基于交叉学科变分思想的多学科伴随优化方法也开始在工程领域发挥重要作用。随着人工智能技术的飞速发展,以机器学习为代表的各种智能方法已延伸到飞行器气动、强度、结构设计等各个方面,极大地优化了设计效率和效果。链翼系统层级复杂、规模庞大,不同设计指标对应各学科耦合效应明显。对其研究、设计、优化,只能从复杂系统的角度和层面,建立多学科耦合设计、优化、评价方法体系,为系统的设计开发与优化奠定科学可行的方法论基础。

4.3 超大展弦比柔性飞行动力学

翼尖链翼组合采用链翼模式飞行时,其展弦比非常大,能够超出一般的太阳能无人机。巨大的翼展相对于组合体来说是典型的柔性结构,需以多刚体系统动力学和飞行力学为基础,分析并建立多体柔性组合系统的飞行动力学,才能对大变形和非线性柔性链翼飞行器的运动规律进行研究,或转化为线性问题进行简化的工程求解。

4.4 多机气动耦合和气动弹性抑制

由于结构柔性与飞行气动作用的双重影响,多机气动耦合通过多物理场耦合方法进行计算,多物理场耦合理论及其数值仿真技术成为实现空中飞行以及空中链翼的技术基础,多机气动耦合的风洞试验是重要的验证手段。此外,由于展弦比的增加,机翼结构大柔性会引起几何非线性问题,需要对气动弹性进行抑制以保证良好的飞行姿态。因此,多机气动耦合和气动弹性抑制技术也将是一个重要的关键技术。

4.5 变气动拓扑构型智能控制

链翼飞行受到环境、大展弦比、柔性多体、多物理场耦合等因素的影响,并且根据需要组合和分离,拓扑构型随环境不断变化,控制系统面临的不确定因素增加,需建立基于变拓扑构型气动理论、现代控制理论和人工智能技术相结合的新型多体柔性飞行控制策略和控制技术,以保证链翼飞行达到较好的预期效果。相对于传统刚性偏转舵面,采用翼型变弯度的机翼能够在满足控制需要的基础上进一步提高气动性能。

4.6 空中无线通信组网

翼尖链翼组合的无线网络是飞行系统之间、系统与地面站之间的信息互联形成的通信网络。通信网络拓扑的优化设计是保证多无人机协同安全性和任务执行高效性的重要基础。不同种类的信息对通信实时性和带宽的要求不同,且集群无人机存在个体受损的情况,都要求系统的空中网络拓扑是动态变化的。无线信道是典型的时变多径衰落信道,空中网络技术需要从时间、空间、频率等多维度进行研究,是系统的关键技术之一。

4.7 多任务规划与决策

链翼的多任务、多单元、多时空、多属性带来的多目标优化要求,使任务规划更为复杂,是系统研发和运行维护的重要关键技术之一。任务规划方法一般包括数学规划方法、启发式算法和智能算法,对于分布式任务模型多采用鲁棒性高、计算效率高、可扩展性强的算法和模型,如合同网拍卖模型。翼尖链翼组合无人机系统具有单机、集群、链翼等多种飞行模式,指挥控制系统需要进行更为复杂的多层规划、协调决策。

5 结 论

本文对基于翼尖链翼的组合固定翼无人机的研究进展、理论依据和关键技术进行概述和研究,回答了“为什么链”“如何链”的问题。其中,在研究进展方面,概述了国外早期对翼尖耦合与拖拽技术的研究、德国与美国近年来对翼尖耦合的研究以及中国多个团队在此方面的研究进度。在理论依据方面,对气动特性、飞行性能、链翼数量与效果等进行了讨论,阐述了链翼的优势。在关键技术方面,从空中对接技术、多学科设计优化技术等方面总结了链翼走向成熟需要的技术支撑。

随着控制技术、传感器与测量等技术的进步以及多学科耦合程度的加深,链翼以其相对于单个飞行单元具有更高升限、更长续航,相对高空长航时飞行平台具有更多任务、更加可靠的优势,必将占据无人机领域的一席之地。

未来,搭载了先进太阳能动力系统的链翼无人机,能够稳定对接、及时分离。在链翼状态下,通过传感器的精准快速反馈和控制系统的准确控制,连接结构安全并可靠工作,使链翼组合能够克服一定程度的大气湍流影响。它亦可作为低空伪卫星,在空中执行不间断的军事支援与民生保障等复杂任务,同时向多用户提供多种所需的信息与支援保障服务,满足客户长航时多任务需要。