基于微波相位差测距的叶尖间隙动态测量方法
牛广越,段发阶,周琦,刘志博
天津大学 精密测试技术及仪器国家重点实验室,天津 300072
动叶片作为航空发动机、燃气轮机、烟气轮机、汽轮机等大型旋转机械的核心做功元件,其运行状态参数直接决定了飞机、舰船等重大装备的工作性能。其中,动叶片端面与机匣内壁之间的叶尖间隙参数是影响发动机工作效率及运行安全的关键。航空发动机涡轮叶片的叶尖间隙值通常设计在3 mm以内,并且叶尖间隙每减小0.025 4 mm,燃油消耗率降低0.1%,排气温度下降1 ℃;然而,过小的叶尖间隙会增加叶片与机匣碰撞摩擦的概率,降低发动机安全裕度,甚至导致零部件损坏。叶尖间隙存在最优量值,非接触、高精度、在线的叶尖间隙在线测量方法可为主动间隙控制提供数据支撑,对于发动机高效安全运行具有重大意义。
从20世纪五六十年代开始,伴随着喷气式发动机的发展,基于叶尖传感的叶尖间隙测量技术经过了从“盘车”“动态”“在线”到“在机”几个发展阶段,以及从零部件测试到整机测试的发展趋势,该技术通过将传感器安装在旋转机械机匣上,能够实现叶片尖端距离传感器间隙值的测量,目前主要包括放电探针法、激光三角法、光纤束法、电涡流法、电容法、微波法等。其中,微波法具有以下优势: ① 微波传感器耐1 300 ℃以上高温,抗燃气腐蚀,不易受油污、水蒸气、燃烧产物影响; ② 传感器体积小巧,测量时无机械运动,适用于空间受限的工作环境; ③ 响应速度快、分辨力高、系统带宽可达兆赫兹级别,适用于发动机叶片高转速测试环境。因此,微波式叶尖间隙测量方法是近年来动叶片状态参数测量领域的研究热点。
自1996年起,德国、美国、波兰和俄罗斯的一些航空企业和研究单位先后开展了微波法式叶尖间隙测量方法的研究,已有系统样机在航空发动机上测试应用。2004年,美国普惠公司的Holmquist和Jalbert进行了微波式叶尖间隙测量系统的首次上机试验,获得了测量重复性、一致性、耐久性、线性度、电磁干扰测试等实验结果;2014—2019年,美国佐治亚理工学院的Geisheimer等与Meggit公司合作,在美国国家航空航天局的资助下,将微波式叶尖间隙测量系统应用于航空发动机的结构健康监测和主动间隙控制中,给出了传感器安装方案和部件实验器测试结果,测量精度达到25 μm,典型带宽5 MHz,探头无冷却耐温900 ℃,有冷却耐温1 200 ℃,分析了测量精度影响因素,并指出测试信号可用于叶盘的裂纹诊断;2012年,俄罗斯“雷达技术-2T”有限公司的Maslovskiy等完成了微波式叶尖间隙测量系统在PS-90A2型发动机上的台架试验,分辨力10 μm,精度50 μm,耐温1 700 ℃,耐压20 atm。
虽然部分欧美国家开发出了工程级的微波式叶尖间隙测量系统样机,但其关键技术公开较少,且产品对中国严格封锁。由于研发成本较高、技术难度较大,中国尚无公开的成熟的测量系统原理样机,更未曾在实际航空发动机上开展实验测试。
微波法式叶尖间隙测量方法方法可等效为近程测距雷达,按照测量原理主要分为基于微波相位差测距的叶尖间隙测量方法和基于微波谐振频率测距的叶尖间隙测量方法,然而航空发动机动叶片的工作环境非常恶劣,微波式叶尖间隙测量系统必须在复杂环境下同时具备强抗干扰能力和高精度测量能力,航空发动机内部高温的工作环境容易引起谐振频点的漂移,对比于谐振频率测距法,微波相位差测距法具有更高测量精度,发展更为成熟。
目前叶尖间隙测量领域存在着6个方面的挑战与展望,即:适应恶劣的工作环境、更高的测量精度、高速的信号采集和处理、间隙信号的动态测量、传感器探头的安装和线缆的布置。在间隙信号的动态测量方面,目前微波式叶尖间隙参数的测量和标定过程多基于微波相位差测距原理,开展传感器与被测叶片相对静止的静态实验,是对叶尖间隙参数的静态测量。2019年天津大学的张济龙等利用微带天线式微波传感器,设计了基于位移平台的叶尖间隙静态测量实验,达到35 μm的测量精度;南京航空航天大学的杨季三等提出了一种基于频率域误差模型的微波叶尖间隙传感信号校准方法,提高了标定曲线的线性度,减小了系统测量误差。然而,静态测量方法存在以下难题: ① 微波式叶尖间隙测量系统采用基带式相位解调结构,易受直流噪声干扰,直流偏差会随时间漂移,直接影响叶尖间隙参数的标定结果;② 微波相位差测距原理存在测距模糊问题,当被测叶片旋转时,难以从动态的叶尖间隙相位信号中定位叶片到达的最小叶尖间隙值;③ 叶片旋转过程中,叶尖间隙信号的采样点数时刻变化,直接影响叶尖间隙的测量精度。
针对现有微波式叶尖间隙测量方法的不足,提出一种基于微波相位差测距原理的叶尖间隙参数动态测量方法,构建了测量系统的硬件架构和模块的具体结构,分析了系统的具体工作过程,建立了微波式叶尖间隙测量信号模型,分析了信号的强度和相位特征,仿真了叶片厚度及凹腔对测量信号的影响规律,提出了一种相位区域自适应截取、尺度调整、相关匹配、多项式拟合相融合的技术手段,减小信号处理过程中的随机误差,实现叶尖间隙参数的高精度动态测量,具有重要的工程意义。
1 微波相位差测距原理及信号模型
1.1 微波相位差测距原理
基于微波相位差测距原理的叶尖间隙测量系统隶属于干涉雷达,是一种适用于近程高精度距离测量领域的微波雷达。按照干涉相位解调方式的不同,干涉雷达可分为基带式和外差式,目前基于基带式正交解调器的雷达系统已在航空发动机叶尖间隙测量领域获得广泛应用,其基本工作原理是,单频射频信号源发射出连续的微波信号,经目标物体反射后与参考信号进行干涉解调,解调出的相位差信息即可反映目标物体的位移情况。
如图1所示,测量系统的硬件设备主要包括安装在航空发动机试验现场的微波传感器、信号驱动和调理模块,以及放置在设备间的信号采集模块和计算机。图2更加详细地介绍了测量系统的结构,其中,信号驱动和调理模块主要包括微波信号产生模块、信号功率放大模块、信号接收和混频模块、信号调理模块和环行器。微波信号产生模块提供了频率相同的射频发射信号和参考信号;信号功率放大模块用于放大发射信号和参考信号的功率;信号接收和混频模块将叶片反射回来的信号与参考信号混频,实现基带式正交干涉解调;信号调理模块用于对解调后的正交信号放大和滤波;环行器用于单向传输微波信号,即实现信号从1端口到2端口、2端口到3端口的单向传输。
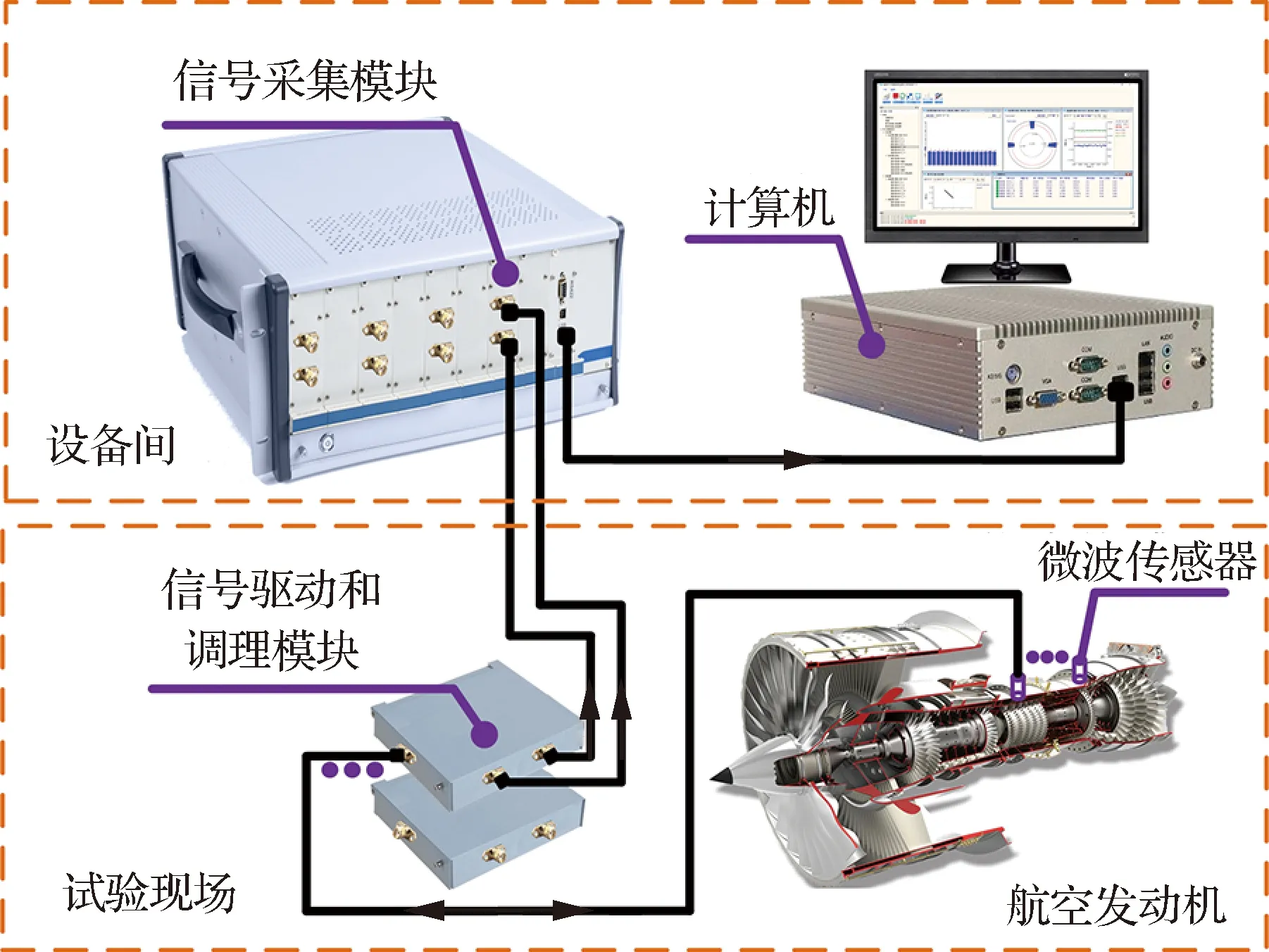
图1 测量系统硬件架构示意图Fig.1 Hardware architecture diagram of measurement system
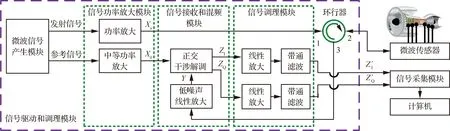
图2 测量系统结构框图Fig.2 Structure diagram of measurement system
系统的具体工作过程为:微波信号产生模块输出发射信号和参考信号,其中,发射信号经功率放大后,通过环行器单向传输到安装在机匣上的微波传感器,传感器探头向动叶片端面投射微波,同时接收反射信号,信号通过环行器单向传输到信号接收和混频模块进行低噪声线性放大,与经过中等功率放大后的参考信号进行正交干涉解调,两路正交信号分别经信号调理模块线性放大和带通滤波后通过信号采集模块传输到计算机,由信号相位值实现叶尖间隙测量。
微波信号产生模块输出的两路信号经过功率放大后,可分别表示为发射信号和参考信号:
=cos(+)
(1)
=cos(+)
(2)
式中:和分别为发射信号和参考信号的幅值;为发射信号和参考信号的频率;和分别为发射信号和参考信号的相位。
微波反射信号可表示为
=()cos(++())+cos(+)
(3)
式中:()cos(++())为叶片端面反射信号,由微波发射信号传播到待测叶片并被反射回微波传感器所产生;()为反射信号的幅值;()为叶尖间隙变化引起的相位差,是瞬变的交流信号;cos(+)为同频干扰信号,由微波在传感器端面的端盖处反射、待测叶片周围静子件杂散反射、射频芯片或环行器隔离度不高等造成;为同频干扰信号的幅值;为传输路径上的累积相位,是随环境温度、振动情况漂移的缓变信号。反射信号分别与参考信号、移相90°的参考信号混频,得到两路正交信号分别为和:
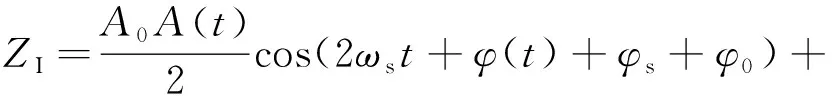
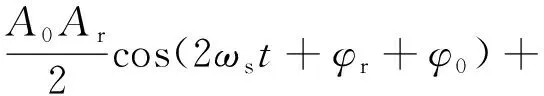
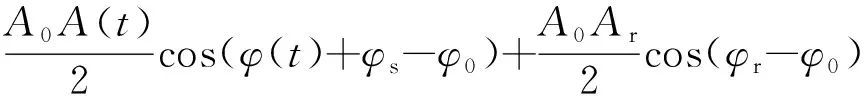
(4)
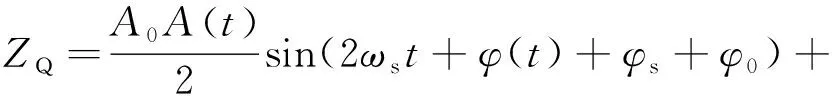
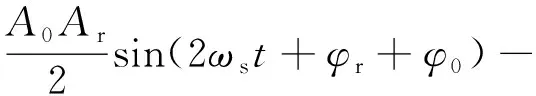

(5)
由式(4)和式(5),信号和中包含了混频产生的频率为射频频率二倍频的分量、含有待测相位差()信息的消除了射频频率的叶片端面反射信号分量、由同频干扰引入的可视为直流的分量。为消除频率为射频频率二倍频和直流的分量,系统采用带通滤波的方法,滤波后的两路正交信号分别为′和′:

(6)
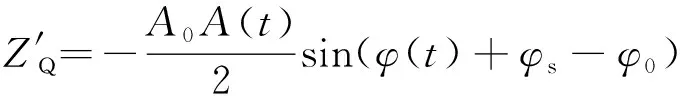
(7)
根据连续波干涉雷达测距原理,叶尖间隙为

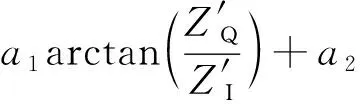
(8)
式中:为射频信号对应的空间波长;、为常数可通过系统标定实验获取。
1.2 叶尖间隙信号模型
在分析微波式叶尖间隙测量系统的工作原理时,式(3),通常将系统接收微波反射信号的过程视为一维点测量,理想的一维点测量是将传感器探头等效为无限细的探针,然而微波式叶尖间隙测量传感器通常具有较大的半功率角,在被测叶片端面具有一定的辐射面积。微波测量信号在叶尖反射的示意图如图3所示,其中,为叶尖间隙最小值,()为当前的叶尖间隙值,为叶片的长度,为叶片旋转角,为叶片旋转频率,为叶片端面横截面的中心点,′为叶片端面横截面的一个边缘角点,为叶片的旋转中心点,为微波信号投射到叶片端面的辐射面积,(,)为辐射面积内一点距离中心点的位置,则(,)∈,=,为叶片旋转时间。

图3 叶尖反射信号示意图Fig.3 Diagram of blade tip reflection signal
因此,若考虑叶片端面的辐射面积,微波反射信号又可表示为
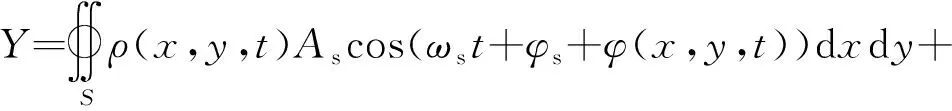
cos(+)
(9)
式中:(,,)为辐射面积内各点的反射系数,微波反射信号经过正交解调和带通滤波后的两路正交信号又可表示为
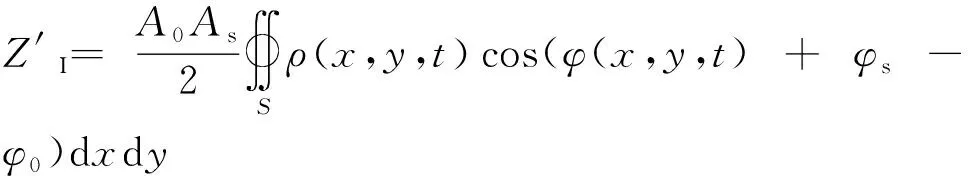
(10)

-)dd
(11)
由式(10)和式(11),叶尖间隙测量信号可通过两路正交信号表示为与叶片旋转角有关的复数函数的形式:
=′+j′=()e-j()
(12)
式中:叶尖间隙测量信号的幅值成分为
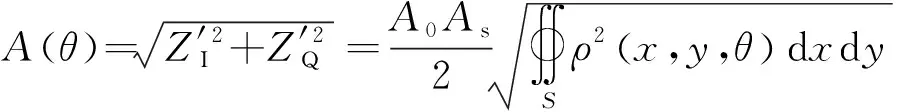
相位成分为()=arctan(′′),是用来标定叶尖间隙的实际测量值。因此,叶尖间隙的测量结果是辐射面积内所有点到传感器探头距离的矢量加权平均值,难以用解析表达式获得其通解,该现象称为空间滤波效应。
由于叶尖间隙的测量范围较小,可使用传感器波束范围内的叶顶面积来估计叶片端面上各点反射系数的变化,当分析叶尖间隙值的动态测量方法时,认为在叶片距离传感器最近位置的附近,叶片旋转角度范围较小时,反射系数基本不变,若叶片端面中心点的间隙值表示为(,0,0)=+-cos(),则辐射面积内其余点(,)的间隙值也是频率为的余弦函数,可表示为(,,)=cos(+)+,因此叶尖间隙测量信号的相位成分可表示为
()=arctan(′′)=′cos(+′)+′
(13)
式中:′、′、′为常数。
2 叶尖间隙信号动态提取方法
2.1 滑动均值滤波及相位区域自适应截取
基于微波相位差测距的叶尖间隙测量系统利用两路正交信号,实现与叶尖间隙值直接相关的相位差的求取,但相位是以360°为周期变化的,由叶尖间隙的计算公式(式(8)),当待测相位差′′的变化范围超过360°时,叶尖间隙值也将呈现周期变化,该现象称为微波式叶尖间隙测量的测距模糊问题。实际上,航空发动机的叶尖间隙设计值通常小于3 mm,24 GHz微波测量系统的无模糊测距范围可达6.25 mm,叶片端面与机匣内壁之间的最小间隙值不会受到该问题的影响,然而如图4所示,当被测叶片旋转时,微波传感器会测到叶片侧面和叶盘的反射信号,由雷达距离方程,接收信号的功率与待测距离的平方成反比,因此,叶片侧面和叶盘的反射信号强度相比于叶尖较小,式(12)中叶尖间隙测量信号的幅值成分呈脉冲形式;此外,由式(12)和式(13),在获取叶尖间隙测量信号的相位成分时,反映了反射信号强度的反射系数参数被消除,同时由于待测距离超过了系统的无模糊测距范围,反射信号与参考信号之间的相位差将以360°为周期变化,难以从动态的叶尖间隙相位信号中定位叶片到达的最小叶尖间隙值。提出了一种微波叶尖间隙信号幅值成分和相位成分相结合的相位区域自适应截取方法,实现了叶片扫过传感器的相位区域截取。

图4 动态叶尖间隙测量信号Fig.4 Dynamic measurement signal of blade tip clearance
2.1.1 滑动均值滤波
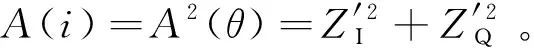

(14)
2.1.2 相位区域自适应截取
由式(12)中叶尖间隙测量信号幅值成分的定义,测量信号的幅值特征不存在测距模糊问题,设叶尖间隙测量信号中的相位成分可表示为微波相位信号()(=1,2,…),与微波相位信号对比,微波强度信号的边沿更加陡峭,更适用于确定叶片扫过传感器前端的信号区域。因此利用了微波强度信号完成包含最小叶尖间隙值的相位区域自适应截取。
由2.1节可知,接收信号的功率与待测距离的平方成反比,因此,不同叶尖间隙下,该脉冲信号的最大幅值变化显著,若采用固定阈值电压法截取强度信号的区域,在同一转速下,截取区域内的数据点数随叶尖间隙值的变化而变化,甚至在叶尖间隙较小时截取不到数据。为保证基于强度信号截取的区域内有足够的、数量恒定的数据进行后续的相关匹配运算,需开展阈值电压值的自适应设定。
利用量程范围内传感器距叶片最远处的微波强度信号峰峰值,预设初始阈值电压值,保证所有叶尖间隙下切割电压均能有效截取信号区间。截取高于阈值电压的微波强度信号,搜索区域内的最大电压值,并以当前圈最大值的恒定百分比作为下一圈的阈值电压,进而实现信号反射强度自适应的区域截取。由于微波强度信号呈现脉冲形式,该百分比的选取一方面需要保证信号的全部顶端特征被完全截取到区间内,另一方面需要避免截取到底部的噪声信号。通常可以根据前期标定实验结果,在40%~80%范围内进行选取。之后采用正交干涉解调方法,求解相位在截取区域内的数值,并进行相位解包裹运算,保证截取区域内的相位连续性,实现相位区域的自适应截取。
2.2 标准信号获取及尺度调整
叶片旋转过程中,采集模块以恒定的采样率对叶尖间隙测量信号进行采样,不同转速下,在自适应截取的相位区域内,叶尖间隙测量信号的采样点数会发生变化,直接搜索截取的相位区域内的最大值,进而获得叶尖间隙测量结果的方法难以保证系统的测量精度。此外,微波传感器具有较大的辐射范围,导致叶尖间隙测量结果是区域内所有点到传感器探头距离的叠加结果,难以获得解析表达式,从而难以找到合适的标准函数(如抛物线函数、高斯函数等)直接对截取的相位区域内的信号进行曲线拟合。由式(13),在最小叶尖间隙值附近,在较小的叶片旋转角度范围内,微波相位信号可近似成余弦函数形式,因此,获取最小叶尖间隙值的位置是实现叶尖间隙信号动态测量的关键。提出一种相关匹配运算预估微波相位信号峰值位置的方法,其中,标准信号的获取是开展信号相关匹配的前提。
在0.5~3 mm的叶尖间隙测量范围内,虽然动态的微波相位测量信号难以解析表达,对于同一端面形貌的叶片,其信号波形形状在不同间隙下基本不变。因此,取一圈内、某一间隙值、较低转速下的微波相位标定信号作为标准信号,完成后续的相关匹配运算。同样,标准信号的获取过程采用了2.1.2节中的相位区域截取方法,但阈值电压值无需反复设定,以最大幅值百分比的方式在10%~30%范围内选取,保证标准信号的数据范围大于测量信号,以开展后续的相关匹配运算。
此外,因为标准信号是在较低转速下获取的,而测量信号对应的转速更高且随着工况实时变化,为开展相关匹配运算,必须将标准信号和测量信号的尺度调整到一致。若以叶片端面宽度对应的数据点数为基准,设信号采集模块的采样频率为,叶片端面的宽度为,叶片的旋转半径为,则当标定过程的转速为时,叶端对应的标准信号数据点数可表示为=()();当测量过程的转速为时,叶端对应的测量信号数据点数可表示为=()(),因此尺度因子可表示为==。设标准信号为(),微波测量信号为(),′为最接近的整数,则尺度调整后的标准信号为′()=(′),其中′=(-1)′+1,其峰值位置设为。
2.3 相关匹配运算
标准信号与微波相位测量信号是线性相关的,可通过信号相关匹配运算,预估峰值位置。由皮尔逊相关系数的定义,标准信号与测量信号之间的相关系数可表示为

(15)
式中:为尺度调整后标准信号的数据点数;为微波测量信号的数据点数;(′,)为′与的协方差;(′)为′的标准差;()为的标准差;其表达式分别为
(′,)=
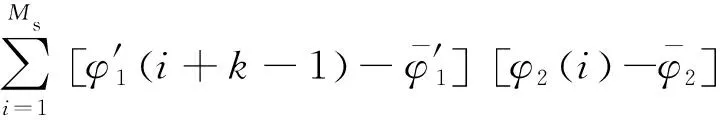
(16)
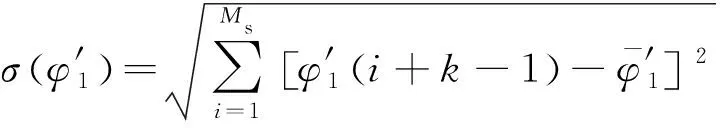
(17)
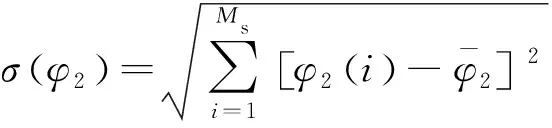
(18)
若()=max时,=,因此,信号峰值位置的预估值为
=-+1
(19)
此时基本确定了自适应截取的相位区域中最大峰值(对应最小叶尖间隙值)的采样点位置。
2.4 峰值区域拟合运算
标准信号与测量信号的相关匹配运算确定了动态叶尖间隙测量信号中叶片距离传感器探头最近时的采样点位置。在最小叶尖间隙值附近,在较小的叶片旋转角度范围内,微波相位信号可近似成余弦函数形式。然而余弦曲线为超越曲线,基于正余弦函数的曲线拟合问题属于非线性回归问题,当将拟合算法移植到下位机时,占用的处理空间较大。实际上,当待拟合的峰值区域较小时,可用抛物线近似余弦曲线。因此,使用基于二次多项式(抛物线)的峰值区域拟合算法,解决微波相位测量信号的线性回归问题。
微波测量系统存在空间滤波效应,叶片端面以外的相位采样点会叠加叶片侧面反射信号,影响叶尖间隙测量结果,选用位于信号峰值位置左右、对应宽度为2 mm的个采样点作为拟合运算数据。设二次多项式形式的标准函数为(),且()=++,则拟合公式为

(20)
峰值参数为拟合曲线的最大值,表示为

(21)
2.5 叶尖间隙参数测量
微波相位信号的峰值参数是与叶尖间隙值直接相关的参数,由式(8),理论上峰值参数与叶尖间隙值是一次函数关系。然而两路正交信号′和′可能存在幅相不平衡因素,使得测量系统获得的相位差信号与叶尖间隙值之间不为简单的一次函数关系,采用基于高次多项式的曲线拟合方法,对0.5~3 mm的叶尖间隙测量范围内的峰值参数进行拟合,分别获得不同端面形貌叶片的叶尖间隙标定曲线,如式(22)所示,进而实现叶尖间隙值的动态测量。
=()
(22)
2.6 方法流程总结
基于微波相位差测距原理的叶尖间隙参数动态测量方法的流程总结如图5所示,主要环节包括:基于转速同步传感器的转速识别、滑动均值滤波、相位区域自适应截取、标准信号获取及尺度调整、相关匹配运算、峰值区域拟合运算、基于标定曲线的叶尖间隙参数测量等。

图5 叶尖间隙参数动态测量方法流程图Fig.5 Flow chart of dynamic measurement method of blade tip clearance
3 仿真及结果分析
3.1 仿真模型
为分析动叶片旋转过程中叶尖间隙测量信号幅值成分和相位成分的特点,利用ANSYS HFSS软件建立传感器和被测叶片的三维电磁场仿真模型,如图6所示,微波传感器采用开放式圆形波导谐振器结构,具有端射、小尺寸、耐高温、结构可靠等性能优点。探头为圆柱体,端面直径9 mm。被测叶片的端面宽度为20 mm,高度为100 mm,旋转半径为150 mm,端面厚度在10 mm以内。仿真时设置微波传感器的最大辐射方向沿端面宽度方向分布,保证微波反射信号的能量最大;叶片的旋转角度以0.5°为步长从-4°扫描到4°,即使在仿真的叶片端面厚度最大时,微波传感器依然可以探测到完整的叶片端面反射信号。分别对不同厚度和凹腔叶片的叶尖间隙测量信号进行仿真,提出了针对不同叶片端面形貌的叶尖间隙动态提取方法。
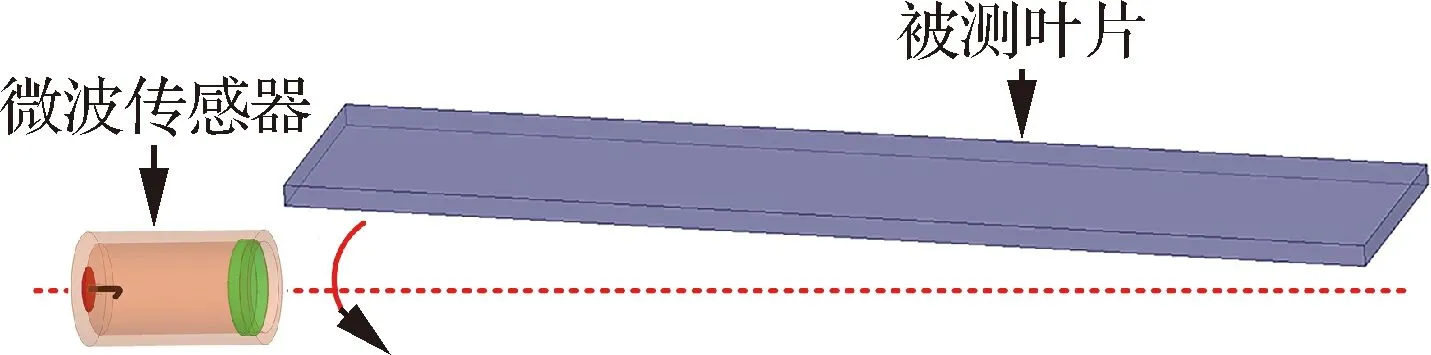
图6 三维电磁场仿真模型Fig.6 Simulation model of 3D electromagnetic field
3.2 单峰式叶尖间隙信号
首先分析了不同厚度叶片的叶尖间隙测量信号特征,依照上文建立的三维电磁场仿真模型,设置叶尖间隙从0.5~3 mm以0.5 mm为步长变化,分别获得了叶片厚度为2 mm、5 mm和10 mm 的信号波形。微波强度信号波形如图7所示,微波相位信号波形如图8所示。
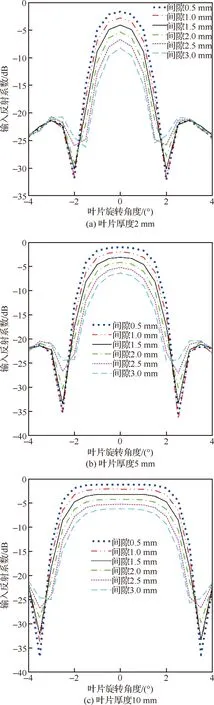
图7 不同厚度叶片的微波强度信号Fig.7 Microwave strength signals of blades of different thickness

图8 不同厚度叶片的微波相位信号Fig.8 Microwave phase signals of blades of different thickness
仿真结果表明,基于微波相位差测距法获得的叶尖间隙测量信号,其幅值成分不存在测距模糊问题,然而相位成分呈现出了以±180°为界限的相位包裹现象,证实了相位区域自适应截取的重要性;对于同一厚度的叶片,其微波相位信号波形的形状在不同间隙下基本不变,证实了取某一叶尖间隙下的微波相位标定信号作为标准信号,完成相关匹配运算的可行性。
由仿真结果,叶片厚度为2 mm和5 mm时,微波相位信号呈现单峰形式,而叶片厚度10 mm时,微波相位信号呈现多峰形式。针对单峰式叶尖间隙信号,其峰值位置存在且唯一,因此在峰值位置附近采用二次多项式拟合算法完成信号峰值参数的提取,将提取的峰值参数代入式(22),即可实现叶尖间隙值的动态测量。
3.3 复杂多峰式叶尖间隙信号
如图8所示,当叶片端面厚度较大时,如10 mm,微波相位信号有两个峰值。叶片增厚会导致双峰现象的出现,原因如下:由图3中待测叶片的几何关系,′>,即叶片端面边缘角点距离旋转中心点的长度要大于叶片端面中心点距离旋转中心点的长度,所以理论上,对于正常叶片,端面边缘的叶尖间隙值比端面中心的叶尖间隙值小,双峰现象是必然存在的。然而微波式叶尖间隙测量方法存在空间滤波效应,叶尖间隙的测量结果是辐射面积内所有点到传感器探头距离的矢量加权平均值,当叶片较薄时,′与差距较小,双峰特征被滤掉,信号呈现为单峰形状,而叶片较厚时,双峰特征才能呈现出来。另外,航空发动机、燃气轮机的涡轮叶片为H形凹腔结构,微波相位信号也会呈现双峰形式。建立了H形凹腔叶片的三维电磁场仿真模型,凹腔结构如图9所示,其位置居中,宽度与叶片端面宽度相等为20 mm,厚度为6 mm,深度为5 mm。叶尖间隙从0.5~3 mm以0.5 mm为步长变化,仿真获得微波强度信号波形如图10所示,微波相位信号波形如图11所示。

图9 H形凹腔叶片的仿真模型Fig.9 Simulation model of H-form concave blade

图10 H形凹腔叶片的微波强度信号Fig.10 Microwave strength signals of blade of H-form concave
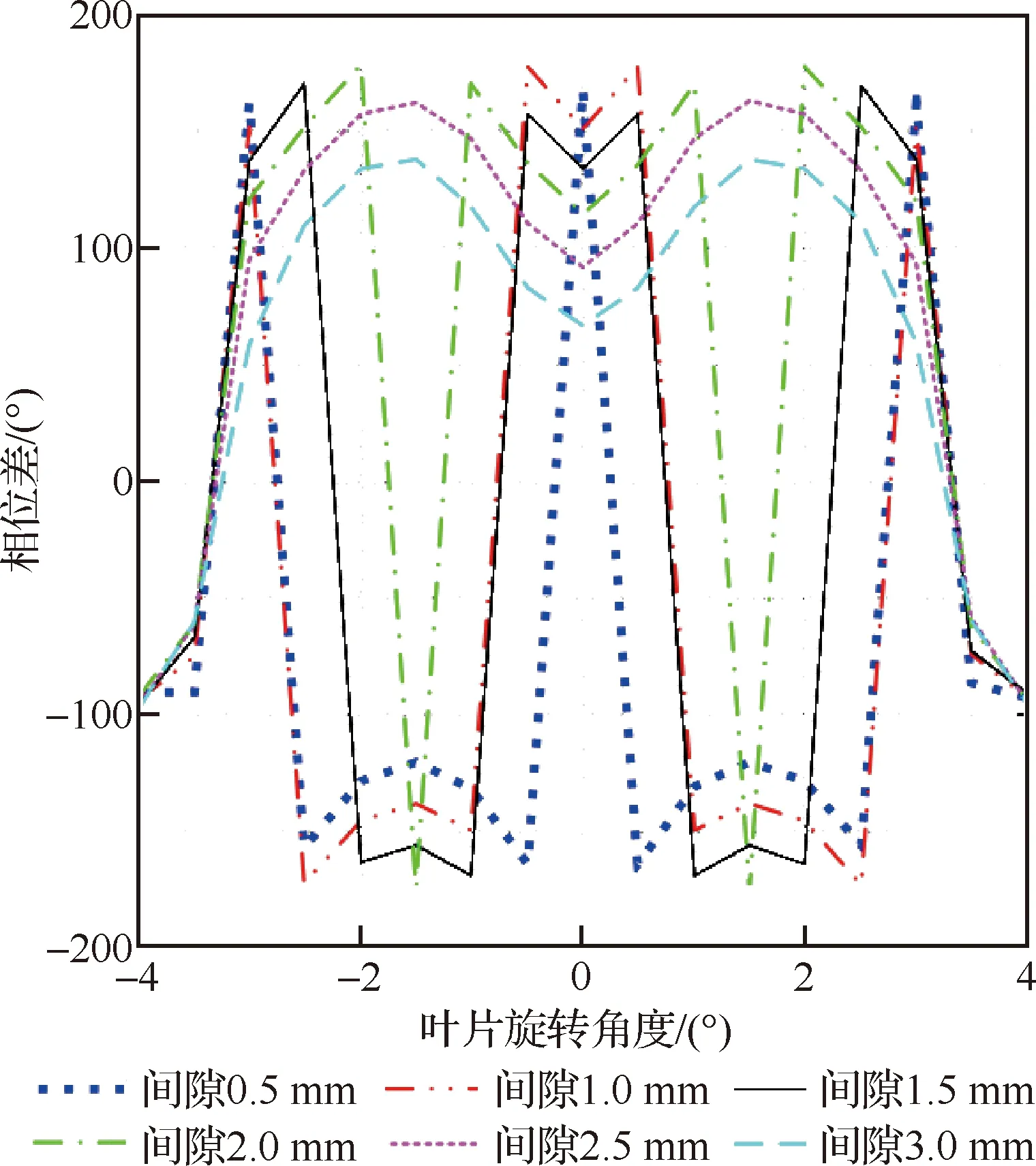
图11 H形凹腔叶片的微波相位信号Fig.11 Microwave phase signals of blade of H-form concave
此外,涡轮叶片端面的密封结构越来越复杂多样,研究人员设计的波状或多凹腔状叶片端面形貌对于提高航空发动机的工作效率具有重要意义。其中,如图12所示,多凹腔形貌将导致叶尖间隙测量信号呈现出更多的峰值数量。设复杂多峰式叶尖间隙信号的峰值数目为,在标准信号获取的过程中,需要确定所有的峰值位置。

图12 多凹腔状的涡轮叶片端面密封结构Fig.12 Squealer-like blade tip seal design
对于尺度调整后的标准信号′(),所有的峰值位置可依次表示为,, …,,使用峰值区域拟合算法,对每个峰值位置附近的数据进行二次多项式曲线拟合,提取到的信号峰值参数依次为、、…、。依据式(23),取各个峰值处测量结果的平均值,减小随机误差,实现复杂多峰信号的叶尖间隙值动态测量,表示为
=[()+()+…+()]
(23)
4 实验及结果分析
4.1 测量系统及实验装置
为验证提出的叶尖间隙参数动态测量方法的有效性和准确性,搭建了测量系统及实验平台,开展了叶尖间隙参数动态测量实验。
研制的测量系统原理样机如图13所示,主要包括微波信号产生模块、信号功率放大模块、信号接收和混频模块、信号调理模块、信号采集模块、环行器和微波传感器。射频信号频率为24 GHz,信号调理模块输出两路正交信号的电压幅值不超过±5 V,信号采集模块的最高采样率为10 MS/s,分辨率为16 bit,由上位机软件进行数据采集,并用MATLAB软件进行数据处理。

图13 测量系统原理样机Fig.13 Prototype of proposed measurement system
搭建了叶尖间隙信号动态测量的实验平台,如图14所示,该平台主要包括叶尖间隙测量系统原理样机、光纤式转速同步传感器、光电前放模块、旋转机械结构、SJ6000型激光干涉仪、计算机、线性电源等测试装置和仪器。

图14 叶尖间隙动态测量实验平台Fig.14 Dynamic measurement platform of blade tip clearance
旋转机械结构与激光干涉仪如图15所示,激光干涉仪作为测量基准,其测量分辨力优于1 nm,测量精度优于1.5 nm (3 mm测量范围内),干涉仪激光头、分光镜、移动反射镜与微波传感器保持共线以避免“阿贝误差”。传感器探头安装在五自由度位移平台上的夹具内,实验前通过调整该位移平台,保证传感器正对待测旋转叶盘的端面,并且传感器的最大辐射方向沿叶片端面宽度方向。待测叶盘由电动旋转台驱动旋转,其速度为50 (°)/s,端面偏心优于5 μm,端跳精度优于15 μm。

图15 旋转机械结构与激光干涉仪Fig.15 Rotating mechanical structures and laser interferometer
待测动叶片如图16所示,从右到左依次为2 mm 厚度、5 mm厚度、10 mm厚度以及H形凹腔形貌的叶片,叶片的外形尺寸参数与仿真一致。

图16 待测动叶片Fig.16 Rotating blades to be measured
理论上,基于微波相位差测距原理的叶尖间隙参数动态测量方法不存在测距盲区,但当待测距离过小时,叶顶位于微波传感器的感应近场区,与传感器的耦合较强,叶尖间隙参数的标定曲线线性度较差,此外,间隙测量系统在航空发动机中应用时,通常会要求设置0.5 mm左右的回缩值,避免传感器探头与叶端碰磨,因此,传感器探头在夹具内的回缩值设置为0.5 mm。
实验过程中,利用五自由度位移平台改变待测叶尖间隙值,并利用激光干涉仪实时得到叶尖间隙基准值,通过改变采集模块的采样率分频数,模拟不同转速不同叶尖间隙下原始叶尖间隙测量信号的获取。
4.2 叶尖间隙参数动态测量实验
在0.5~3 mm的间隙范围内开展以0.1 mm为步长的叶尖间隙参数动态测量实验,激光干涉仪的实时测量值作为叶尖间隙基准值。以采样率分频数设置成360(模拟3 000 r/min的转速)、叶尖间隙0.5 mm、叶片旋转一圈内的信号为例,系统针对4种类型叶片,利用获取的正交信号′和′,求解的微波强度信号()以及微波相位信号()如图17所示。对于某一叶片,将前一圈微波强度信号最大幅值的60%作为阈值电压,实现强度信号及相位信号的自适应截取。
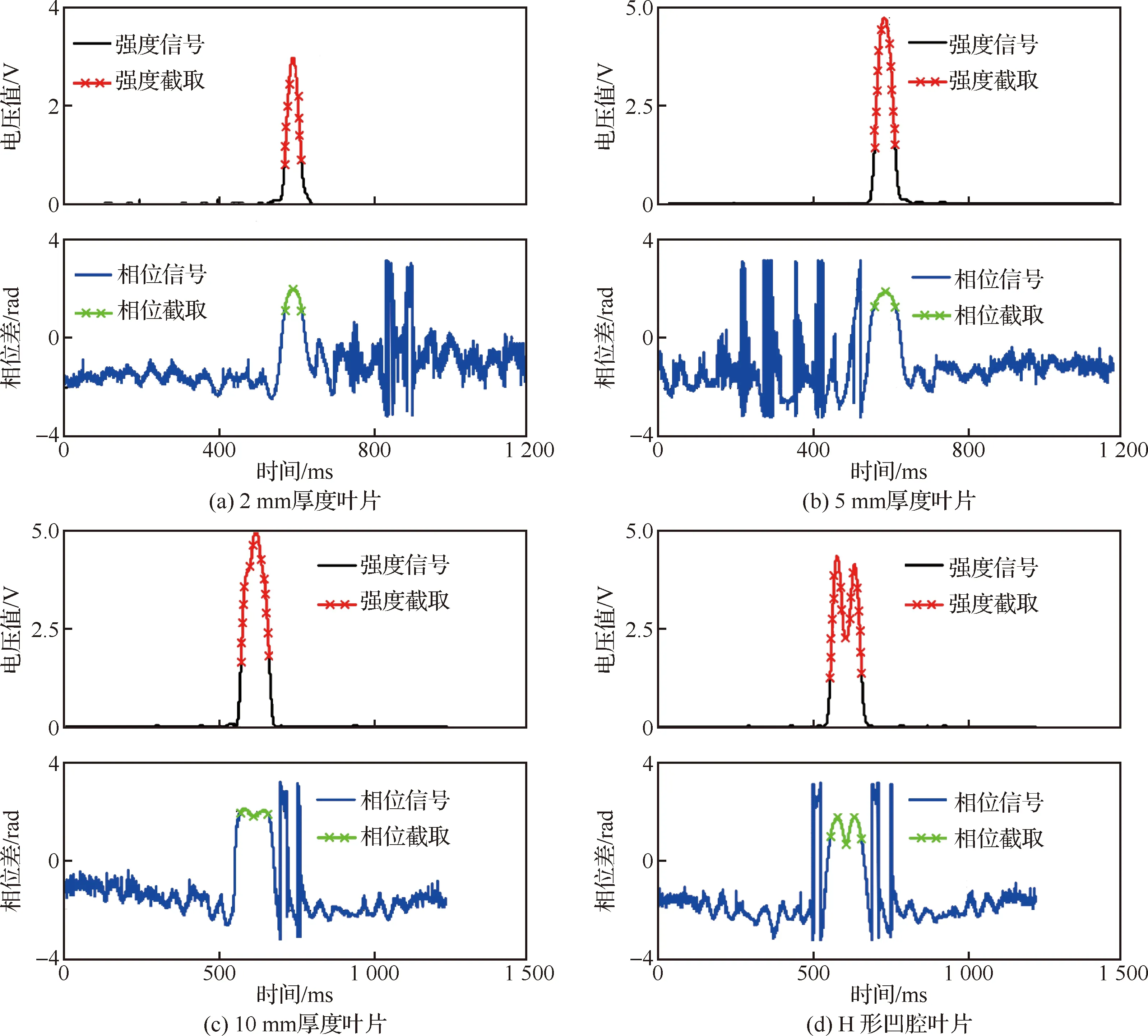
图17 微波强度信号和微波相位信号Fig.17 Microwave strength signals and microwave phase signals
针对4种类型的叶片,以叶尖间隙2 mm、分频数12(模拟100 r/min的转速)条件下获得的微波相位标定信号作为标准信号,如图18所示,记录各个峰值的数据点位置。

图18 标准信号及峰值点位置Fig.18 Standard signals and peak points location
利用标准信号与自适应截取后的微波相位测量信号,开展相关匹配运算,4种类型的叶片在0.5 mm 间隙下的相关系数及相应的数据点位置如图19所示,根据相关系数最大时的数据点位置,按照式(19)计算微波相位测量信号的峰值位置预估值。
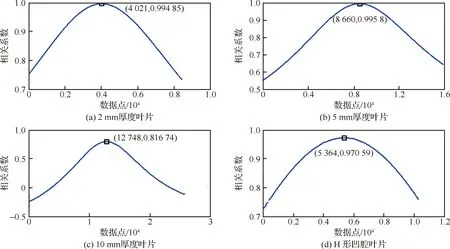
图19 相关系数及数据点位置Fig.19 Correlation coefficient and data points location
在微波相位测量信号的峰值位置左右,选取当前转速下叶片端面上2 mm宽度对应的采样点数,开展基于二次多项式的峰值区域拟合运算,结果如图20所示。
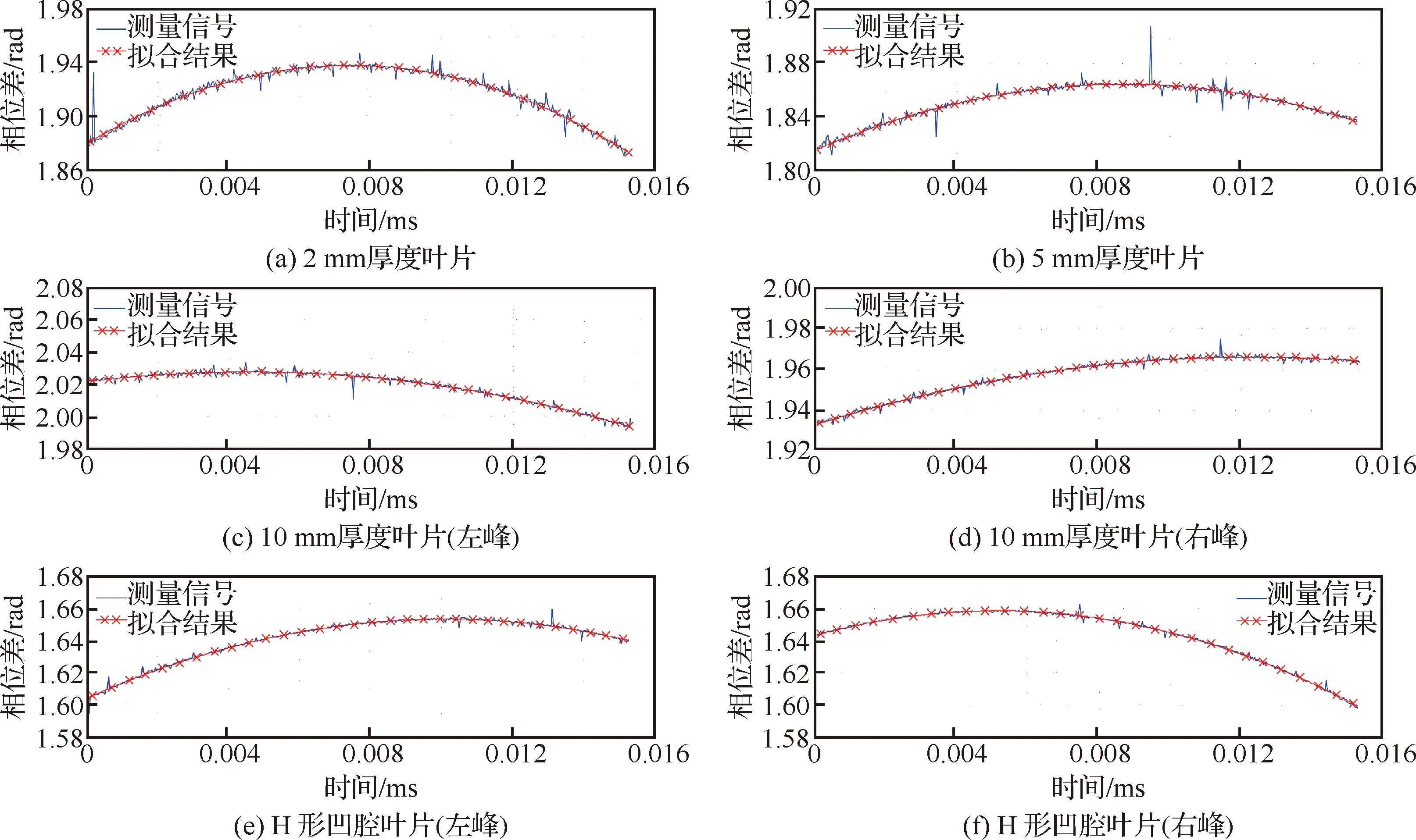
图20 峰值区域的曲线拟合Fig.20 Curves fitting of peak region
针对4种类型的叶片,0.5 mm叶尖间隙下,微波相位测量信号的原始数据与拟合结果之间的残差,如图21所示,由图可以看出,针对峰值位置附近的数据,采用基于二次多项式的线性回归方法,不显示偏差预测,仅能看到随机性,拟合效果较好,可消除测量信号的随机误差。
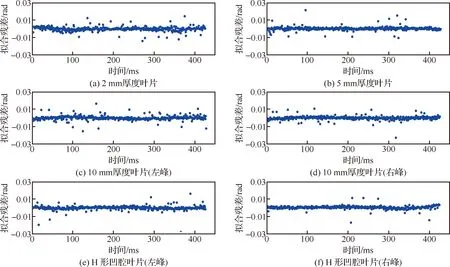
图21 拟合残差Fig.21 Residual error of curve fitting
利用搭建的实验平台获取叶尖间隙标定曲线,得到微波相位信号峰值参数与叶尖间隙值之间的函数关系。在标定实验过程中,以激光干涉仪实时测量值作为基准值,叶尖间隙值从0.5~3 mm以0.05 mm为步长变化,针对4种类型的叶片,在采集模块的采样率分频数12(模拟100 r/min 的转速)条件下分别进行微波相位信号的峰值参数测量。利用多项式拟合算法,采用四次多项式函数,获得了叶尖间隙标定曲线如图22所示。
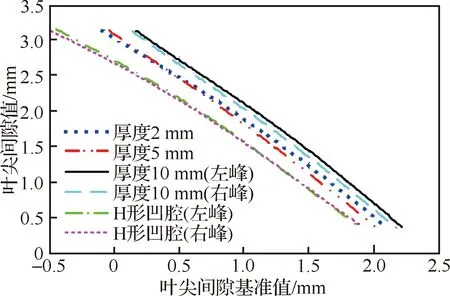
图22 叶尖间隙标定曲线Fig.22 Calibration curves of blade tip clearance
完成了从0.5~3 mm往返3次以0.1 mm为步长的精度评价实验,分频数设置为360(模拟3 000 r/min的转速),通过对比叶尖间隙动态测量值和基准值,实现了对系统测量精度的评价。测量误差分布如图23所示,实验结果表明,研制的微波式叶尖间隙测量系统,采用基于微波相位差的叶尖间隙动态测量方法,在0.5~3 mm量程内测量精度优于40 μm,且该方法适用于不同厚度以及H形凹腔叶片的测量。
此外,为分析转速变化对叶尖间隙参数动态测量方法的影响情况,以2 mm厚度叶片为例,将采集模块的分频数从360~2 880以360为步长增加(实现叶片转速从3 000~24 000 r/min以3 000 r/min 为步长增加的模拟),完成了叶尖间隙从0.5~3 mm以0.5 mm为步长的实验测试。转速变化下的测量误差分布如图24所示,实验结果表明,当采样点数减少时,系统的测量误差增大,但当模拟的叶片转速高达24 000 r/min 时,0.5~3 mm量程内测量精度仍然优于60 μm。

图23 测量误差分布Fig.23 Distribution of measurement errors

图24 不同转速下的测量误差分布(2 mm厚度的叶片)Fig.24 Measurement error distribution for different speeds (blade of 2 mm thickness)
完成了针对不同厚度及H形凹腔叶片的实验验证,但航空发动机真实叶片的厚度常沿叶片弦长方向不断变化,理论上,通过1.2节对叶尖间隙信号模型的理论分析,在不考虑叶片轴向位移、轴向窜动或扭转振动等情况下,对于同一端面形貌的叶片,其信号波形形状在不同间隙下基本不变,因此,针对真实叶片也可用提出的方法进行叶尖间隙动态测量,同理,转速增加也会导致相位信号自适应截取区域内的采样点数减少,进而增大曲线拟合误差,影响间隙值的提取精度。针对真实叶片的实验有待进一步开展,以更加完整地对所提方法进行验证。
5 结 论
1) 提出了一种基于微波相位差测距原理的叶尖间隙参数动态测量方法,从根本上避免了叶尖间隙参数静态测量过程中,直流偏差随时间漂移影响测量精度的问题,开发的系统原理样机经过后续的迭代更新,未来将应用于航空发动机的在机测试,进而能为主动间隙控制提供重要数据支撑,有利于研发人员设计新一代更高效率的航空发动机,具有重要的工程应用潜力。
2) 提出了一种微波叶尖间隙信号幅值成分和相位成分相结合的相位区域自适应截取方法,解决了微波式叶尖间隙测量系统的测距模糊问题,实现了叶片扫过传感器的相位区域截取。
3) 针对微波相位信号难以获得准确的解析表达式,从而难以利用标准函数完成曲线拟合的问题,提出了一种相关匹配运算预估微波相位信号峰值位置的方法,并且在峰值位置附近开展线性的多项式拟合运算,基于叶尖间隙标定曲线,实现了叶尖间隙参数的高精度动态测量。
4) 在实验室搭建了测量叶尖间隙动态信号的实验平台,利用微波式叶尖间隙测量系统样机,开展了叶尖间隙参数动态测量实验。实验结果表明,提出的测量系统和方法,在模拟的3 000 r/min 转速下,0.5~3 mm量程内,不同厚度及H形凹腔叶片的叶尖间隙动态测量精度均优于40 μm。
5) 虽然转速增加会引起采样点数的减少,进而增大系统测量误差,但以2 mm厚度的叶片为例,当模拟的叶片转速高达24 000 r/min时,0.5~3 mm量程内测量精度仍然优于60 μm。

