基于《建筑抗震设计规范》强度包线函数参数取值研究

余文正,吴宗谦,杨瑞欣,兰 香

(1.昆明学院 建筑工程学院,云南 昆明 650214;2.云南国土资源职业学院,云南 昆明 652501)

0 引言

随着减隔震技术在建筑结构中的广泛应用,弹塑性时程分析方法在结构设计中也得到了充分的利用。但是,由于地震波的频谱成分有差异,使得时程分析中不同地震波作用下结构的地震响应有一定差异[1]。与天然波相比,人工波与目标反应谱匹配较好,且离散性要远小于天然地震波[2]。基于此,很多学者采用人工波进行抗震研究[3-5],并且相关国家标准规范也要求采用时程分析时,必须用符合要求的人工合成地震动进行抗震验算[6-7]。不过,当结构进入弹塑性阶段时,结构地震反应的最大值不完全受输入地震动反应谱的控制[8],即便地震动的反应谱非常接近,如果地震动持时不同,其对非线性体系分析的结果也同样有较大的差别[9-10]。由于地震动强度包线函数反映了地震动峰值时刻出现的早晚和能量的集中程度,描述了地震波幅值上升和衰减的过程[11],同时对地震动的强震持续时间和总持时起着控制作用。因此,有学者提出在合成人工地震动时不仅要符合目标功率谱,还要符合目标包线函数[12]。可见,地震动强度包线函数的研究对弹塑性时程分析有着重要的意义。

霍俊荣等[13]根据美国457条强震记录的分析结果,研究了地震动强度包线参数随震级、震中距的衰减规律,并通过回归分析,得到了地震动强度包线参数与震级和震中距的具体关系表达式。屈铁军等[14]及钟菊芳等[15]利用SMART-1台阵记录的312条强震记录,研究了强度峰值因子、衰减系数、上升段和强震平稳段的时间分界点和强震平稳段和衰减段的时间分界点的取值与对应测点的坐标值、测点位置土层厚度的关系,并拟合得到相关表达式。董银峰等[16]利用2011年东日本大地震强震记录,并采用双平稳强度包线模型,建立了加速度时程强度包线函数参数的衰减关系和记录台站的空间分布特征。林建生等[17]探讨了水平加速度峰值和征周期值随强度包线函数参数的变化趋势。肖亮[18]根据美国的304条强震记录,采用三段式强度包线函数模型,建立了我国基岩场地条件下水平向加速度时程强度包线函数参数的衰减关系。张美玲等[19]利用我国2007—2013年之间发生的12次地震的231条基岩强震记录并采用三段式强度包线函数模型,建立了我国基岩场地条件下水平向和竖直向加速度时程强度包线函数参数的衰减关系。

以上关于地震动强度包线函数的研究成果大部分是给出强度包线参数与震中距、震级的关系,需要明确具体的震级和震中距后,才能确定强度包线参数的具体取值,对于大多数建设项目而言,较难获得建设场地的震中距和震级。因此,这些研究成果在大部分建设项目中很难得到实质性的应用。当然,也有部分学者给出了地震动强度包线参数的具体取值,如董娣[20]根据欧洲163组强震记录,分析了地震动强度包线函数的统计特性,并采用胡聿贤和周锡元强度包线模型,根据不同场地类别给出了包线函数参数的具体取值。董银峰[21]利用5 700余条地震记录,分析了强度包线参数的多维相关性及衰减规律,并根据设防烈度、地震分组和场地类别的不同,分别给出了强度包线参数的设计取值建议。李英民等[22]根据703组强震记录的分析结果,研究了地震动强度包线参数随震级、震中距和反应谱特征周期的衰减规律,并根据设防烈度、场地类别和近震远震的不同,给出了一维和三维地震动强度包线参数的建议取值。曹国安等[23]对强度包线函数的研究转化为对地震记录标准差的研究,通过对美国近千条地震记录的标准差的统计计算,给出了具体的强度包线函数。这些关于强度包线参数具体取值的研究成果推广了强度包线函数在人工合成地震动的应用,具有重要的工程意义。

从现阶段研究成果可以看出,地震动强度包线参数的确定均是根据研究者选择的强震记录分析所得。本文将从另一个角度,利用《中国地震动参数区划图》[24](下文简称《区划图》)中采用的地震动参数衰减关系,以及《区划图》中地震动峰值加速度和地震动加速度反应谱特征周期反推不同设防烈度和地震分组对应的震级和震中距,再根据《建筑抗震设计规范》[25](下文简称《抗规》)中各设防水准的峰值加速度确定了《抗规》中不同设计烈度、不同设防水准以及不同地震分组对应地震动强度包线参数的取值。

1 基本思路

强度包线函数采用较常用的三段式模型,包含上升、平稳和下降段,如图1及式(1)所示。

图1 三段式强度包线函数示意图Fig.1 Schematic diagram of three-segment intensity envelope function

(1)

图1和式(1)中f(t)为强度包线函数,参数t1为强度包线平稳段起点,亦即上升段持时,t2为强度包线平稳段终点,ts为平稳段持时,即ts=t2-t1,c为下降段衰减指数,e为自然常数,td为总记录时间。研究表明:参数t1、t2(或ts)和c一般为震级和震中距的函数。

《区划图》给出了中国地震动峰值加速度和中国地震动加速度反应谱特征周期,而这两个参数均是关于震级和震中距的函数。因此,可以根据《区划图》中各地区地震动峰值加速度和特征周期的取值反算各地区对应的震级和震中距,再假定同一地区对应的震中距相同,不同地震水准由震级的大小决定,进而可求得各地区在不同地震水准作用下的强度包线函数取值,基本思路如图2所示。

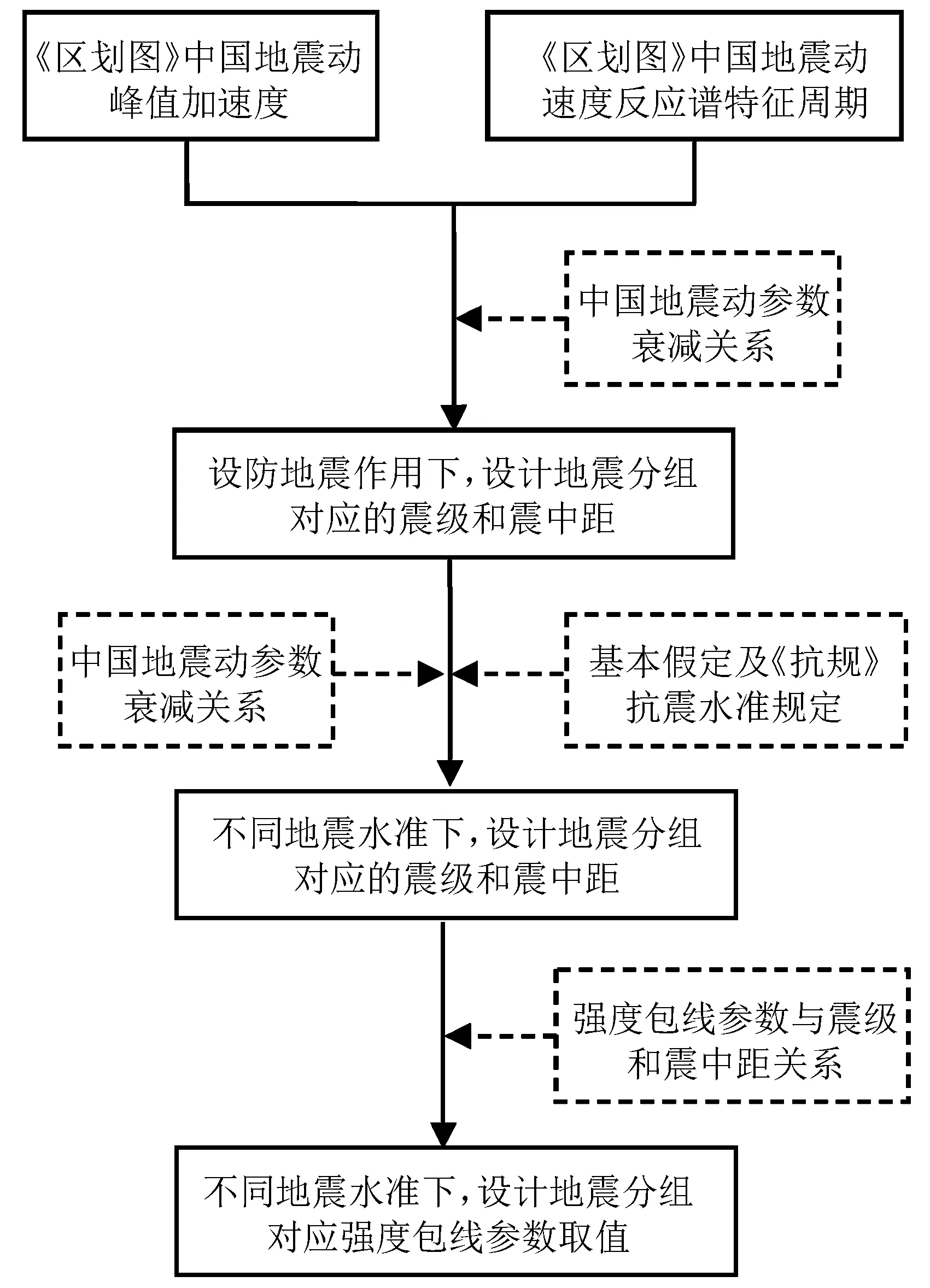
图2 强度包线参数计算流程图Fig.2 Calculation flow chart of intensity envelope parameters

2 设防地震震级和震中距确定

根据文献[26]可知,《区划图》中中国地震动参数衰减关系模型为:

lgY=A+BM+Clg(R+DeEM)

(2)

式中:Y为地震动参数;αE和νE分别为峰值加速度(cm/s2)和峰值速度(cm/s);M为面波震级;R为震中距(km);A、B、C、D和E为回归系数,其数据如表1和表2所列,表中σ为标准差。

表1 αE衰减关系系数Table 1 Coefficients of attenuation relationship of αE

表2 νE衰减关系系数Table 2 Coefficients of attenuation relationship of νE

(3)

将式(2)代入式(3)中,可得

Tg=2π10AT+BTM+CTlg(R+DTeETM)

(4)

式中:AT=Av-Aa、BT=Bv-Ba、CT=Cv-Ca、DT=Dv=Da、ET=Ev=Ea,其数据如表3所列。

表3 特征周期Tg计算系数Table 3 Calculation coefficients of characteristic period Tg

根据文献[27]可知,《抗规》和《区划图》中抗震设防烈度和设计基本地震加速度的对应关系,以及设计地震分组与特征周期对应关系如表4和表5所列。

表4 抗震设防烈度和设计基本地震加速度的对应关系Table 4 Corresponding relationship between seismic fortification intensity and design basic acceleration of ground motion

表5 设计地震分组和特征周期对应关系Table 5 Corresponding relationship between seismic design group and characteristic period

根据表1～5以及式(2)、(3)即可求得各设防地震作用下,不同设计地震分组对应的震级和震中距。例如抗震设防烈度为6度、设计地震分组为第一组时,震级和震中距计算过程如下:

当M<6.5时

(5)

当M≥6.5时

(6)

解上述方程可得:

M=5.96,R=37.26

同理可以得到各设防烈度下设计地震分组对应的震级和震中距,如表6所列。

上述求解过程亦可用图形表示,即在设防地震峰值加速度和特征周期关于震中距和震级的曲线图中,等加速度与等特征周期的交点坐标即为设防烈度和设计地震分组对应的震中距和震级,如图3所示。

图3 震级及震中距图解法Fig.3 Illustration method of magnitude and epicentral distance

表6 设防地震各设计地震分组震级及震中距

Table 6 Magnitudes and epicentral distances of fortification earthquakes in each seismic design group

抗震设计烈度参数类型地震分组设防地震第一组第二组第三组加速值506(0.05g)M5.966.246.48R37.2649.9564.33加速值1007(0.10g)M6.16.386.77R25.4834.9946.59加速值1507(0.15g)M6.196.476.9R19.627.5536.39加速值2008(0.20g)M6.256.617R15.8323.5529.79加速值3008(0.30g)M6.346.747.14R10.9816.6121.26加速值4009(0.40g)M6.46.847.23R7.8512.0815.7注:表中M为面波震级;R为震中距,单位为km;加速度单位为cm/s2。

图3中加速度为0.05g的曲线与特征周期为0.35 s的曲线交点A点,其坐标A(37.26,5.96),表示《区划图》中峰值加速度为0.05g,特征周期为0.35 s,对应的震中距为37.26 km和震级为5.96。

从表6和图3中可以看出,随着震级增加,震中距减小,设防地震峰值加速度增加,亦即设防烈度增加;随着震级和震中距的增加,地震分组增加。

3 不同地震水准震级和震中距确定

在抗震设计时,除了分析设防地震作用在下结构的响应,还需要分析多遇地震和罕遇地震作用下结构的响应,因此,需要明确各地震水准下的震级和震中距。

对于同一地区的多遇地震和罕遇地震而言,其与设防地震的差别主要是震级大小不同,因此,假定在多遇地震和罕遇地震作用下,震中距与设防地震震中距相同。从而根据多遇地震和罕遇地震的峰值加速大小,以及中国地震动参数衰减关系,即式(2),可以确定多遇地震和罕遇地震的震级。

例如,8度(0.20g)罕遇地震,设计地震分组为第二组的震中距和震级计算过程:

先查表6,8度(0.20g)设防地震作用下,设计地震分组为第二组的震中距R为23.55 km,根据假定,罕遇地震作用下,震中距同样取震中距R为23.55 km。

根据《抗规》可知,8度(0.20g)罕遇地震对应的峰值加速度为400 cm/s2,根据式(2)及表1,可得

当M<6.5时

0.561+0.746M-

1.925lg(23.55+0.956e0.462M)=lg(400)

(7)

当M≥6.5时

2.501+0.448M-

1.925lg(23.55+0.956e0.462M)=lg(400)

(8)

解上述方程可得:

M=7.85

因此,8度(0.20g)罕遇地震,设计地震分组为第二组的震中距为23.55 km和震级为7.85。

按照该方法可以求得各水准地震作用下震级和震中距如表7所列。

表7 各地震水准作用下震级与震中距取值Table 7 Values of magnitude and epicentral distance under various earthquake levels

4 强度包线参数取值

现有强度包线参数一般为震级和震中距的函数,因此,根据上节确定的各地震水准下震级与震中距取值,即可确定强度包线参数的取值。本文选取文献[19]中提出的中国大陆地区地震动时程强度包线函数衰减关系来确定强度包线参数取值,其强度包线函数衰减关系为:

lgY=c1+c2M+c3lg(R+R0)

(9)

式中:Y表示强度包线参数t1,ts,c,ts=t2-t1,各参数意义同式(1)和图1中参数意义。

M表示面波震级,R表示震中距,R0表示与震级相关的近场距离饱和因子,取10 km,c1,c2,c3为回归系数,其数值如表8所列,表中σ为标准差。

将表7和表8中的数据代入式(9)中,可以得到多遇、设防及罕遇地震作用下地震动强度包线参数,如表9所列。

表8 强度包线函数相关参数的回归系数Table 8 Regression coefficients of relevant parameters of intensity envelope function

当结构所处地区的抗震设防烈度以及设计地震分组确定后,即可根据表9中强度包线参数生成各个水准地震下的人工波进行抗震时程分析。

5 参数取值规律

为了分析各设防烈度、设防水准和设计地震分组下,强度包线参数的取值规律,本节将表9中数据以图形形式表达,如图4～6所示。

表9 强度包线参数取值Table 9 Values of intensity envelope parameters

从图4～6中可以看出:(1) 总体上,相同设防水准和设计地震分组下,上升段持续时间t1和平稳段持续时间ts随着设防烈度的提高而减小,下降段衰减指数c随着设防烈度提高而增加。根据式(9)可知,上升段持续时间t1和平稳段持续时间ts均是随着震级和震中距的增加而增加,下降段衰减指数c随着震级和震中距的增加而减小,而设防烈度提高时,震级增加,震中距减小。因此,总体上看,震中距对持时的影响要大于震级对持时的影响。

图4 上升段持续时间t1随设防烈度变化关系图Fig.4 The diagram of relationship between duration t1 and design intensity

(2) 同一设防烈度和设计地震分组下,多遇地震、设防地震及罕遇地震对应的强度包线参数各不相同,随着设防水准的提高,上升段持续时间t1和平稳段持续时间ts增加,下降段衰减指数c减小。因此,在抗震分析时,不应对多遇地震作用下生成的地震波进行数值上的缩放来获得设防或是罕遇地震作用所需的地震波。

(3) 同一设防烈度和设防水准下,设计地震分组越高,上升段持续时间t1和平稳段持续时间ts越长,下降段衰减指数c越小。

《抗规》中8度(0.20g)罕遇地震和9度(0.40g)设防地震的峰值加速度相同,均为400 cm/s2,从图7中可以看出,即便峰值加速度相同,设计地震分组相同,设防烈度不同时,其强度包线参数仍然有较大差别,因此,在抗震分析生成人工波时,不能仅依据峰值加速度和设计地震峰值生成人工波,还需要考虑设防烈度的影响。

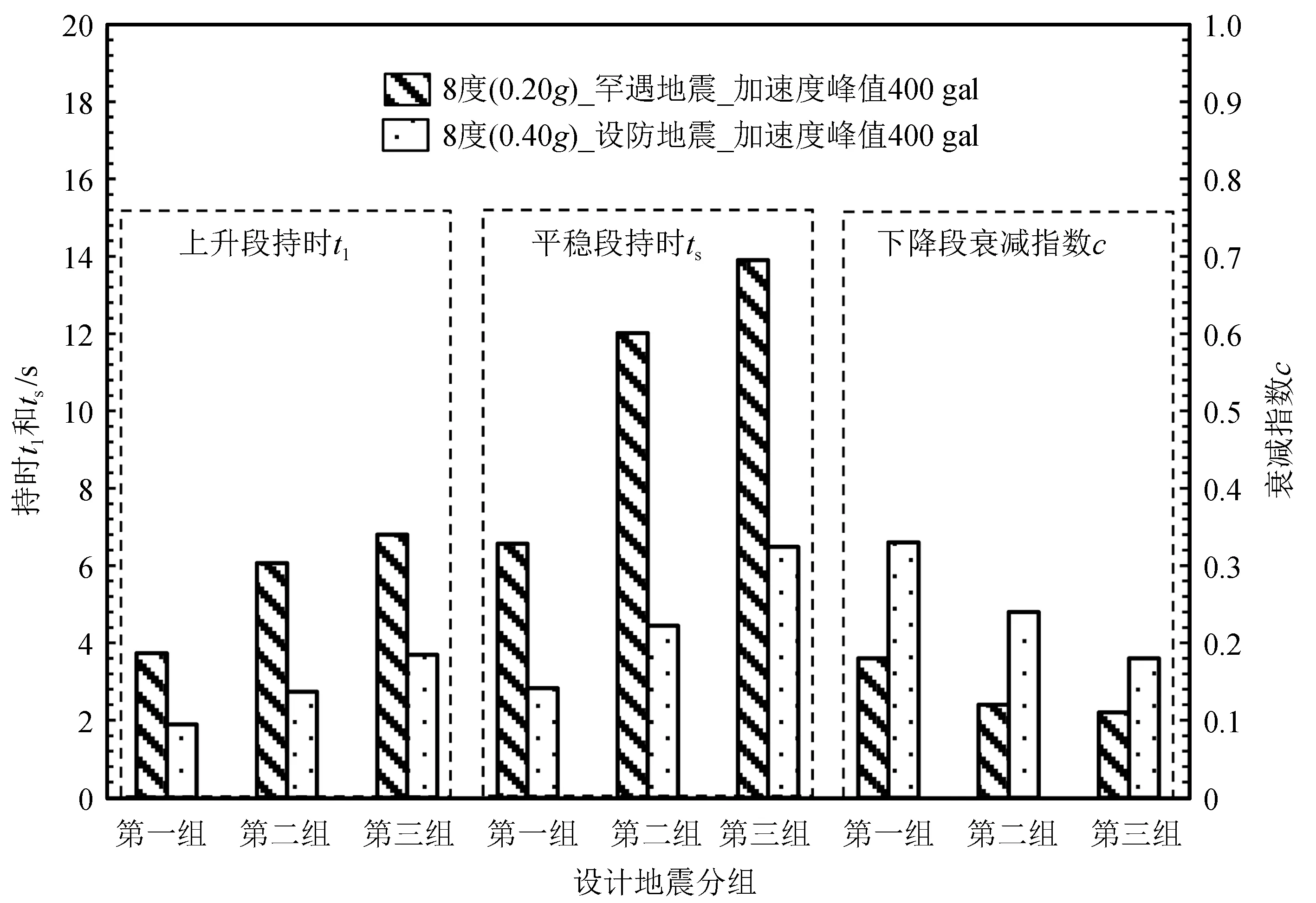
图7 相同峰值加速度和设计地震分组强度包线参数对比图Fig.7 Comparison between intensity envelope parameters with the same peak acceleration and seismic design group

6 结论

利用《中国地震动参数区划图》采用的地震动参数衰减关系,以及《中国地震动参数区划图》中地震动峰值加速度和地震动加速度反应谱特征周期反推不同设防烈度和设计地震分组对应的震级和震中距,再根据《建筑抗震设计规范》中各设防水准的峰值加速度确定了对应的震级和震中距,进而根据地震动强度包线参数与震级和震中距关系计算地震动强度包线参数的取值,为基于强度包线函数生成人工地震动提供参考,并讨论了强度包线参数的取值规律:

(1) 随着设防烈度的提高,加速度时程曲线上升段持续时间t1和平稳段持续时间ts减小,下降段衰减指数c增大;

图5 平稳段持续时间ts随设防烈度变化关系图Fig.5 The diagram of relationship with stable durationts and design intensity

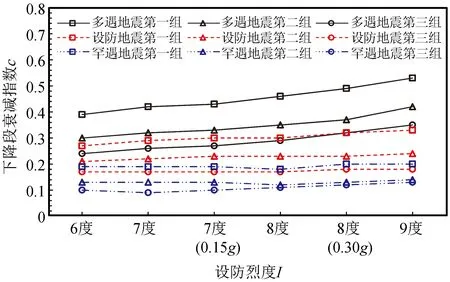
图6 下降段衰减指数c随设防烈度变化关系图Fig.6 The diagram of relationship between attenuation rate c and design intensity

(2) 随着地震水准和设计地震分组的提高,加速度时程曲线上升段持续时间t1和平稳段持续时间ts增加,下降段衰减指数c减小;

(3) 在生成人工地震动时,除考虑峰值和设计地震分组影响外,还需要考虑设防烈度影响。