考虑量测相关性的容积卡尔曼滤波动态状态估计
卢庆春,张俊,许沛东,陈思远,徐箭,柯德平
(武汉大学 电气与自动化学院, 武汉 430072)
0 引 言
电力系统状态估计用于获得电力系统各节点母线的运行状态,是能量管理系统(Energy Management System,EMS)的重要组成部分[1]。电力系统状态估计有两种,包括静态状态估计及动态状态估计[2]。静态状态估计是对电力系统某一时刻的状态进行估计,而动态状态估计则利用当前时刻的状态估计结果对下一时刻状态进行预测,并根据下一时刻实际量测对状态预测值进行修正。因此,相比于静态状态估计,动态状态估计具有预测环节,其可以实时动态地估计系统状态,可以更好地对电力系统状态进行监测。文中研究电力系统动态状态估计。
动态状态估计主要是基于卡尔曼滤波方法进行的[3],国内外对其已经有大量的研究。最开始有文献采用扩展卡尔曼滤波(Extended Kalman Filter,EKF)[4-5]的估计方法,而EKF对电力系统中非线性方程进行展开的方法存在着线性化误差[6]。为了解决EKF方法存在的问题,无迹卡尔曼滤波(Unscented Kalman Filter,UKF)[6-9]被提出,UKF通过对状态量进行离散化采样,然后将采样点代入非线性方程中进行无迹变换,以此计算离散化采样点的离散化函数结果,因而可以避免EKF线性化展开带来的误差。但所有基于UKF的状态估计方法均需要进行无迹变换参数的选取,而参数选取的好坏关系着状态估计结果的准确度。因此,为了克服UKF存在参数选取误差的缺点,有学者提出了容积卡尔曼滤波方法(Cubature Kalman Filter,CKF)[10-13]。文献[10]建立了四阶发电机动态模型,并采用CKF进行发电机的状态估计;文献[11]中提出了可以修正状态预测值的鲁棒CKF方法,并用于估计发电机的状态;文献[12]提出了一种基于Huber M估计的鲁棒CKF方法来应对量测噪声非高斯分布的情况;文献[13]将一种鲁棒的CKF估计方法用于估计同步发电机的状态,其对同步发电机状态模型进行改进,并可以处理输出和输入量测中存在的不良数据,仿真验证算法能明显提高同步发电机的估计精度。上述文献中的误差协方差矩阵均为对角矩阵,通常假设各个量测的误差标准差相同,难免对估计结果造成影响。
然而,量测量间是存在相关性的,且量测误差协方差矩阵是非对角矩阵。文献[14]通过分析变电站内电力系统量测信号的采集过程验证了量测间存在相关性,并用点估计法计算量测相关性矩阵,提出了考虑量测相关性的最小二乘估计算法,仿真验证了考虑量测相关性的最小二乘估计算法相比传统最小二乘估计算法能提高状态估计的精度及计算效率。之后,一些文献开始研究考虑量测相关性的状态估计。文献[15]中考虑了变电站量测相关性,采用两点估计法计算了变电站内所有量测间协方差矩阵,并通过仿真验证考虑量测相关性能提高状态估计的精度;文献[16]分析了最小二乘算法中考虑量测相关性的重要性,通过仿真验证考虑量测相关性能提高状态估计的精度。
目前量测相关性主要应用在静态状态估计中,在动态状态估计中尚缺乏考虑量测相关性的研究。因此,文中提出了一种考虑量测相关性的容积卡尔曼滤波动态状态估计方法。首先对SCADA系统量测量存在的相关性进行分析,然后基于双指数平滑预测过程计算过程噪声协方差矩阵,采用容积变换计算考虑SCADA系统量测相关性的量测误差协方差矩阵,并提出考虑量测相关性的电力系统动态状态估计流程,最后在IEEE-39节点进行仿真验证文中方法动态估计效果。
1 电力系统动态状态估计
1.1 动态状态估计模型
电力系统动态状态估计以卡尔曼滤波为基础, 假设非线性系统的状态转移及量测模型为:
xk=f(xk-1)+qk-1
(1)
zk=h(xk)+rk
(2)
式中xk为k时刻系统状态向量;f(·)为状态转移函数;zk为k时刻系统量测向量;h(·)为系统量测函数;qk-1和rk分别为k-1时刻和k时刻的过程噪声向量和量测误差向量,方差分别为Qk-1和Rk。
(3)

1.2 CKF基本原理
由于CKF算法没有EKF的线性化误差及UKF中选择无迹变换参数带来的参数选取误差,文中基于CKF进行状态估计。CKF状态估计基础是容积变换,容积变换指的是以一个状态量的值作为采样的均值点,依据三阶球面—径向法则[17]产生一些具有相同权值的容积点,然后将每个容积点按照非线性方程进行变换,从而完成对非线性方程的近似。CKF包括预测步以及滤波步,如下所示:
(1)预测
假设k-1时刻系统状态量估计误差方差矩阵为Pk-1。对Pk-1进行Cholesky分解,求得k-1时刻估计误差方差阵的平方根矩阵:
(4)

(5)
(6)
根据式(5)产生的容积点,状态量以及估计误差方差矩阵的预测值可以按下式计算:
xi,k|k-1=f(χi,k-1)
(7)
(8)
(9)
(2)滤波
zi,k=h(γi,k)
(10)
因此,量测预测值为:
(11)
预测量测自协方差矩阵为:
(12)
Tk=Sk+Rk
(13)
状态预测及量测预测的互协方差矩阵为:
(14)
卡尔曼滤波增益矩阵可以按下式计算:
(15)
因此,k时刻的状态估计值以及估计误差方差矩阵可以表示为如下形式:
(16)
(17)
2 考虑量测相关性CKF动态状态估计
结合目前电网中广泛配置的SCADA量测,文中研究SCADA量测间的相关性。电力系统动态状态估计的量测方程h(x)为:
(18)
式中Pi为节点注入有功功率;Qi为节点注入无功功率;Pij为支路有功功率;Qij为支路无功功率;Vi和Vj为节点电压幅值;Gij为节点导纳矩阵i行j列元素电导部分;Bij为节点导纳矩阵i行j列元素电纳部分;θij=θi-θj为支路两端节点相角差;gij为节点导纳矩阵i行j列元素互电导部分;bij为节点导纳矩阵i行j列元素互电纳部分;y为支路对地导纳。
2.1 SCADA系统量测相关性分析
对于SCADA系统,状态估计所用的量测量包括节点电压幅值、节点注入功率(有功/无功)、支路潮流功率(有功/无功)。除去节点电压幅值,其余量测由电力系统中间装置对互感器量测进行中间计算得到。文中假设每个节点或线路单独安装了互感器。
假设互感器电压幅值量测量为:
(19)

假设中间量测电压相角差为:
(20)
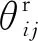
因此,式(18)可以写成:
(21)
由式(21)可知,Pi、Qi、Pij、Qij均受互感器量测误差εi和εij影响,因此这些量测量间存在着相关性。Pi和Pj由于受εi和εij影响,两个量测量间也存在相关性,其他量测间的相关性同理可知。
因此,SCADA系统量测量间存在相关性。误差协方差矩阵Rk是非对角阵,对角线元素表示量测量的误差自方差,非对角线元素表示的是各量测量之间的误差互方差。Rk可以表示为:
(22)
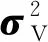
(23)
(24)
2.2 过程噪声协方差矩阵Qk
过程噪声方差矩阵Qk关系到状态估计结果的精度,因此Qk的合适选取十分关键。第2.2节采用的过程如下:
(1-α)3xk-3|k-4+bk-1+(1-α)bk-2+(1-α)2bk-3
(25)
对bk-1进行展开得到:
(26)
同理,也可对bk-2、bk-3及bk-n进行展开。
由状态转移方程可知,k时刻的系统状态预测值与k时刻之前的所有时刻均有关,且受邻近时刻的影响较大。因此,过程噪声是动态变化的,随系统状态的变化而时变。
由于α和β取值均为[0,1],当系数次数越高,取值越小。当相邻时刻系统状态变化不大时,其差值很小,为加快求解效率,取状态转移方程为:
(27)
根据误差传递规则,可以求得过程误差协方差矩阵为:
(28)
2.3 考虑量测相关性的量测误差协方差矩阵Rk
误差协方差矩阵Rk中非对角元素体现着量测间的相关性,因此考虑量测相关性的状态估计不能假设Rk为一个特定矩阵。由于容积变换方法能够根据自变量的协方差矩阵容易得到因变量的协方差矩阵,因此,文中基于容积变换法计算Rk。
假设互感器量测的电压幅值和相角差量测向量为:
(29)
向量维度为m1。求解互感器量测量的协方差矩阵为:
Hk=E[(Lk-E(Lk))(Lk-E(Lk))T]
(30)
依照第1节中的容积变换思想,求取2m1个容积点ζi,k。
(31)
(32)
其中,{1}i为矩阵{1}的第i个列向量{1}如下所示:
(33)
将容积点代入量测方程,得到SCADA系统的量测量如下:
Zi,k=h(ξi,k)
(34)
量测均值为:
(35)
取量测量误差协方差矩阵近似为:
(36)
2.4 考虑量测相关性CKF动态状态估计流程
文中考虑量测相关性的容积卡尔曼滤波方法流程如下:
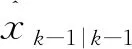
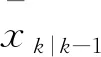
(4)根据k时刻互感器量测得到的互感器量测向量Lk,通过容积变换方法求得容积点,通过式(34)~式(36)计算量测误差协方差矩阵Rk;
(6)计算状态预测及量测预测的互协方差矩阵Ck;
(7)计算卡尔曼滤波增益Kk,k时刻状态估计值,以及k时刻状态协方差矩阵Pk;
(8)更新X_est,循环步骤(1)~ 步骤(8),进行动态状态估计。
3 算例分析
3.1 算例设计
为验证文中所提考虑量测相关性的动态状态估计算法的估计效果,第3.1节在IEEE-39节点系统(图1)上进行了仿真分析,并和不考虑量测相关性的CKF方法进行对比。通过在DIgSILENT上进行时域仿真产生一系列采样数据,在Matlab上进行动态状态估计。时域仿真时,对系统设置短路故障,在t=0.18 s时,节点16发生接地短路故障,并在t=0.36 s清除故障,时域仿真时间为10 s。
对于不考虑量测相关性的CKF方法(记为传统CKF),其量测误差协方差矩阵的对角线元素取为文中量测误差协方差矩阵Rk对角线元素,状态转移方程采用文中状态转移方程。
仿真分为两种情况:(1)各个互感器电压幅值量测误差及中间量测电压相角差的误差均服从均值为0、方差为10-4的正态分布,即εi~N(0,10-4),εij~N(0,10-4),i和j为不同的任意节点;(2)各个互感器电压幅值量测误差及中间量测电压相角差的误差均服从均值为0、方差为10-5的正态分布,即εi~N(0,10-5),εij~N(0,10-5),i和j为不同的任意节点。
互感器量测电压幅值由节点电压幅值真值叠加εi得到,中间量测节点电压相角差量测由节点电压相角真值做差得到相角差后,再叠加εij得到。SCADA系统的其它量测量Pi、Qi、Pij和Qij,由式(18)计算得到。
仿真采用平均绝对误差反映估计值误差的实际情况,平均绝对误差(MAEk)定义如下:
(37)

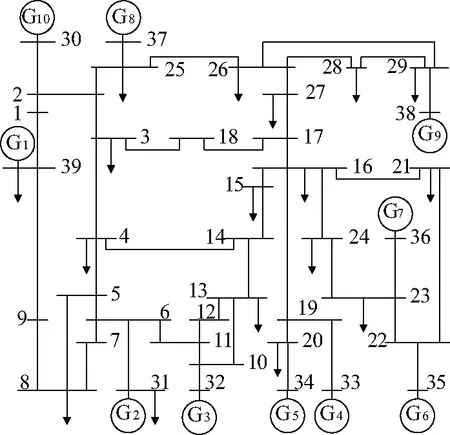
图1 IEEE-39节点系统
3.2 结果分析
假设SCADA系统数据的刷新频率为5帧/s,即1 s采样5个数据,采样间隔为0.2 s。在短路故障清除后,对仿真数据进行采样,跟踪系统故障恢复的动态过程。为了获得具有统计意义的结果,进行了50次蒙特卡罗模拟,取50次模拟的平均值作为最终估计结果。以节点16为例,分析动态状态估计结果。
(1)情况1:节点16上的电压幅值和电压相角的估计结果分别如图2和图3所示。各个时刻所有节点电压幅值和相角的平均绝对误差比较结果分别如图4和图5所示。

图2 节点16上电压幅值估计结果比较(情况1)

图3 节点16上电压相角估计结果(情况1)
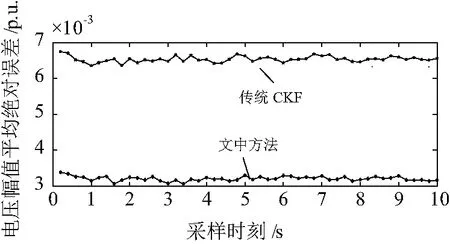
图4 电压幅值平均绝对误差比较(情况1)

图5 电压相角平均绝对误差比较(情况1)
从图2可以看出,在故障恢复过程中,两种方法在节点16的电压幅值估计值均能跟随电压幅值的真值而变化,但文中方法的估计曲线更贴近真实曲线。从图3可以看出,两种方法在节点16的电压相角估计值均能跟随电压相角的真值而变化,相比电压幅值,由于相角值较大,两种方法的估计曲线几乎重叠,但从局部放大图仍然可以看出文中方法相角估计曲线更贴近相角真实值。从图4和图5的平均绝对误差曲线可以看出,在各个采样时刻,无论是电压幅值还是电压相角,文中考虑量测相关性的方法平均绝对误差均小于不考虑量测相关性的方法,这是由于量测误差方差矩阵中的非对角线元素对状态估计预测值具有修正作用。
(2)情况2:节点16上的电压幅值和电压相角的估计结果分别如图6和图7所示,各个时刻所有节点电压幅值和相角的平均绝对误差比较结果分别如图8和图9所示。

图6 节点16上电压幅值估计结果比较(情况2)

图7 节点16上电压相角估计结果(情况2)
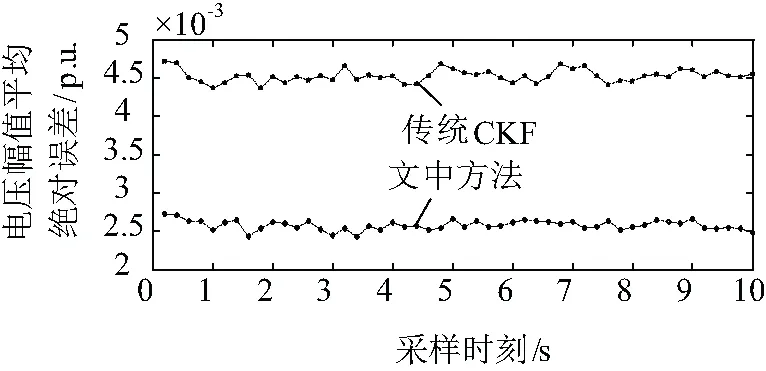
图8 电压幅值平均绝对误差比较(情况2)
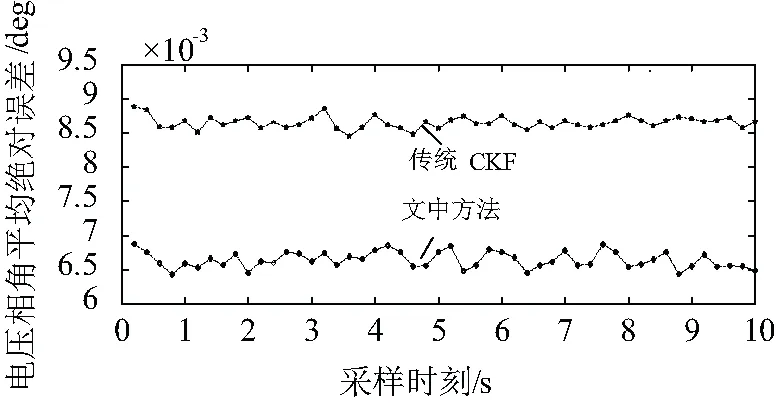
图9 电压相角平均绝对误差比较(情况2)
当互感器节点电压幅值量测的误差方差及中间量测节点电压相角差的误差方差由10-4变为10-5时:从图6和图7可以看出,文中方法在节点16上的电压幅值和电压相角估计值仍能较为准确地跟随电压幅值和相角的真值动态变化。对比图4和图5的平均绝对误差曲线,从图8和图9可以看出,两种方法的平均绝对误差均有所减少,说明互感器量测值误差大小会对估计结果产生影响,且互感器量测值误差方差越小,估计结果越精确;在各时刻,文中考虑量测相关性方法的平均绝对误差仍小于不考虑量测相关性的方法。
综上可知,在电力系统动态状态估计中考虑量测相关性是必要的;且将考虑量测相关性的CKF方法与不考虑量测相关性的CKF方法相比,前者比后者更能提高状态估计的精度。
4 结束语
基于工程实际中SCADA量测量间存在相关性的实际情况,文中提出了一种考虑量测相关性的容积卡尔曼滤波动态状态估计方法。在IEEE-39节点系统进行的仿真验证了在电力系统动态状态估计中考虑量测相关性是必要的,文中方法能够显著提高电力系统动态状态估计的精度,且能为工程实际中进行动态状态估计研究提供一定的借鉴意义。然而文中的研究仅考虑了SCADA量测相关性,随着电力系统广域量测装置PMU的增多,下一步将要研究考虑混合量测相关性的电力系统动态状态估计。

