汽车与行人碰撞中大灯断裂失效模拟的研究

常浩，郑颢，蔡永周，罗芬，孙丽，潘周锐

（广州汽车集团股份有限公司汽车工程研究院，广州511434）

前言

据统计，我国乘用车与行人碰撞事故占总事故比例近20%，其中行人死伤人数占交通事故死伤总人数的30%，CIDAS（China in-depth accident study）工作组通过对大量的行人碰撞交通事故数据进行分析，发现行人与车辆碰撞事故中行人受到损伤概率最大的部位是行人的头部和下肢，且由于人体下肢相关结构难以修复，下肢损伤往往会造成终身残疾，头部损伤通常会造成人员伤亡。因此车辆对行人碰撞保护研究多集中于行人头部和下肢。C-NCAP（China new car assessment program）从2018版开始将行人保护评价纳入新车安全评价规程，在产品设计开发阶段，主机厂通常采用CAE仿真技术开展行人保护优化设计。车辆与行人的碰撞事故主要发生在汽车的前端，对汽车前端结构进行合理的优化设计可降低车辆对行人的碰撞损伤。针对行人下肢的碰撞位置，车辆前端主要是前保险杠、前格栅、前大灯等非金属材料结构为主，它们在行人下肢碰撞中通常会发生断裂失效。为通过CAE数值模拟计算，得到更为准确的汽车结构安全设计方案，须对非金属材料的断裂失效行为进行预测。考虑不同应变率和应力状态的聚合物塑料材料失效模型的准确建立是行人保护动态仿真领域的难点。

汽车前大灯由于材料较强，整体刚度大，在车辆与行人的碰撞过程中，会对行人下肢造成较大的损伤，因此在前大灯结构设计过程中须对大灯支架进行压溃设计，使其在碰撞过程中发生断裂失效，减小对行人下肢的冲击载荷。为使CAE能准确模拟大灯支架的断裂失效，须对大灯材料的断裂失效模型进行研究。汽车大灯灯壳主要采用玻纤增强的PP塑料，其具有较高的弹性模量和抗拉强度，但其延展性较差，断裂延伸率通常在2%~3%左右，较易发生断裂失效。本文中以某车型大灯灯壳PP-GF30材料为研究对象，通过不同应变率和应力状态的材料表征试验和仿真对标，建立了PP-GF30材料的失效模型。

1 MAT_SAMP-1失效模型

塑料材料常见拉伸应力-应变曲线如图1所示。塑料材料在小载荷下一般具有线性黏弹性（段）；随载荷增大开始呈现微弱的非线性，在屈服点处达到屈服应力σ，点后诱导塑性变形，产生结构演变，材料抵抗塑性流动能力降低，发生应变软化（段）；随即试样出现塑性不稳定型，应变增加而应力基本不变（段）；随着变形的进一步增大，材料发生应变硬化（段），最终在点达到拉伸极限强度σ，材料内部分子链断裂，发生断裂失效。

图1 塑料材料常见拉伸应力-应变曲线

材料由弹性阶段进入塑性阶段的条件称为屈服准则。塑料材料的屈服行为具有静水压力相关性，传统的静水压力无关的屈服准则，如Tresca屈服准则、Von Mises屈服准则等并不能准确描述塑料材料的屈服行为；同时塑料材料在注塑加工过程中会产生一定的各向异性，尤其是以塑料为基体的复合材料，其各向异性更加明显。因此塑料材料的屈服准则须同时受到静水压力和各向异性的影响。

Kolling等基于LS-DYNA软件开发了一种适用于塑料材料的MAT_SAMP-1（semi-analytical model for polymer）本构模型，该模型采用Drucker-Prager屈服准则，修正了Von Mises屈服准则，对材料动态力学模型进行解析，可采用两种不同形式的压力相关项表征塑料材料的屈服准则。MAT_SAMP-1材料本构模型中采用的屈服准则为应力状态相关的，屈服函数定义为第一不变量（静水压力）和第二不变量（Von-Mises等效应力）的二次函数，其压力屈服面表达式为

式中：为Von-Mises应力；、、为通过材料的单向拉伸、单向压缩和剪切试验求得的屈服应力值函数；为静水压力。

MAT_SAMP-1失效模型可用来描述塑料材料在试验过程出现的弹塑性和断裂行为，断裂表征不仅能将一个固定值作为失效准则，也可以输入一条随应变率变化的曲线作为失效准则，允许考虑拉伸、压缩、剪切等多种工况的失效应变来建立失效应变与应力三轴度的关系曲线，与传统的MAT_PIECEWISE_LINEAR_PLASTICITY材料相比，能更全面考虑不同应变率和应力状态对塑料材料弹塑性和失效断裂力学性能的影响。对塑料材料的复杂力学性能描述更加全面，使用更便捷，已经得到较为广泛的实际应用。

图2为MAT_SAMP-1断裂失效模型的开发流程图。通过静态和动态力学试验，可获得材料的弹塑性和断裂力学行为。弹性行为包括计算弹性模量和泊松比，塑性行为包括计算不同应力状态下塑性应力-应变曲线。静态下的失效准则通过准静态各应力状态试验，建立相应的仿真模型，采用仿真对标方法确定断裂点的等效失效应变和应力三轴度的关系，通过动态单向拉伸试验确定等效失效应变和应变率的关系，模拟动态下的失效准则。

图2 MAT_SAMP-1失效模型开发

2 材料力学试验与仿真

2.1 材料表征试验

由于塑料材料注塑加工工艺对材料力学性能会产生影响，故试验直接从如图3所示的汽车前大灯灯壳上平整区域裁剪出PP-GF30材料样品进行试验。材料试验参照ISO 8256—2004和ISO 178—2010测试标准进行。

图3 汽车前大灯

材料表征试验包括单向拉伸、双向拉伸、面内压缩、剪切和穿孔试验，如表1所示。单向拉伸试验包括静态和动态工况下共6个应变率（0.001、0.1、1、20、100和400 s）的力学试验，用于确定材料应变率效应，其中0.001和0.1 s在万能试验机上完成，1、20、100和400 s在高速拉伸试验机上完成。双向拉伸、面内压缩、剪切和穿孔试验用于失效准则的构建。为保证试验结果的一致性，各应变率重复3次试验。所有试样从前组合灯本体上裁切而成，图4示出各试样形状和尺寸。各试样试验后图片如图5所示。

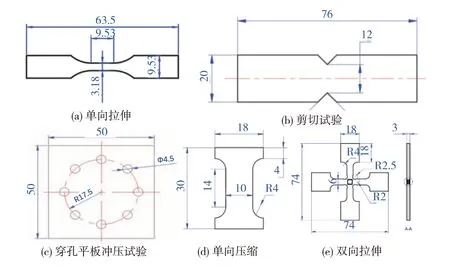
图4 试验样件形状和尺寸

图5 试验后图片

表1 材料试验矩阵

采用下式对拉伸和压缩试验数据进行处理：

式中：为真实应变；为真实应力；为塑性应变；为工程应变，采用非接触测量方法计算得到；为工程应力，由载荷除以试件初始横截面积计算得到；为弹性模量。

采用下式对剪切试验数据进行处理：

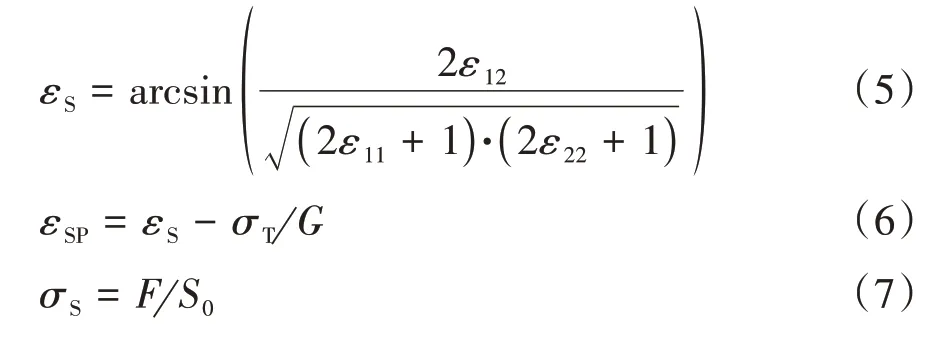
式中：为剪切应变；、、为3个方向应变，采用非接触测量方法计算得到；为剪切塑性应变；为剪切模量；为剪切真实应力；为载荷；为剪切截面积。

采用下式对双向拉伸试验数据进行处理：

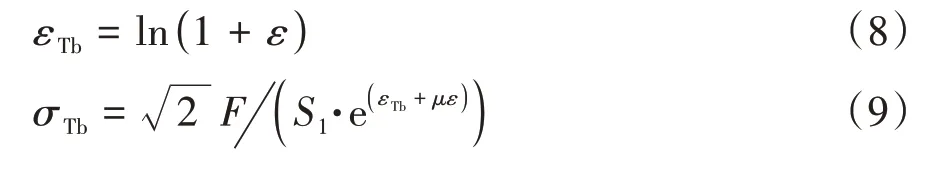
式中：为双向拉伸真实应变；为双向拉伸真实应力；为试件中心测量区域对角方向横截面积；为泊松比。

对单向拉伸、单向压缩、剪切和双向拉伸的真实应力-塑性应变曲线分段进行指数、高次和插值拟合，得到平滑后的曲线，取曲线直线弹性段求解斜率得到弹性模量，屈服点选为应力数值与弹性直线段应力数值相差大约5%的位置，保留拉伸极限之前的数据，之后对曲线进行外延处理，依照曲线延展趋势将曲线外延至塑性应变为1的位置。得到如图6和图7所示的不同应力状态下的真实应力-应变曲线，上述曲线可用于LS-DYNA#MAT_SAMP-1材料模型进行仿真计算。

图7 不同应力状态应力-应变曲线

从图6可知，拉伸试验应变率从1.0×10增加到4.0×10s时，材料的屈服应力从65.5增加到137.4 MPa，增加了109.7%，表明该材料应变率效应明显。

图6 单向拉伸应力-应变曲线

2.2 材料失效参数获取

基于LS-DYNA平台，将材料表征试验获得的数据和曲线代入到仿真模型中，并进行动态拉伸（20、100、400 s）、动态压缩（50 s）、动态剪切（50 s）的有限元仿真对标，仿真模型如图8所示。然后对输入参数进行优化，用于建立MAT_SAMP-1断裂失效材料仿真模型。断裂失效卡片开发总体分为两个部分，第一部分为断裂失效应变参数标定，主要包括断裂失效随应变率和应力三轴度的变化关系；第二部分为断裂尺寸效应参数标定，获取断裂失效与网格尺寸的关系。

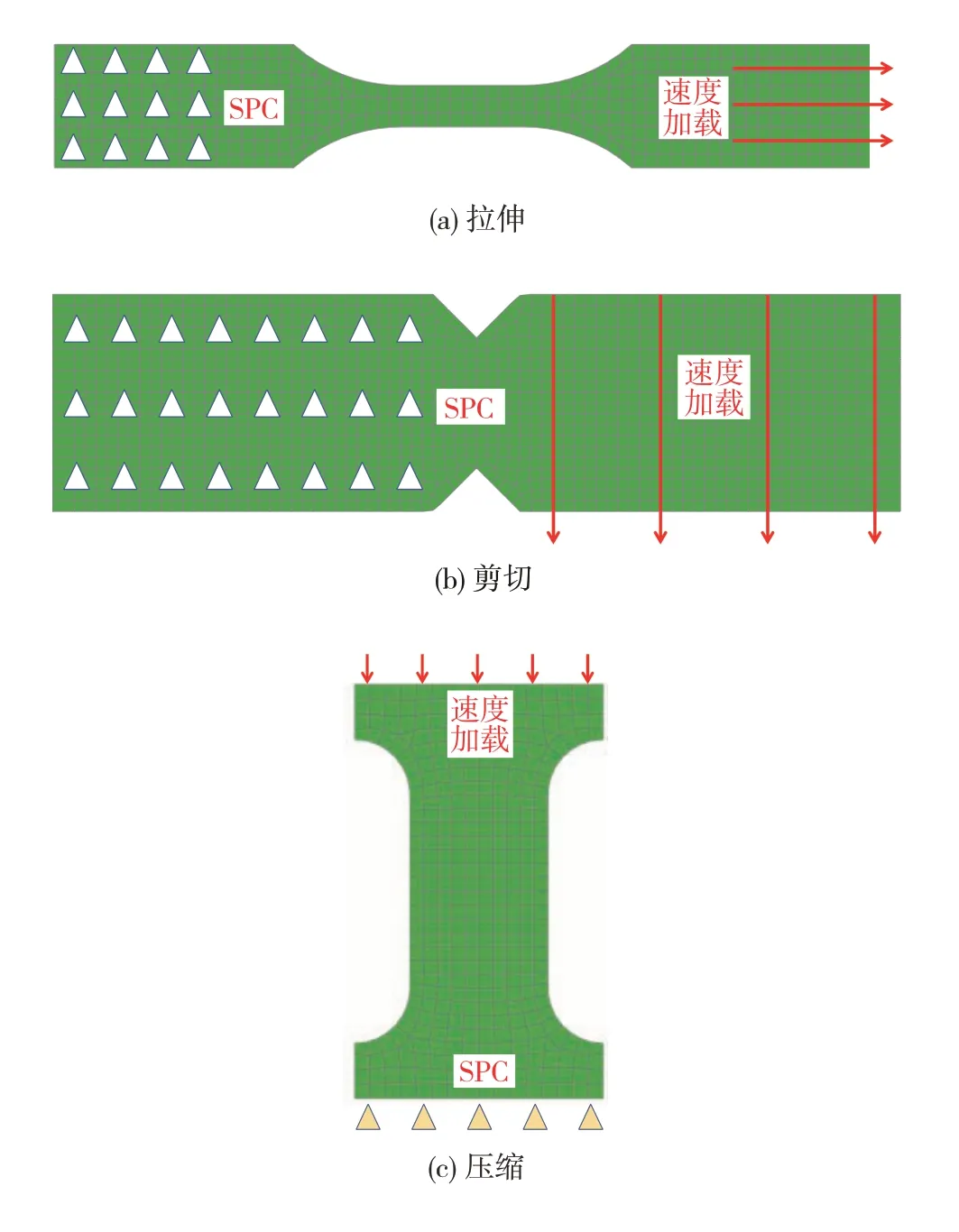
图8 有限元仿真模型

等效塑性断裂应变-拉伸应变率曲线如图9所示，该曲线以单向拉伸各应变率试验曲线的平均等效塑性断裂应变值作为基础输入，并结合静态单向拉伸试验（0.001 s）和高应变率单向拉伸试验（20、100、400 s）进行仿真对标，对输入参数进行优化，获取不同应变率下等效塑性断裂应变值。

图9 断裂应变-应变率曲线

等效断裂塑性应变乘数-应力三轴度如图10所示。分别计算剪切、双向拉伸和压缩试验下得到的等效断裂塑性应变与单向拉伸状态下等效断裂塑性应变的比值（称为等效断裂塑性应变乘数），作为基础输入参数，并结合单向压缩、简单剪切和穿孔工况下的仿真对标对输入参数进行优化。

图10 断裂应变乘数-应力三轴度曲线

在数值仿真计算中，单元网格尺寸的差异会导致分析结果的不同，因为随着网格尺寸的增大，断裂失效发生的时刻会推迟，这主要由于不同网格尺寸的单元在积分点处求解的应力应变存在差异，故MAT_SAMP-1模型加入了断裂尺寸效应标定曲线。基于行人保护碰撞分析模型常用网格尺寸，进行如图11所示的名义网格尺寸为1、2和5 mm穿孔平板的冲压仿真模型对标，以提取不同网格尺寸下的等效塑性断裂应变，得到断裂尺寸效应标定曲线，如图12所示。鉴于断裂应变实际发生正对着冲头的平板中部，横轴以该处壳单元对角线长度表示，而纵轴则以3种网格尺寸中最大断裂应变（对应于图11（a））为基准的比值表示，称之为相对断裂应变。为保证计算稳定，宜适当延长标定曲线，虽然从3个数据点的变化趋势看，随着网格尺寸进一步增大，断裂应变会继续下降，但考虑取大于5 mm网格的几率不大，就简单地将其水平外推至壳单元对角线长度为10 mm的位置。

图11 不同网格尺寸穿孔平板冲压仿真模型

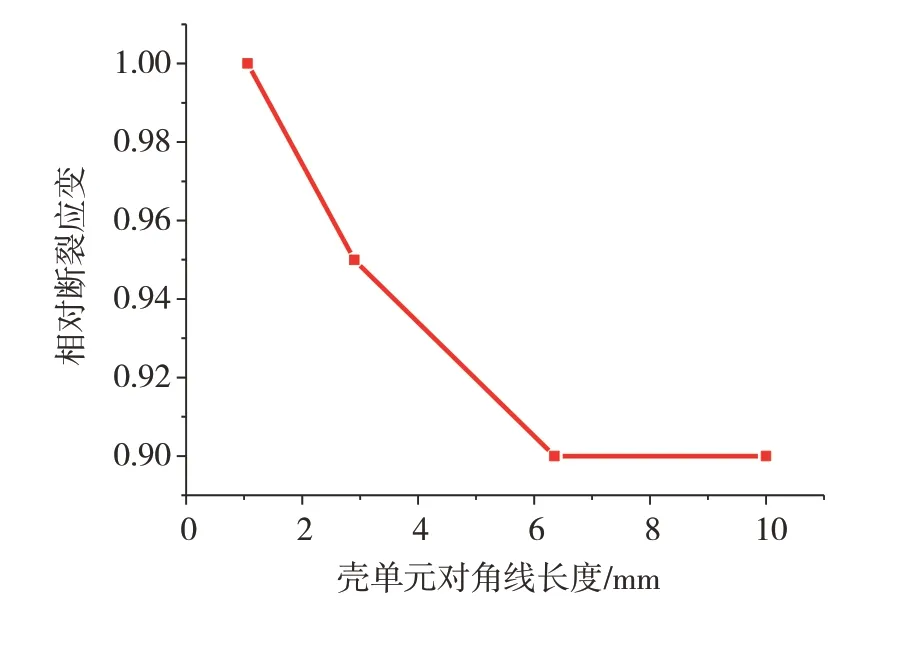
图12 断裂尺寸效应标定曲线

MAT_SAMP-1本构模型主要包括弹性变形参数、塑性变形参数和断裂失效参数，详细参数如表2所示。其中弹性模量和泊松比通过单向拉伸试验参数计算获得。塑性变形参数由2.1节中的材料表征试验获得，断裂失效参数结合试验和仿真对标确定。

表2 MAT_SAMP-1本构模型主要参数

将基于MAT_SAMP-1本构模型建立的PPGF30失效材料模型用于动态拉伸仿真模型进行对标分析。表3为采用ISO527—1—2012标准所述的统计方法，分别统计各拉伸应变率下仿真与试验中屈服至抗拉段的工程应力应变数值，分别计算各应变率下每项指标的仿真试验误差。由表3可知，3种应变率动态拉伸仿真结果在屈服至抗拉段工程应力应变与试验一致性较好，数值综合对标精度在95%以上。图13为动态拉伸仿真与试验断裂图片对比。由图13可见，仿真与试验在不同的拉伸应变率下，试样的断裂形式和断裂位置基本一致。图14为不同应变率下，动态拉伸仿真与试验的应力-应变曲线对比。由图14可见，仿真与试验在不同应变率下的曲线相关度较高。以上结果表明，本文所建立的MAT_SAMP-1#PP-GF30失效材料模型具有较高的仿真精度。

图13 动态拉伸仿真与试验断裂图片对比

图14 单向拉伸仿真与试验曲线对比

表3 单向拉伸仿真与试验误差统计

3 子系统试验与仿真

为验证MAT_SAMP-1#PP-GF30材料模型的准确性，参考行人保护碰撞分析工况，设计了如图15左边所示的大灯子系统验证试验。试验采用落锤冲击，锤头质量57.5 kg，冲击速度3.3 m/s，进行3次重复试验。

建立汽车大灯子系统验证的有限元仿真模型如图15右边所示。大灯各部件采用壳单元建模，基本尺寸5 mm，采用SPC对大灯安装夹具进行约束，采用VELOCITY_RIGID_BODY对锤头模型进行速度加载，采用AUTOMATIC_SURFACE_TO_SURFACE对车灯和锤头进行接触设置，通过“RBDOUT”、“RCFORC”分别读取位移-时间曲线和载荷-时间曲线，由二者生成锤头载荷-位移曲线。

图15 大灯子系统冲击试验与仿真

子系统冲击试验与仿真对比结果如图16~图18所示。从图中可知，采用MAT_SAMP-1#PP-GF30材料模型，大灯子系统仿真模型中大灯支架的断裂位置和失效形式与试验接近。通过试验与仿真，获取的试验与仿真冲击锤头的载荷-位移曲线如图19所示。由图可知，仿真与试验的载荷-位移曲线吻合较好。表4为子系统试验与仿真结果对比。由表4可知，汽车大灯子系统冲击试验的第一峰值载荷和压缩位移的仿真与试验误差分别为3.68%和1.78%，两者误差都小于5%。综合大灯仿真与试验的断裂失效形式及数值误差，表明本文所开发的大灯灯壳断裂失效模型具有较高的仿真精度。

图16 大灯支架1试验与仿真失效对比

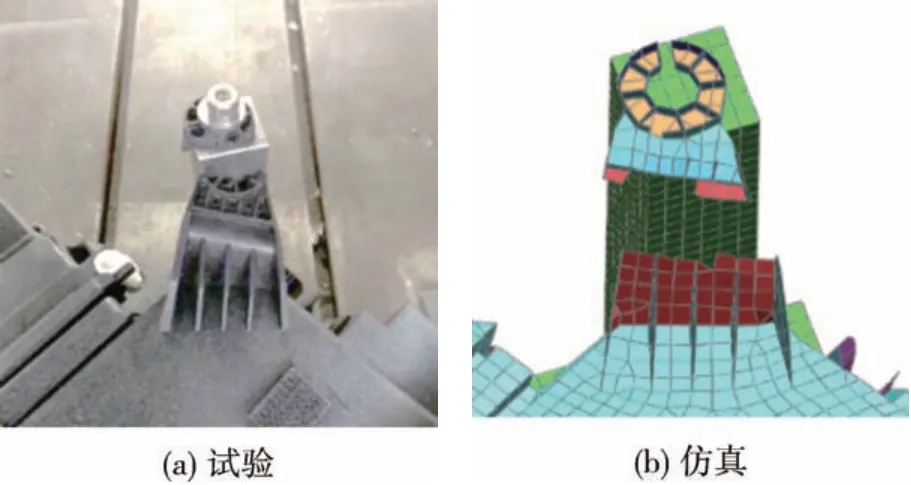
图17 大灯支架2试验与仿真失效对比

图18 大灯支架3试验与仿真失效对比

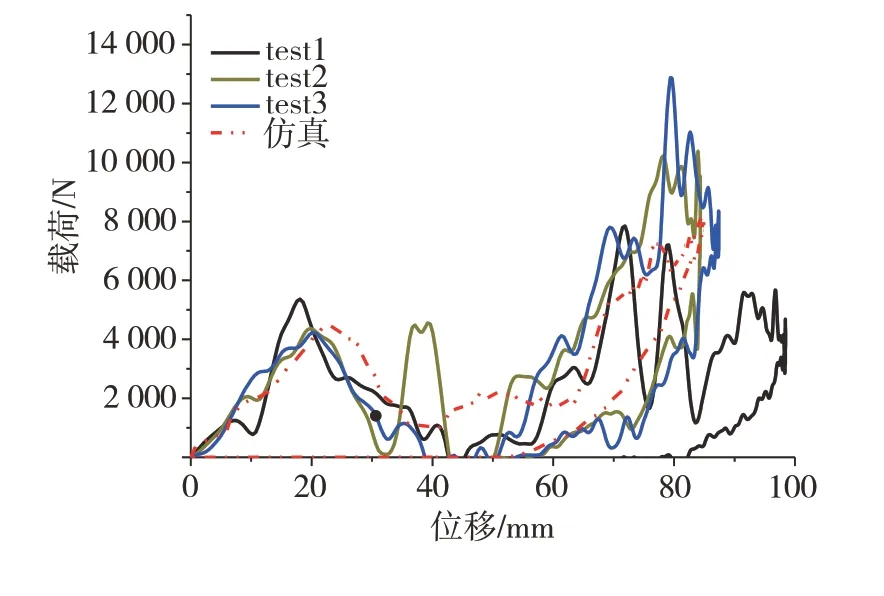
图19 试验与仿真载荷-位移曲线对比

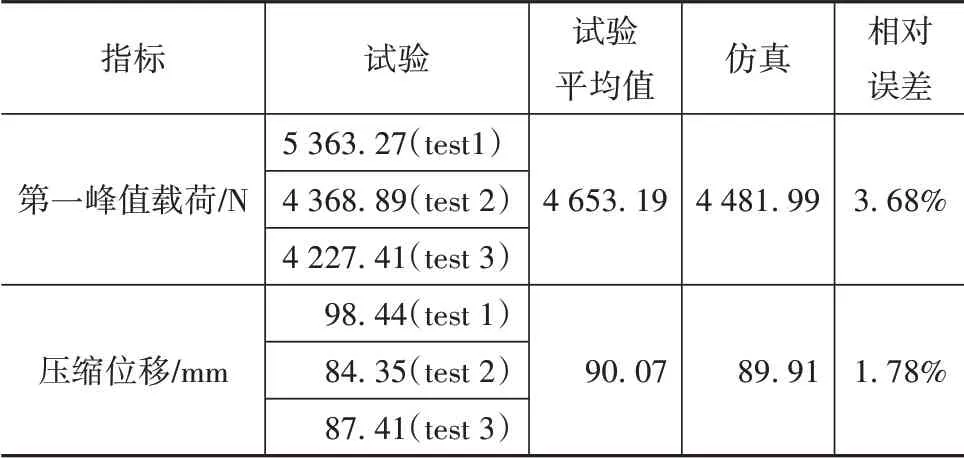
表4 子系统试验与仿真结果对比

4 整车行人腿型碰撞试验与仿真

2021版C-NCAP新车安全评价规程将行人保护的腿型评价冲击器由原来的柔性Flex-PLI升级为aPLI（advanced pedestrian leg impactor）腿型冲击器，该冲击器增加了人体髋部上体模块，比Flex-PLI腿型具有更好的生物仿真性。新的评价规程将行人大腿受到的弯矩损伤纳入评价体系，腿型的开发难度进一步提升，为准确评估所开发车型对行人腿部碰撞的保护性能，要求仿真模型具有较高的仿真精度及汽车大灯的材料准确性，对车灯区域的腿部碰撞保护性能评估具有较大影响。

为验证本文开发的大灯材料模型的准确性，开展了如图20所示的整车行人保护腿部碰撞仿真和试验，仿真采用aPLI腿型，按照2021版C-NCAP测试规程要求以40 km/h的速度冲击车辆前大灯区域。图21为aPLI腿型与该车辆前端结构的冲击位置。由图21可知，大腿弯矩M位置刚好与大灯正面冲击，受大灯影响较大。由于前大灯刚度较大，当大灯冲击到腿型时，腿型上体模块会发生翻转，该翻转对膝部韧带伸长量影响较大，故本文选取大腿弯矩M和两个受车灯影响最大的腿部碰撞损伤评价指标进行研究。

图20 整车腿部碰撞试验与仿真

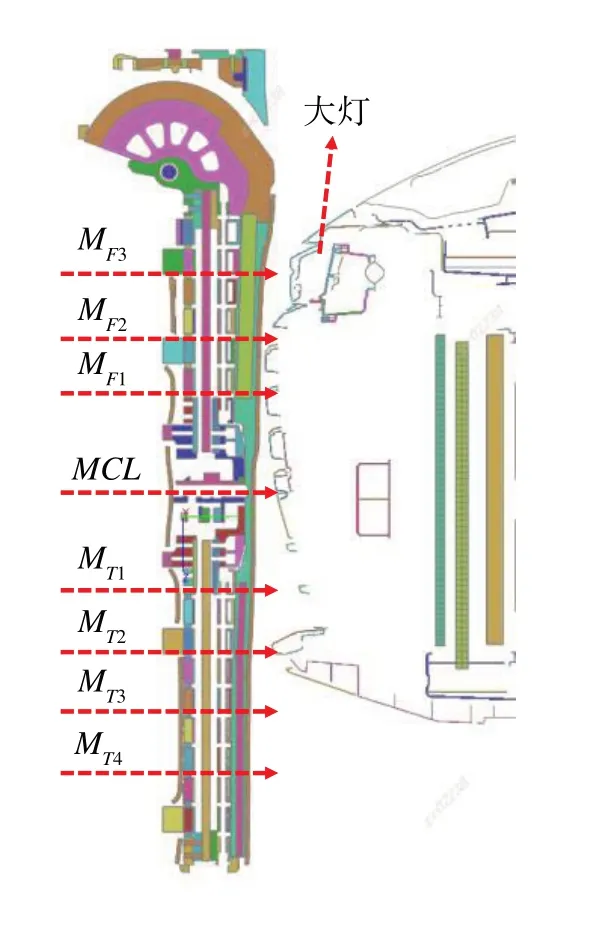
图21 某车型aPLI腿型评价指标位置图

为对比基于MAT_SAMP-1本构建立的PP-GF30失效材料模型的准确性，开展了两种不同本构材料模型的对比分析。case1方案采用本文建立的MAT_SAMP-1#PP-GF30材料模型。case2方案采用基于MAT_PIECEWISE_LINEAR_PLASTICITY本构模型建立的材料模型，该材料模型塑性变形参数主要包括不同应变率下拉伸曲线，未考虑不同应力状态对材料性能的影响，case2方案仿真中未准确预测大灯支架的断裂失效。图22为试验与仿真曲线对比。由图可知，case1方案的M和仿真与试验曲线吻合度更高。表5为整车腿部碰撞试验与仿真结果对比。由表5可知，case1方案的M和仿真与试验误差只有1.93%和2.12%，远小于case2方案的误差。图23为大灯支架试验与仿真失效形式对比。由图23可见，case1方案仿真中大灯支架1和大灯支架2断裂失效形式与试验基本一致。上述研究结果表明，本文基于MAT_SAMP-1本构模型开发的PP-GF30失效材料模型可以有效预测大灯灯壳在行人腿型碰撞工况下的断裂行为，有利于在整车开发中通过模拟手段来准确分析某车型对行人的碰撞保护性能。

图22 试验与仿真曲线对比

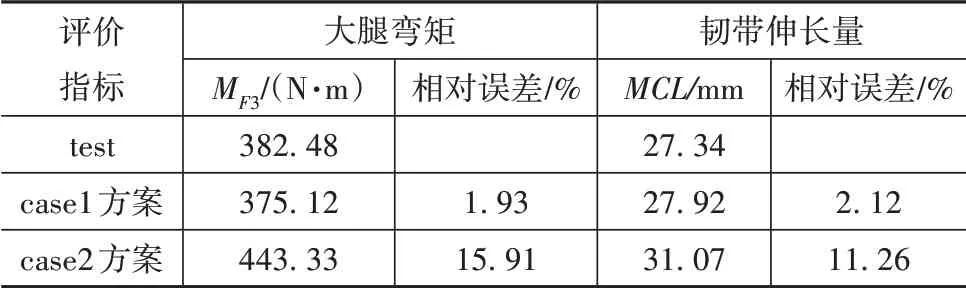
表5 整车腿部碰撞试验与仿真结果对比

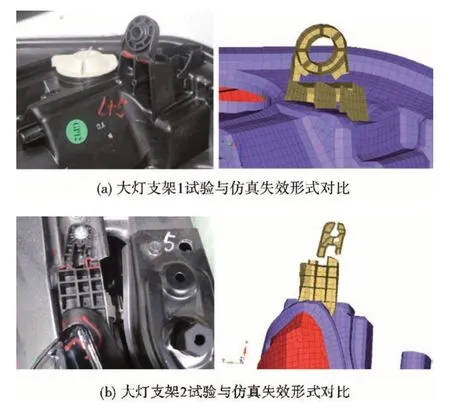
图23 大灯支架试验与仿真失效形式对比

5 结论

为准确预测整车行人保护碰撞工况中汽车大灯的断裂失效行为，通过对汽车大灯灯壳PP-GF30进行材料级、子系统和整车级的试验与仿真对标研究，建立了其断裂失效模型，结果表明：

（1）PP-GF30材料在动态拉伸下应变率效应明显，准静态与动态拉伸下的应力-应变曲线差异较大。大灯的碰撞冲击仿真中，须考虑不同应变率的影响，使材料能真实反映大灯在碰撞工况下的力学行为。

（2）PP-GF30材料断裂失效与应力状态和应变率有较大关系，须通过试验与仿真对标获取不同应变率和应力状态下的断裂失效参数，同时断裂失效模拟模型还须考虑网格尺寸效应的影响。

（3）基于MAT_SAMP-1本构建立的断裂失效模型可以准确预测PP-GF30材料在汽车-行人碰撞的冲击工况下的断裂失效行为。

本文中所介绍的塑料材料失效模拟方法可推广到其它汽车-行人碰撞工况相关的塑料材料。