剪切模量和密度反射系数近似方程及叠前地震反演

范晓辉,杨景阳,单 博

(中国石油大学(华东)地球科学与技术学院,山东青岛 266580)

地球物理反演的本质是依据地震数据获取我们所需地层的物性、弹性参数,揭示地下地层空间展布和含油气性等特征。OSTRANDER[1]初次提出AVO技术,揭示地震反射波振幅反映储层特征的奥秘,由于Zoeppritz方程[2]精确求解的复杂性,许多学者开展了基于Zoeppritz方程的AVO方法研究。AKI等[3]在《定量地震学》中,对Zoeppritz方程进行了简化近似。拉梅参数(λ,μ)是储层预测和流体识别中最常用的弹性参数,分别表征岩石的压缩性和刚性,相较纵、横波速度和密度参数具有更好的预测及识别能力[4]。GOODWAY等[5]将Fatti近似式改写为模量组合和密度表示的形式,通过提取纵、横波阻抗相对变化量求取纵、横波阻抗信息,进而依据公式计算λρ和μρ,但其本质仍是一种间接反演方法,而间接计算产生的累积误差会降低预测精度[6-7]。XU等[8]提出利用体积模量K和拉梅常数λ,μ表征的完全隐含速度信息的近似方程。在密度相对变化较小时,能够利用两项参数反映入射角不超过45°的反射特性。GRAY等[9]基于Aki-Richards近似方程提出了由体积模量/压缩模量、剪切模量和密度的相对变化率表示的反射系数近似公式,实现利用叠前地震数据直接反演出λ和μ,可以更加准确地识别岩性和流体。CONNOLLY[10]率先提出弹性阻抗的概念,能够获得纵、横波速度和密度信息,进而计算其它弹性参数。王保丽等[11]基于Gray近似方程,推导了由λ、μ和ρ三参数表达式表示的弹性阻抗方程,并进行标准化处理,可以直接从弹性阻抗数据中提取拉梅参数。宗兆云等[12]基于平面波入射假设条件,推导了基于杨氏模量Y、泊松比σ和密度D的YPD反射系数近似方程,实现目标参数的直接反演,能够有效识别页岩气“甜点”。

URSIN等[13]认为利用直接从常规纵波地震数据反演纵、横波速度和密度3个参数难度较大。张春涛等[14]认为利用纵波地震数据一般很难反演得到密度比。叠前AVO反演能够利用更多地下真实数据,其本质仍是不适定问题,一般通过删除第三项提高反演问题的稳定性[15]。SMITH等[16]利用Gardner经验关系式[17]改写Aki-Richards近似方程,消除密度项,虽然稳定性有所提高,但经验关系式与实际地层的吻合情况严重影响反演的精确度。

在Zoeppritz方程的基础上,提出一种关于剪切模量和密度的AVO直接反演方法,该方法直接提取剪切模量和密度,避免间接计算引起的误差。本方法仅涉及两参数反演,且未引入经验关系式,具有比常规三参数反演更好的稳定性。通过模型数据试算与方法对比,验证了此方法正、反演问题的有效性与稳定性。最后,将其应用于实际叠前地震数据,以验证方法在岩性识别与储层预测中的正确性。

1 方法原理

1.1 AVO正演公式

ZOEPPRITZ[2]基于平面波理论,根据斯奈尔(Snell)定理、界面两侧位移和应力的连续性,建立了用位移振幅比表示的反射透射系数,对Zoeppritz方程组进行简化推导:

(1)

式中:RPP、TPP、RPS、TPS分别为纵波反射系数、纵波透射系数、转换横波反射系数和转换横波透射系数;vP1、vP2、vS1、vS2分别为界面两侧的纵、横波速度;α1、β1、α2、β2分别为界面两侧的纵、横波的反射和透射角;ρ1、ρ2分别为界面上、下地层的密度。(1)式左右两侧矩阵中的速度、角度项均满足Snell定律。则有:

(2)

式中:P为射线参数。记x=sinα1,a=vP2/vP1,b=vS2/vS1,c=ρ2/ρ1,γ1=vS1/vP1,代入(1)式整理可得:

(3)

简化矩阵形式为:

(4)

主要对纵波反射系数进行重新推导,根据克莱姆法可知:

(5)

det表示求取矩阵的行列式,其中:

(6)

式中:A11是将A中的第一列用B替代所得到的矩阵。借鉴AVO公式常用各类参数相对变化率表示反射系数的方式,引入横波、密度的相对变化率,记RS=(vS2-vS1)/(vS2+vS1),Rρ=(ρ2-ρ1)/(ρ2+ρ1),可对(3)式中参数进行转换:

(7)

对(7)式泰勒展开可得:

(8)

式中:Rμ=(μ2-μ1)/(μ2+μ1),表示界面上、下剪切模量的相对变化率;T=γ1/γ2,表示界面上、下地层横、纵波速度比的比值,可通过测井曲线获得。

同样展开角度项,则有:

(9)

将(8)式、(9)式代入(5)式,为保持精度,角度项保留至4次方项,整理可得:

(10)

其中,

A1=B1=T+1

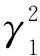
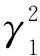
(10)式为由剪切模量、密度的相对变化率表示的反射系数方程,记为μ-ρ方程,对其进行化简得:

RPP(θ)=ARμ+BRρ+C

(11)

其中,

假定叠前地震数据有m个入射角,每一道地震数据有n个时间采样点,结合褶积模型,反射系数与子波褶积得到合成地震记录,即正演方程为:

(12)

式中:d(θ)为合成地震数据;W(θ)为子波矩阵;RPP(θ)为PP波反射系数;上标均代表对应时间采样点;下标均代表对应入射角。

1.2 与Aki-Richards近似方程的比较

AKI等[3]在《定量地震学》中给出了Zoeppritz方程的经典近似式为:

(13)

由于vP=vS/γ,结合纵波速度与剪切模量的关系,得:

(14)

将(14)式代入(13)式,Aki-Richards近似方程可改写为:

(15)

其中,

(16)

对(16)式两端取正弦得:

(17)

对(17)式右端余弦项泰勒展开

(18)

(19)

将(18)式和(19)式代入(17)式且忽略高阶项,则有:

(20)

将(8)式代入(20)式

(21)

(22)

将(21)式和(22)式代入(15)式,保留相对变化率的一阶近似,有:

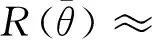
(23)

其中,

考虑Aki-Richards近似方程成立的假设条件为相邻两层介质的弹性参数变化较小,则

(24)

(23)式可表示为:

(25)

比较(10)式和(25)式可以发现,假设相邻两层介质的弹性参数变化较小,Aki-Richards近似方程在外推过程中,γ的平均值用界面上层的γ替代,从而得到Aki-Richards近似方程等价于μ-ρ方程,但μ-ρ方程在推导过程中没有进行平均值的近似,避免了这部分近似的误差。

2 正演模拟

为测试μ-ρ方程的可行性,基于CASTAGNA等[18]提出的AVO分类方法建立了4类AVO模型(表1至表4),且都利用Zoeppritz方程和μ-ρ方程(图例以“μ-ρ”表示)、Aki-Richards近似方程和Gray近似方程计算4种模型界面的纵波反射系数并计算各类方法与精确值之间的误差(图1至图4)。图1a、图2a、图3a和图4a分别是第Ⅰ、Ⅱ、Ⅲ、Ⅳ类AVO模型的正演结果;图1b、图2b、图3b和图4b分别是三类近似方法求得的第Ⅰ、Ⅱ、Ⅲ、Ⅳ类AVO模型的反射系数与Zoeppritz方程求得的准确值之间的误差(已校正法向入射时初始误差)。对比3种方法的正演结果可以看出,在0入射时,μ-ρ方程与Gray近似方程的正演结果均与准确值存在不同程度的误差,说明在法向入射时两种方法均存在直接引入弹性参数的转化误差。但就整体趋势而言,μ-ρ方程正演结果在4类模型中均与实际模型趋势吻合最好,误差图更加直观地表明,误差基本来自法向入射时计算误差,在校正初始误差后,本文提出的方法明显比其它两种方法更为精确。此外,Aki-Richards近似方程和Gray近似方程在4类模型中的正演结果具有相同的趋势,且随着入射角度的增加两者逐步偏离精确Zoeppritz方程计算结果,其根本原因是Gray近似是基于Aki-Richards方程参数转换所得,本质上基于一种近似的不同表示,两种方法涉及的角度项仅保留至二阶,在大角度入射时易产生较大误差,新方法的角度项保留至四阶,能够较好地避免此类误差。

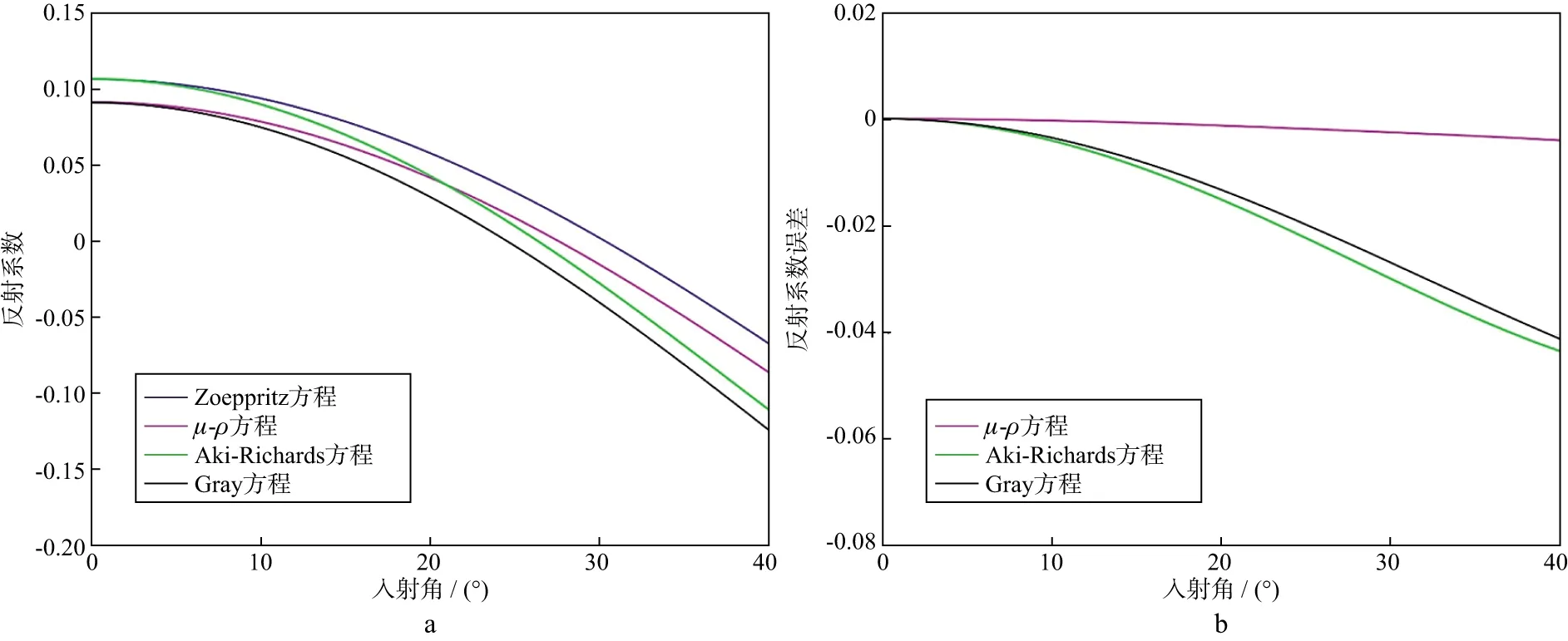
图1 第Ⅰ类AVO模型不同方程计算的反射系数(a)和反射系数误差(b)对比

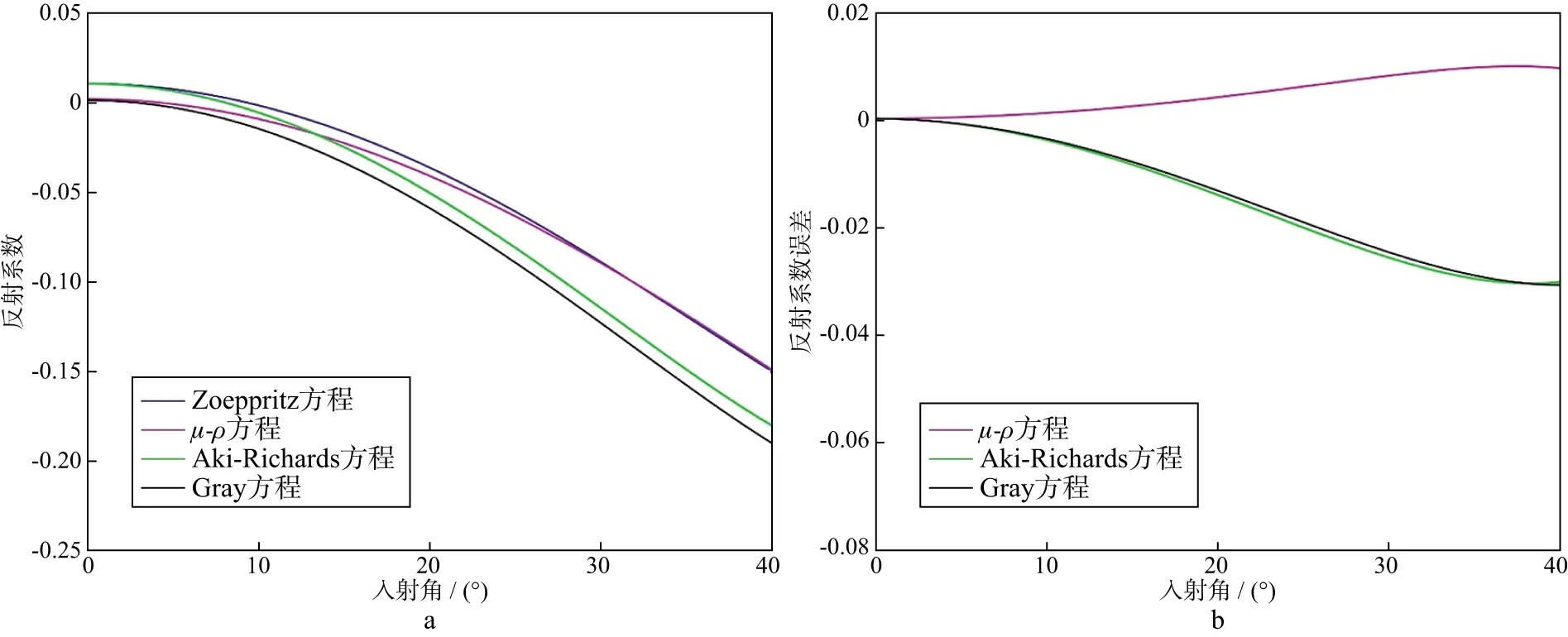
图2 第Ⅱ类AVO模型不同方程计算的反射系数(a)和反射系数误差(b)对比

图3 第Ⅲ类AVO模型不同方程计算的反射系数(a)和反射系数误差(b)对比

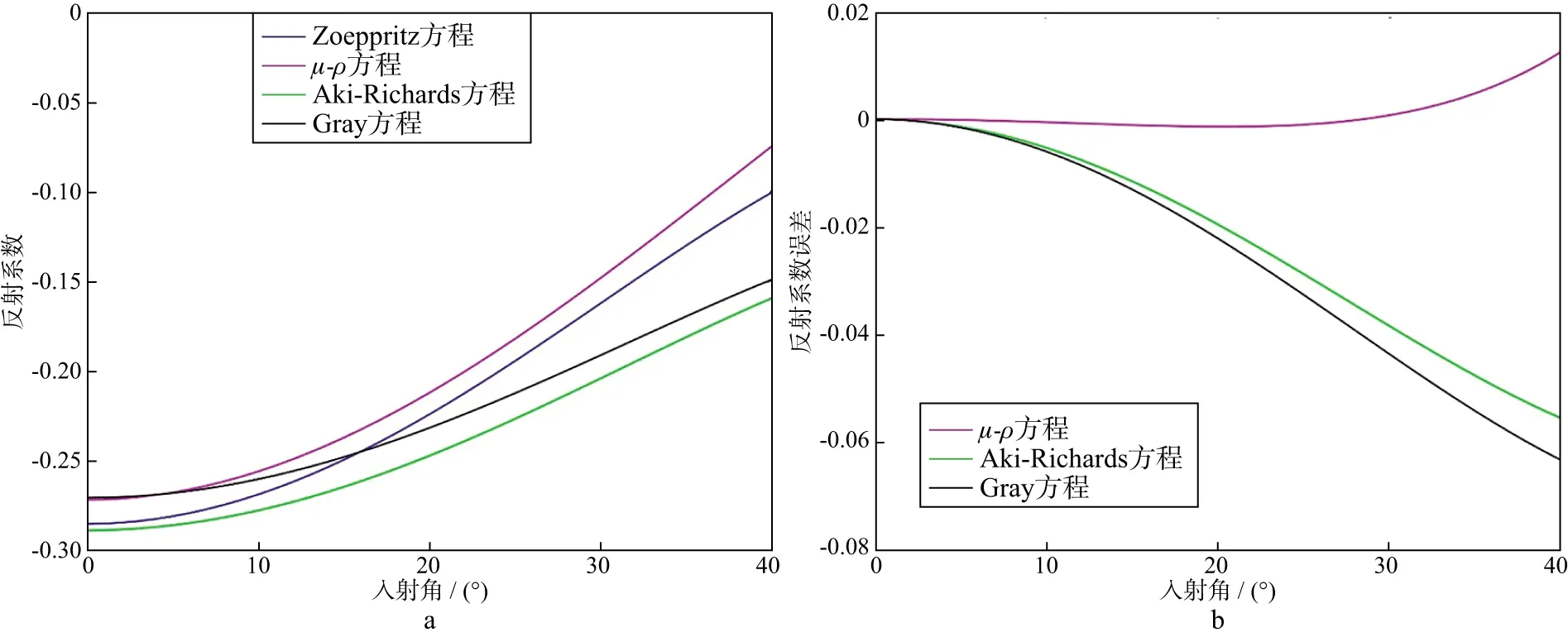
图4 第Ⅳ类AVO模型不同方程计算的反射系数(a)和反射系数误差(b)对比

为验证μ-ρ方程的稳定性,对建立的4类AVO模型(表1至表4)进行条件数分析。图5为4类AVO模型采用3种方法正演时,条件数随最大入射角度的变化情况,其中最小入射角度保持为0,最大入射角度范围为5°～40°。由图5可以看出,当最大入射角度比较小时,3种方法的条件数都较大,表明过小角度入射时反演问题非常不稳定,因此需要获取较大的偏移量信息以提高反演的稳定性。同时可以看出,μ-ρ方程所得条件数比以往3项参数的近似方程条件数成指数级降低,表明μ-ρ方程的稳定性远高于Aki-Richards近似方程和Gray近似方程。

表1 第Ⅰ类AVO模型参数

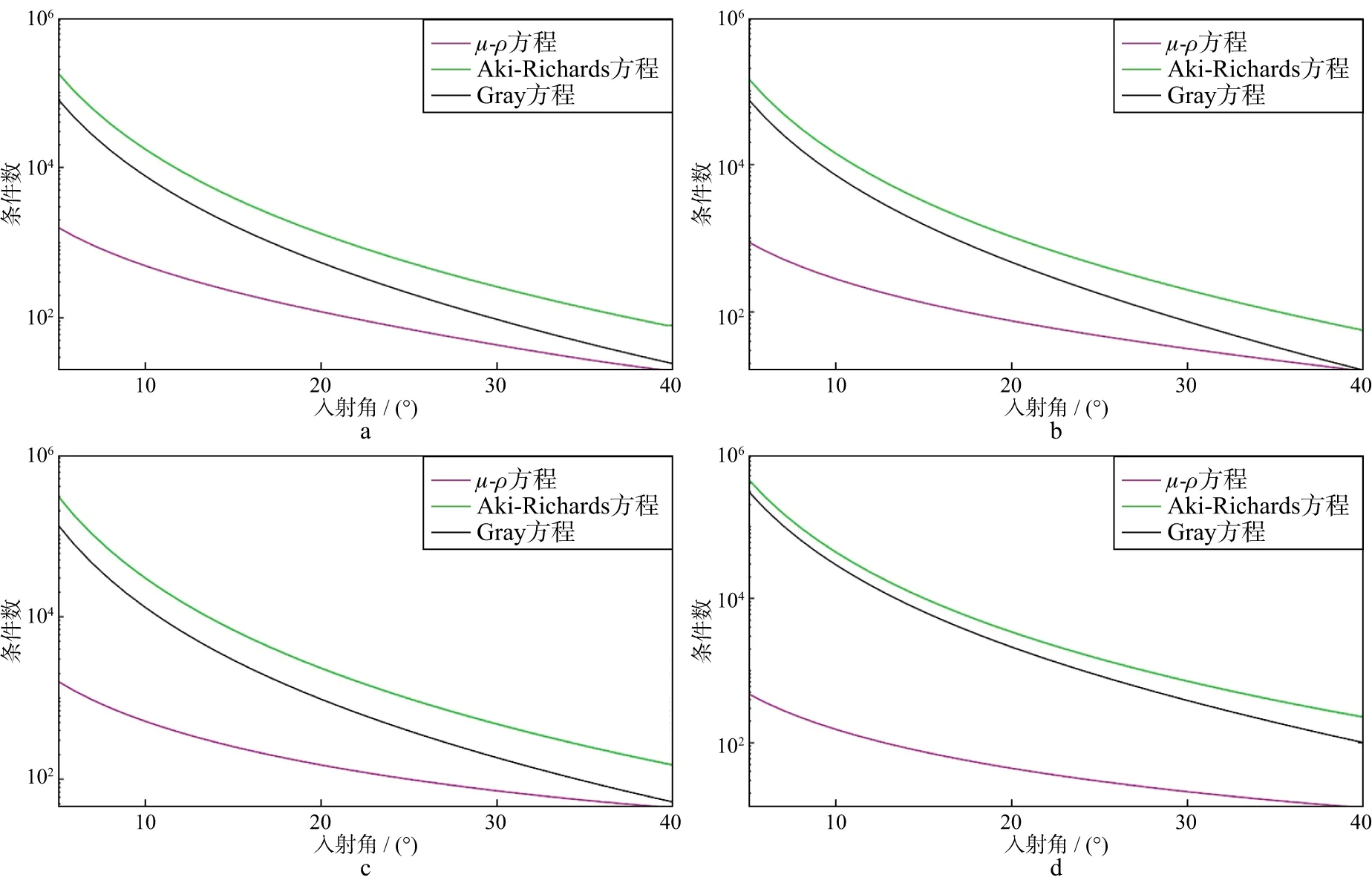
图5 4类AVO模型条件数a 第Ⅰ类AVO模型; b 第Ⅱ类AVO模型; c 第Ⅲ类AVO模型; d 第Ⅳ类AVO模型

表2 第Ⅱ类AVO模型参数

表3 第Ⅲ类AVO模型参数

表4 第Ⅳ类AVO模型参数

3 反演分析

3.1 一维层状模型模拟

为验证μ-ρ方程反演的可行性,构建一维五层模型进行反演模拟。反演算法基于最小二乘法,模型数据如表5所示。利用Zoeppritz方程获得模型精确数据,分别利用μ-ρ方程、Aki-Richards近似方程和Gray近似方程对精确数据进行μ、ρ反演并求取各方法计算结果与精确值之间的误差,结果如图6和图7所示。对比3种方法的反演结果,两种三参数近似方程在881～1040m层段与真实数据拟合相对较好。当深度较大时,反演误差增大,认为是反演迭代中误差累积所致。对比3种方法的结果认为,μ-ρ方程直接反演得到的μ、ρ与真实模型的拟合误差最小,原因在于此方法直接提取弹性参数,减少了累积误差且两参数反演具有更高的稳定性。Aki-Richards近似方程和Gray近似方程在层状模型反演时仍具有相同的趋势,再次验证两种近似式本质上是基于一种近似的不同表示。

图6 一维层状模型μ的反演结果(a)及误差(b)

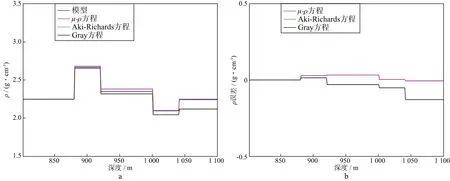
图7 一维层状模型ρ的反演结果(a)及误差(b)

表5 一维层状模型参数

假设井数据丰富,可以通过井位速度信息求取泊松比,结合μ-ρ方程直接反演得到μ,可以通过拉梅参数与泊松比的关系获得λ。在本次模型模拟中代入每层真实泊松比,按上述方法计算λ,并利用Gray近似方程对精确数据进行直接反演得到λ,结果如图8 所示。由图8可以看出,此方法求解出的λ与真实数据吻合程度更高,表明在井数据丰富条件下,μ-ρ方程能准确获得λ。

图8 一维层状模型λ的计算结果(a)及误差(b)

3.2 反演流程

在实际地震反演中,通常采用离散方程进行计算,正演公式(12)可直接简写为矩阵形式:

d=Wr

(26)

式中:d为叠前地震数据,W为子波矩阵,r为反射系数矩阵,即(11)式。

基于最小二乘原则约束反演误差,考虑L0范数约束下的反演问题直接求解是NP-hard[19],采用L1范数构建稀疏脉冲反演的目标函数为:

(27)

式中:‖·‖2表示测量反演误差的L2范数,‖·‖1表示反射系数的L1范数,用于测量反射系数序列的稀疏性;l1是L1范数的正则化因子。

公式(27)中,L1范数测量了反射系数序列的垂向稀疏性,并没有考虑多道反射系数序列的横向变化和连续性,因此引入核模约束[20],以约束r为低秩,保证r相邻道具有相关性,其定义为矩阵r所有奇异值的和,即

(28)

式中:σ(i)为矩阵r的第i个奇异值,则(27)式可以改写为:

(29)

式中:l2为核模约束的正则化参数。在实际数据处理中,仅通过L1范数的稀疏约束和核模约束并不能完全准确地恢复低频分量。因此,将模型参数的先验信息rpriori作为正则化约束项加入到目标函数中,目标函数(29)可写为

(30)

式中:l3为先验模型的正则化约束系数。(30)式即为最终的叠前反演目标函数。可以通过迭代重加权最小二乘算法[21]进行求解。

3.3 应用实例

为验证μ-ρ方程在实际资料反演中的可行性,选取某工区的实际地震数据进行测试。该工区的叠前地震数据包括3个不同角度范围的部分角度叠加数据体,叠加剖面如图9所示,其中,图9a为0°～10°叠加剖面,图9b为8°～17°叠加剖面,图9c为15°～25°叠加剖面。首先,对工区内的测井资料进行预处理。然后,利用求解基于μ-ρ方程的反演目标函数实现剪切模量和密度参数的反演,反演结果如图10和图11所示。图10为剪切模量μ的反演剖面与井位反演曲线。图10a中红色曲线为井的位数据经滤波后计算的μ曲线;左侧为井的岩性图。由图10可以看出,反演剖面的高μ区与井的砂岩段吻合较好,说明通过反演μ可以较好地识别岩性。图10b为井位位置的反演结果。其中红色曲线为μ-ρ方程反演结果,证实基于μ-ρ方程的反演结果与测井曲线吻合较好。图11为密度ρ的反演剖面与井位反演曲线,井位反演结果与测井曲线基本一致。图10和图11表明,基于μ-ρ方程得到的反演剖面与测井解释结果基本吻合,能得到较为精确的μ和ρ值,将其与其它参数联合分析、构建流体因子,可更精确地识别岩性和流体。

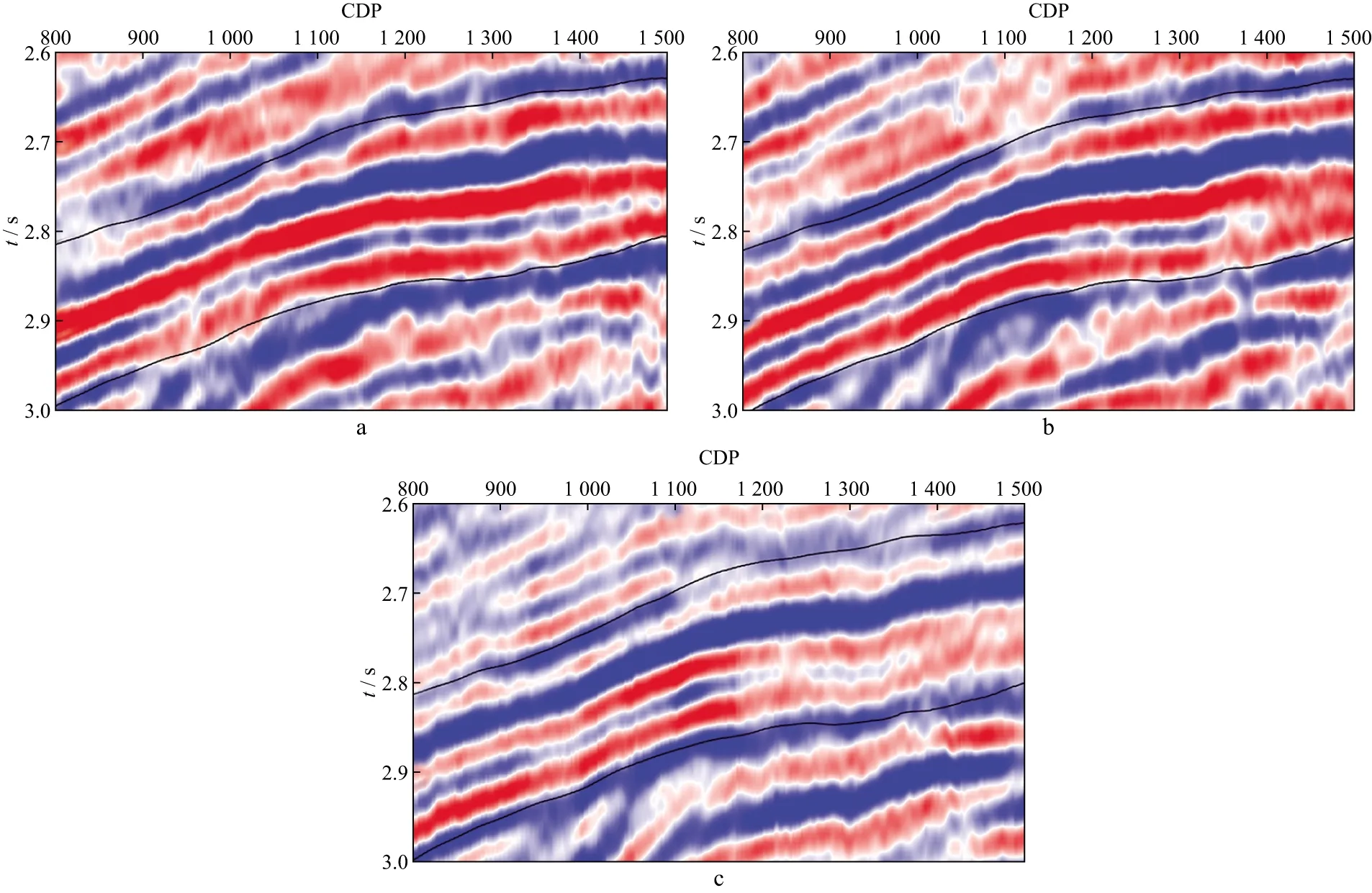
图9 部分角度叠加剖面a 0°～10°叠加剖面; b 8°～17°叠加剖面; c 15°～25°叠加剖面

图10 剪切模量μ的三维反演剖面(a)及井位反演对比(b)

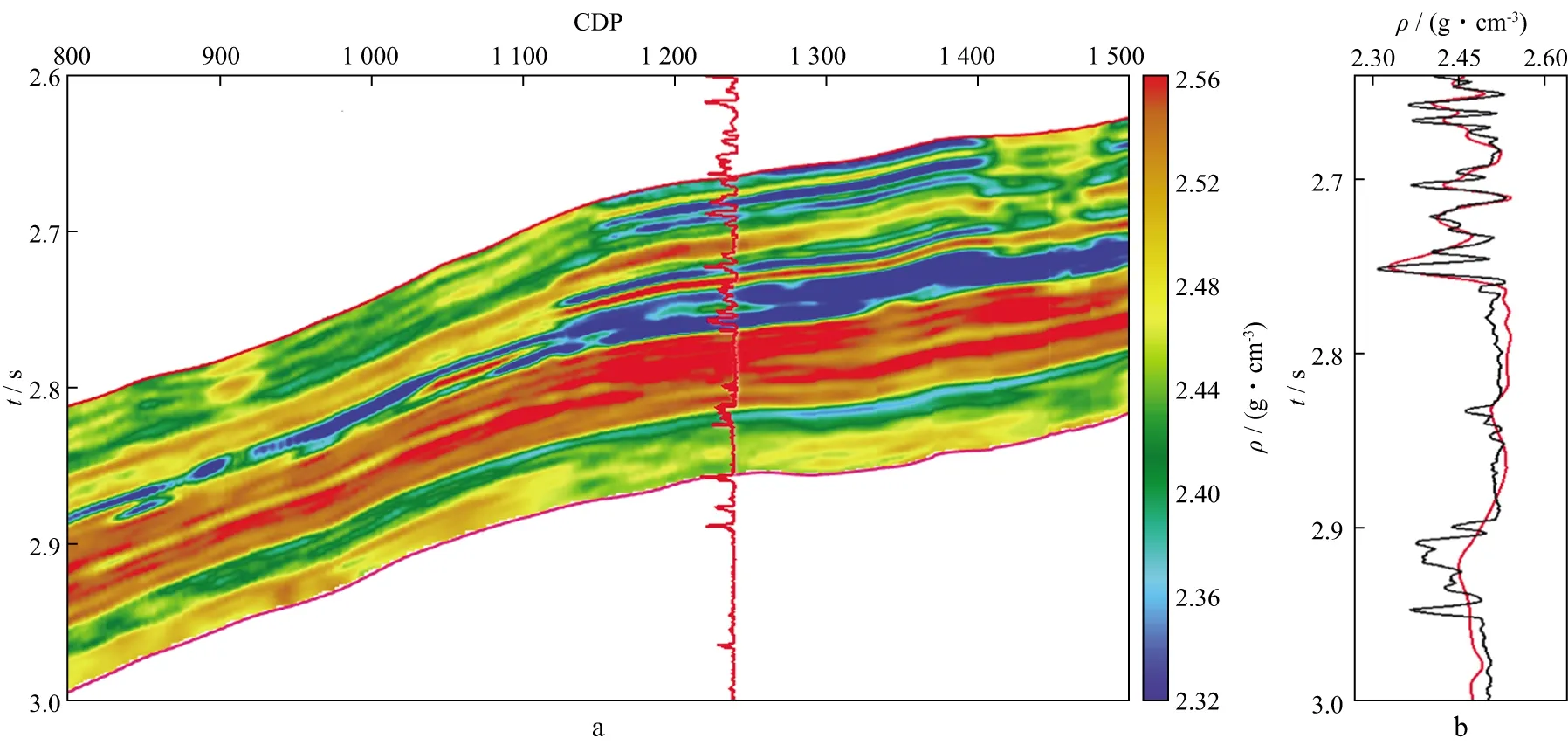
图11 密度ρ的三维反演剖面(a)及井位反演对比(b)

4 结论

拉梅参数是储层预测和流体识别中最常用的弹性参数,目前常用的提取方法是通过反演纵、横波速度间接计算获得,这会导致误差累积。同时,利用叠前地震数据实现三参数的精确反演仍是一个难题。我们提出了一种基于剪切模量和密度的两参数纵波反射系数方程,并将该方程应用于实际资料处理,能够较好地直接反演出剪切模量和密度。正演模拟和反演分析结果表明:

1) 从Zoeppritz方程出发,直接推导由剪切模量和密度相对变化率表征的反射系数方程,未引入经验关系式,且角度项保留至四阶,在较大角度入射时同样具有较好的正演效果。避免了反演出现累积误差。

2)μ-ρ方程涉及两参量,条件数远低于Aki-Richards方程与Gray近似方程,具有更高的稳定性。

3) 在井资料丰富的情况下,基于μ-ρ方程精确反演得到μ,进而结合井位信息以及拉梅参数与泊松比的关系式获得λ,实现三参数的获取。

4) 引入核模约束项以及先验信息约束项构建反演目标函数,能够增强反演的横向连续性并还原原始数据的频率信息,实际资料处理证实本方法能较好地拟合井数据,反演得到较为精确的μ,ρ值,并用于岩性识别。

5) 正演模拟与反演分析结果均表明,μ-ρ方程具有较高的稳定性和准确性,基于μ-ρ方程反演得到的弹性参数可与其它参数联合分析、构建流体因子,可更精确地识别岩性和流体。