高速铁路高低塔斜拉桥抗震性能研究

王 栋

(安徽省皖北城际阜淮铁路股份有限公司,合肥 230601)

引言

大跨径斜拉桥由于其本身结构的力学特性，受地震作用影响不容忽视[1]，因此，有必要对其进行结构抗震性能研究。国内外已有不少学者对斜拉桥抗震性能进行研究，管仲国、李建中[2]针对大跨度的抗震体系发展现状与未来趋势开展研究，系统总结了大跨度桥梁的抗震机理；周亚栋等[3]和曾勇等[4]对于全漂浮体系斜拉桥和单索面斜拉桥进行动力特性分析，为抗震研究提供了参考；李立峰等[5]和黄永福等[6]对几种横向抗震体系进行研究，确定了合理横向抗震结构体系；万乐乐、刘保文、贾毅等[7-9]针对矮塔斜拉桥和大跨度斜拉桥进行非线性时程分析，研究了减隔震装置对于斜拉桥的减震效果；许智强等[10]和潘思璇等[11]进行了行波效应非一致激励的研究，确定了行波效应对斜拉桥响应规律。与其他斜拉桥相比，大跨度高低塔斜拉桥又有其特殊的性质，如两桥塔不对称导致的振型特性、两桥塔的内力变形差异等。

以阜淮高铁跨越颍河高低塔混合梁斜拉桥为例，探讨固定支座设置及阻尼器参数对结构抗震性能的影响，确定合理的桥梁结构形式，依据铁路斜拉桥抗震设防目标，分析该桥的结构抗震性能。

1 桥梁概况

新建阜淮高铁颍河斜拉桥为主跨230 m高低塔双索面混合梁斜拉桥，全长489.5 m(含两侧梁端至支座中心各0.75 m)，主桥采用高低塔非对称边跨布置形式，设置2个辅助墩和2个过渡墩，跨径布置为(31+73+230+114+40) m。桥塔采用H形花瓶塔，由下、中、上塔柱及上横梁、下横梁5部分组成。小里程侧主塔为低塔，塔全高83.4 m，桥面以上部分塔高60.6 m。大里程侧主塔为高塔，塔全高115.1 m，桥面以上部分塔高84.8 m。低塔设置18对斜拉索，高塔设置24对斜拉索，横向双索面布置。主梁位于下横梁上方，由钢-混结合梁、混凝土梁及钢混结合段3部分组成，主梁高为3.8 m。主梁全宽18.6 m(含风嘴)。桥梁位于7度区，地震动峰值加速度为0.1g。

该桥为纵向半漂浮体系，索塔与主梁间设置横向活动支座和横向抗风支座、多向活动支座和横向抗风支座，在高塔设置固定支座，纵向设置黏滞阻尼器；过渡墩与辅助墩设置纵向活动支座及多向活动支座。总体布置如图1所示。

图1 阜淮高铁颍河特大桥斜拉桥总体布置(单位：m)

2 动力有限元分析

2.1 结构有限元模型

针对颍河斜拉桥建立Midas Civil有限元模型，桥塔、桥墩、主梁及桩基采用梁单元模拟，斜拉索采用桁架单元模拟。桥面铺装、栏杆、混凝土板自重及后期压重等作为二期恒载考虑，并将其转化为质量。同时考虑桩土结构的相互作用，采用“m”法计算桩基的桩-土弹簧作用[12-14]，并对桩基施加土弹簧约束。两侧分别建立一联引桥作为主桥一侧的边界条件。全桥共划分为4 596个节点、4 363个单元。计算模型如图2所示。

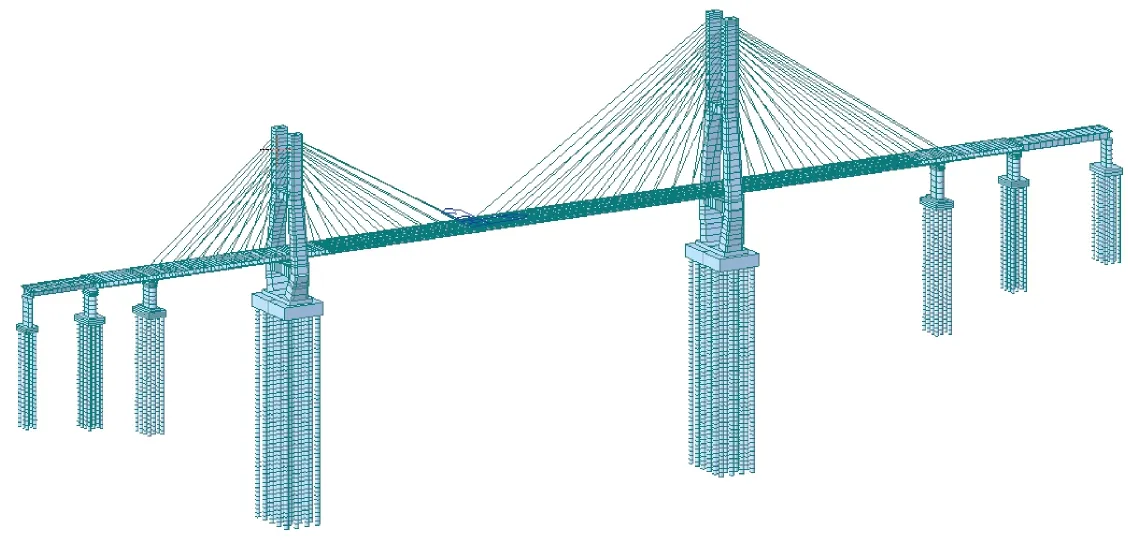
图2 斜拉桥有限元模型

2.2 地震动输入

地震安评报告显示，本地区被判定为 Ⅲ 类建筑场地，设计地震时，采用50年10%的超越概率的对应参数；罕遇地震时，采用50年2%的超越概率的对应参数。工程场地设计地震动参数如表1所示。

表1 工程场地设计地震动参数

地震水平加速度时程选用安评报告提供的7条水平地震加速度时程波，并取7条波的平均响应作为最终输出结果，图3为2条典型地震波曲线。地震输入方式为纵向+竖向和横向+竖向2种方式。

图3 设计地震和罕遇地震波加速度时程曲线

3 结构体系对抗震性能影响分析

斜拉桥的整体抗震性能主要从结构内力与变形两方面进行考虑，均应越小越好[15-16]。然而，在地震作用下，斜拉桥的内力与变形总是相互矛盾，因此，应在其内力与变形之间相互协调，确定其合理的结构设计方案。针对罕遇地震作用对高低塔斜拉桥结构影响，分别对结构约束体系、固定支座位置及阻尼器参数进行分析。

3.1 约束体系影响分析

斜拉桥根据主梁、塔、索和墩的不同组合分为4种结构体系：全漂浮体系、半漂浮体系、塔梁固结体系、刚构体系[17]。其中，半漂浮体系作为斜拉桥一种重要的结构体系形式，其塔墩固结，主梁在塔墩上设置竖向支撑；支座设置可设1个固定支座，3个活动支座，也可设置4个活动支座。针对该桥特点，进行方案设计时考虑了以下4种结构体系。(1)全漂浮体系：塔梁分离、塔梁间设置垂直吊索。(2)仅设竖向支座的半漂浮体系：塔梁分离，塔梁间仅设置竖向支座。(3)设固定支座的半漂浮体系：塔梁分离，高塔采用固定支座，低塔采用活动铰支座。(4)刚构体系：塔梁固结或采用固定支座进行约束。

针对以上不同结构体系进行抗震计算，分析结构在地震作用下的受力及变形情况，综合对比分析，确定最合理的结构体系。主梁、塔顶变形、塔底弯矩、桩基弯矩如图4～图7所示。

图4 4种结构体系主梁位移对比

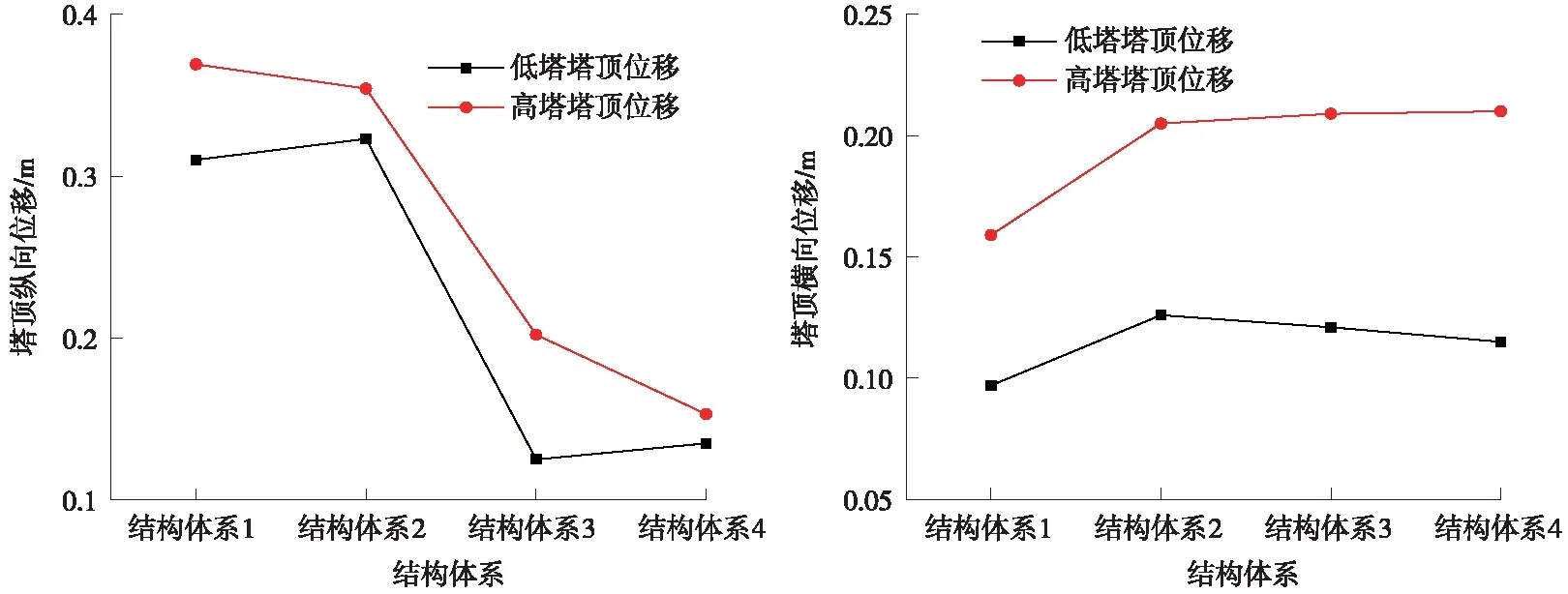
图5 4种结构体系塔顶位移对比

图6 4种结构体系塔底弯矩对比

图7 4种结构体系桩基最大弯矩对比

由图4～图7可以得出以下结论。

(1)由于结构体系对于纵向约束改变较多，对于横向约束改变较少，结构体系对于纵向位移影响较大，对于横向位移影响较小。在地震作用下，主梁纵向位移在设固定支座的半漂浮体系与刚构体系较小，最大达到0.202 m，远小于全漂浮体系与仅设竖向支座的半漂浮体系；横向位移仅全漂浮体系较大，其他体系位移曲线几乎完全重合。

(2)高塔由于纵横向刚度均小于低塔，在地震作用下，高塔塔顶位移大于低塔，但高低塔塔顶位移规律一致。其中，塔顶纵向位移在全漂浮体系下最大为0.369 m，在仅设竖向支座的半漂浮体系下最大为0.354 m，在设固定支座的半漂浮体系下最大为0.202 m，在刚构体系下最大为0.153 m，由于设固定支座的半漂浮体系与刚构体系在纵向存在约束，其纵向位移远小于全漂浮体系与仅设竖向支座的半漂浮体系。

(3)结构体系对于塔底纵向弯矩影响较大，对于横向弯矩影响较小。对于纵向弯矩，仅在高塔设固定支座的半漂浮体系下，低塔塔底弯矩存在突变变小，使结构整体而言受力降低；对于横向弯矩在全漂浮体系下弯矩最小，其他体系较为接近。

(4)桩基内力纵向最大弯矩在设固定支座的半漂浮体系下最小，仅为4 960 kN·m，整体小于其他体系。横向弯矩在设固定支座的半漂浮体系下较大，达到6 054 kN·m，但整体小于刚构体系。

高速铁路无缝钢轨对于桥梁结构变形要求高，主梁纵向变形小的桥梁结构更适用于高速铁路[18]。针对地震作用对结构影响进行对比分析，以上4种结构体系，最合理的结构体系为体系3，即设置固定支座的半漂浮体系：塔梁分离，一个塔采用固定支座，另一个塔采用活动铰支座。主梁、塔顶位移较小，塔底、桩基纵向弯矩较小，总体而言，结构体系3结构抗震性能最优。

3.2 固定支座设置位置影响分析

结合该桥的支座设置，将活动支座与横向抗风支座结合，视作设置固定支座的半漂浮体系。该结构体系在地震作用下，由于不对称约束会造成惯性力传递的极不均匀，从而使两塔的地震反应内力相差悬殊，甚至会有几倍的差距；同时，对于高低塔斜拉桥而言，由于结构本身的不对称性，结构受力及变形也存在不对称情况。因此，应对固定支座位置进行探讨，确保结构处于最合理的受力状态，充分发挥出结构本身的抗震能力。

考虑两种不同固定支座设置位置：工况一为固定支座设置在高塔；工况2为固定支座设置在低塔，主梁及塔顶位移、塔底及桩基弯矩等结构状态，如图8～图11所示。

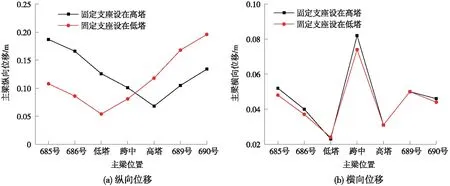
图8 主梁位移对比

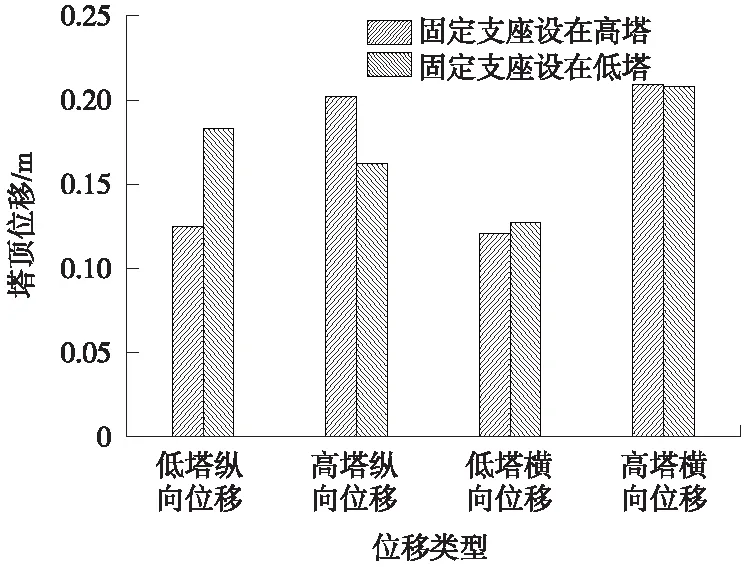
图9 塔顶位移对比

图10 塔底弯矩对比

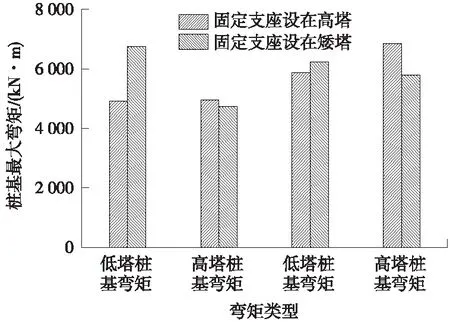
图11 桩基弯矩对比

由图8～图11可以得出以下结论。

(1)由图8、图9可以看出：固定支座设置位置对于结构纵向位移存在影响，对于横向位移几乎不产生影响。对比在高塔、低塔上设置固定支座，主梁纵向位移在固定支座处最小，远离固定支座增大，固定支座设置在高塔上，低塔侧梁端纵向位移最大可达到0.202 m，固定支座设置在低塔上，高塔侧梁端纵向位移最大可达到0.209 m，二者相差较小；塔顶纵向位移与主梁规律相反，在高塔设置固定支座，高塔塔顶位移最大达到0.202 m，在低塔设置固定支座，低塔塔顶位移最大达到0.183 m。主梁横向位移曲线、塔顶位移几乎完全重合，固定支座位置设置对其无影响。

(2)由图10、图11可以看出：与结构变形规律类似，固定支座设置位置对结构纵向弯矩存在影响，对横向弯矩几乎不产生影响。固定支座位置处桥塔、桩基纵向弯矩较大，设置在高塔，低塔塔底弯矩为233 305 kN·m，桩基弯矩4 911 kN·m，高塔塔底弯矩为505 475 kN·m，桩基弯矩为4 960 kN·m；设置在低塔，低塔塔底弯矩为436 398 kN·m，桩基弯矩为6 749 kN·m，高塔塔底弯矩为287 824 kN·m，桩基弯矩为4 738 kN·m。对比发现，与高塔设置固定支座相比，低塔设置固定支座后，塔底最大弯矩降低13%，桩基最大弯矩增加36%。但对于高低塔斜拉桥而言，桥塔本身抗震能力不同，高塔塔底屈服弯矩比低塔大15%，因此，固定支座设置在高塔更加能发挥结构内力方面抗震能力。

对于固定支座设置位置综合考虑，其设置位置对于结构极限变形影响相对而言较小，对于内力影响较大。设置在高塔，主塔桩基弯矩更小，虽然塔底弯矩更大，但考虑最大弯矩发生在高塔，结构屈服弯矩同样较大，可抵消该处更大弯矩，因此，可考虑将固定支座设置在高塔。

同时，结合结构体系选择与固定支座位置选择，可以看出，结构纵向约束的改变对于横向受力与变形影响较小，可近似忽略不计。

3.3 阻尼器参数影响分析

由于结构在罕遇地震作用下支座纵桥向受力过大，支座存在剪坏风险，阻尼器对大部分抗震能取得很好的减震效果[19-20]，应设置纵向阻尼器发挥作用，保证结构满足TB 10095—2020《铁路斜拉桥设计规范》要求。因此，应在桥塔上设置阻尼器进行支座位置抗震，同时对结构产生减震效应。

地震作用下，结构动力学方程为

(1)

式中，[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；[x]为位移向量；[Fg]为地震激振力向量；[Fd]为阻尼器提供的阻尼力。

阻尼力Fd与结构地震响应存在极大影响，非线性黏滞阻尼器的阻尼力与相对速度的关系为

Fd=CVα

(2)

式中，Fd为阻尼器提供的阻尼力；C为阻尼常数；V为速度；α为阻尼指数。

采用阻尼器作为减震措施，在罕遇地震作用下阻尼器发生作用，由式(1)、式(2)可以看出，其主要设计参数为阻尼常数C和阻尼指数α，其参数选取决定了结构减震效果。因此，应对于阻尼器不同设计参数进行对比分析，确定阻尼器的合理设计参数。通过参考类似设计，结构阻尼常数在2 000～5 000 kN/(m/s)中取值，阻尼指数在0.2～0.5中取值，对比阻尼常数2 000，3 000，4 000，5 000 kN/(m/s)，阻尼指数0.2、0.3、0.4、0.5，可以得出阻尼器参数与梁端纵向位移、塔顶位移及结构弯矩等目标函数的关系，如图12～图14所示。

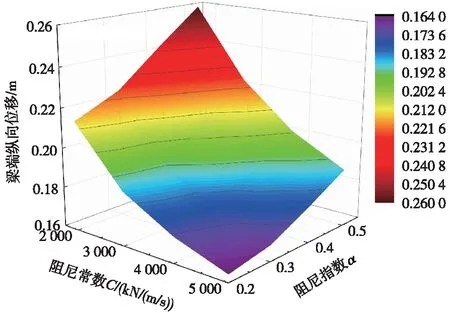
图12 阻尼器参数与梁端纵向位移关系

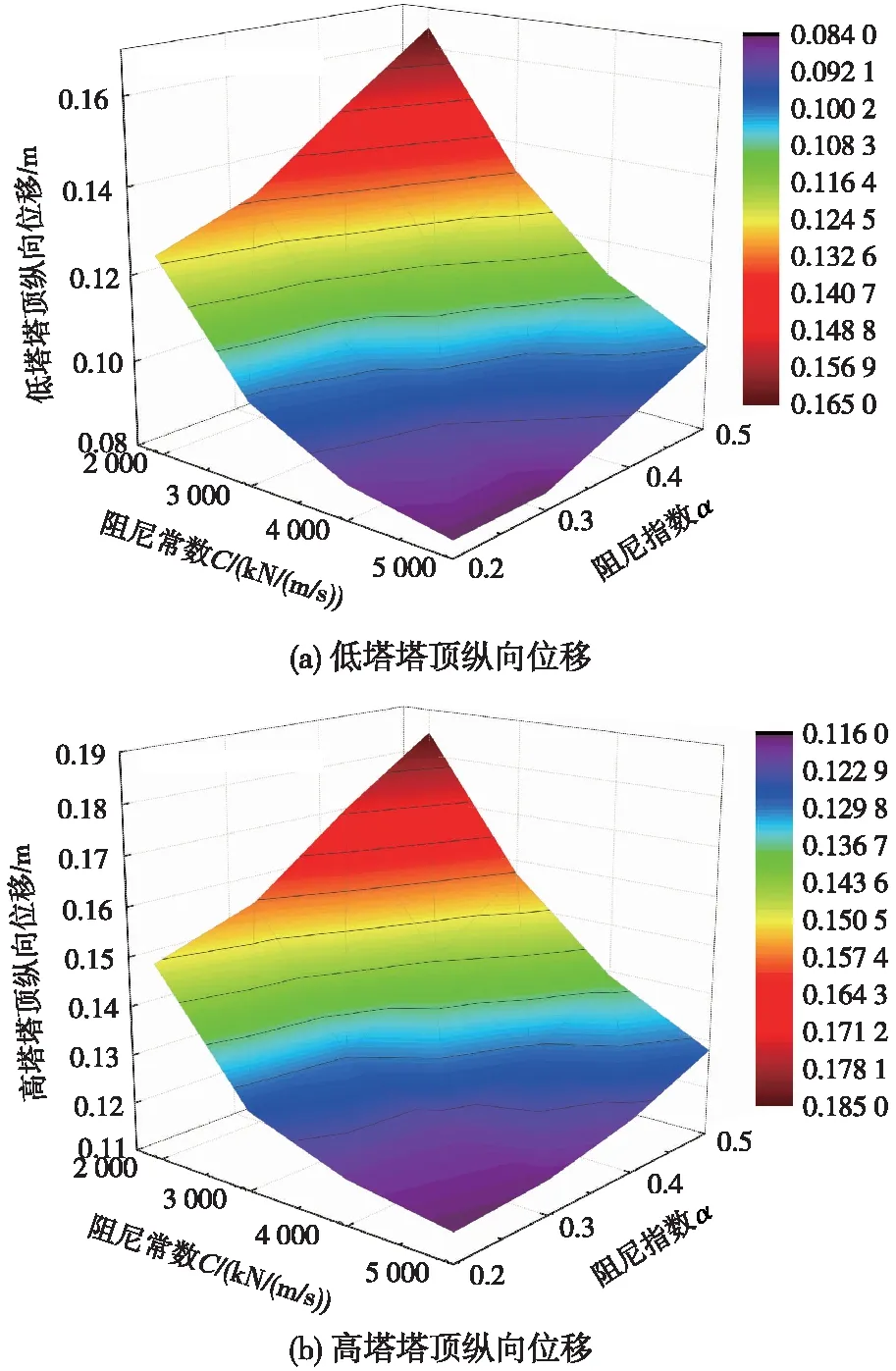
图13 阻尼器参数与塔顶位移关系

图14 阻尼器参数与塔底弯矩关系

由图12、图13可以看出，在阻尼常数取值2 000～5 000 kN/(m/s)，阻尼指数取值0.2～0.5范围内，结构位移随着阻尼常数增大、阻尼指数减小而减小，且变化趋势越来越慢。其中主梁梁端位移由最大值0.26 m降至最小值0.164 m，降低了37%；低塔塔顶位移由最大值0.165 m降至最小值0.084 m，降低了49%；高塔塔顶位移由最大值0.185 m降至最小值0.116 m，降低了37%。

由图14可知，在阻尼常数2 000～5 000 kN/(m/s)，阻尼指数0.2～0.5范围内，低塔塔底弯矩由最大值279 052 kN·m降至最小值178 775 kN·m，降低了36%；高塔塔底弯矩由最大值250 618 kN·m降至最小值185 408 kN·m，降低了26%。低塔塔底弯矩随着阻尼常数增大、阻尼指数减小而减小，且趋势越来越缓慢；高塔塔底弯矩随着阻尼常数增大、阻尼指数减小而先减小后增大，在C=4 000 kN/(m/s)，α=0.3时达到最小值。同时，桩基弯矩变化规律与塔底弯矩变化规律一致，随着阻尼常数增大、阻尼指数减小而减小，桩基弯矩由5 473 kN·m降至4 595 kN·m，降低16%。

综合对比结构位移与受力情况，罕遇地震下，结构在阻尼器参数C=4 000 kN/(m/s)，α=0.3时，受力与变形均较小，最为经济合理。

4 结构抗震性能分析

4.1 抗震设防目标

根据TB 10095—2020《铁路斜拉桥设计规范》中关于斜拉桥抗震要求，铁路斜拉桥采用两阶段设计、两水准设防的抗震设计方法，即设计地震及罕遇地震两种地震工况下的设计，结构在中震作用下保持整体弹性，在大震作用下保持主体结构基本弹性，修复后可使用[21]。基于桥梁抗震设防的合理安全度原则，颍河斜拉桥的抗震性能采用如表2所示抗震设防标准。

表2 抗震设防标准

4.2 动力特性

本桥采用多重Ritz向量法计算全桥动力特性，见表3。

表3 结构自振频率及相应特性

由表3可知：(1)本桥设置了纵向约束支座，颍河斜拉桥模型未出现纵漂振型；(2)主塔一阶横弯频率大于一阶纵弯频率，说明桥塔横向刚度大于纵向刚度；(3)主梁一阶横弯频率大于一阶竖弯频率，说明主梁面外刚度大于面内刚度。

4.3 地震响应分析

经过结构体系、固定支座设置位置以及阻尼器参数选择，确定最终合理斜拉桥结构设计。根据抗震设防目标主塔在设计地震作用下应保持弹性工作状态，在罕遇地震作用下应保持基本弹性工作状态。结构在设计地震作用下纵向约束发挥作用，在罕遇地震作用下纵向约束失效，由阻尼器发挥作用，设计地震与罕遇地震作用下桥塔弯矩如表4、表5所示。

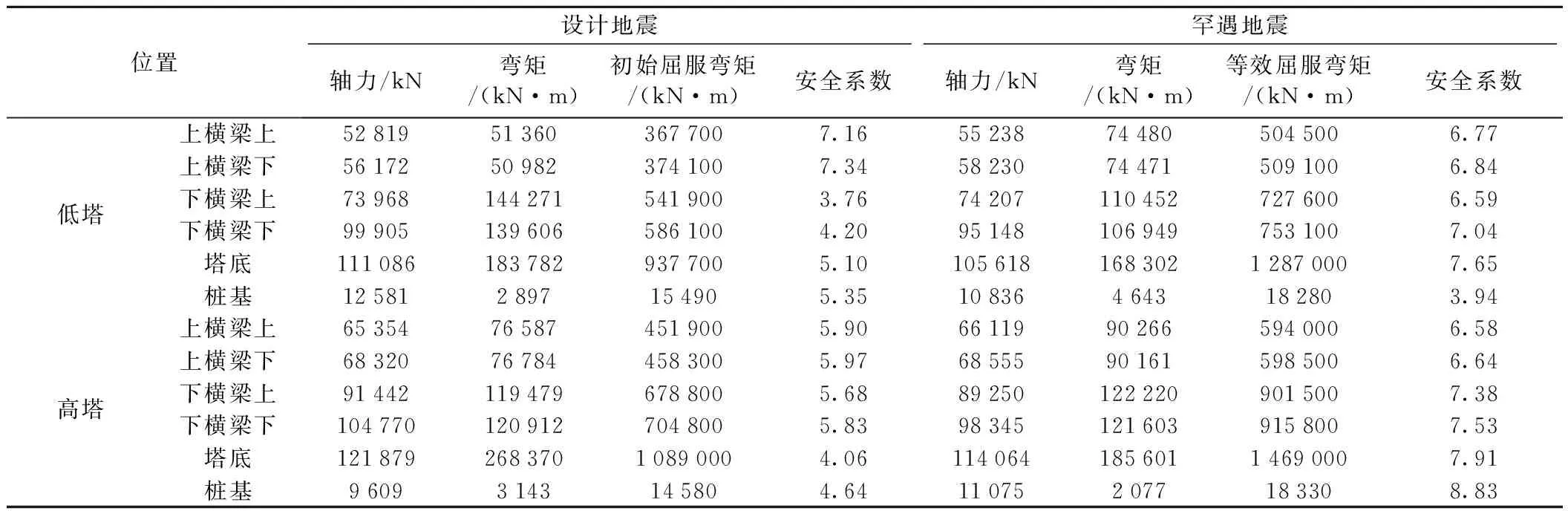
表4 纵向地震作用下抗震验算

表5 横向地震作用下抗震验算

由表4、表5计算结果可知，在设计地震作用下，主塔弯矩最不利截面弯矩均小于截面初始屈服弯矩，均保持在弹性范围之内，满足抗震性能要求。在罕遇地震作用下，主塔弯矩最不利截面弯矩均小于截面等效屈服弯矩，满足结构抗震性能要求。

5 结论

以阜淮高铁颍河高低塔斜拉桥为例，通过分析对比其在罕遇地震作用下不同结构体系、固定支座布置位置以及阻尼器参数选取，并进行斜拉桥抗震性能分析，得出以下结论。

(1)在罕遇地震作用下，全漂浮体系及仅设竖向支撑的半漂浮体系会导致过大位移，固结体系会导致过大的内力，设置固定支座的半漂浮体系可以更好地发挥结构的抗震性能。

(2)对于该半漂浮体系高低塔斜拉桥，宜在高塔处设置纵向约束，可以更加有效地发挥结构抗震性能。

(3)阻尼器对于结构本身存在很好的减震作用，对于阻尼器参数的选取，应根据结构在罕遇地震下的变形与内力共同确定，在阻尼常数2 000～5 000 kN/(m/s)，阻尼指数0.2～0.5范围内，结构位移以及弯矩整体而言均随着阻尼常数增大、阻尼指数减小而减小，对于该桥而言，在C=4 000 kN/(m/s)，α=0.3时，结构抗震性能与性价比最优。

(4)该桥在设计地震作用下处于弹性工作状态，在罕遇地震作用下处于基本弹性工作状态，抗震性能满足规范要求。