基于前馈补偿PI控制算法的液压排缆系统的研究

周 扬，朱煌庆，王志敏

（中国船舶集团第七一五研究所，杭州 310023）

0 引言

海洋绞车是海洋工程机械装备系统中的关键装备之一，主要应用于海洋管道铺设、水面及水下拖曳系统、海洋资源钻探等领域[1]，其最关键的技术在于缆绳的收放过程的控制。缆绳的收放过程控制一般通过海洋绞车的排缆机构实现，因此排缆机构的设计是海洋绞车设计中的关键技术。排缆机构选型或者参数设计不合理，易出现排缆不齐、骑缆、跳缆、相互挤压的等状况，不仅大大降低海洋绞车的收放速度及收放效率，而且会加剧缆绳的磨损进而影响缆绳的寿命，严重时甚至关系到整套系统能否顺利完成作业。

根据驱动方式的不同，排缆机构可以分为机械式排缆机构、液压排缆机构和电驱动排缆机构[2]。机械式排缆机构即通过链条或齿轮等方式，将驱动绞车的动力传递至排缆机构，通过精确计算设计传动比，使得排缆机构和绞车同步运行，从而实现自动排缆。现实设计中通常采用绞车卷筒输出轴端安装驱动链轮，通过链条带动排缆机构双头丝杠进而实现往复排缆，通常用于单一缆径的海洋绞车；液压排缆机构即通过液压系统驱动滚珠丝杆带动排缆机构运动，通过精确控制使得排缆机构和海洋绞车同步运行[3]。现实设计中通常采用滚珠丝杠一侧安装液压马达，丝杠另一侧安装角度编码器，通过排缆机构液压系统中的比例换向阀精确控制液压马达的转速，进而实现海洋绞车与排缆机构的运行速度匹配，从而实现自动排缆，可用于不同缆径的海洋绞车[4]；电驱动排缆机构即通过步进电机或者伺服电机驱动滚珠丝杆带动排缆机构运动，其与液压排缆机构驱动方式不同，控制原理相似。3 种驱动方式各有优缺点，依据装备和功能不同进行灵活选用[5]。

对于排缆机构的控制算法，常规PID 控制较为成熟且应用广泛，但抗干扰能力较差，且无法适应大范围调速的绞车工况。滑模控制对系统参数变化及外界扰动不敏感，但控制器输出“抖颤”问题无法解决，有可能导致系统不稳定[6-7]。

本文针对采用液压排缆机构的海洋绞车，针对性的分析了绞车与排缆机构运行的速比关系，并设计了采用基于前馈补偿的PI 控制算法的排缆机构液压系统。该控制算法实现简单、控制精度高，可在大范围调速时仍然取得较好的排缆效果，具有十分重要的应用价值。

1 液压驱动排缆机构设计

某海洋绞车为液压驱动绞车，此绞车用于收放及存储数千米长的缆绳，因此在缆绳完全回收后，缆绳排列层数多；缆绳在收放过程中承受较大的张力，且在海洋多变工况下，可能对排缆机构产生一定的侧向力；整根缆绳由两种规格直径的缆绳在中间某位置连接而成，因此缆绳为变径缆绳；同时此海洋绞车对缆绳的最高及最低稳定收放速度差异范围较大，属于大范围调速的绞车。基于以上现实条件，为了使整个海洋绞车系统构成合理，排缆控制效果优良，设计了基于比例换向阀控制的液压马达驱动的排缆机构[8-9]。其液压原理如图1所示。

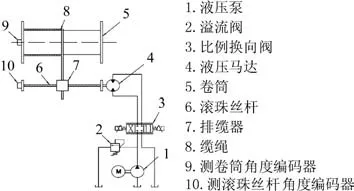
图1 排缆机构液压原理

排缆机构液压系统由液压泵1 进行供油，系统压力由溢流阀2 进行设定，通过比例换向阀3 控制液压马达4 的转动方向及转动速度，液压马达4 驱动滚珠丝杆6 转动，滚珠丝杆6 的旋转运动带动排缆器7 左右横移，实现绞车缆绳的自动排缆；5 为绞车卷筒，8 为卷筒上缆绳，9 为测卷筒转动角度编码器，10为测滚珠丝杆转动角度编码器。

系统工作时，绞车卷筒转动，通过编码器9 可以测定卷筒的累计转动脉冲数，通过计算可以得出此时缆绳所在的具体排缆位置。为使缆绳排列紧密且整齐，排缆器需要移动到对应位置，此时控制器输出控制信号控制比例换向阀的开口和方向驱动液压马达转动，带动排缆器运动到对应位置，编码器10 可以检测滚珠丝杆转动脉冲数从而计算排缆器的实际位置，从而使排缆器能始终精确运动跟随到缆绳的排缆位置。

2 排缆机构运动控制算法

2.1 PID算法的缺陷

PID算法为一种基于反馈的闭环控制算法，是按偏差的比例、积分和微分进行控制，为一种广泛应用的自动控制原理[6]。

在该系统中，这个反馈就是滚珠丝杠角度编码器，返回给控制器计算当前排缆器的位置。用这个反馈计算得出的排缆器位置跟卷筒角度编码器脉冲计算得出的缆绳排缆位置进行比较，如果位置偏差过大，就加大比例阀换向阀的开口，相反则减小开口。

在该系统中，卷筒最大速度和最小速度差距较大，约15倍左右，再加上该卷筒上缆绳有两种直径的规格尺寸，两种缆绳直径差距约2 倍。因此在整个缆绳收放过程中，排缆机构要求的最小运动速度和最大运动速度差距在30 倍以上。由于该系统采用比例换向阀控制液压马达完成排缆机构的运动，而比例换向阀开口在小范围变动时流量可近似线性，但其开口在大范围变化时流量具有非常强的非线性[10]。因此，若直接应用PID 算法，其固定一组参数只能满足卷筒小范围调速工况下的精确跟随。当绞车在大范围调速工况下时，PID 算法的比例参数无法满足排缆机构稳定精准跟随的要求，易导致绞车排缆机构出现超前或者滞后的情况，使得绞车在进行急加速或急减速时易出现跳缆或骑缆现象，或者导致在某个速度范围内出现系统不稳定现象，影响收放作业。

2.2 基于前馈补偿的PI控制算法

所谓前馈补偿是在系统中增加一个控制环节，使得该控制环节与系统的传递函数乘积为1，其本质是开环控制[11]。在实际系统中，由于各种干扰因素的存在，单独前馈补偿很难做到理想情况使得系统进行高精度稳定地控制。然而，当前馈补偿与反馈控制相结合的时候，则可以发挥两者的优势，使得控制效果更加快速和精准。

前馈补偿+反馈控制的结构如图2 所示。其中Gr（s）为前馈补偿传递函数，Gp（s）为反馈控制算法传递函数。前馈补偿可以有效消除系统扰动带来的影响，使得控制更为精准，鲁棒性更强。

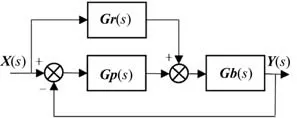
图2 前馈补偿+反馈控制结构

在该系统中，最大的扰动来自于卷筒速度的变化，因此将该扰动引起控制变动进行补偿。

（1）排缆误差计算

假设卷筒上缆绳在第i层，以左侧为零点，要想排满该层缆绳卷筒转动总脉冲为Ni，卷筒宽度为X，当前时刻卷筒脉冲为Nt，不难算出此时缆绳应该在X的位置。滚珠丝杠宽度为Y，排缆机构全行程移动滚珠丝杆转动脉冲变化为n，当前时刻滚珠丝杆转动脉冲数为nt，不难算出此时排缆器所在位置为。因此排缆误差如式（1）所示：

式中：Nt为卷筒当前脉冲；Ni为排满该层卷筒转动总脉冲；X为卷筒宽度；nt为当前时刻滚珠丝杠脉冲；n为排缆机构全行程移动滚珠丝杆转动脉冲；Y为滚珠丝杠宽度。

（2）前馈补偿量的计算

假设用参数NV表示卷筒每秒转动编码器计数，则此时缆绳横向移动速度为，通过摸底试验可以得到比例换向阀控制量与排缆器移动速度的对应关系，w=f(v)，其中w表示比例换向阀的控制量，v表示排缆器移动速度。因此前馈补偿量如式（2）所示：

式中：NV为卷筒每秒转动脉冲；Ni为排满该层卷筒转动总脉冲；X为卷筒宽度。

（3）比例换向阀控制函数

由式（1）和（2）的分析计算得到比例换向阀的控制函数如式（3）所示：

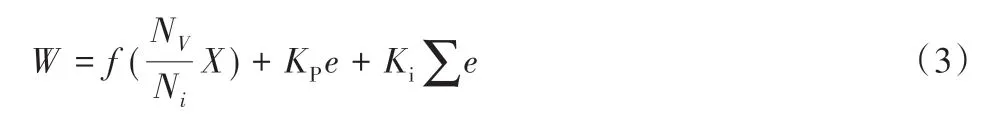
式中：f()前馈补偿量；KPe为P 控制量；为I 控制量；KP和Ki分别为P控制参数和I控制参数。

3 排缆系统控制算法仿真研究

利用软件建立该排缆系统仿真模型，如图3所示。

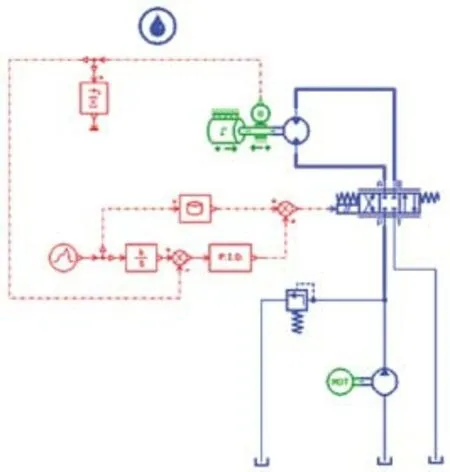
图3 液压系统仿真模型

在该模型中，按照实际液压系统原理图建立了模型，而对于卷筒和排缆机构则进行了简化，将实际系统中编码器信号数字化。同时建立了上述基于前馈补偿的PI 控制模型。对该系统进行仿真，得到如下结果。

在图4 中，红色曲线代表马达转动角度目标控制曲线，绿色曲线代表实际控制曲线。马达运动过程中，经历了低速运转阶段0～10 s 阶段，转速约为3 r/min，为最高转速的3%；中速运转阶段，10～35 s 阶段；最高速运转阶段，35～50 s；不同运转阶段的速度切换均在1 s 之内完成。图5 为控制目标值和实际值的偏差。通过图4 和图5 发现系统的跟踪误差较小，最大误差约为120°，且在较小时间内误差进一步减小。由于仿真过程中设置的加减速过程条件比实际系统中更为苛刻，所以实际系统中运行误差更小。在图6 所示为马达实际运行转速，曲线显示马达运行平稳，无论是低速、中速和高速阶段，系统均能平稳无抖动运行，且系统速度切换过程中也能较快地稳定转速。总体来说，该控制算法能使得排缆器在大范围调速工况下，精确稳定地运行，取得较好的控制效果。

图4 马达转动角度目标与实际控制曲线

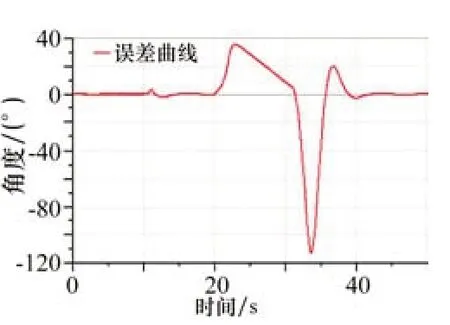
图5 马达转动角度目标与实际控制角度误差值

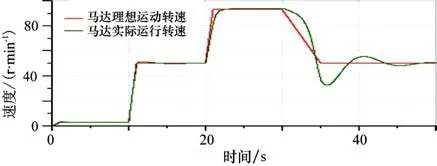
图6 马达实际运行转速

后续在海洋绞车的研发生产过程中采用了此算法进行了测试，取得理想的控制效果。海洋绞车在低速、中速和高速收放过程中排缆器能快速准确地跟随，在卷筒急加速及急减速等大范围调速工况的过程中也能稳定且准确地跟随，控制效果良好。

4 结束语

本文简单介绍了海洋绞车设计中的关键技术，分析了某液压驱动海洋绞车的排缆工况和需求，并设计了基于比例换向阀控制的液压马达驱动的排缆机构，分析了采用常规PID 控制算法的缺陷及易导致的问题，并提出了基于前馈补偿的PI 控制算法。对基于该算法的排缆系统建立模型并进行了仿真计算，仿真结果表明，该控制算法在海洋绞车各种速度工况下均能取得较好的控制效果，控制精度高，系统稳定性好。不足之处在于为取得更好的控制效果，进行前馈补偿时通过摸底试验提前得到开环情况下比例阀控制信号与排缆器运动速度之间的关系，使得此海洋绞车研发过程中调试工作量有所增加。