基于螺距约束和HPSOGA算法的六自由度焊接机器人路径规划

掌俊玮，张礼华，蒋雨洋，李家富，李晨洁

(江苏科技大学 机械工程学院 镇江 212100)

在焊接作业中，大多焊接接头以不规则的分布呈现，而机器人对焊点次序的选择，将会影响其焊接效率[1].传统的路径规划方法往往依赖于人工规划，很难保证最优解，容易导致耗时长、生产率降低等一些问题[2].智能算法能够提供一种有效的方法避免人工规划，进而获取最优解.遗传算法(GA)和粒子群算法(PSO)是这类智能算法中的典型代表[3-6].遗传算法是一种并行的、随机的全局搜索优化方法，选用继承、突变和交叉等生物学技术，模拟生物进化机制的迭代过程，具备较强的适应性和较为优异的计算性能等优点.粒子群算法由于简单、容易实现，且参数较少，在实数编码问题上具有良好的性能[4].将遗传算法和粒子群算法进行恰当的混合，不仅可以提高粒子群的算法的粒子多样性，还可以保留变异操作，优化遗传算法的全局搜索能力.文献[7]在粒子群算法中下一代粒子的生成中引入遗传算法提高粒子多样性，设计了HPSOGA算法解决机器人的逆运动学求解问题，具有较好的性能.文献[8]在解决机器的调度优化问题时，通过聚类将GA算法和PSO算法结合，当GA算法被先执行时，能够有效提高HPSOGA算法的全局搜索能力. 在文献[9]中，将HPSOGA算法用于解决焊接机器人的路径规划问题，并表明HPSOGA算法具有较强的搜索能力和实用性.受文献[10]启发，在翅片管与汇集箱的焊点路径规划问题中，引入螺距约束进行描述多个翅片管焊点间的关系，并设计了带有螺距约束的HPSOGA算法，搜索机械臂的焊接最短路径.

1 机械臂动力学分析

在翅片管和汇集箱的焊接问题中，根据对焊接工艺的分析，选用六自由度机械臂.如图1，将六自由度机械臂放入D-H坐标系，进行动力学分析，得到六自由度机械臂的D-H参数，如表1:αi-1、ai-1、θi-1分别为连杆的扭角、长度、转角，di-1为关节距离.

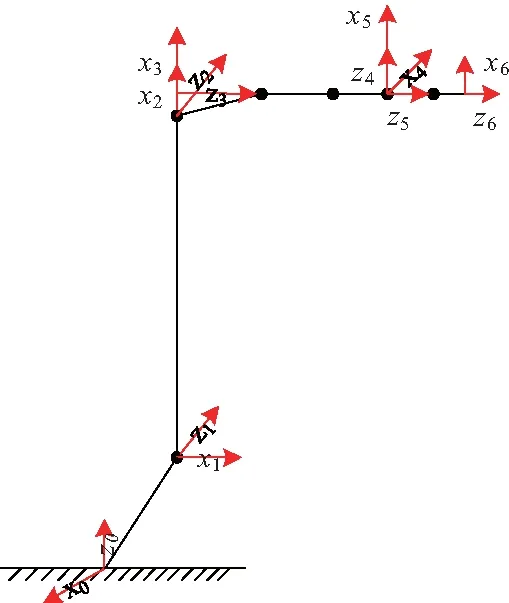
图1 机械臂D-H坐标系

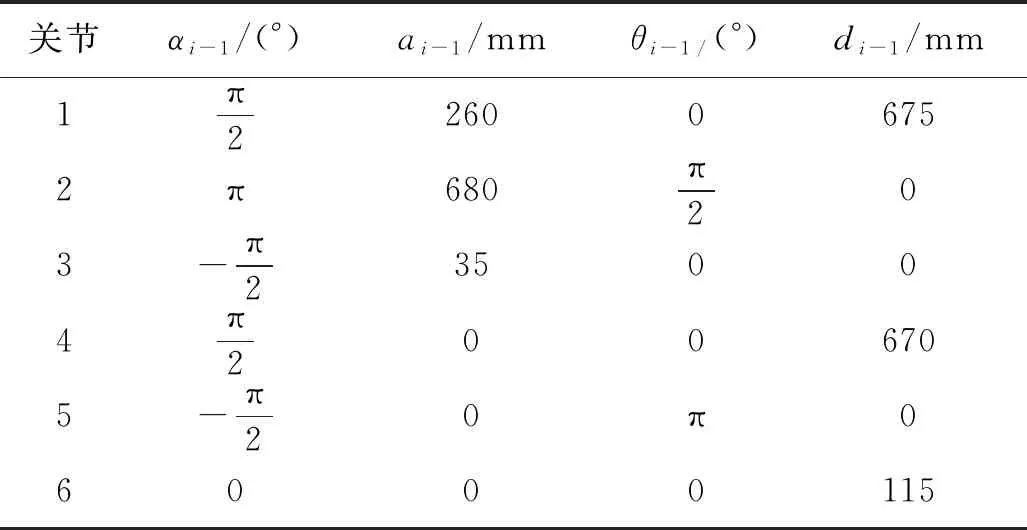
表1 焊接机械臂的D-H参数

设机械臂节点i的坐标系{i}变换到机械臂节点i-1坐标系{i-1}的矩阵记为i-1Ti，则节点i到节点i-1的变换矩阵可以描述为：

i-1Ti=R(xi-1,αi-1)T(xi-1,ai-1)R(zi-1,θi)T(zi,di)=

(1)

式中：R(xi-1,αi-1)为绕xi-1转动αi-1角的矩阵；T(xi-1,ai)为沿着xi-1移动ai-1的矩阵；R(zi,θi)为绕着zi转动θi角的矩阵；T(zi-1,di)为沿着xi-1移动ai-1的矩阵.

设机械臂末端位姿的变换矩阵为0T6，可以描述为：

0T6=0T1·1T2·2T3·3T4·4T5·5T6=

(2)

其中，

将设计的焊接机械臂的D-H参数带入式(2)，根据正运动学矩阵变换关系，机械臂位于空间中某一种位姿时，可以计算每个关节的角度值，进而可以确认出位姿矩阵0T6的具体参数，求解机械臂末端位姿.

2 基于HPSOGA算法的路径规划

2.1 问题描述

螺距是指两螺旋线上对应点间的距离.在焊接工件时，第i根翅片管与汇集箱的焊接轨迹i以及第i+1根翅片管与汇集箱的焊接轨迹受螺距约束，如图2.

图2 工件焊接时轨迹间的螺距

(3)

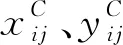
(4)

式中：c=cos(angle)，s=sin(angle)，angle为矢量(x,y,z)的正向看去逆时针旋转得到的角度，且矢量(x,y,z)必须是单位化且经过原点.

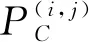
(5)

式中：r为机械臂的半径；n为焊点P的法向量在机械臂平面上的投影矢量，且是单位向量.

考虑第i根翅片管与汇集箱的焊接任务P={Pi}，则第i根翅片管与汇集箱的焊接轨迹i以及第i+1根翅片管与汇集箱的焊接路径可以描述为：

(6)

则机械臂的路径规划的目的时，搜索最短的焊接头序列，使得机械臂在起始焊点到目标焊点的总路径最小.当焊接路径为Path时，机械臂的焊接距离f(Path)可以描述为：

(7)

2.2 基于HPSOGA算法的焊接路径规划

在传统的PSO算法中，粒子状态在t时刻的更新过程可以描述为：

(8)

式中：ω为惯性权重；C1和C2为学习因子；r1和r2为0～1间均匀分布的随机数；i为粒子索引.

随着时间的增长，每个粒子会不断的更新局部最优解pbest和全局最优解gbest,逐渐会收敛到pbest或gbest.当pbest和gbest陷入局部最优解后，则粒子最终也将陷入局部最优解，很难获得真正的全局最优解.基于此，同时采用GA算法来搜索全局最优解gbestGA，当PSO算法陷入局部最优解时，将GA算法获取的gbestGA，作为全局最优解更新粒子状态，因此HPSOGA算法中的粒子状态更新过程可以设计为：

(9)

式中：GA(k)为第t时刻迭代时的采用GA算法获取的全局最优解；r1、r2、r3服从均匀分布[0,1].

在实际中，工程问题往往是离散的.为了解决翅片管与汇集箱的焊接路径规划问题，借鉴文献[11],引入交换算子和交换序列，将HPSOGA算法中的粒子的更新过程式(9)进行离散化，可得：

(10)

(11)

(12)

式中：D为粒子群的长度.

3 仿真实验

仿真采用六自由度机械臂焊接翅片管与汇集箱，如图3，在matlab导入solidwork模型进行仿真，假设机械臂在初始位置的关节角度q0=[π/2,-π/2,0,0,0,0]，则机械臂的末端位姿0T6根据运动学求解可得：

图3 六自由度机械臂初始位置

为了便于对比，分别采用PSO算法、GA算法、HPSOGA算法求解翅片管与汇集箱的最优焊接路径，其初始参数设置：

PSO算法的粒子数目为2 000个迭代次数设为1 000次，GA算法的种群数目为2 000个，迭代次数为1 000代，在HPSOGA算法中，PSO的迭代次数为40，GA的迭代次数为200.同时，GA算法和HPSOGA算法中的交叉概率取0.93，

变异概率取0.06，PSO算法和HPSOGA算法的学习因子取C1=1.496 2、C1=0.582 5，分别运行3种算法20次，对实验结果进行加权平均处理.图4为3种算法的收敛速度曲线，可以看出HPSOGA的收敛速度最快，当达到值时，获取最优解；PSO算法的收敛速度要微快于GA算法.

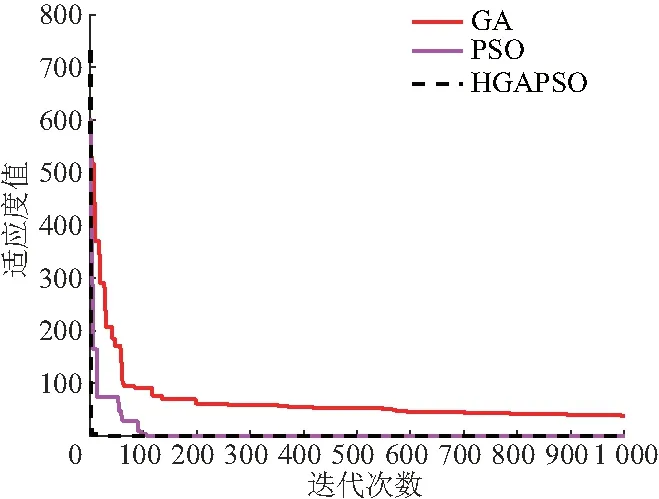
图4 3种算法的收敛速度

图5为HPSOGA算法获得的较好焊接路径.

图5 HPSOGA路径规划结果

4 结论

(1) 对六自由度机械臂进行动力学分析，建立六自由度机械臂的动力学模型，并求解其D-H参数.

(2) 在解决带有螺距约束的焊接问题中，将遗传算法和粒子群算法进行恰当的混合，提高粒子群算法的粒子多样性，通过变异操作优化遗传算法的全局搜索能力，并运用交换算子和交换序列对粒子状态的更新过程进行离散化.

(3) 在matlab中导入solidworks模型，搭建算法仿真平台，分别采用PSO算法、GA算法、HPSOGA算法进行路径搜索，经过多次实验表明，在本文所设计的算法下，机械臂能够获得较为平滑的焊接轨迹，且焊点路径最短，进而验证了该算法的有效性和正确性.