面向交通流量预测隐私保护的联邦学习方法

傅思敏 王 健 鹿全礼 赵阳阳

1(北京交通大学计算机与信息技术学院 北京 100044)

2(山东正中信息技术股份有限公司 济南 250014)

3(山东省数字化应用科学研究院有限公司 济南 250102)

(972846267@qq.com)

1 研究背景与现状

准确高效的交通流量预测对于帮助交通管理机构缓解交通拥堵，帮助大众规划路线、高效出行具有重要意义.由于交通流量的随机性和非线性，准确实时的交通流量预测仍然是一个挑战.近年来，学者们尝试用深度学习来解决这一时间序列预测问题，并取得了较好的效果[1-3].在基于深度学习的方法中，循环神经网络被证实比一些常用的传统神经网络具有更好的性能.例如，2016年文献[4]首次使用门控循环单元(gated recurrent unit, GRU)神经网络对交通流量数据进行集中式训练与预测，并且取得了较好的效果.

然而，现实情况并非那么理想.目前国内大部分城市智能交通往往由几个机构同时负责，数据通常存储在机构本地.由于利益冲突以及企业之间的壁垒等，数据不能互联互通，形成了“数据孤岛”.此外，交通监测数据往往来自于传统摄像头图像采集、车载GPS设备采集等，这些信息本身就存在侵害大众隐私的风险[5]，采取集中存储方式也不妥当.

针对“数据孤岛”现象，谷歌于2016年提出联邦学习方式，给出了新的解决思路.联邦学习是一种客户端本地协作式训练思想，通过上传梯度而不是上传数据到服务器实现数据隐私保护.文献[6]提出一种面向数据隐私保护的联邦学习航空出行预测方法，融合高铁出行数据、第三方APP记录的居民消费数据进行联邦学习，提高了航空出行预测的准确性和可靠性.文献[7]将联邦学习和交通流量预测结合起来，解决了交通流量数据共享学习利用问题.

虽然联邦学习允许参与方在本地进行训练，避免了数据信息泄露风险,然而最近的研究表明，联邦学习并不总是能够提供足够的隐私保证.文献[8]从模型共享梯度中推断出了图像标签，并成功恢复出了原始训练样本.文献[9]根据人脸识别模型的训练结果较为准确地还原了原始数据，此攻击场景也适用于联邦学习.因此越来越多的研究工作开始聚焦于如何为联邦学习本身提供更为可靠的隐私保护.现有的梯度隐私保护方式分为加密类方法和扰动类方法.加密类方法主要利用密码学理论进行保护.文献[10]提出一种参数掩盖联邦学习隐私保护方案，该方案包含密钥交换、参数掩盖、掉线处理3个协议，能够抵御服务器攻击、用户攻击、服务器和少于t个用户的联合攻击.文献[11]介绍了智能电网中隐私保护的主要技术手段，包括现有密码学技术、安全多方计算在智能电网隐私保护方面的突破.数据扰动类方法主要采用差分隐私方式对梯度进行干扰.文献[12]基于随机梯度下降(stochastic gradient descent, SGD)算法过程可以是并行和异步的事实，提出协作式深度学习，并且基于差分隐私在噪声发送到服务器之前，将噪声注入参数中，通过选择性地交换模型的部分重要参数减轻隐私损失预算，达到实用性与隐私性的权衡.文献[13]提出一种针对参与方的差分隐私随机梯度下降算法，其目的是在模型训练阶段扰动参与方的模型更新参数，并且提出一种基于合成定理的隐私预算计算方法，称为时刻统计(moment accountant, MA)，为隐私损失提供了更为严格的界限.然而文献[13]也只是将差分隐私应用于传统的简单前馈神经网络.虽然已有研究将联邦学习应用于流量预测场景[7]，但未曾在梯度上进行隐私保护.总的来说，加密类方法虽然安全，但计算开销大、复杂度高、成本高；差分隐私之类的数据扰动法因其轻量化、消耗计算资源少、计算快速等特点，更加满足当前交通流量预测场景的准确性、实时性需求.

面向交通流量预测领域，针对各机构数据无法共享以及联邦学习训练过程中普通的参数梯度所面临的重构攻击问题，本文提出一种采用差分隐私进行数据保护的联邦学习方法.该方法不仅协调独立的各方共同训练，从而准确预测交通流量，而且使攻击者不能以高置信度推断出训练数据的特定信息，提供了更可靠的数据隐私保护.本文在实际交通流量数据集上进行对比实验，最终得到一组参数达到了较好的预测效果，在模型隐私性与可用性之间取得了一个平衡，体现了该方法的优越性与可行性.

2 面向交通流量预测隐私保护的联邦学习方法

2.1 总体框架

本文提出的面向交通流量预测隐私保护的联邦学习方法基于联邦学习框架，如图1所示.典型的联邦学习训练步骤如下[14]：首先，在训练之前，所有客户端商定一个共同的模型，包括神经网络的结构、特征，每个隐藏层的激活函数、损失函数等，商定之后将此模型部署在本地.本文模型为循环神经网络GRU模型，采用该模型进行交通流量预测.然后，云服务器随机初始化第1轮的全局模型参数(ωt，t=1)，并依次传递给各客户端，客户端在自己的私有数据集上训练模型，并将不同的私有梯度(Δωt+1)上传到服务器.之后，服务器对参数进行聚合，并更新全局模型参数，开始下一轮训练，依此类推，最终完成训练.

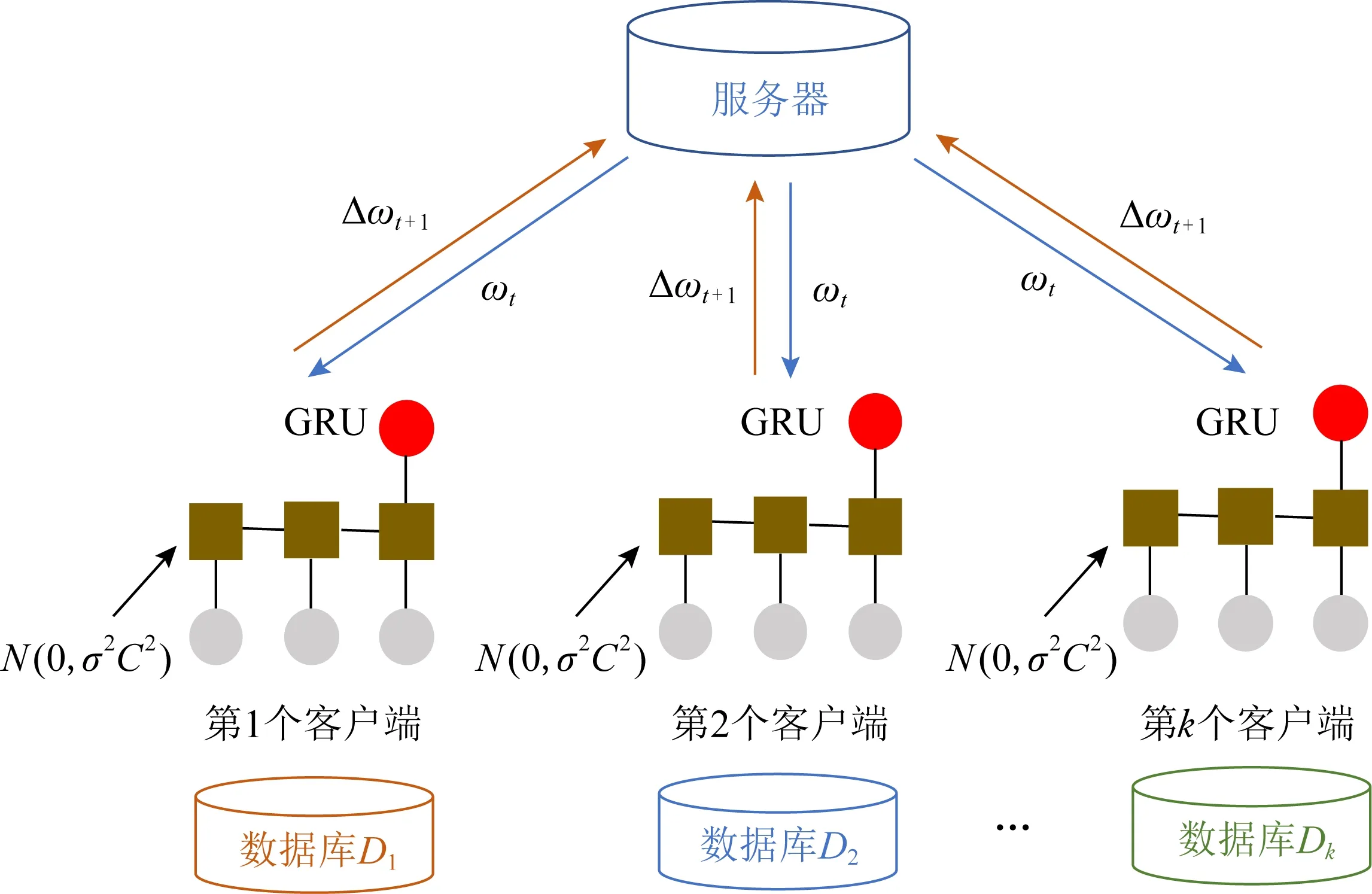
图1 联邦学习总体框架

2.2 客户端模型

客户端在本地对流量数据进行GRU模型训练.本地模型训练时，在反向传播过程中，向梯度添加计算好的高斯噪声.在全局迭代结束后，客户端算法最终满足(ε,δ)-差分隐私，上传的模型参数也具有随机性，从而成功防止被攻击者窃取.

2.2.1 符号说明

为了方便理解，对本文用到的符号进行说明，如表1所示.

2.2.2 客户端DP-GRU算法流程

将客户端本地添加了差分隐私的GRU算法称为DP-GRU算法.下面给出第k个客户端的DP-GRU算法，如算法1所示：

算法1.DP-GRU算法.

输入：D={x1,x2,…,xn}，ωt，T，E，L(ω)，C，(ε,δ)，η，q；

① Initializee=0;

表1 本文符号说明

② Initializeωe=ωt;

③σ=FedMA(ET,(ε,δ),q);

④ fore∈0,1,…,E-1 do

⑤ Take a random sample setXqwith

sampling probabilityq;

⑥ for eachxi∈Xqdo

⑦ge(xi)=∇L(ωe,xi);

⑨ end for

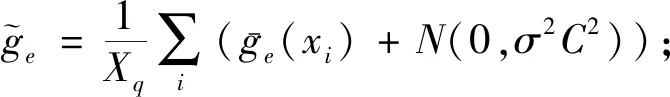
算法具体流程如下：

首先，(行①)初始化本地迭代次数变量e=0；(行②)客户端从服务器端接收全局模型，初始化本地模型参数ωe=ωt；(行③)客户端根据隐私预算计算算法FedMA计算本地要添加的高斯噪声标准差σ，FedMA算法的功能是借鉴MA机制对预添加的高斯噪声进行计算，使得客户端的DP-GRU算法最终满足(ε,δ)-差分隐私.

本地E轮迭代结束之后，(行)客户端得到全局第t+1轮本地模型参数ωE，(行)计算与初始化全局模型参数ωt相减的模型参数更新(行)将模型参数更新上传至服务器.

2.2.3 客户端差分隐私实现

当前深度学习差分隐私的主流应用模式有2种：一种是在本地模型训练结束后，选择重要的参数更新，在其上添加噪声[15]；另一种是在模型训练时，在反向传播过程中，给梯度添加高斯噪声[13].然而，正如Abadi等人[13]所考虑的，如果仅处理训练产生的最终模型参数，由于客户端对于这些参数与数据的依赖性，使得没有办法得到一个对参数与数据严格的界定方法.如果添加了过于保守的噪声，会破坏最终学习模型的效用.因此本文借鉴文献[13]的差分隐私随机梯度下降算法，选择在客户端本地GRU模型训练反向传播过程中，给梯度添加高斯噪声实现差分隐私，使攻击者无法通过干扰过的模型参数还原出训练数据，从而提供针对间接数据泄露的强大保护.

差分隐私定义如下：

定义1.(ε,δ)-差分隐私.给定一个随机算法M，D和D′是至多相差1条记录的相邻数据集.如果M在这2个数据集上的输出满足以下公式，则称M是(ε，δ)-差分隐私的.

Pr[M(D)∈S]≤eεPr[M(D′)∈S]+δ，

(1)

其中，Pr[M(D)∈S]表示M在D上的输出在值域S(S⊆Range(M))中的概率；ε称为隐私预算，它量化了算法的隐私保障水平，一般说来，ε值越小，在D和D′上输出的概率分布越接近，即M的隐私保护级别越高；隐私参数δ称为松弛因子，为算法不满足差分隐私的概率，通常设置为非常小的数字或0.

差分隐私一般通过在数据集的输出中添加噪声扰动实现，而要加入多少噪声与数据集的全局敏感度有关.全局敏感度定义如下：

定义2.全局敏感度Δf.对于任意给定的查询函数f，f的全局敏感度Δf为

(2)

在DP-GRU算法中，数据集D为客户端本地私有数据集，查询函数为梯度计算，查询输出为梯度.算法1的行⑧根据裁剪操作，将单个梯度的第二范式限制在C以内，从而保证了全局敏感度大小为C.

拉普拉斯机制和高斯机制是常用的2种差分隐私噪声机制[16]，这2种机制主要针对数值型数据.其中，高斯机制更为松弛，在实现隐私保护的基础上也能兼顾准确性，因为本文采用高斯机制实现差分隐私.

定义3.高斯机制.对于任意查询函数f和全局敏感度Δf，若随机算法M满足

M(D)=f(D)+N(0,σ2)，

(3)

且有

(4)

则称M满足(ε,δ)-差分隐私.其中，N(0,σ2)为添加的均值为0、方差为σ2的高斯噪声.

当前很多学者致力于研究特定噪声分布下的隐私预算.本文借鉴Abadi等人[13]提出的MA机制，在客户端训练过程中采用基于MA机制构建的FedMA算法对隐私预算进行计算，该机制对隐私预算提供了更严格的限制.采用FedMA算法可以根据提前设置好的隐私预算ε、松弛因子δ、添加噪声的步骤次数TE计算出相应的高斯噪声标准差σ.经过本地TE轮噪声添加，可以计算出更少的隐私预算，也即实现了(ε,δ)-差分隐私.目前开发者已公开了MA机制及相关算法，用户可以方便地在机器学习框架(如TensorFlow)中调用.

2.3 服务器端模型聚合

服务器端聚合客户端上传的模型参数更新，与上一轮的全局模型参数相加，从而得到下一轮的全局模型参数.服务器端模型聚合算法(Fed-DP-GRU)如算法2所示.算法输入为参加联邦学习模型训练的客户端集合zm、全局迭代次数T、分配给客户端的隐私预算ε以及松弛因子δ.

算法2.Fed-DP-GRU算法.

输入：zm，(ε,δ)，T；

输出：ωT.

① Initializeω0randomly;

② fort∈0,1,2,…,T-1 do

③ fork∈zminparallel do

⑤ end for

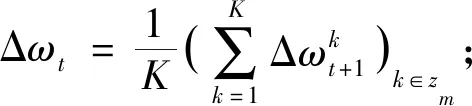
⑦ωt+1=ωt+Δωt;

⑧ end for

⑨ returnωT.

算法具体流程如下：

首先，(行①)随机初始化第1轮的全局模型参数ω0.

然后，基于以下步骤进行T轮迭代：1)(行③～⑤)并行下发全局模型参数至各客户端，客户端本地运行DP-GRU算法进行模型训练，并上传模型参数更新.2)(行⑥～⑦)服务器对收到的模型参数更新进行加权平均聚合，与上一轮全局模型参数相加，得到下一轮全局模型参数.

T轮循环后，(行⑨)服务器得到最终的全局模型参数ωT，训练结束.在保证数据隐私的前提下，各客户端在本地完成了流量预测任务.

3 实 验

本文在实际交通流量数据集上进行对比实验.先对比了集中式训练与普通联邦学习训练的实验结果；再添加了差分隐私保护模块，分别通过设置不同的ε和不同的客户端数量来测试效果.最终得到一组参数达到较好的预测效果，实现了隐私性与可用性之间的一个平衡，体现了本文方法的优越性与可行性.

3.1 数据集

本文从数据库PeMS中收集实际数据.PeMS是美国加利福尼亚州高速公路的实时车流量数据，由铺设在道路上的检测线圈采集.检测设备每30 s实时收集1次，再每隔5 min聚合1次，形成了最终数据.本文选取PeMS第4区的数据集PeMSD4，即旧金山湾区的交通数据进行实验，此数据集也被其他很多研究者使用[4,17].PeMSD4中有307个传感器，时间跨度为2018年1—2月.交通数据每5 min汇总1次，即每个传感器每天包含288个数据点，每个数据点特征为3种交通测量，即总流量、平均速度和平均占用率.

本文采取如下数据集分割：首先给每个客户端分配相同数量传感器的采集流量数据；然后选取前3周的流量数据作为训练数据集，第4周的流量数据作为测试数据集.

3.2 实验设置

在以往的研究中[4]，GRU是被广泛采用的基线模型，具有很好的交通流量预测性能.因此，本文选取的深度学习模型为基于Pytorch实现的GRU.设定隐藏层层数为1，隐藏层单元数为32，全连接层采用LeakyReLU作为激活函数.学习率为0.001，优化器为SGD算法，损失熵函数为交叉熵损失函数CrossEntropyLoss().经过反复试验，最终选取历史时间步长(timestep)为12.本文全局模型旨在达到这样的目的：针对该区域内的任何传感器，输入过去1 h的流量时间序列，可预测出未来5 min内的流量.

本文采用均方根误差(RMSE)和平均绝对误差(MAE)来表达预测准确性，如式(5)和式(6)所示：

(5)

(6)

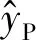
3.3 实验结果与分析

3.3.1 集中式训练与联邦学习训练

本实验对比集中式训练与普通联邦学习训练的效果.集中式训练即将所有客户端的数据集中起来进行训练，普通联邦学习训练即在客户端本地进行训练.设置本地迭代次数E=4，客户端数目m=10，抽样率q=0.5%，学习率η=0.001.相较于本文提出的方法，这2种训练场景均省去了梯度裁剪和噪声添加这2步.

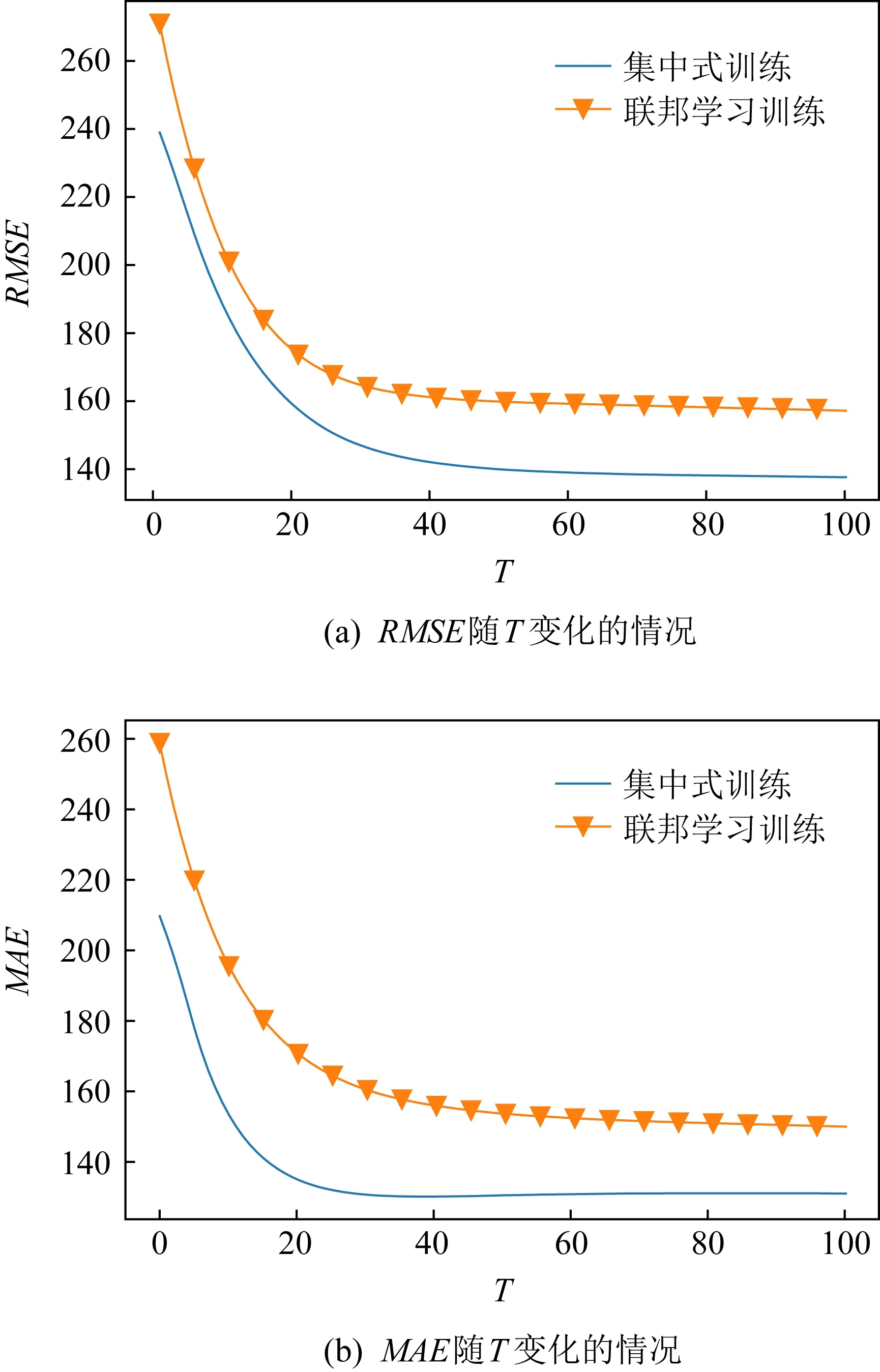
图2 集中式训练与联邦学习训练

图2给出了2种训练场景下，RMSE和MAE随全局迭代次数(T)变化的情况.从图2可以看出，集中式训练与联邦学习训练效果相差无几.这是因为在联邦学习训练场景下，预测的核心技术依然是GRU结构.但联邦学习训练可以通过将训练数据集保留在本地来保护数据隐私，且联邦学习训练模型具有良好的收敛性和稳定性.因此，联邦学习训练可以在保护隐私的前提下实现准确及时的流量预测.

3.3.2 差分隐私对模型准确性的影响

本实验测试在联邦学习训练场景下，添加差分隐私保护模块后，在不同ε下的流量预测效果.参数设置与3.3.1节一致，并设置梯度裁剪阈值C=3.图3给出了当ε分别为2.0，4.0，8.0和10.0，δ=1e-5时，RMSE和MAE随全局迭代次数(T)变化的情况.

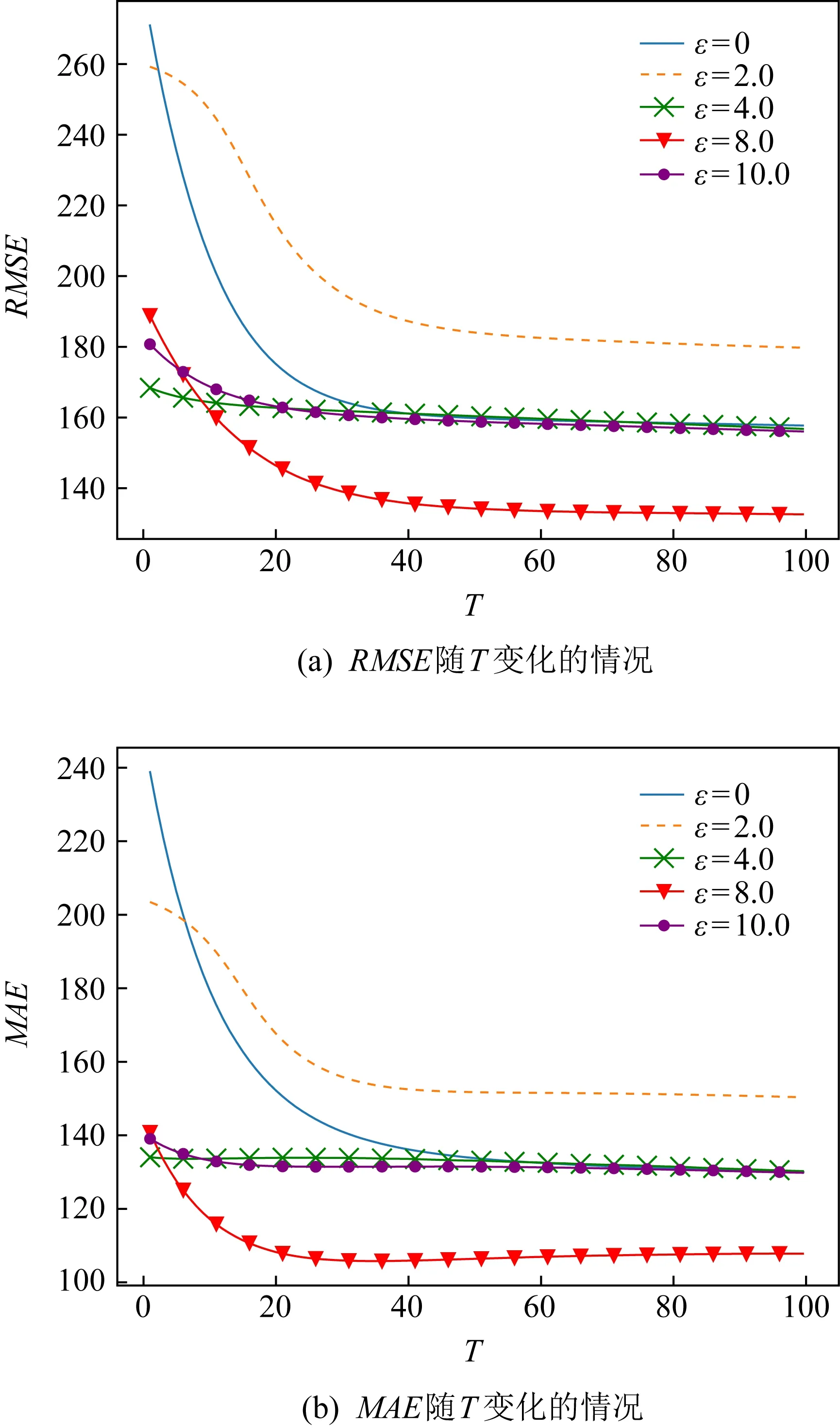
图3 不同ε下的流量预测结果

从图3可以看出，在不同ε下，随着T的增加，2种模型预测误差均逐渐下降，在训练过程中趋于收敛，并最后稳定在一个范围内.从图3也可以看出，ε越小，模型预测误差越大，说明模型训练准确性受影响程度较大；ε越大，模型预测误差越小，说明模型训练准确性受影响程度较小.可见模型训练效果与ε大小成反比，符合差分隐私理论的设计.根据差分隐私理论，ε越小，添加噪声越大，算法隐私保护效果越好；ε越大，添加噪声越小，算法隐私保护效果越差.从实验结果可以得出，当ε=2.0时，模型预测误差较高，即添加噪声过大，应当舍弃此参数.当ε=4.0，8.0和10.0时，预测效果与普通联邦学习训练效果(ε=0时)趋于一致，且最后均收敛到了稳定区间，说明差分隐私并不影响模型的收敛性.从实验可以得出，当m=10,ε=4.0时可以在模型隐私性和可用性之间取得一个平衡.

3.3.3 客户端数量对模型准确性的影响

在交通预测场景中，不排除多个机构协同进行训练的情况.例如，文献[7]考虑到了有多个参与者的大规模场景，设计了一个联合协议，通过以一定比例抽取参与者的方式减轻了通信负担.但文献[7]仅仅只是普通联邦学习训练，其安全性还有待提升.本文在3.3.2节得到的ε=4.0的基础上分别设置不同的客户端数量，观察全局模型预测效果与客户端数量的关系.

图4给出了当客户端数量m为5，10，15，20，25时，RMSE和MAE随全局迭代次数(T)变化的情况.

图4 不同客户端数量下的流量预测结果

从图4可以看出，在不同客户端数量下，一开始全局模型的训练效果可能会有差异，但最后均收敛至一定区间，说明框架具有良好的收敛性，不会随客户端数量发生改变，适用于不同规模下的联合预测场景.由实验结果可得，在ε=4.0的条件下，当m=20时，模型预测结果达到了最佳.

4 结束语

本文提出一种面向交通流量预测隐私保护的联邦学习方法.基于差分隐私的随机性性质，在客户端采用差分隐私随机梯度下降算法，不仅使得客户端在本地训练，也防止攻击者从模型共享梯度中逆推出原始数据，从而达到保护数据隐私的目的.本文首次将差分隐私随机梯度下降应用于GRU循环神经网络，可供其他研究者借鉴.本文方法可在模型可用性和隐私性之间取得一个较好的平衡，并可推广到不同规模的应用场景.考虑实际场景应用现状，根据每个机构的安全级别，采用混合差分隐私机制以更有效地提高预测效果是接下来的研究目标.