基于深度学习的新能源汽车充电路径规划模型

郑 振 唐 菲

（1.武汉软件工程职业学院，湖北 武汉 430205；2.武汉船舶职业技术学院，湖北 武汉 430000）

0 引言

与传统的内燃机汽车相比，新能源汽车效率更高，许多国家都制定了相关政策来促进新能源汽车的发展。新能源汽车需要频繁充电，因此汽车的充电路径调度和规划系统必不可少。如何让充电过程更加便捷成为研究的重点。有研究者提出充电桩规划方法，例如Cui Qiushi等人建立了混合整数非线性的多目标优化模型，以降低充电站、配电网扩建等联合成本。Zhang Ying等人提出了一种面向多标准的充电设施部署方法，设计了具有性能保证的充电站放置加速算法。有研究着重分析了充电桩的比例及其使用情况，提出了算法来估算停车充电需求。然而，多数研究并没有对充电的路径进行规划。新能源汽车的位置会随着时间发生变化，其充电的需求具有时空特性。新能源汽车在慢速充电模式下，汽车需要很长时间才能充满电，会产生较长的停车时间。在进行路径规划时，需要考虑汽车的剩余电量是否能支持汽车达到充电站。该文研究新能源汽车充电路径规划，以减少总充电时间和为了充电所花费的额外距离作为目标。结合深度学习算法，提出了新能源汽车充电路径规划模型，为用户规划新能源汽车充电路线。

1 优化模型

新能源汽车充电路径规划问题的目标是将汽车调度到合适的充电桩进行充电，以使总的充电时间最小化，并最大限度地缩短新能源汽车从起点到目的地的距离。新能源汽车在充电上花费的总时间包括到充电站的行程时间、排队时间和实际充电时间。这个问题的解决方案可以简化为寻找最近的快速充电桩，而忽略电动汽车的排队时间。如果只考虑电动汽车的排队时间，策略是选择具有较少等待充电车辆的充电站。在现实世界中，电动汽车充电调度问题有以下约束：每辆电动汽车只能选择一个充电桩进行充电，直到其电池达到上界E；电池中剩余的电量使电动汽车无法到达某些充电站；充电站的快充桩m 、慢充m 的数量和充电速率有限，导致实际的电池充电时间较长。为了减少在有限数量的充电站充电所花费的总时间，为汽车设计最优和高效的充电策略更重要。新能源汽车的充电需求具有时空特性。在实际应用中，新能源汽车的充电模式可分为慢速充电和快速充电。在慢速充电模式下，汽车产生较长的停车时间。此外，在进行路径规划时，需要考虑汽车的剩余电量是否能支持汽车达到充电站。结合上述约束，新能源汽车充电路径规划问题的表述如公式（1）所示。

充电路径规划的流程如图1所示。其中，充电能耗模型模块计算每辆新能源汽车的行驶用电量，该模块获取汽车的参数，如初始电池电量、到充电站的距离，并输出EV的耗电量；数据预处理模块以能耗模型、路网数据和充电站数据的结果作为输入，对原始数据进行预处理，并使用地图匹配将每个汽车的GPS点映射到相应的路段上；汽车和充电站图模块用于建立汽车和充电站的分布图，将用于为汽车充电调度系统构建仿真环境；路径规划模块是基于深度Q学习的学习模型，为所有需要充电的汽车推荐最优调度决策。

图1 充电路径规划的流程

2 路径规划算法

由于汽车电池的初始剩余电量会影响其充电时间和可用行驶距离，因此使用汽车行驶的距离来预测相应的用电量。通过对实际数据的分析可知，汽车的行驶距离与电池电量消耗之间具有近似线性关系。该文使用线性回归模型来预测汽车用电量，如公即式（2）所示。

其中，、如公式（3）、公式（4）所示。

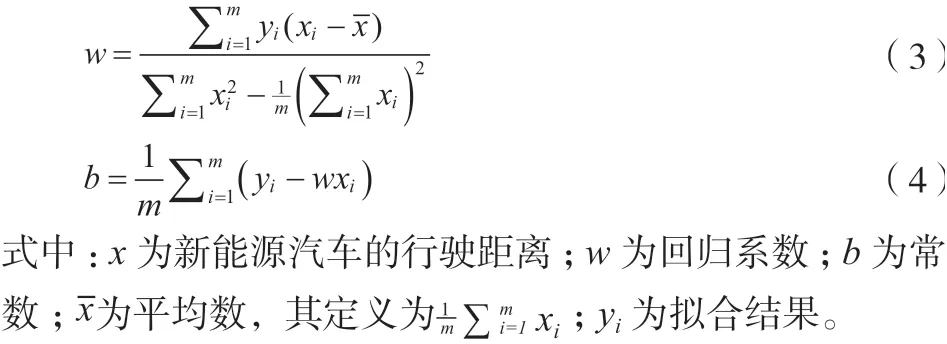
充电路径规划问题是一个顺序决策问题，其目的是最大限度地减少充电所花费的总时间，并减少行驶距离。

使用元组，，，，来表示马尔可夫过程，其中为状态集合，为动作集合，为从状态S到状态S的转移概率，（，）为奖励函数，为折扣因子。

汽车充电调度系统可以定义为一个代理，它通过对所有需要充电的电动汽车的充电站选择和充电路径做出一系列决策来完成所有电动汽车的充电。使用马尔可夫过程模型对汽车充电调度过程进行建模。

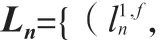
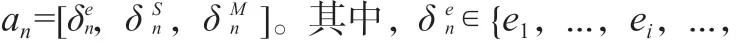
奖励反映了通过执行从状态s开始并导致下一个状态s的动作观察到的特定状态转换的可取性。

奖励信号是强化学习目标的形式化表现。在训练学习的每步中，奖励是一个实数值信号。学习目标就是奖励的最大化，但是这个最大化的目标不一定是即时奖励（即每步行动后环境反馈给智能体的奖励），而是从长期角度来看的累计的总体奖励。用总体奖励来作为学习目标的形式化描述是强化学习的区别于其他人工智能学习类型的一个最独特的特征。路径规划的目标是最大限度地减少所有汽车充电所花费的总时间，并最大限度地缩短汽车的起点和目的地之间的距离。因此，奖励函数就具有的形式如公式（5）所示。

充电任务的最佳调度需要确定一个固定策略，该策略定义了在步骤t所使用的调度动作a。学习汽车调度任务的目标是找到一个最优策略，以最大化调度奖励的总和。最优策略的计算如公见式（6）所示。

将最优动作值函数Q（s，a）定义为智能体状态为s并采取最优动作a时的最大预期回报，其定义如公式（7）所示。

使用深度Q网络（DQN）对汽车的充电路径规划进行建模。在DQN模型中，近似的动作价值函数为（s，a；），其中（s，a；）≈Q（s，a）。在学习过程中，Q网络通过在每次迭代时最小化损失函数L（θ），并且可以被训练来学习动作值函数的参数。损失函数L（θ）的定义如公式（8）所示。

式中：θ为第次更新时神经网络的参数。对迭代时神经网络参数的损失函数进行微分，得到公式（9）。

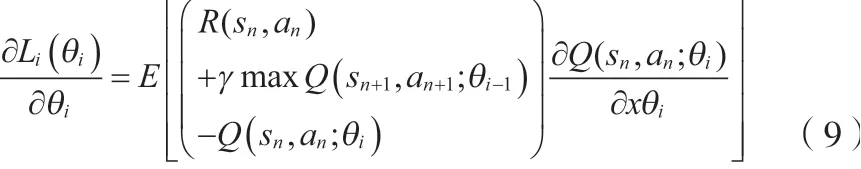
该模型使用随机梯度下降方法来优化损失函数。为了平衡exploration和exploitation的过程，该模型学习了最优动作a，同时选择了随机动作来确保对状态空间的充分探索。即智能体以1-的概率选择当前的最优动作，并以的概率选择一个随机动作。

3 试验评估

该节进行了有效的试验来评估上述系统。首先描述使用的数据集，其次展示试验结果。试验从Open Street Map（OSM）收集道路网络数据，汽车充电站数据来自高德地图。OSM是一个网上地图协作计划，是由网络大众共同打造的免费开源、可编辑的地图服务，其目标是创造一个内容自由且能让所有人编辑的世界地图。每个充电站数据包括充电站ID、充电站位置、充电站经纬度坐标（GPS点）、快充桩和慢充桩数量。

随机生成汽车的GPS坐标数据，将GPS点映射到道路网络中的相应路段。选择汽车一定范围内的兴趣点（如学校、银行、饭店、医院）作为目的地。汽车的行驶距离是根据OSM路网中汽车与充电站之间的最短导航距离计算得出。为了评估电动汽车的排队时间，采用到达充电站的充电桩数量和当前到达电动汽车的充电时间来估计。

试验部分评估了充电路径规划模型的有效性。汽车的平均速度为55 km/h，电池的充电上限为900 Ah，下限为200 Ah。深度Q学习的神经网络由4个密集连接层组成，每个连接层的神经元数量分别为100个、1024个、512个和4个。激活函数是整流线性单元，用于训练的优化器是Adam，学习率为0.0001。

不同参数设置下汽车起点到目的点距离减小的概率密度函数如图2所示。对=1、=10，距离减少量小于0的概率远低于=10、=1的情况。其中，距离减少量为负，表明选择的充电站距离汽车的初始目的地较远。当减少量更接近1时，选择的充电站更接近汽车的初始目的地。由于受每辆汽车初始剩余电量的影响，电动汽车可以到达的充电站选择有限。因此，算法对行驶距离的优化是有限的，但调整参数和可以使充电策略在有限的选择中更倾向于选择更接近电动汽车目的地的充电站。

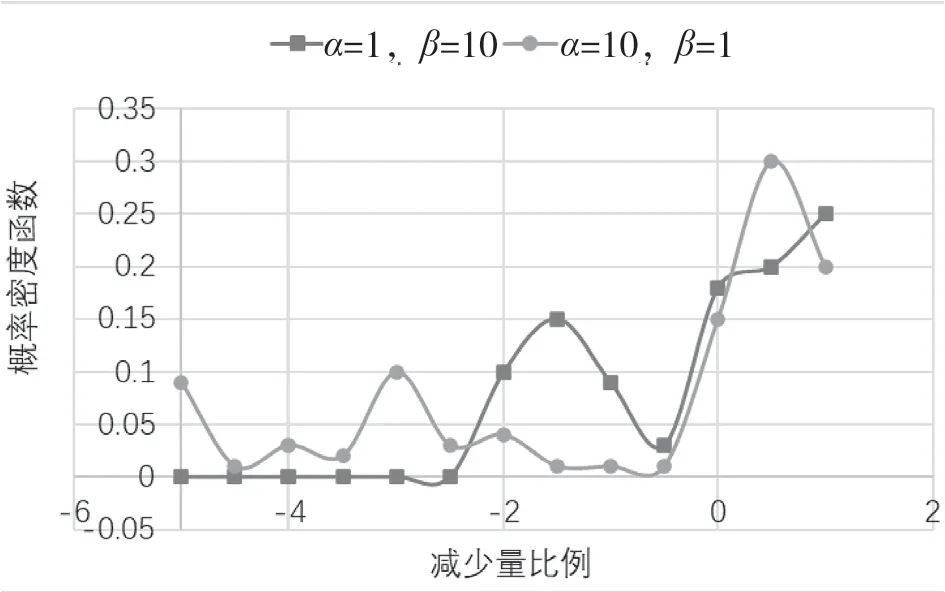
图2 距离减少量的概率密度函数

将该文提出的方法与最近邻基线算法进行比较。最近邻算法将每辆汽车安排到离它最近的充电站，然后根据到达时间选择该站的充电桩，使其最早开始充电。汽车完成充电时间的累计分布函数如图3所示。由结果可知，最近邻算法的完成充电时间比该文算法长。对该文算法，超过90%的汽车能够在4 h内完成充电。对最近邻算法，大约20%的汽车充电时间超过了4 h。由于最近邻算法只考虑距离当前充电电动汽车最近的充电站（即最快到达的充电站），而没有考虑充电站的充电桩数量和不同充电桩的充电率，所以电动汽车的完成充电时间比该文算法长。

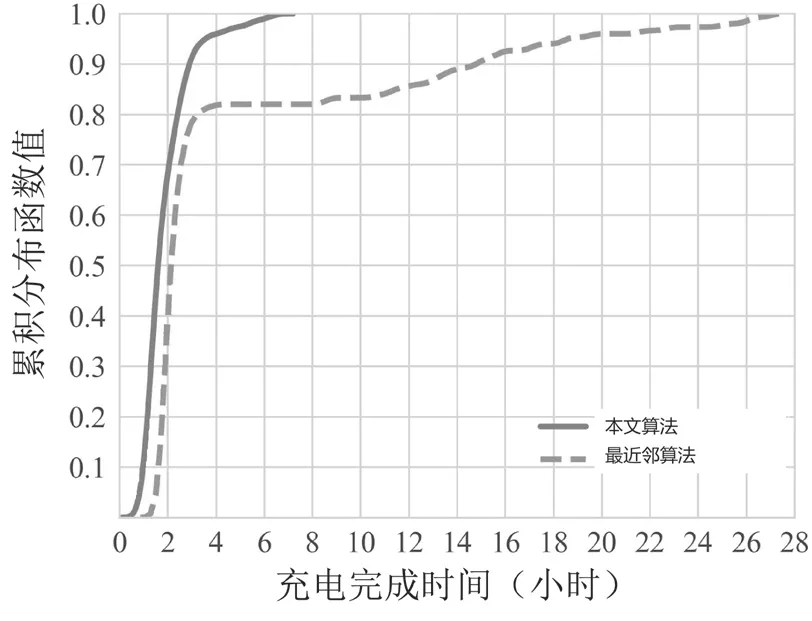
图3 完成充电时间的累计分布函数

4 结论

该文提出了基于深度学习的充电路径规划模型，对新能源汽车充电进行调度。使用真实数据集试验，结果表明该文所提出的模型减少了充电时间，缩短了车辆的行驶距离。该模型从新能源汽车用户的角度考虑约束，即汽车的行驶距离限制、不同的充电模型以及充电请求的空间特征。在后续的研究工作，将计划利用实时交通和充电站状态数据来进一步改进该文模型。