乒乓球技战术能力分析中的代理模型方法研究

李佳，朱李华

(大连交通大学 体育工作部，辽宁 大连 116028)

乒乓球运动中，技战术能力是运动员竞技能力的核心要素，因此，技战术能力成为乒乓球运动科学研究的热点.相应地，一些统计分析相关的数学工具或方法被引入到该领域的研究当中.如吴飞等[1]将Logistic 回归模型运用于乒乓球的技战术分析中，对技战术进行推断型的统计分析.徐君伟等[2]利用SPSS17.0软件，对几次赛事的技战术能力指标进行Pearson 相关分析.赵喜迎等[3]为了评估比赛质量，对比赛采用了文献资料法、录像观察法和逼近理想解的排序法(TOPSIS).杨青等[4]利用BP神经网络和多元回归方法针对世界排名前20位(2012-2014年)男子进攻型选手的62场比赛进行了技战术分析，得出了一些有价值的结论.李菊[5]提出了基于波士顿矩阵分析模型的乒乓球技战术效益分析方法.

如今，乒乓球运动已在各大高校如火如荼地开展起来，该运动一方面增强了学生的体质，锻炼了学生的意志品质，另一方面对大学生爱国情怀的培养具有积极的意义.为了更好地对比赛进行总结分析，进而能够提出科学的指导意见，近年来加强了对比赛过程的统计整理工作.本文拟在整理比赛数据的基础上，针对高校学生运动员的个体，在“四段指标评估法”[6]的框架下，利用代理模型方法，研究高校乒乓球运动员的技战术能力的运用和执行情况，发现问题并找到不足，为今后实施针对性的训练提供一定的理论依据和参考.

1 乒乓球比赛得分情况的分析与归纳

以本校某特长生为例.选取一年来该学生参加的10余场比赛中的41局进行分析.利用文献[6]的得失分分类方法以及分类代码，以第一场比赛第一局作为示例，如表1所示.

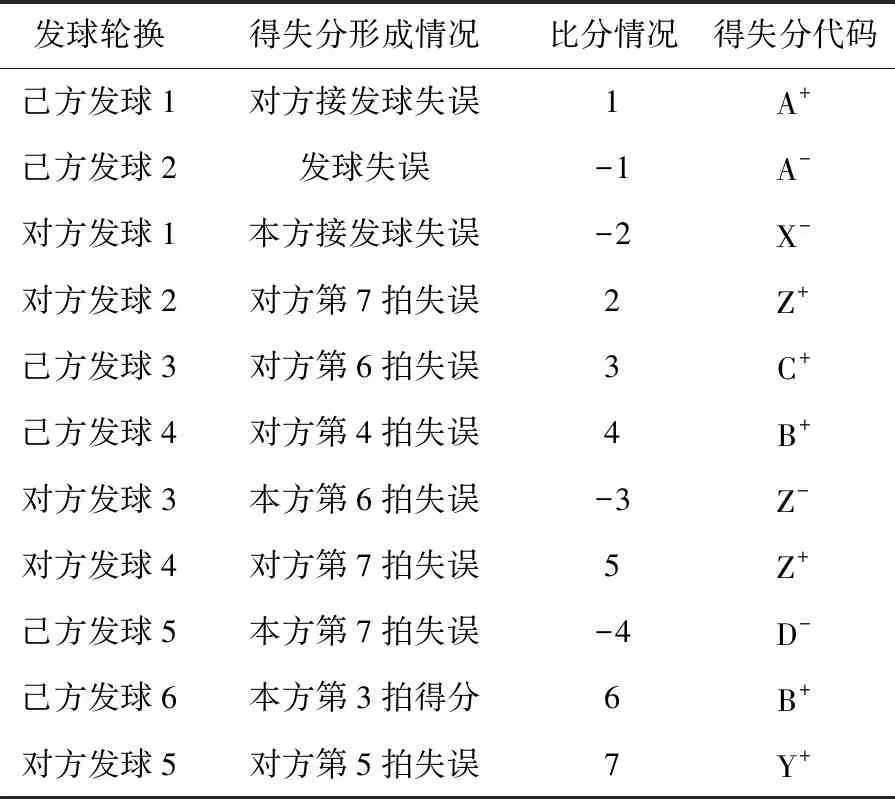
表1 得失分情况统计

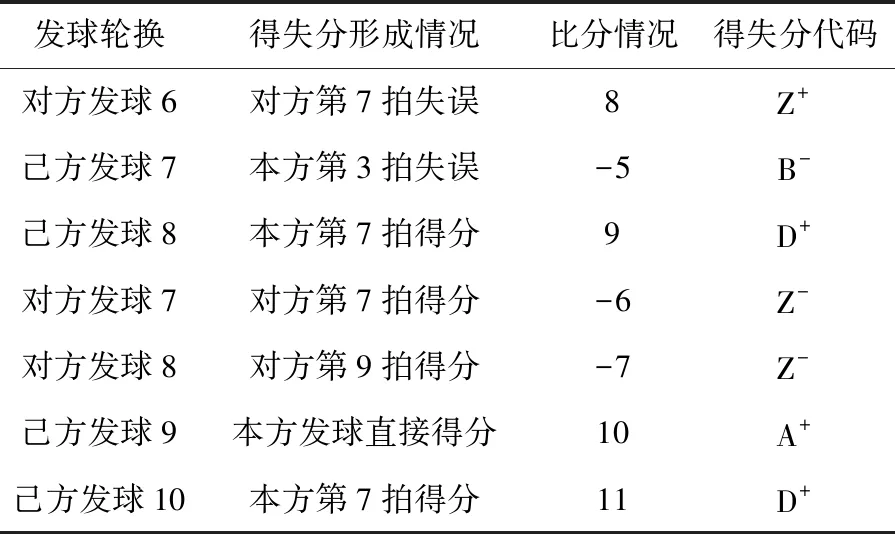
表1 得失分情况统计 续表

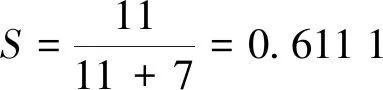
发抢得分率为：

接抢得分率为：

发球相持得分率为：

接发球相持得分率为：

依此类推，可将该同学的41局比赛的局得分率、发抢得分率、接抢得分率、发球相持得分率、接发球相持得分率，计算结果列于表2所示.

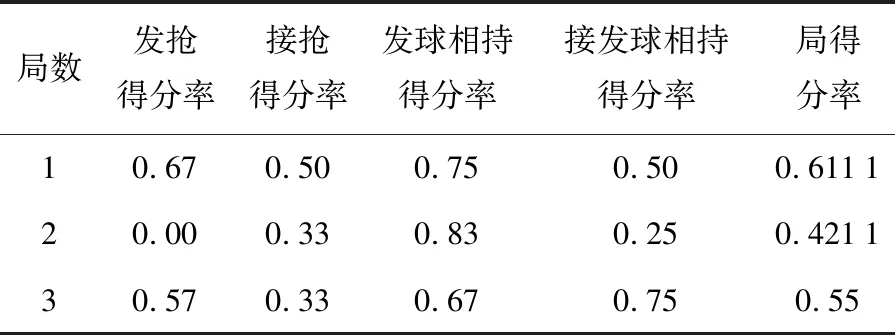
表2 能力指标的计算

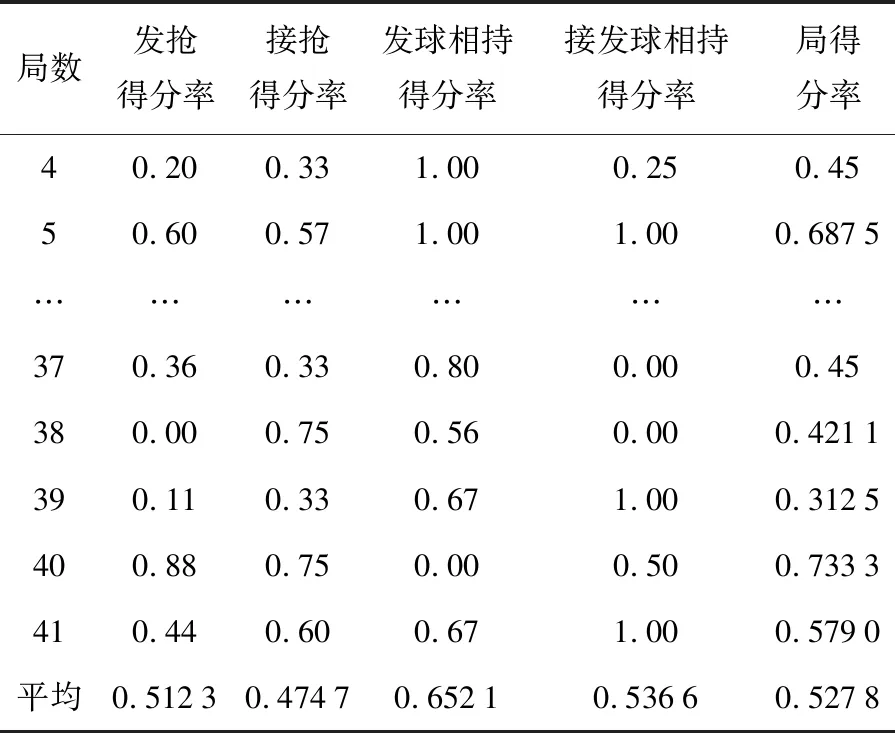
表2 能力指标的计算 续表

2 技战术能力模型的建立

代理模型是指为降低模型复杂度，减小计算量而构建的与真实模型相近似的分析模型[7].常见的代理模型中，径向基函数代理模型具有结构简单、计算量少、灵活性好、预测精度高等特点，目前已在各个领域得到了较广泛的应用[8-10].

本文采用径向基函数代理模型，建立四项能力指标与局得分率之间的函数关系.模型的基本形式如下：

(1)

式中:n为采样点个数；ri=‖X-Xi‖为欧氏距离；α、β为形参数；wi为线性叠加系数.自变量X=(x1,x2,x3,x4)为四维矢量；Xi=(x1i,x2i,x3i,x4i)为采样点；则

(2)

(3)

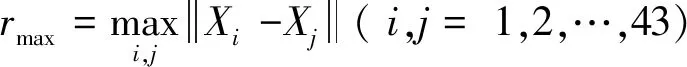
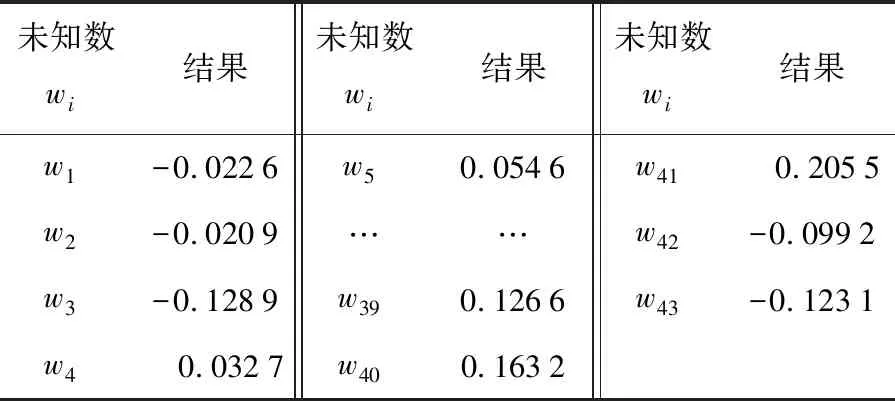
表3 计算结果(部分)

将43个系数代入式(1)，则可建立四项能力指标与局得分率之间的关系.

3 模型精度的检验分析

本质上，径向基函数代理模型是一种插值模型，样本点处误差为零，因而代理模型的精度，需要通过样本点之外的测试点来检验评价.为此，另取一组非采样点的比赛数据作为测试点，检验一下模型的精度，数据见表4.

表4 测试数据及结果

由表中可知，最大误差为第二局，相对误差为3.54%，相当于28分里面出现1分的误差，因而模型的精度是比较高的.

由表2可知，该同学的四项能力指标平均值为x1=0.512 3，x2=0.474 7，x3=0.652 1，x4=0.536 6，可以看出，其中第三项即发球相持得分率数值最大，接发球相持得分率次之，而接抢得分率最低.表明该同学比赛中的相持能力相对较强，而比赛抢攻能力稍弱.

尽管实际比赛中的四项能力指标是离散量，不可能是连续变化的，但不妨碍将其假设为连续量，采用求导数的方法来分析其变化对结果的影响.对式(1)自变量X的分量xj(j=1,2,3,4)求偏导数，有

(4)

将平均能力指标x1=0.512 3，x2=0.474 7，x3=0.652 1，x4=0.536 6代入，可得

从数据可以看出，该学生运动员在发挥平均水平发挥的情况下，四项能力指标中，发抢得分率的变化对局得分率的影响最大，接抢得分率变化的影响处于第二位置，接发球相持得分率的变化对局得分率的影响排在第三位，而发球相持得分率尽管数值最大，但其变化对局得分率的影响反倒是最小的.从上述分析可知，该同学应重点提高自己的抢攻能力，尤其是发球抢攻能力，相比其他三项能力可以更容易地提高局得分率.同样，提高自己的接发球抢攻能力也可以较有效地提高局得分率.

众所周知，乒乓球比赛中，发球一方往往具有更大的得分优势，因而为了获得比赛的胜利，发抢得分率和发球相持得分率最好不低于0.5.保守的，以0.5为例，即x1=0.5，x3=0.5，令接抢得分率取定值，如x2=0.2，再令接发球相持得分率x4由低(0.1)到高(1.0)变化，可以根据式(1)绘制曲线，如图1中的曲线1.同样的，可以得到接抢得分率取其他值时的关系曲线，如图中的曲线2～曲线8所示.即图中曲线1～8分别对应接抢得分率x2=0.2～0.9，该图设置条件为：发抢得分率和发球相持得分率均为0.5，一局比赛若取得胜利，显然局得分率要大于0.5，一局比赛若取得胜利，显然局得分率要大于0.5，由图中可知，在x1=0.5，x3=0.5的假定条件下，若接抢得分率很低，如曲线1所示，接发球相持得分率再高也无法获得胜利，而随着接抢得分率的提高，获胜的概率随之提高，即图1中局得分率为0.5的横线以上部分所占比例越来越大.当接抢得分率超过0.9时，即便接发球相持得分率接近0，也几乎可以获得胜利.

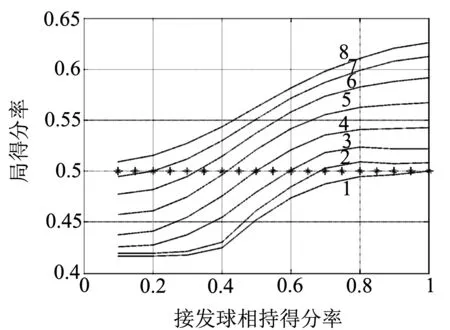
图1 接发球相持得分率与局得分率的关系曲线

4 结论

(1)论文针对某大学生运动员的41局比赛进行了能力指标的分析和整理.可以发现该同学发球相持得分率数值最大，接发球相持得分率次之，而接抢得分率最低.表明该同学比赛中的相持能力相对较强，而比赛抢攻能力稍弱;

(2)利用径向基函数的代理模型方法构建了发抢得分率、接抢得分率、发球相持得分率、接发球相持得分率四项能力指标与局得分率之间的数学模型，精度验证可知该模型最大相对误差为3.54%，表明模型具有较高的精度;

(3)通过模型可以得知，该大学生运动员应该重点加强发球以及接发球抢攻能力方面的训练，提高发抢得分率以及接抢得分率,可以更有效地提高局得分率.同时，利用该模型可以针对某些条件下的比赛获胜概率进行一定的预测，如在假定己方发球环节的两项能力指标处于0.5的水平的条件下，接抢得分率超过0.9时，几乎可以获得该局比赛的胜利.