一种基于工具坐标系的机器人运动学参数标定方法

高文斌 褚亚杰 余晓流

1.安徽工业大学机械工程学院，马鞍山，243032 2.特种重载机器人安徽省重点实验室，马鞍山，243032

0 引言

定位精度是评价机器人性能的重要指标，包括重复定位精度和绝对定位精度。工业机器人具有良好的重复定位精度，可达0.01 mm，但受零部件加工、装配及使用磨损等产生几何参数误差的影响，绝对定位精度较低[1-3]。参数标定是提高机器人绝对定位精度的一种经济有效的方法[4-5]。

D-H(Denavit-Hartenberg)参数法和指数积公式是串联机器人参数标定常用的数学工具。D-H参数法需要的参数量最少，但相邻关节轴线平行或接近平行时，机器人会出现奇异性问题[6]。一些学者通过增加参数解决奇异性问题，但如此也带来了模型推导不直接、形式复杂等新问题[7-10]。针对上述问题，一些学者基于指数积公式开展了运动学参数标定的相关研究，当相邻关节轴线平行或接近平行时，指数积形式的运动学模型相对关节运动是光滑变化的，不会出现奇异性问题[11-13]。目前，机器人误差模型大多以基础坐标系为参考系，坐标系的转换导致误差模型中包含姿态误差与位置矢量的乘积项，影响了参数标定识别精度。以工具坐标系为参考系建立误差模型，避免了姿态误差与位置矢量的乘积项对参数标定识别精度的影响[14]。本文以工具坐标系为参考系，给出一种基于指数积公式的包含关节约束条件的位姿误差标定模型。采用激光跟踪仪作为测量设备，通过对UR5机器人进行位姿标定试验，验证标定模型的正确性和有效性。

1 误差模型的建立

如图1所示，机器人由n个单自由度关节串联而成。分别在基座和末端执行器上建立基础坐标系{B}和工具坐标系{T}，n自由度串联机器人运动学模型为[11]

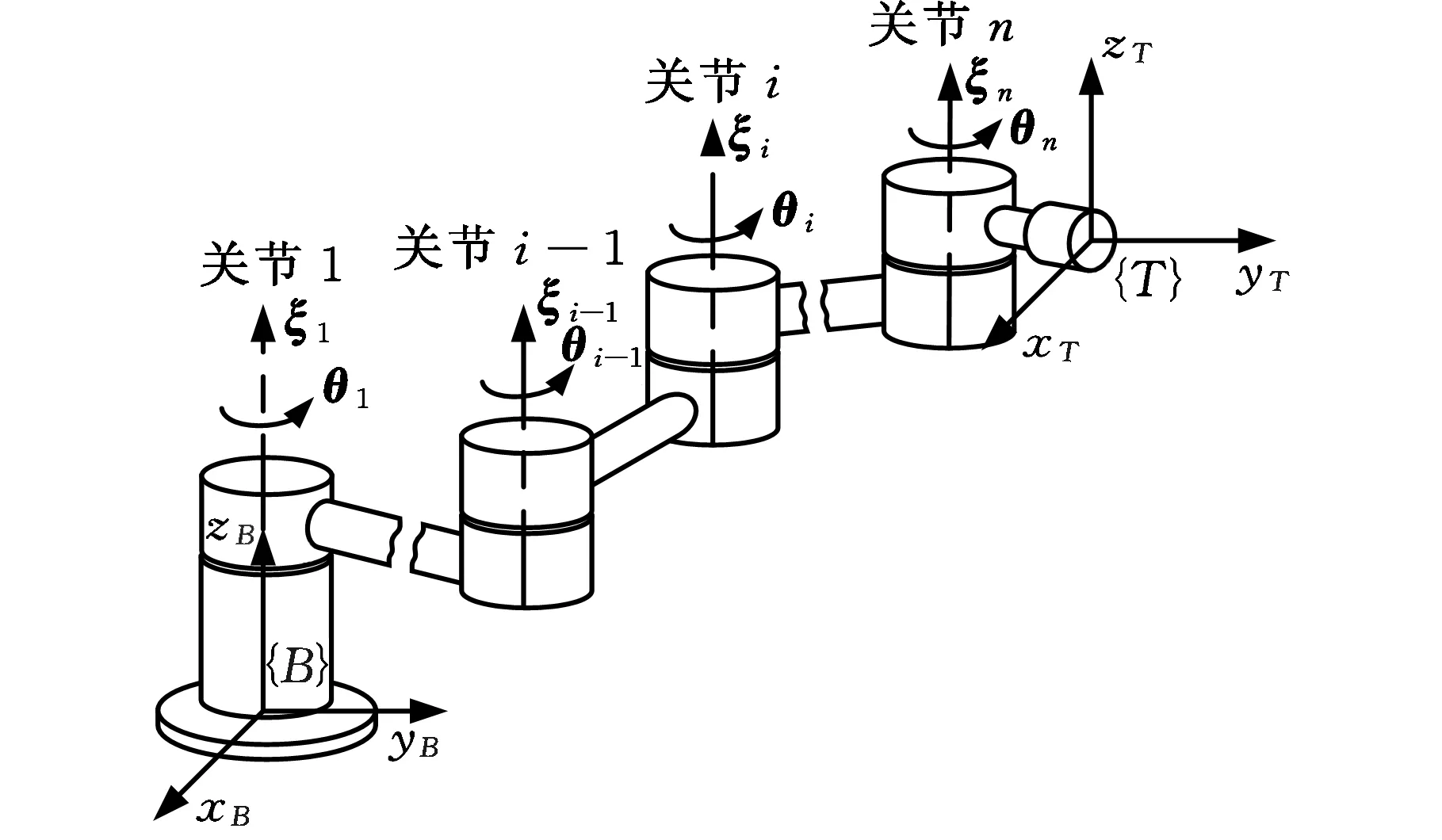
图1 n自由度串联机器人Fig.1 n-DOF serial robot

(1)

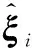
(2)

机器人运动学模型(式(2))可简写为

f=f(ξ,θ,ξst)

(3)

机器人的位姿误差可以通过对运动学模型两边取微分获得：

(4)

(5)

对式(4)右乘f-1得到以基础坐标系为参考系的误差模型δff-1，δff-1为末端执行器相对于基础坐标系的空间速度；对式(4)左乘f-1得到以工具坐标系为参考系的误差模型f-1δf，f-1δf为末端执行器相对工具坐标系的物体速度。根据式(5)，两种误差模型可分别表示为[14-15]

(6)

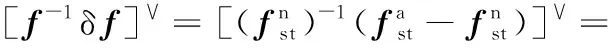
(7)

式中，Rn为理论姿态；pn为理论位置；Ra为实际姿态；I4为4×4的单位矩阵；pa为实际位置；运算符“∨”表示李群SE(3)到李代数se(3)的映射。

实际姿态Ra和实际位置pa可通过测量获得。

以基础坐标系为参考系建立误差模型时，末端执行器位姿误差表示在基础坐标系中，式(6)中pa-Ra(Rn)Tpn除了受实际位置pa的影响外，还引入了实际姿态Ra的影响；以工具坐标系为参考系建立误差模型时，末端执行器位姿误差表示在工具坐标系中不需要进行坐标系转换，式(7)中(Rn)T(pa-pn)只受实际位置pa的影响。本文以工具坐标系为参考系，建立误差模型为

(8)

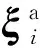
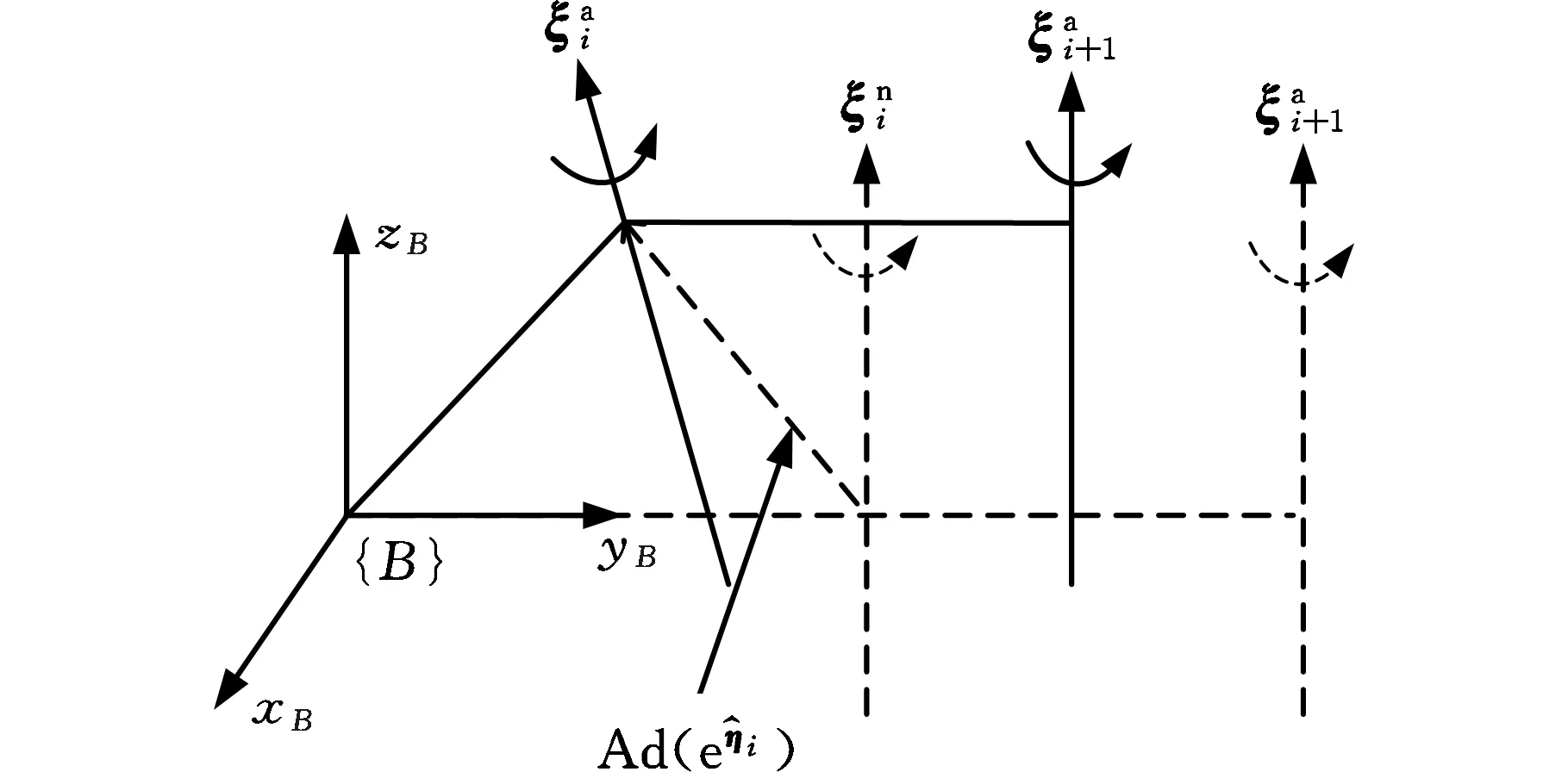
图2 关节旋量误差Fig.2 Joint twist error

(9)

可知，经伴随变换后，关节旋量坐标仍然满足关节约束条件[16]，即

(10)

(11)

图3 初始位姿误差Fig.3 Initial pose error

(12)

将式(9)、式(12)代入运动学模型(式(2))中，可写为

(13)

机器人的误差模型(式(8))可改写为

(14)

关节的零位偏置误差可以看作是旋量误差的一个误差源，在标定过程中，仅需识别关节旋量误差η和初始位姿误差ηst，式(14)可简化为[16-17]

(15)

2 标定模型的建立

2.1 标定模型线性化

将运动学模型式(13)代入式(15)中，可得

[f-1δf]∨=

(16)

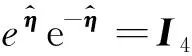
(17)

由恒等式式(17)易知

(18)

Bi=Ad-1(Ai)-I6i=1,2,…,n

利用式(18)可将式(16)化简为

(19)

(20)

(21)

将式(20)、式(21)代入式(19)可得运动学方程线性化模型的显式表达式:

(22)

(23)

运动学方程线性化模型(式(22))可以写成如下矩阵形式：

y=Cx

(24)

C=[C1C2…CnCn+1]∈R6×6(n+1)

C的各列如下：

2.2 参数标定模型

控制串联机器人运动到工作空间中k个标定位姿，得到k组线性化方程，联立可得运动学参数标定方程为

(25)

x可通过最小二乘法求解获得：

(26)

3 试验及结果分析

如图4所示，以UR5机器人为试验对象，其重复定位精度为0.03 mm。以Lecia AT960-MR激光跟踪仪为测量设备，在半径为40 m范围内该设备测量精度为15 μm+6 μm/m。试验时，将机器人放置在激光跟踪仪的工作空间内。

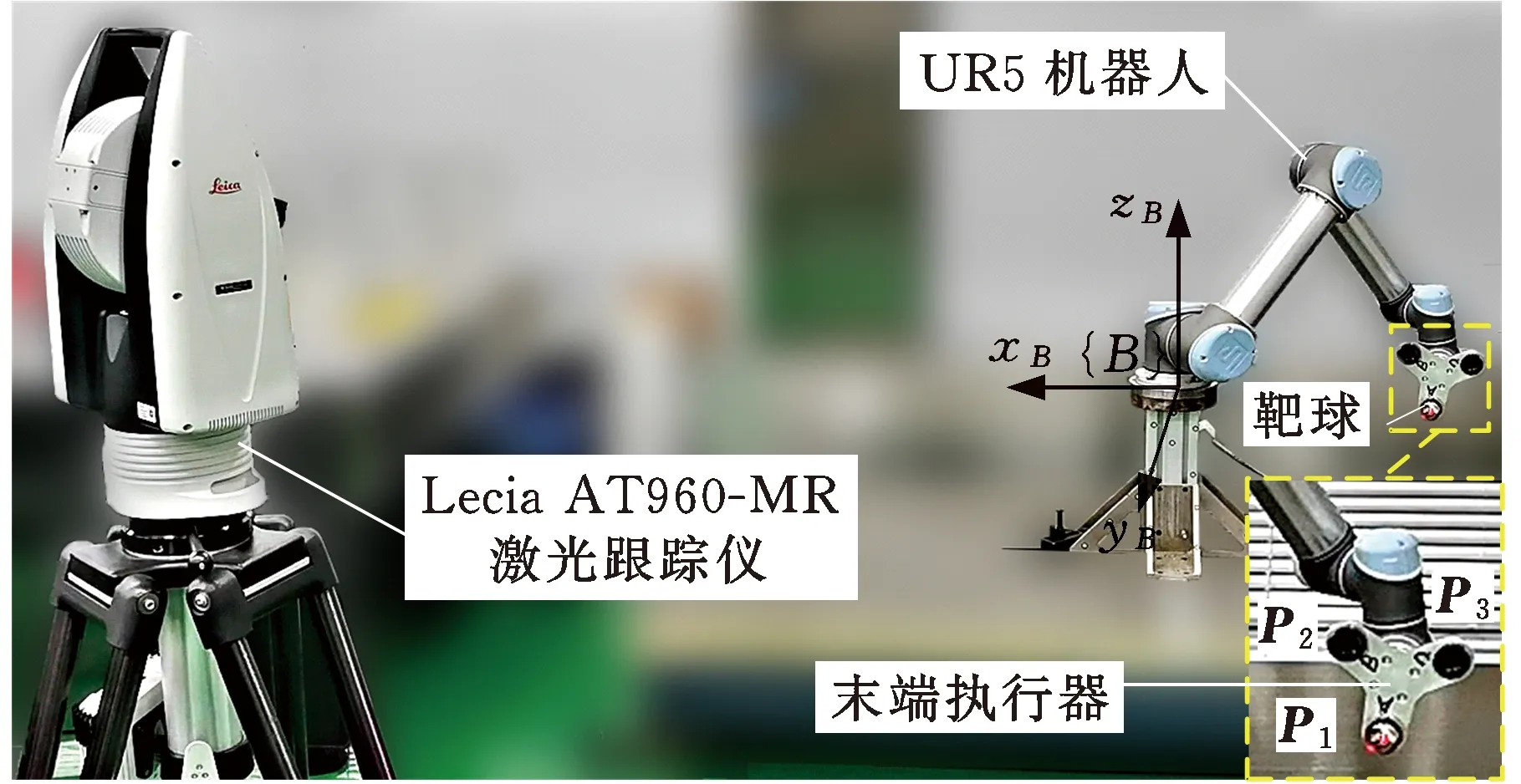
图4 标定试验设备Fig.4 Calibration test equipment

3.1 坐标系建立

通过Spatial Analyzer软件建立机器人基础坐标系{B}，并设置激光跟踪仪坐标系与基础坐标系重合，使靶球坐标表示在基础坐标系中。

如图5所示，测量P1、P2、P3相对于基础坐标系的位置坐标，以点P1为原点建立工具坐标系{T}，xT轴与向量P1P3方向一致，zT轴与三点所在平面的法向量n方向一致，n=P1P3×P1P2，yT轴通过右手定则确定。工具坐标系{T}相对于基础坐标系{B}的测量位姿可表示为

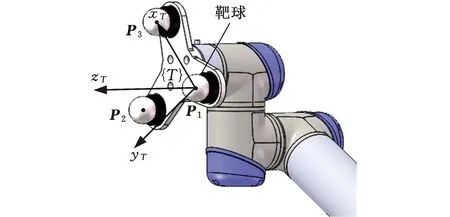
图5 工具坐标系建立Fig.5 Establish the tool frame

(27)

3.2 标定流程

运动学参数标定识别流程如图6所示，控制机器人运动到一系列标定位姿,根据理论运动学模型计算出末端执行器位姿的理论值，通过激光跟踪仪测得末端执行器三个测量点相对于基础坐标系的位置坐标，根据式(27)建立工具坐标系{T}，计算得到末端执行器位姿的测量值。标定模型中误差量xi可通过最小二乘法(式(26))获得。在参数的迭代识别过程中，从k-1步到k步的参数ηi更新方式为

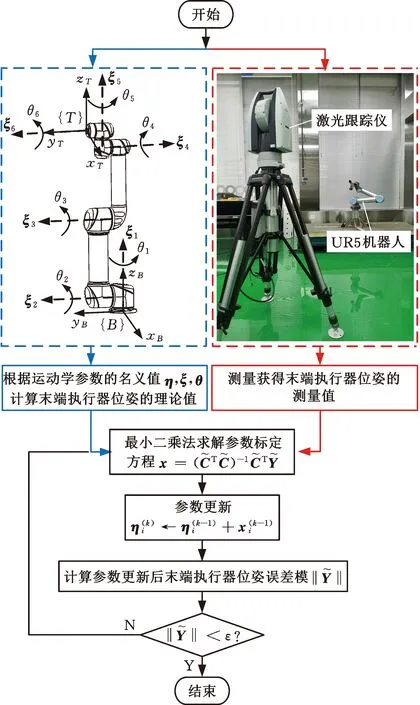
图6 参数迭代标定流程Fig.6 Calibration procedure for parameters identification

(28)

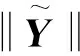
3.3 标定试验

在机器人的工作空间内随机生成30组关节变量，用于运动学参数标定试验。根据关节变量值控制机器人运动到相应位姿，通过激光跟踪仪测得末端执行器三个测量点的位置坐标值，如表1所示，并利用式(27)计算出末端执行器位姿的实际值。按照图6所示的流程进行运动学参数的辨识。如图7所示，位置和姿态误差模在4次迭代后收敛到稳定值。

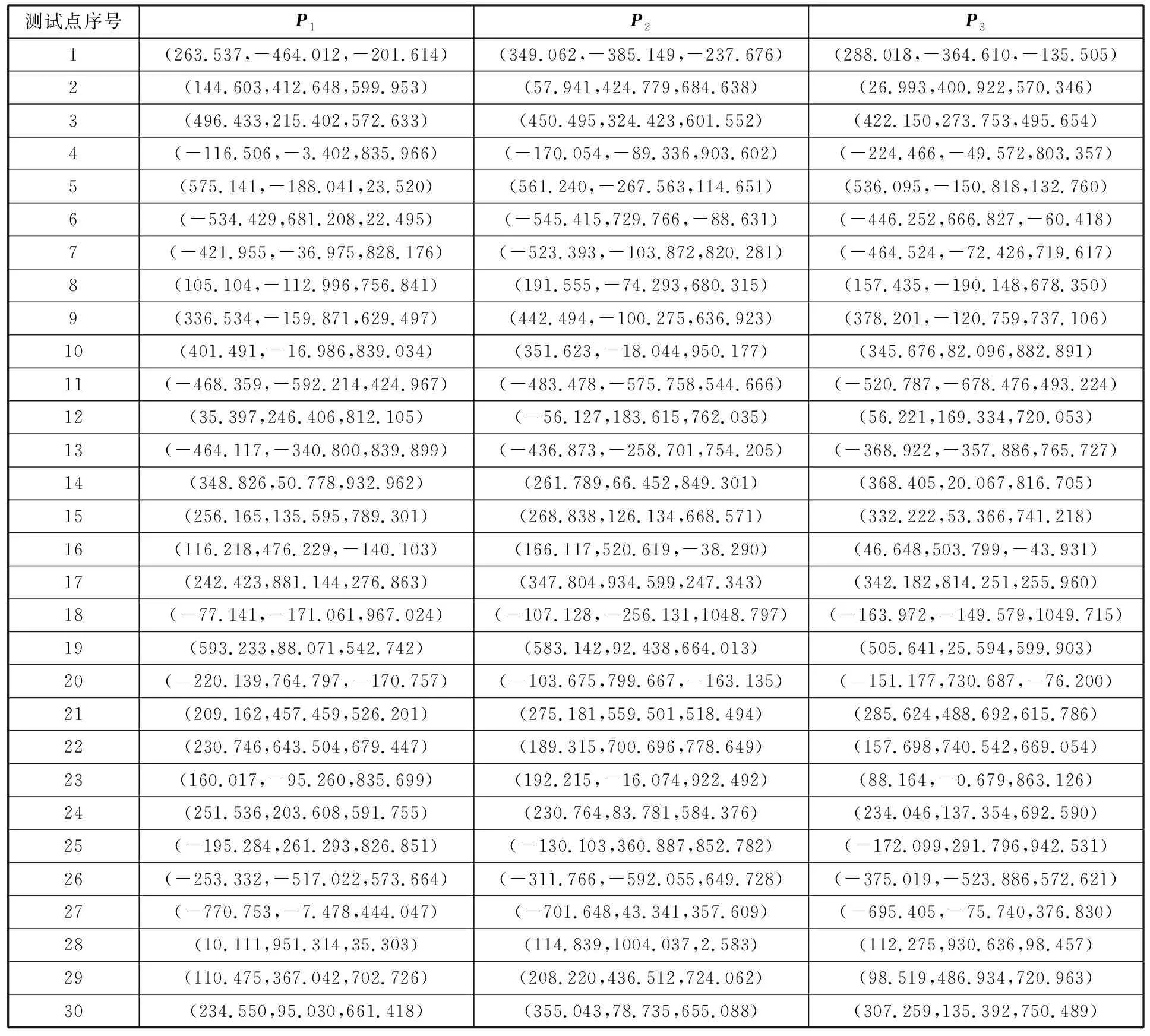
表1 标定试验位置坐标Tab.1 The position coordinates for the calibration test mm

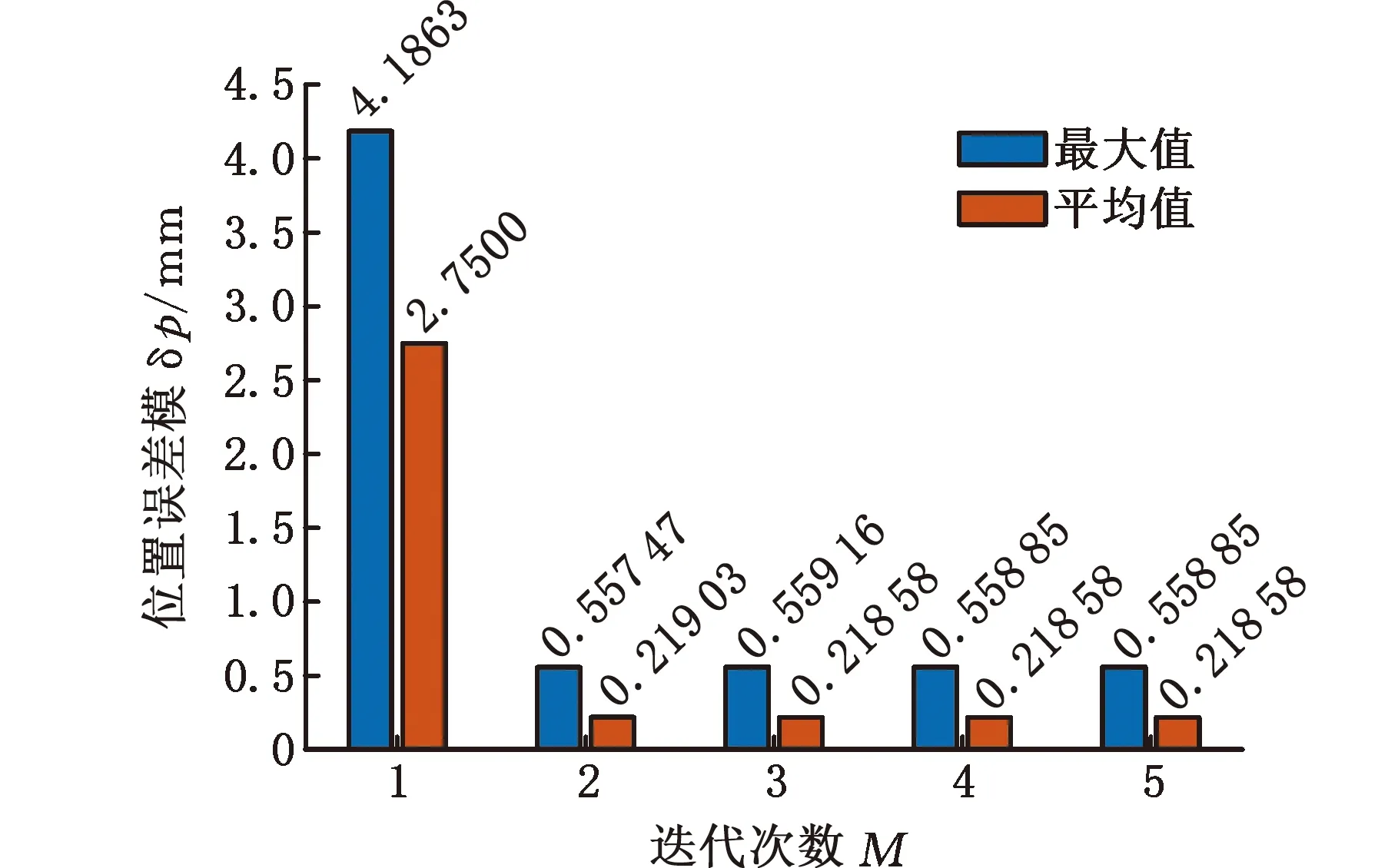
(a)迭代过程中位置误差模

(b)迭代过程中姿态误差模图7 迭代过程中位姿误差模Fig.7 Norms of pose errors in the iterative procedure

3.4 验证试验

在机器人的工作空间内随机生成20组关节变量，用来验证标定方法的正确性和有效性。通过激光跟踪仪测得末端执行器三个测量点的位置坐标值，如表2所示，并利用式(27)计算出末端执行器位姿的实际值。根据运动学参数的名义值计算出末端执行器位姿的理论值。根据运动学参数的标定识别结果计算出末端执行器位姿的标定补偿值。如图8所示，机器人位置误差模的最大值和平均值分别从4.4777 mm和3.1488 mm减小到0.6966 mm和0.2812 mm。姿态误差模的最大值和平均值分别从0.0183 rad和0.0166 rad减小到0.0031 rad和0.0018 rad。

表2 验证试验位置坐标Tab.2 The position coordinates for the verification test mm

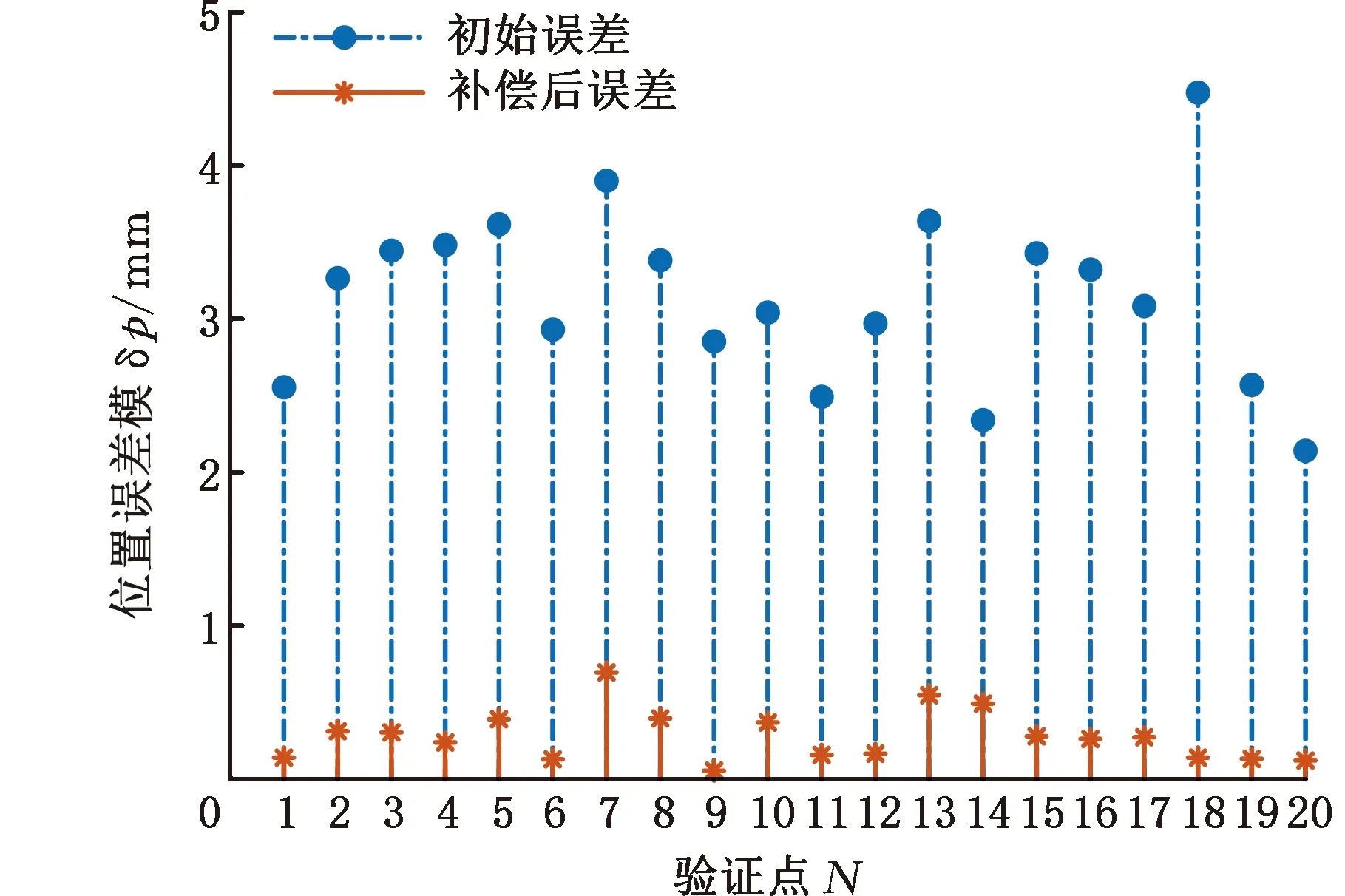
(a)验证点的位置误差模

4 结论

(1)基于指数积公式给出了一种以工具坐标系为参考系包含关节约束条件的位姿误差标定模型,避免了末端执行器位姿误差在基础坐标系表示时，误差模型中姿态误差与位置矢量的乘积项对参数识别精度的影响。

(2)以UR5机器人为标定对象，采用激光跟踪仪为测量设备，进行运动学参数标定试验。试验结果表明，经过参数标定，机器人位置误差模和姿态误差模的平均值分别降低了91.07%和89.16%，验证了该运动学参数标定模型的正确性和有效性。