海杂波条件异方差特性分析与波动信息提取

孙艳丽，姜星宇，刘宁波，陈 凯，王月香

（1.海军航空大学，山东烟台 264001；2. 91599部队，山东烟台 264000；3.鲁东大学，山东烟台 264025）

0 引言

海杂波是指海面对雷达发射电磁波的散射回波。一般来说，它通常被认为是1个干扰源，会影响有用信号的检测。由于海杂波具有随机性，通常被建模为1个随机过程。

根据场景的不同，使用的模型多为高斯分布、对数正态分布、韦布尔分布、K 分布、Pareto 分布、广义复合概率密度函数或球不变随机过程等，其中一些分布可能对实际海杂波分布有很好的拟合效果，但它们是时不变的，并且在很多情况下，雷达探测环境可能会突然发生变化，导致目标检测方法的性能在实际场景的应用中会有所下降。

实际上，海杂波可以被建模为1 个非平稳的自回归（AR）过程，以考虑时变，但现有的统计分布通常不适用于序列中出现冲激情况，也不适用于频繁出现海尖峰导致的重拖尾现象。

针对上述问题，本文采用广义自回归条件异方差（Generalized Auto Regressive Conditional Heteroskedasticity，GARCH）过程，将海杂波建模为1个具有波动聚集性的时间序列。模型利用过程历史特性来改进当前和预测未来的特性。GARCH模型常用于经济学中描述随时间变化的金融序列，以及用于声呐应用中的水下噪声建模，它的2 个主要特征是重拖尾概率密度函数和波动聚集性：重拖尾概率密度函数对于描述海杂波分布是有益的；波动聚集性则主要反映物理变化过程中大的变化往往紧随大的变化而来，小的变化往往紧随小的变化而来。本文基于雷达实测数据，给出雷达海杂波异方差特性建模的基本理论和过程，对海杂波特性进行深入分析并给出波动性提取结果，验证基于GARCH 模型的海杂波波动信息提取的可行性和有效性。本文所提出的特征提取方法可用于构造海杂波与目标差异特征空间，进而为基于波动信息的特征检测方法设计提供有效的特征支撑。

1 GARCH模型

GARCH 模型描述的是1 个序列的残差序列的方差随时间变化的情况，而这种方差随时间变化的特性即为异方差性。GARCH模型是在自回归条件异方差（Auto Regressive Conditional Heteroskedasticity，ARCH）模型基础上推广而来的。因此，本节首先简单介绍ARCH模型，在此基础上引出GARCH模型。

在实际雷达对海探测场景中，海杂波序列易出现长时相关性。对于具有长时相关性的残差序列ε而言，若仍使用ARCH 模型进行拟合，则会导致模型移动平均阶数过高，不仅参数估算比较困难，而且还大幅降低了ARCH( )模型的拟合精确度。针对这一问题，提出了GARCH 模型，简记为GARCH( ),，其表达式如下：

GARCH模型是在ARCH模型基础上增加了异方差函数h的阶自相关性，因而其对具有长时相关性的残差序列具有更佳的拟合效果。ARCH 模型实质上是GARCH 模型的1 个特例，ARCH()模型是=0时的GARCH(,)模型。

此外，通过消除GARCH 模型中的各项参数非负的约束的操作，Nelson 提出了1 种改进的GARCH 模型，即EGARCH模型；Engle等人提出了另一种改进的GARCH 模型，即GARCH-M 模型。由于序列的均值依赖于其波动特性，故称之为依均值GARCH 模型。无论是哪种改进模型，都是在原GARCH 模型基础上考虑了序列的长时相关性，以求真实地反映时间序列的实际情况。

本文重点关注低擦地角、高海况条件下海杂波时间序列的波动效应（局部序列的快速起伏特性），在处理海杂波序列前，应去除海杂波确定性趋势的影响，并将海杂波序列与式（1）和式（2）中表示残差序列的ε相对应，以便于采用GARCH模型描述，并提取序列的波动趋势。

2 序列异方差性检验

采用ARCH 或GARCH 模型描述时间序列，首先需要对时间序列进行异方差性检验，只有在具有这一效应的前提下才可建模。常用的异方差性统计检验方法是PQ检验法。

3 雷达实测数据验证与分析

本文所采用的回波数据来源于加拿大IPIX 雷达（X 波段全相参雷达），经过1993—1998 年间的改造，其得到的高分辨率雷达数据已经成为测试雷达信号处理算法的重要数据。1998 年的IPIX 雷达数据是在加拿大格里姆斯比镇安大略湖岸边采集得到的，222个数据集包含了不同海况和气象等条件下的实测数据。IPIX雷达参数，如表1所示。

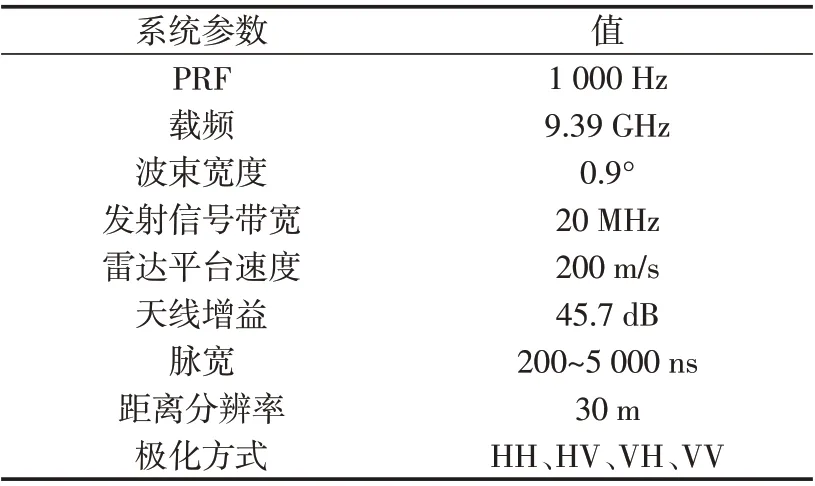
表1 IPIX雷达参数Tab.1 Radar parameters

低海况和高海况2种条件下的实测海杂波时间幅度图，如图1所示。

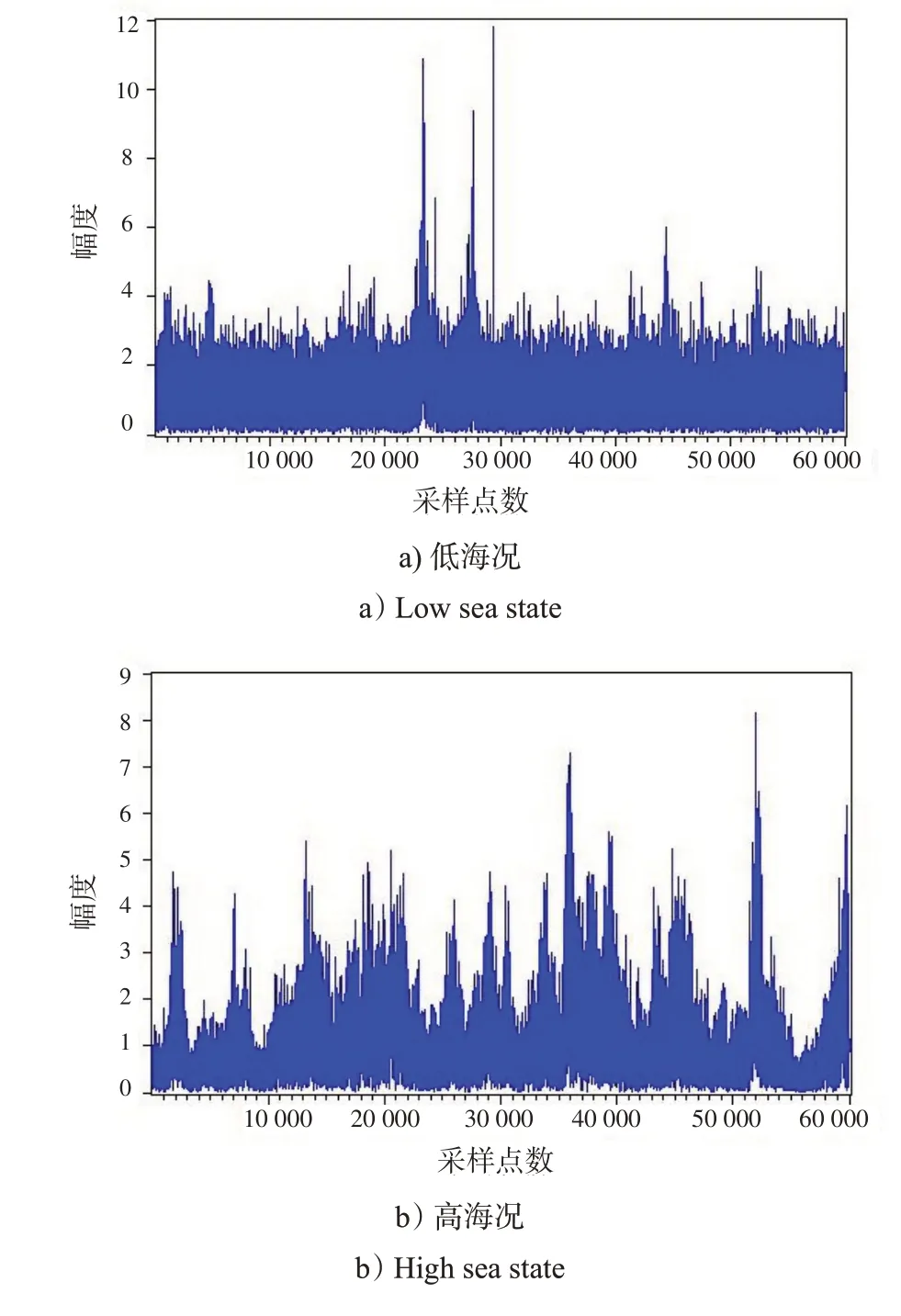
图1 海杂波实测数据Fig.1 Sea clutter measurement data

通过图1的对比可以发现，在不同海况条件下，海杂波呈现明显的波动起伏差异性。低海况数据对应的海况等级约为1～2 级，有效波高范围为0.1～0.5 m；高海况数据对应的海况等级约为4 级，有效波高范围为1.25～2.5 m。

雷达海杂波非平稳特性通常根据分段海杂波序列的均值和方差进行判断。这里采用HH极化条件下19980304_152453_ANTSTEP 数据为例进行说明。取第1距离单元中具有60 000个采样点的海杂波序列作为分析对象，将序列划分成若干个长度为2 000 采样点的海杂波序列段，相邻近数据段的重叠率为50%，绘制该距离单元中所有海杂波序列段的均值和方差变化情况，如图2所示。

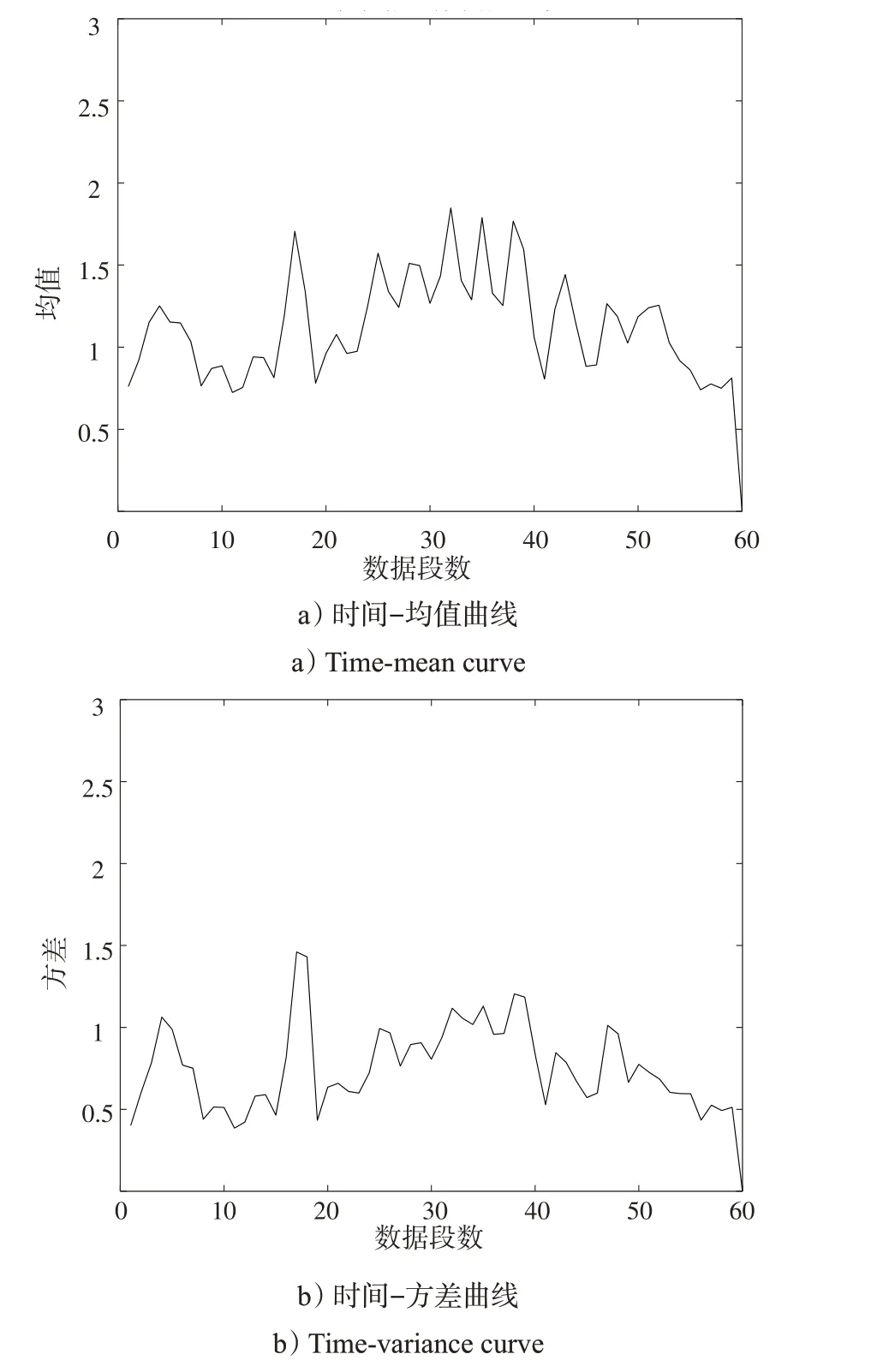
图2 海杂波非平稳性Fig.2 Sea clutter nonstationarity

由图2 可知，海杂波序列的均值和方差随着时间起伏，即具有时变性，因而海杂波序列是非平稳序列。

由第1、2 节可知，海杂波序列是否可用GARCH模型建模需进行检验，而检验方法实质上就是判断海杂波序列是否具有相关性，以及呈现的是长时相关性还是短时相关性。海杂波的时间相关性是指相同距离单元在不同采样时刻之间的相关性。这里使用自相关系数和偏自相关系数来定量描述海杂波的时间相关特性，并以1/e作为门限，判断强弱相关性是否存在，且认为在小于相关时间的尺度（延迟阶数）内海杂波序列存在强时间相关性。

图3和图4给出了HH、VV、HV和VH 4种极化方式下实测海杂波序列的自相关系数和偏自相关系数。不同组的海杂波数据具有相似的结果，这里仅展示了其中1组数据多个海杂波单元的相关系数平均后的结果。

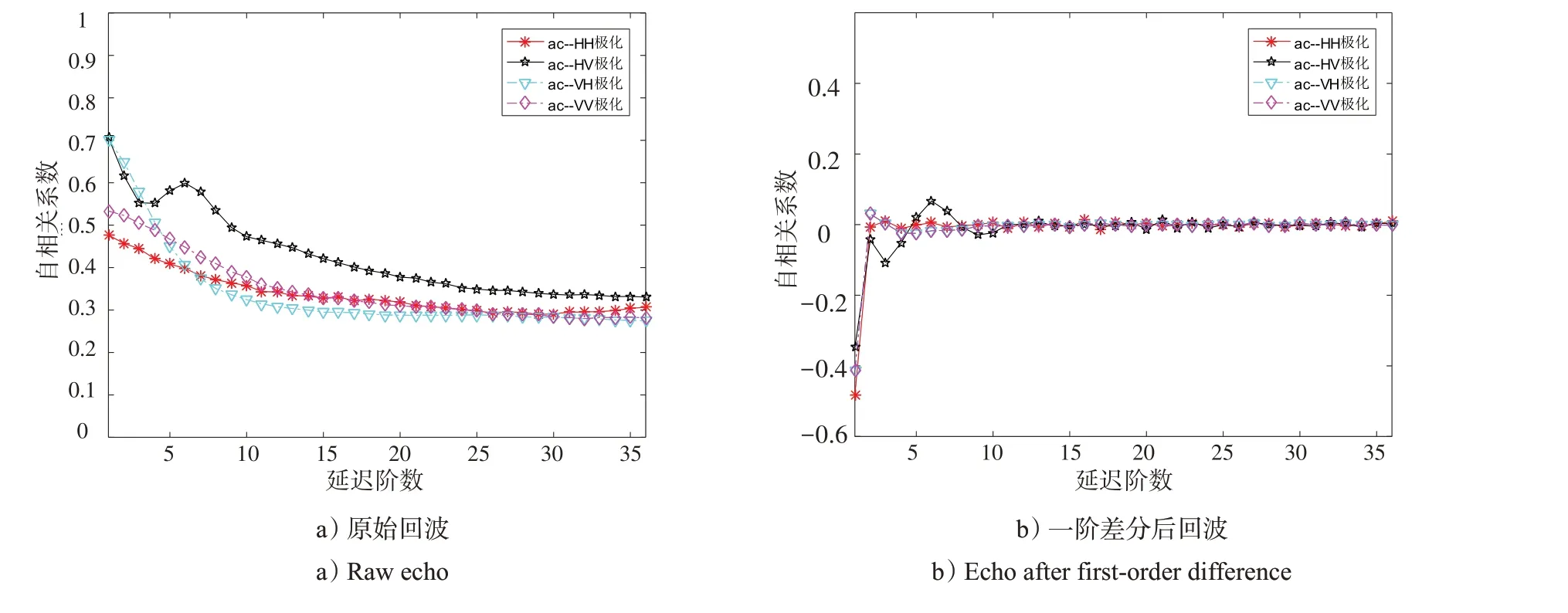
图3 不同极化方式下平均自相关系数曲线Fig.3 Mean autocorrelation coefficient curves under different polarization modes

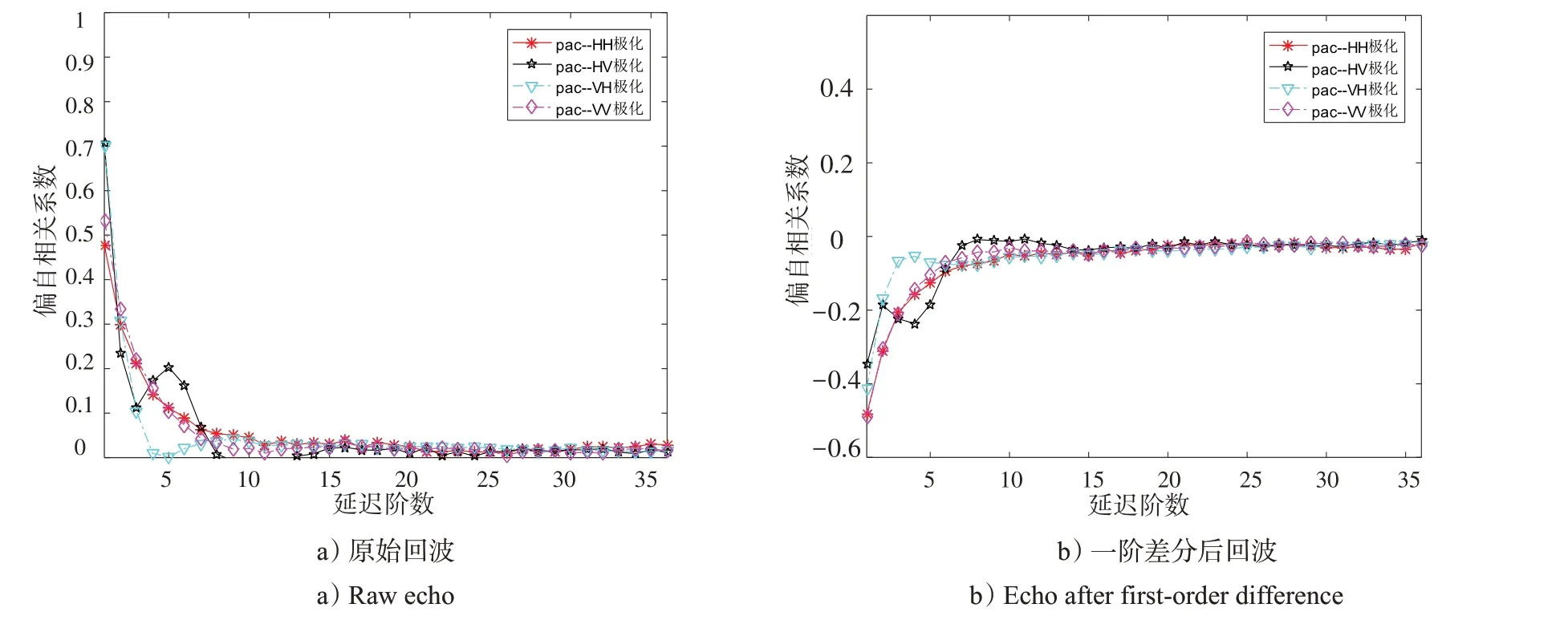
图4 不同极化方式下平均偏自相关系数曲线Fig.4 Mean partial autocorrelation coefficient curves under different polarization modes

由图3和图4可知，海杂波相关系数曲线在经历1个短时间的快速下降后会有1个较长时间的缓慢衰减过程，这说明海杂波序列具有短时强相关性和长时弱相关性。结合海杂波产生的物理机制可知：海杂波散斑分量易呈现强相关性，但相关时间持续比较短，在几毫秒至几十毫秒量级；海杂波纹理分量则具有较长的相关时间，相关性相对较弱，但持续时间较长，一般在几秒以上。不同极化方式下，通过海杂波的相关性对比可知，在短时间间隔内交叉极化（HV、VH）方式下的强相关性强于同极化（HH、VV）方式，而在一阶差分条件下，海杂波时间相关性变得很弱，可以近似认为不相关。无论是强相关还是弱相关，总体来看，海杂波时间序列都呈现长时相关性。根据前文给出的前提条件和异方差性判断方法，可以得知海杂波序列需采用GARCH模型进行建模分析并提取其波动信息。

在上述分析基础上，可采用GARCH 模型进行实测数据拟合，提取其波动（快速起伏）信息。由于实测数据具有随机性，因而在采用GARCH 模型对不同的数据进行拟合时，阶数和往往也随数据发生变化，因而，这里需要针对每组数据进行多次重复运算。具体建模过程为：采用某种阶数和组合下的GARCH(,)模型拟合实测数据，并将实测数据幅值与模型计算结果相减，得到残差序列，然后对残差序列进行异方差性检验，若残差序列仍具有相关性，则步进提高阶数和的值，形成新的GARCH(,)模型，再次计算得到残差序列，直至残差序列为白噪声时（通过PQ 检验接收假设），停止运算，表明当前序列的所有波动信息完全被提取。图5 给出了数据19980304_152453_ANTSTEP 的波动信息提取结果。这里须说明的是，对其他组海杂波数据进行波动性提取，可以得到类似的结果，经多组数据处理结果统计发现，阶数和取值在1～4 范围内即可对波动性信息进行很好的提取，限于篇幅，这里只给出1组数据的波动性信息提取结果。

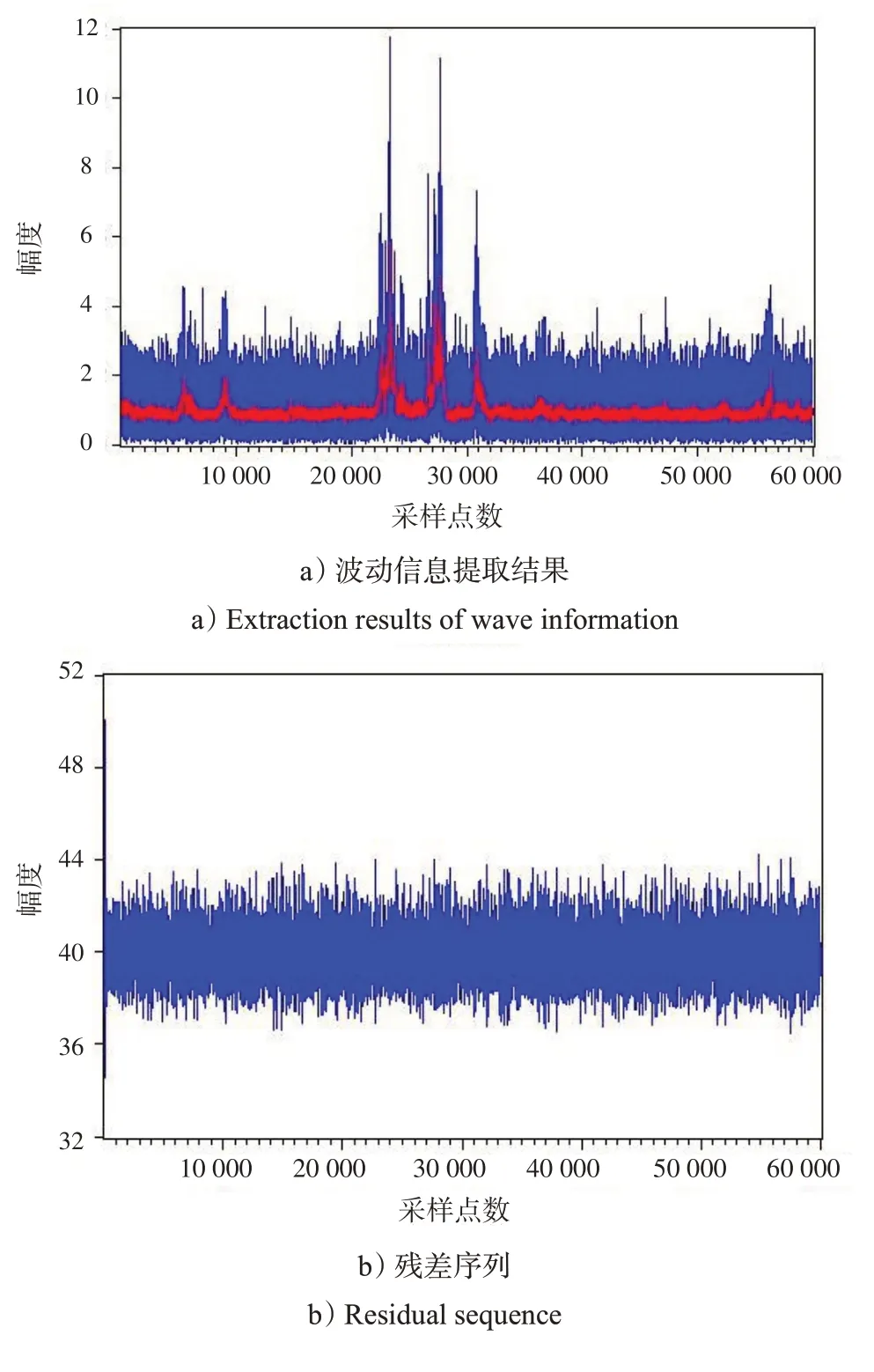
图5 实测数据处理结果Fig.5 Processing results of measured data

通过图5 可以发现，海杂波序列的波动信息得到了很好的提取，如图5a）中红色曲线（在灰度显示模式下对应浅灰色曲线）所示。同时，图5b）所示的残差序列也通过了异方差性检验，呈现白噪声特性。

4 结论

本文将GARCH模型引入雷达实测海杂波数据建模中，在判定海杂波序列的非平稳性和长时相关性基础上，通过GARCH 模型阶数步进搜索结合残差序列方差齐性检验，实现海杂波数据的波动信息提取。经实测数据验证，本文提出的波动信息提取方法，可以很好地提取实测海杂波数据在局部区域或时间段内的波动信息，可以为海尖峰抑制和高海况下目标检测性能的提升提供支持。