基于改进萤火虫算法的水库多目标调度决策研究

兰 回 归，李 英 海，2，李 清 清，孟 虹 池，杨 苑

(1.三峡大学 水利与环境学院，湖北 宜昌 443002； 2.三峡大学 三峡库区生态环境教育部工程研究中心，湖北 宜昌 443002； 3.长江科学院 水资源综合利用研究所，湖北 武汉 430010)

0 引 言

流域控制性水库调节能力强、电站装机容量巨大，在防洪减灾、发电、水量调度以及缓解局部地区生态环境退化中发挥了关键作用，进行水库多目标调度意义重大[1]。水库多目标调度具有非线性、高维度、多约束、目标间存在协调与对立冲突等特性，其优化难度一般优化方法难以应付，对于优化求解产生的Pareto方案集如何进行科学决策同样是水库多目标调度研究的重要组成部分[2]。

很多学者对水库多目标调度以及调度方案集决策相关问题进行了研究。针对水库多目标调度问题，可以通过约束法、权重法将多目标问题转化为单目标问题进行求解，但是这种方法求解过程繁琐且带有主观性[3]。基于Pareto理论的多目标进化算法凭借其高效的求解效率以及简单的算法原理成为求解水库多目标调度的研究热点，目前研究者们多采用遗传算法(Non dominated Sorting Genetic Algorithm-Ⅱ，NSGA-Ⅱ)、差分进化算法(Multi-objective Differential Evolution algorithm，MODE)、粒子群算法(Particle Swarm Optimization，PSO)等进行水库多目标调度求解。方国华等[4]构建水库生态调度模型，以生态保护程度和发电量最大为目标，采用NSGA-Ⅱ算法进行求解，得到了兼顾生态和发电效益的调度方式。陈学义等[5]采用改进的PSO算法进行水库多目标调度，结果表明改进后算法具有更好的收敛性。王学敏等[6]构建三峡水库生态调度模型并采用MODE算法进行求解获得多个符合生态效益评价标准、分布均匀、收敛性较好的非劣调度方案。多目标萤火虫算法(Multi-objective Firefly Algorithm，MOFA)作为一种新颖、高效的进化算法，具备结构简单、参数少以及优化能力强等特点，但在水库多目标调度领域鲜有运用。

目前进行水库多目标调度方案决策的方法较多，层次分析法基于专家主观意愿进行决策，是方案决策的经典方法，但是没有考虑客观因素影响。模糊集理论[7]、TOPSIS法等通过对方案集数据进行分析得出客观的决策方案[8]。理想均变率法[9]、理想点法[10]等通过对调度目标进行定性定量分析，优选出综合效益最优的方法。如何充分考虑决策方案在方案集中的综合效益以及选择该方案后的遗憾程度，同时考虑决策者主观意愿以及决策指标的客观特征是目前亟待解决的问题。多准则妥协解排序法(VlseKriterijumska Optimizacija I Kompromisno Resenje，VIKOR)作为一种综合评价方法可以同时考虑评价对象群体效用值以及个体遗憾值，得出距离理想解最近的折中解，被广泛运用于多属性决策领域[11]。

基于上述问题，本文以水库发电量效益以及生态效益为目标，构建多目标调度模型，对经典MOFA算法收敛性不好、易早熟收敛的不足进行改进，提出变异精英多目标萤火虫算法(Mutant Levy Random Elite Multi-objective Firefly Algorithm，MLRE-MOFA)，进而采用VIKOR方法进行方案集决策，并采用组合权重系数进行指标赋权，考虑主客观因素的影响，同时在折中最大化群体效益和最小化个体遗憾的基础上寻求最优解，最终将其应用于三峡水库多目标联合调度实例中验证该方法的有效性。

1 水库发电-生态多目标调度模型

在水库多目标调度模型中，以发电量最大作为发电效益目标，以修正全年流量偏差函数(Amended Annual Proportional Flow Deviation，AAPFD)作为生态效益目标的度量，该指标值越小表示水库调度后流量变化对河流生态系统的影响越小，河流生态环境越好[12]。

(1) 年发电量最大目标。

(1)

式中：F1为总的发电量；Δt为第t时段长；T为时段数；k为水库出力系数；qt为水库第t时段发电流量；Ht为水库第t时段发电水头。

(2) 生态AAPFD值最小。

(2)

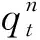
约束条件主要包括：

(1) 水量平衡约束。

Vt+1=Vt+(It-qt)Δt

(3)

式中：Vt和Vt+1分别为t时段初末库容；It，qt分别为t时段水库的入库流量和出库流量。

(2) 水库水位约束。

Zmin，t≤Zt≤Zmax，t

(4)

式中：Zmin，t和Zmax，t分别为水库t时段的最小水位和最大水位。

(3) 下泄流量约束。

qmin，t≤qt≤qmax，t

(5)

式中：qmin，t和qmax，t分别为第t时段最小、最大下泄流量。

(4) 电站出力约束。

Nmin，t≤Nt≤Nmax，t

(6)

式中：Nmin，t和Nmax，t分别为时段最小、最大出力。

2 模型求解方法

2.1 改进多目标萤火虫算法

2009年英国学者Yang提出萤火虫算法(Firefly Algorithm，FA)，该算法源于模拟自然界萤火虫在夜晚群聚活动的自然习性而产生，主要用于单目标优化[13]。为解决多目标问题，Yang等又提出了多目标萤火虫算法(MOFA)，其核心思想是：亮度低的萤火虫被亮度高的萤火虫吸引，向亮度高的萤火虫移动，根据位置更新公式更新原来的位置，移动距离大小根据吸引度决定，吸引度大小与相对亮度成正比，根据各个目标之间的支配关系，得到非支配解，将其放入Pareto前沿，通过多次迭代，一般可以得到近似帕累托前沿的n个非支配解集，从而实现寻优[14]。

萤火虫个体i与j的相对亮度为

Iij=I0e-γrij

(7)

式中：I0为萤火虫本身位置的亮度；γ为吸光度系数；rij为萤火虫之间的距离。

萤火虫个体i与j之间的吸引度为

βij=β0e-γrij

(8)

式中：β0为萤火虫最大荧光亮度处的吸引度。

萤火虫i的位置更新公式为

xi=xi+βij(xj-xi)+αεi

(9)

式中：α为步长因子，εi为均匀分布的随机值。

为进一步增强算法的解空间搜索能力，加快算法的收敛速度，本文引入莱维飞行以及随机游走扰动项对算法的随机值εi进行改进，建立精英档案引导机制，使萤火虫个体迅速向Pareto前沿靠拢，并增加个体变异机制以增强算法跨越局部最优解的能力。改进的多目标萤火虫算法(MLRE-MOFA)流程如图1所示。

(1) 莱维飞行与随机游走扰动项。莱维飞行是一类非高斯随机过程，包含短步长近距离搜索与大步长远距离搜索[15]。前期将莱维飞行作为算法的随机扰动项可以利用其大步长远距离搜索的特性，进行全局搜索。

随机游走其概念接近几何布朗运动，表现为一种连续随机涨落过程[16]，后期将随机游走作为算法的随机扰动项可以加强萤火虫个体的局部探索能力，提高算法跨越局部最优值的性能。

(2) 档案精英解引导萤火虫移动。经典MOFA算法中，被支配萤火虫个体向支配个体之间移动依赖于两个体之间的相对亮度与吸引度，没有充分利用档案精英解来指引萤火虫个体的移动，在此基础上将档案精英解引入萤火虫个体的位置更新过程，使被支配萤火虫个体向支配萤火虫移动的同时不断靠近档案精英解，加速算法的收敛。改进后萤火虫个体位置更新公式为

(10)

式中：xg*(t)为随机取出的档案精英解；s为考虑莱维飞行和随机游走的随机扰动项。

(3) 个体变异。为了进一步增强算法的性能，加快算法的求解效率，使其跳出局部最优解从而达到全局最优解，在萤火虫个体移动的过程中增加变异机制，以增强算法搜索性能。萤火虫个体i移动过程中产生一个随机数r∈[0，1]，若r的值小于变异概率pm，则个体i发生变异，个体i变异通过公式(11)和(12)实现。

xi=xi+ψ(Ub-Lb)

(11)

(12)

式中：Ub为约束上限；Lb为约束下限；μi∈[0，1]为随机数；η为常系数，本文η=20。

2.2 算法验证

为了验证MLRE-MOFA算法的有效性，选用测试函数进行算法验证。测试函数选用国际上具有代表性的多目标测试集ZDT系列的ZDT1、ZDT2、ZDT3函数对本文算法的收敛性指标ω和多样性指标Δ进行测试[17]，并同NSGA-Ⅱ、MOFA算法进行比较。ZDT1为连续凸函数，ZDT2为连续凹函数，ZDT3为非连续函数，各个测试函数决策变量数为30，目标函数个数为2。

各测试算法设置种群规模为30，迭代次数250次，γ=1，α=1，β0=1，MLRE-MOFA算法的变异概率pm=0.05。各个算法独立运行20次，取指标ω与Δ的均值与方差，结果如表1所列。其中NSGA-Ⅱ的结果数据引自文献[17]。

由表1可知，MLRE-MOFA算法的收敛性指标ω以及多样性指标Δ的均值均小于其他算法，表明改进算法收敛性以及解集的多样性优于其他算法，经过对经典MOFA算法的改进有效改善了算法早熟收敛和易陷入局部最优解的缺陷。同时改进算法ω、Δ的方差近似为0，表明了MLRE-MOFA算法稳定性强。

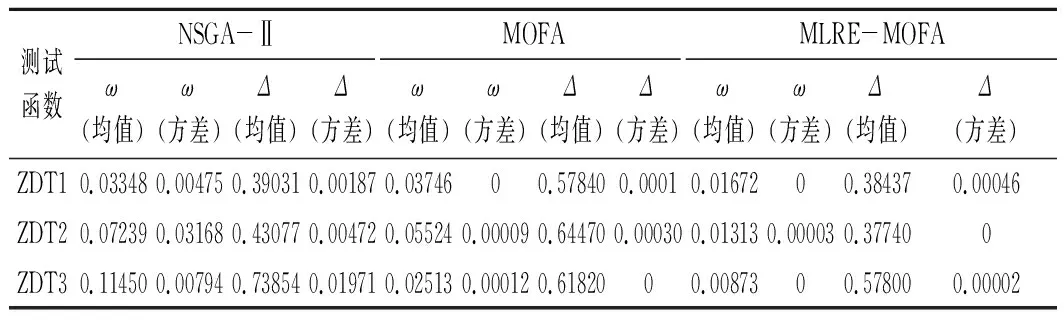
表1 算法测试结果Tab.1 Three algorithms′ test results

2.3 改进VIKOR决策方法

VIKOR决策方法是针对备选方案存在多个性能评价指标且多个指标间可能存在冲突性的多方案多指标综合优选排序方法，采用该方法进行决策能综合考虑决策方案的群体效益以及选择该方案的遗憾程度[18]。采用VOKIR方法得到各个评价指标的权重对于方案优选的合理性至关重要，为了克服单一赋权法的缺陷，将主观权重与客观权重进行组合优化，进行决策时既考虑决策者的主观偏好以及决策指标客观信息，又能够反映决策方案的群体效益以及选择该方案时的遗憾程度。

采用VIKOR算法进行方案决策的主要步骤如下：① 构造初始决策矩阵，并对其标准化；② 确定正负理想方案；③ 组合权重计算。

主观权重通过专家经验确定，客观权重通过变异系数法进行赋权，通过指标变异程度大小来对指标赋予不同权重。第j个评价指标变异系数计算步骤如下：

(1) 第j个评价指标的变异系数计算。

(13)

(2) 第j个评价指标客观权重计算。

(14)

(3) 组合权重计算。

(15)

式中：lj为主观权重。

(4) 计算群体效益值Si、个别遗憾值Ri以及利益比率值Qi。

(16)

(17)

(18)

(5) 方案排序。根据求解的Si，Ri，Qi的值对各个评价对象排序，其值越小，则对应评价对象越好。若求解的结果满足如下条件，可以单独根据Qi的值进行排序：①Q1-Q2≥1/(m-1)，其中Q1表示最优方案的综合取值，Q2表示次优方案的综合取值，1/(m-1)为可接受门槛值，m为待评价方案个数。② 最优方案Q1的Si值或者Ri值优于次优方案Q2。

若上述条件不能同时满足，则得到妥协解：若不满足条件①，则Q1，Q2，…，QN为备选妥协解，由QN-Q1<1/(m-1)得到N的值；若不满足条件②则Q1，Q2均为妥协解。

3 实例计算

三峡水利枢纽具有巨大的防洪、发电、航运等综合效益，其水库蓄水与电站发电必然改变下游河流的自然特性，对流域生态环境造成多方面的影响[19]。本文采用MLRE-MOFA算法以及组合权重改进的VIKOR决策方法，开展三峡水库发电-生态多目标调度决策研究。数据选取三峡水库1950～2020年实测入库流量数据对其进行水文频率分析，选取50%的流量作为典型平水年，进行分析计算。

3.1 多目标调度优化求解

本文采用50%频率年来水过程作为典型平水年，以月为计算时段进行多目标优化调度计算。三峡水库下游河道生态流量数据采用逐月频率法，计算出基于统计规律的生态流量，进而结合长江下游四大家鱼以及中华鲟的适宜繁殖流量，取各月流量上下限均值作为综合生态流量指标，对于有鱼类繁殖的月份，采用鱼类繁殖流量的上下限均值作为当月的综合生态流量指标[20]。三峡水库下游生态流量过程如表2所列。

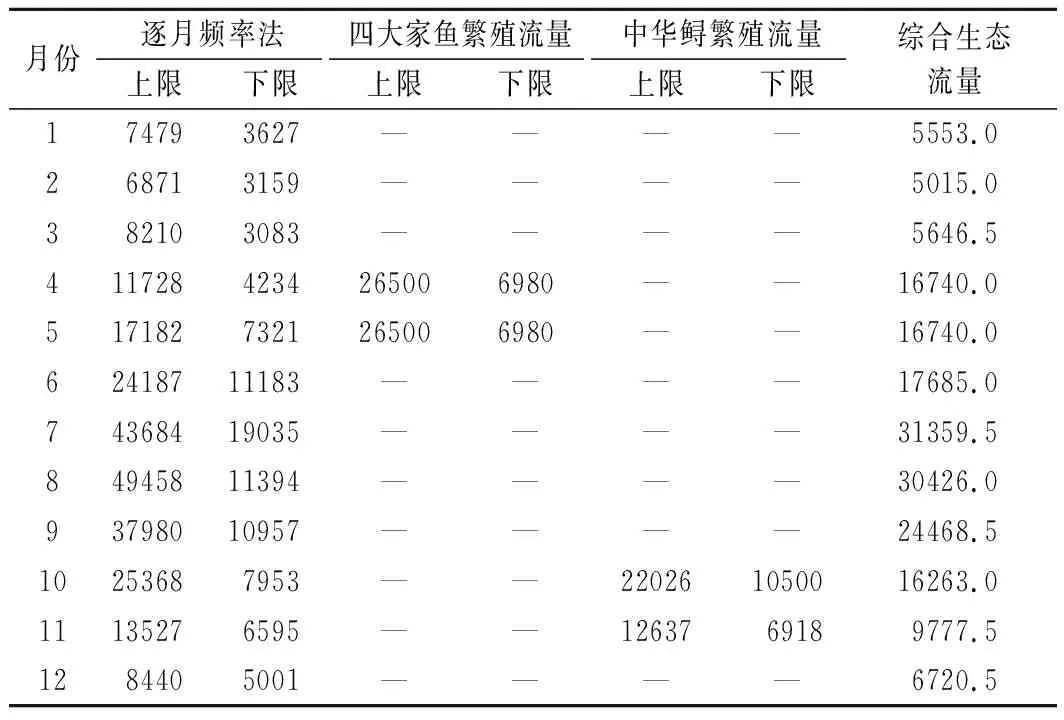
表2 三峡水库下游生态流量过程Tab.2 Ecological flow process in the lower reaches of the Three Gorges Reservoir m3/s

按照三峡水库调度规程，三峡水库正常蓄水位175.00 m，防洪限制水位145.00 m，枯期消落水位155.00 m。保证出力499.6万kW，装机容量2 250万kW。1～5月水库水位考虑多方需求条件下可逐步消落，4月末水库水位不低于枯期消落水位，5月25日不高于155.00 m。汛期水库按照防洪限制水位145.00 m控制运行，6月10日消落到汛限水位。水库开始兴利蓄水时间不早于9月10日，一般情况下9月底控制水位162.00 m，10月底可蓄至175.00 m。

8月份除实施防洪和应急调度外，水库日均出库流量尽量不小于18 000 m3/s。9月份水库来水大于10 000 m3/s时，按不小于10 000 m3/s下泄，来水流量在8 000～10 000 m3/s之间时，按来水流量下泄，来水小于8 000 m3/s，适当补水至8 000 m3/s。10月蓄水期间，水库下泄流量按不小于8 000 m3/s控制。蓄满年份，水库1～2月下泄流量按不小于6 000 m3/s控制。

在采用MLRE-MOFA算法进行求解时，以三峡水库时段库水位作为萤火虫个体决策变量进行编码，每个萤火虫个体代表一种水位调度过程，每个萤火虫个体有12个编码值。萤火虫移动过程中，萤火虫各个时段编码值严格在三峡水位约束范围内变动，超出边界值则取边界值，采用调度目标值作为萤火虫个体的亮度，当算法计算过程中出现出力以及发电流量不满足时段约束时，对调度目标值进行惩罚以减小萤火虫亮度，确保生成的非劣解的合理性。参考算法验证时算法参数设置经验以及动态规划(DP)计算得出的理论Pareto前沿，经过反复计算测试，确定MLRE-MOFA算法参数设置如下：种群规模16，迭代次数1 000次，γ=1，α=1，β0=1，pm=0.05，调度方案集结果如图2所示。由图2可知：三峡水库发电量从905亿kW·h增加到930亿kW·h，生态AAPFD值由0.68增加至0.86。发电效益与生态效益反比关系明显，可见为了保证水库下游河道的生态效益，水库的发电量受到了影响。

将MLRE-MOFA算法求解的结果与MOFA算法以及动态规划求解的Pareto前沿进行对比(见图2)。图2的调度结果表明：在各算法参数设置相同时，MLRE-MOFA算法得到的Pareto前沿更加接近DP求解得到的Pareto前沿，表明MLRE-MOFA算法收敛性更优，且前沿均匀分布在整个解空间，较未改进时算法性能提升明显。

将经典MOFA算法以及改进后MLRE-MOFA算法独立运行20次，计算调度方案集的收敛性指标ω和多样性指标Δ，结果如表3所列。

表3的计算结果显示，经过对MOFA算法改进，MLRE-MOFA算法的调度方案集的收敛性和分布性均得到提升，且算法的稳定性较好。

表3 实例计算算法测试结果Tab.3 Algorithm test by example calculation

3.2 方案优选结果分析

进一步的，采用组合权重改进的VIKOR方法进行方案优选。其中主观权重由专家凭经验确定，客观权重采用调度目标变异系数确定，按式(15)计算指标综合权重，根据评价指标的综合权重，当决策者基于不同偏好进行主观赋权时得到的综合权重结果如表4所列，方案决策结果如表5所列。

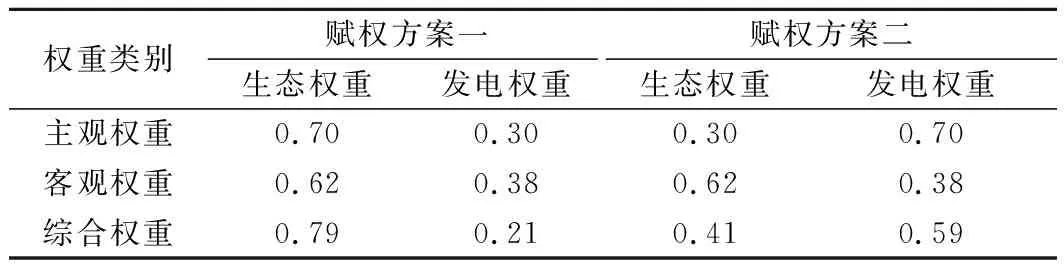
表4 综合权重计算结果Tab.4 Comprehensive weight results

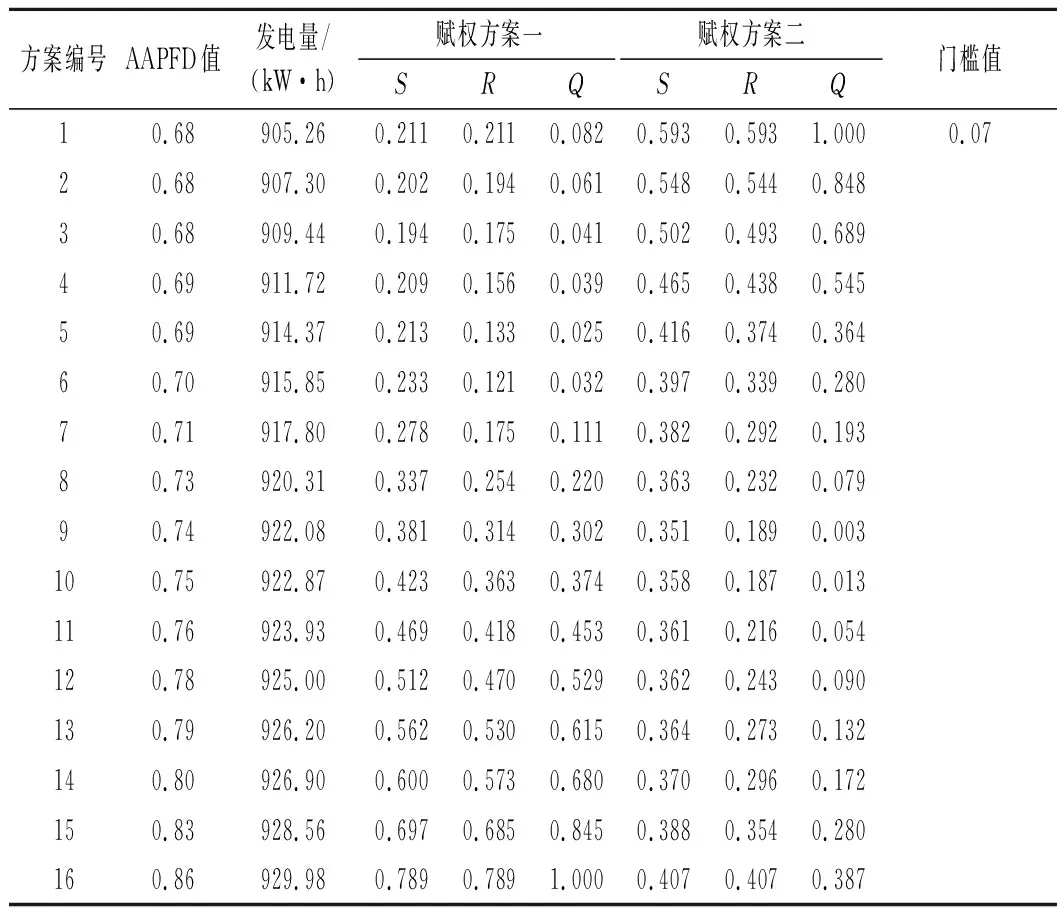
表5 方案决策结果Tab.5 Scheme optimization results

当决策者偏向于生态效益目标时，采用赋权方案一的赋权方法。从表3的计算结果可以得出，方案5的Q值最小，综合效益最优，方案6的Q值略大于方案5，为次优方案。方案5与方案6的Q值差为0.007，未超过门槛值0.07，不满足上述VIKOR决策条件(1)，因此得到妥协备选方案为方案1～7。根据VIKOR方法决策特点，认为当决策者偏向于生态效益时，方案1～7同为综合效益最优且个体遗憾最小的方案，方案7的发电量在4个方案中最大，因此选择方案7为最优调度方案。当决策者偏向于发电效益，同理可以得出此时最优调度方案为方案11。采用不同决策意愿进行调度得到的最优调度方案结果如图3～5所示。

通过图3～5的调度过程可以看出，不同调度方案调度过程均满足三峡水电站调度约束条件要求。从图3水位过程可以得出，当决策者期望获得更多发电效益时，决策者更加倾向于保持较高水位运行，图4的结果显示在消落期和蓄水期，采用方案11的出力比方案7大，表明当决策者倾向于发电效益时，在消落期和蓄水期会尽可能提高出力。图5展示了不同调度方案各个月份的出库流量大小，方案11的出库流量在消落期以及蓄水期来水较多的月份相对方案7大，表明当决策者期望获得更多发电效益时，在水库消落期以及蓄水期会下泄更大的流量。表6的调度结果可以得出方案7的年发电量较方案11少，但是方案7的生态效益优于方案11。上述分析结果验证了本文所提的优选方法的有效性。

表6 方案7，11的调度结果Tab.6 Scheduling results of scheme 7，11

4 结 论

针对水库多目标调度决策问题，本文提出了MLRE-MOFA算法以及组合权重改进的VIKOR决策方法进行方案优选，并通过三峡水库调度实例分析进行验证。结果表明：将莱维飞行、随机游走随机值以及变异机制引入多目标萤火虫算法可以平衡算法全局搜索以及局部搜索能力，避免算法陷入早熟和局部最优的缺点。精英解引导萤火虫个体移动可以提高算法向Pareto前沿收敛的速度，提升算法求解的效率。将MLRE-MOFA算法和改进VIKOR决策方法组合，能够在优化求解水库调度的同时，从Pareto最优方案集中优选出群体效益最优且个体遗憾最小的调度方案。

随着水库功能不断完善以及流域发展的需求，如何考虑不同调度目标之间的博弈过程进行水库多目标调度，还有待开展进一步研究。