高压水射流清障施工盾构掘进面稳定性研究

吴 志 强，李 瑞 红，陈 城，李 忠 艳

(1.南通职业大学 建筑工程学院，江苏 南通 226007； 2.苏州大学 轨道交通学院，江苏 苏州 215000)

0 引 言

当前中国地铁建设方兴未艾，伴随着地铁线路的增多，新建隧道遇到既有障碍物的情况会越来越普遍，传统的清障方法成本高、工期长且对周边环境影响大[1-3]。针对上述问题，国内外学者通过对盾构机刀盘进行改进，使盾构直接切削钢筋混凝土桩技术得到了迅速发展。北京交通大学袁大军团队[4-5]通过实际工程验证了盾构直接切桩的可行性。但直接切削钢筋混凝土时，钢筋多被拉断，很难被直接切断，故钢筋极易缠绕在刀盘上，极大地影响了切割效率，严重时还会造成卡机现象，对工程施工带来了困难和安全隐患。因此，有效切断钢筋，避免钢筋过长缠绕在刀盘上对实际施工意义重大。

基于此，本文介绍一种新型切割技术——水刀切割工法，即高压水射流切割技术，目前该技术的研究工作尚处于起步阶段。Hood[6]在刀具上安装了水射流装置，通过切割岩石试验发现，经水射流切割之后，刀具再切割时刀头的受力得到了明显的改善。Kotwica[7]在机械刀具上安装水射流辅助装置进行破岩试验，发现水射流可以减少30%以上的截齿边缘磨损量。Ozcelik等[8]研究发现水压、转速等因素对破岩效率影响较大。Ciccu等[9]在圆盘破岩试验中使用了水射流技术，表明在有水射流参与的工况下沟槽材料的去除率得到了极大的提升。Li等[10]通过水射流数值模型发现高压水射流对岩石的应力传播速度极快。卢义玉等[11]进行了水射流切割岩石试验，发现水射流切割过的岩石强度下降较大。陈跃强[12]将水磨料和截齿结合起来，通过试验证明其有利于提高破岩效率。庄欠伟等[13]通过磨料水射流切割钢筋混凝土试验发现磨料水射流联合盾构刀具能有效解决钢筋缠绕问题。

综上所述，国内外学者对水刀切割工法的研究主要集中在能否切割以及如何提高切割效率等方面，而对于在水刀切割工法下掘进面稳定性问题尚未看到相关文献报道。由于水刀切割是非接触方式，故在清障的过程中无法在掌子面上施加支护压力，由于没有支护压力，更容易出现掘进面失稳，因此亟需研究高压水射流清障施工条件下盾构掘进面的稳定性。

基于此，本文以目前工程中越来越多遇到的钢筋混凝土桩为研究背景，在考虑桩-土相互作用的基础上，提出水刀切割下掘进面支护力计算模型和超前加固长度计算公式。然后结合数值软件，在合理选取模型参数的基础上，验证了理论计算模型的合理性，并在其基础上，研究了土体内摩擦角、埋深比以及加固长度等参数对支护力的影响规律，研究结果可为后续工程的设计和施工提供理论基础。

1 水刀切割工法

水刀切割工法，即高压水射流切割技术，通过超高压喷射出的水流混合磨料来切割障碍物，相较于传统的盾构切割，其不会产生较大的热效应，且对环境无污染。

目前水刀切割技术在中国隧道建设领域还处于探索阶段，尚未有切割障碍物工程的运用。而日本在实际工程中运用水刀对障碍物进行了破除并取得了良好的工程效益。他们主要是将水刀切割系统安装在盾构刀盘上(即DO-Jet工法)，在掘进过程中遇到障碍物时会先喷射出超高压水流对障碍物进行切割，从而实现盾构刀盘对障碍物的快速切削破除[14]，具体装置见图1。

图2和图3展示了这种施工工法中核心的两个系统，分别为“地基改良系统”和“切割/清除系统”。

2 三维理论模型的建立

2.1 基本假定

本节首先构建盾构掘进面的三维理论模型(见图4)，采用极限平衡法对掘进面的稳定性进行理论推导，求得支护压力解析解。为便于计算，本文基于以下假定：

(1) 将滑动体上方土体和结构的荷载简化为均布荷载σs；

(2) 假定滑动体沿与水平面呈一定角度的斜截面滑动(即沿直线滑动)；

(3) 由于加固体的黏聚力、内摩擦角等参数明显大于原状土，根据已有关于内摩擦角与滑动角关系的研究，滑动角可近似为θ=45°+φ/2，故假设θ2>θ1。

2.2 理论推导

为便于受力分析，先绘制出掘进面平面受力模型，如图5所示。掘进面发生失稳时，滑动体的高度和宽度即为隧道的高度D和宽度B，长度假定为L，方向沿着隧道掘进方向，滑动角根据土体性质的不同分为θ1和θ2。以整体滑动体作为受力分析对象，所受到的作用力主要包括以下几部分：未加固区和加固区土体的自重应力G1和G2，掘进面的支护力S，上覆土层施加在滑动体上的竖向力σs，滑动体所受到的侧向摩擦力Ts1和Ts2，斜面摩擦力T1和T2，斜面正应力N1和N2。

考虑到滑动体分为加固区和未加固区，故对其进行分区域求解。

(1) 未加固区域。对于未加固区域的极限支护压力的求解，主要采用水平条分法，如图6所示，具体的推导求解过程可以参考文献[15]。

极限支护压力S1：

(1)

(2) 加固区域(见图7)。未切割时，加固区处于极限平衡状态时，受到的作用力有：掘进面推力S2，未加固区域的推力S1，滑动体外部桩的作用力P1和P2(水平向右)，滑动体内部桩的摩擦阻力Fs(竖直向上)，加固体的重力G2，侧摩阻力Ts2。根据水平力平衡条件可得：

(S2+P1+P2-S1)cosθ2+T2+2Ts2=(G2+σ-Fs)sinθ2

(2)

(S2+P1+P2-S1)sinθ2+(G2+σ-Fs)cosθ2=N2

(3)

其中：

(4)

(5)

(6)

(7)

Ts2的大小可以根据已知文献[16-17]计算：

(8)

(9)

在极限平衡状态下，滑动力与抗滑力处于静力平衡状态，则：

(10)

联合公式(2)～(10)，可得：

(11)

切割时，水刀切割主要是为了切割桩基，故在切割的过程中桩基逐渐被分割成多快，如图8所示。

因此滑动体外部桩的作用力P1、P2以及滑动体内部桩的摩擦阻力Fs逐渐减小，直至为0，此时若需维持掘进面稳定，支护力由公式(11)变为

(12)

由于水刀与掘进面是非接触形式，故无论是在加固土体还是切割桩基的过程中掘进面上的支护压力均为0，因此加固长度对于维持掘进面的自稳十分重要。根据上述分析，加固长度d的最小值可以通过公式(13)计算出：

(13)

其中，

(14)

(15)

(16)

3 模型验证

3.1 数值模型验证

3.1.1数值模型建立

考虑到尚未有相关的工程实例，为验证所提出理论模型的合理性，本文采用Midas软件先进行前处理，然后导入FLAC3D软件进行计算。共设计4组计算模型，加固长度分别取2，3，4 m及5 m，将结果与理论值进行对比。

考虑到计算效率，根据对称性建立1/2几何模型进行计算，模型尺寸为30 m×30 m×30 m，整体模型单元体总数为75 500个，拟开挖隧道的高度为6 m，隧道埋深比为 2，桩直径 1 m，h1=h2=1 m，计算模型如图9所示。土体采用线弹性模型，并服从Mohr-Coulomb破坏准则，桩采用实体单元进行模拟。模型的顶面设置为自由面，底面设置为固定面，模型两侧只允许产生竖向位移。土体主要参数见表1和表2。桩与非加固区以及加固区土体之间建立接触面，接触面的c与φ值取桩周土参数的0.7倍，法向刚度Kn和切向刚度Ks参数选取依据文献[18]，具体参数见表3。

表1 土体参数Tab.1 Soil parameters

表2 加固区土体参数Tab.2 Soil parameters of reinforcement area

表3 接触面参数Tab.3 Parameters of interface

详细的数值模拟过程如图10所示，根据计算结果作出支护压力与掌子面中心点水平位移的曲线图(见图11)，借鉴确定桩承载力的Q-s曲线方法，来得出掌子面的极限支护压力如图11所示。

3.1.2结果分析

从图11可以看出：在加固长度为2 m和3 m时，掘进面的极限支护压力分别为12.5 kPa和5.5 kPa。将数值模拟值与理论计算值进行对比，见图12，当加固长度为2 m时，理论解和数值解分别是12.5 kPa和12.0 kPa，两者相差4%；当加固长度为3m时，理论解和数值解相差5.5%，最大误差均在10%以内，验证了本文提出理论的合理性。

3.2 工程案例验证

3.1节通过数值分析对公式(11)进行了验证，考虑到公式(12)表示的是桩基障碍物被切割完成之后的支护压力计算公式，所以公式中已经不包含障碍物的相关参数，该公式也适用于采用暗挖隧道施工过程，本节拟采用工程实例对公式(12)的合理性进行验证。

文献[19]以蒙华铁路万荣隧道工程为例，采用数值模拟与工程实际监测相对比的方法，确定了在隧道全断面开挖时采用水平旋喷桩对掌子面进行超前加固，加固长度为3 m时可以维持掌子面的稳定。隧道埋深为20 m，隧道直径为10 m，原状土和加固土的相关参数可以参考文献[19]，这里不再赘述。本节采用 Mathematica软件对公式(12)进行编程计算，得到的结果为S2=-1.29 kPa，可知加固长度为3 m的时候，计算得出的支护压力小于0，为负值，表明此时掘进面可以维持自稳，不需要施加支护力，所得结论与文献[19]相同。

4 参数分析

基于支护压力计算公式(12)，研究加固土体内摩擦角、埋深比以及加固长度等因素对支护压力的影响。以黏土为例(其他土层分析方法相同)，本文假定在桩基距掘进面1 m的时候进行加固，隧道的高度D=6.0 m，滑动体宽度B=6.0 m，未加固区土体重度为18.0 kN/m3，黏聚力为20 kPa，内摩擦角为10°；加固区土体重度为28.0 kN/m3，黏聚力为100 kPa。

4.1 内摩擦角和埋深比对支护压力的影响

本节以加固长度为不变量，以加固土体的内摩擦角和隧道的埋深比为变量，研究两个变量对支护压力的影响规律。各参数的取值如表4所列，计算结果如图13所示。

表4 参数取值Tab.4 Parameters in calculation

由图13可知，当内摩擦角不变时，支护压力随着隧道埋深近似呈线性增加，最多增加了11 kPa。当埋深比不变时，随着内摩擦角的增大，所需的支护压力减小得越明显，最多减小了4.2 kPa。

从图13可以看出：加固长度为2 m、埋深比在1～3之间，加固体的内摩擦角小于35°时掘进面所需要的最小支护压力为0.25 kPa。此时并不能满足水刀切割无支护压力的要求，因此在实际工程中当加固长度被限制时，可以考虑增大加固体的强度，从而增强掘进面的自稳能力。

4.2 内摩擦角和加固长度对支护压力的影响

本节研究加固土体内摩擦角和加固长度对支护压力的影响。由于现在隧道建设的快速发展，大埋深的隧道已经成为一种趋势，故本节选取的隧道埋深比为3，更符合实际情况，桩径暂定为1 m，加固长度分别为2，3，4，5 m，计算结果如图14所示。

从图14可知，当横坐标的内摩擦角保持不变的时候，支护压力与加固长度呈负相关，且当加固长度为4 m和5 m时，支护压力值相差较小，此时的理论计算值均为负值，表明此时的支护压力由“推力”变为了“拉力”，说明掘进面在不施加支护力时可以维持自稳。当加固长度一定时，支护压力随加固土体内摩擦角的增大而减小。

从图14可以进一步看出，当加固长度大于4 m时，土体的内摩擦角在20°～35°之间，掘进面均可以维持自稳。当加固长度为4 m时，将其带入到公式(13)中反算可以得到水刀切割时维持掘进面自稳需要的加固土体最小内摩擦角约为14°。

4.3 埋深比和加固长度对支护压力的影响

本节研究埋深比和加固长度对支护压力的影响。根据目前国内工程使用桩径的情况，确定桩径为1 m，加固区土体的内摩擦角为20°。埋深比H/D分别取为1，2，3，加固长度分别为2，3，4，5 m，计算结果如图15所示。

从图15可以看出，当加固长度一定时，支护压力随着埋深比的增大而增大，当加固长度超过4 m时，支护压力变为负值。当埋深比一定时，支护压力随加固长度的增大而减小。

当加固长度大于4 m之后，掘进面支护压力变为负值，表明掘进面可以维持自稳，实际工程中当加固体的强度不能得到有效保证的情况下，可以通过增大加固长度来维持掘进面的稳定。

4.4 各参数相关性分析

基于上述参数分析得出的数据，采用Spearman相关系数方法来确定输入变量埋深比、内摩擦角、加固长度与输出变量支护压力之间的相关性。各参数间的相关系数见公式(17)。

(17)

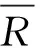
3个输入性变量中埋深比与内摩擦角的相关性较差(ρs<0.5)，埋深比、内摩擦角与加固长度的相关系数为0.51、-0.32，分别呈现正相关和负相关。3个输入变量和输出变量的之间的相关性强弱为：加固长度>内摩擦角>埋深比。

5 结 论

本文介绍了一种新型盾构破除桩基工法——水刀切割工法，并结合极限平衡理论对该工法条件下的盾构掘进面开挖稳定性问题展开了研究，主要结论如下：

(1) 基于水平条分法，考虑桩-土相互作用、上覆荷载、地层强度、加固长度等影响因素，构建出盾构切割情况下的掘进面极限支护压力和超前加固长度计算公式，并通过数值模拟验证其可行性。

(2) 通过参数分析发现支护压力与埋深比呈正相关，与土体内摩擦角、加固长度等参数呈负相关。

(3) 通过参数相关性分析发现埋深比与内摩擦角的相关性较差，3个参数和支护压力之间的相关性强弱为加固长度>内摩擦角>埋深比。