基于改进GRU的电力大数据分析

张明达，崔昊杨，余豪华，孙益辉，王思谨，王浩乾

(1．国网浙江奉化区供电有限公司，浙江 奉化 315500；2．上海电力大学，上海 200090)

从数据的角度揭示电力设备内部状态变化规律，是捕捉故障先兆信息、追溯故障过程、预测故障概率的重要依据。然而，电力设备状态数据不仅来源多，还会由状态监测系统可靠性差、测量失误、设备系统扰动等情况导致不完整、冗余、遗漏、错误等无效异常数据的存在。这些无效、异常数据的出现导致设备状态真实规律难以挖掘，严重者可能导致状态规律挖掘错误。因此，如何避免无效异常值对设备真实规律挖掘的影响，以及如何提高数据挖掘算法的鲁棒性成了电力大数据的核心问题。

目前，电力大数据分析常采用的方法按应用场景可分为：以整合移动平均自回归模型(Autoregressive Integrated Moving Average model，ARIMA)为代表的统计分析，以神经网络(Back Propagation，BP)、支持向量机(Support Vector Machine, SVM)等为代表的智能学习方法，以及以长短期记忆网络(Long Short-Term Memory，LSTM)、门控循环单元(Gated Recurrent Unit，GRU)等为代表的深度智能学习方法。其中，以ARIMA为代表的统计分析方法不需大量样本进行训练，并且具有较高的准确率，但是当数据增大到一定规模后，该类算法容易陷入局部最优(即只反映短期规律，不能反映长期规律)；以BP、SVM为代表的智能学习方法虽然容易训练，但是海量数据处理时存在梯度消失的情况；而以LSTM、GRU等为代表的深度智能学习方法，由于具备长期的“记忆细胞”，可以轻松处理海量数据，并且具有极高的准确率，但是这类方法对数据的有效性、一致性、完整性的要求严苛。由于监测系统产生的无效异常值将破坏LSTM、GRU这类算法的“记忆细胞”，进而导致规律挖掘出错或无法挖掘。

针对当前状态数据存在的问题和现有GRU算法的不足，提出了基于改进GRU的电力大数据分析模型。该模型首先针对状态数据一致性、有效性较差，以及冲击、无效数据影响数据真实性的问题，利用自适应阈值的小波变换对数据进行清洗；其次，以周期为单位将清洗后的数据分为多个数据段，通过对各数据段同一时刻的记忆进行求和，并将求和结果的平均值作为标准记忆，以此消除不完整数据对状态规律挖掘的影响；最后，根据数据段的质量高低对GRU的“记忆”进行更新，即数据质量好的多记，数据质量差的忘记。实验结果表明，提出的预测模型在数据未滤波和滤波后的预测均方根误差(Root Mean Square Error , RMSE)均低于 ARIMA 、LSTM和GRU 模型。

1 电力状态大数据特性分析

状态数据贯穿设备全寿命运行的整个时期，具有总量大(Volume)、增长快(Variability)、密度低(Value)等特点。并且，从图1的光伏发电可知，新能源光伏发电数据以0.25h为单位进行采样，故光伏发电的数据在总量、增长速度方面均比设备状态数据大；此外，由于光伏发电易受气候影响，其价值密度不仅低于状态数据的价值密度，还多了图1中周四光伏发电波动数据的无效异常数据。因此，本文以“迎刃而解”为思路(能挖掘困难的新能源发电数据规律，那也能挖掘较为简单的状态数据规律)，对本文算法的有效性进行验证。同时，为了便于比较，采用RMSE作为评价依据，计算公式如下：

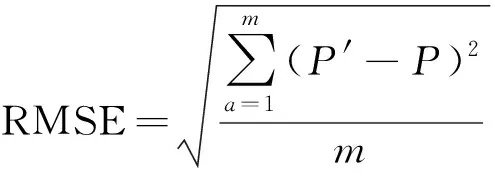
(1)

式中：′、分别为预测数据、现实数据。

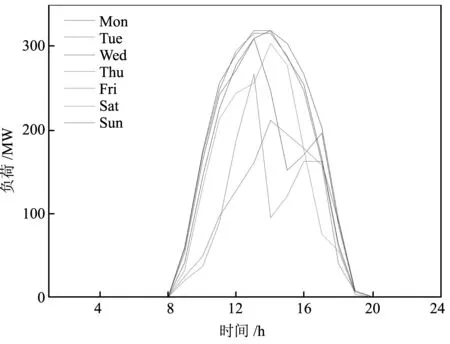
图1 一周内光伏发电的负荷

由于光伏发电都在8之后，于是采用08:00-20:00的发电数据进行预测分析，ARIMA、LSTM、GRU预测准确度如表1所示，预测结果如图2所示。结合表1和图2可知，ARIMA预测准确率最低，RMSE达到了135，而LSTM及LSTM变体GRU的RMSE虽然比ARIMA较小，分别为41和39，但预测准确率依旧有待提高。由此可见，类似周四的异常数据不仅加大了数据规律挖掘的难度，还降低了挖掘算法的准确率。

表1 ARIMA、LSTM、GRU预测光伏发电的负荷与真实值的RMSE对比

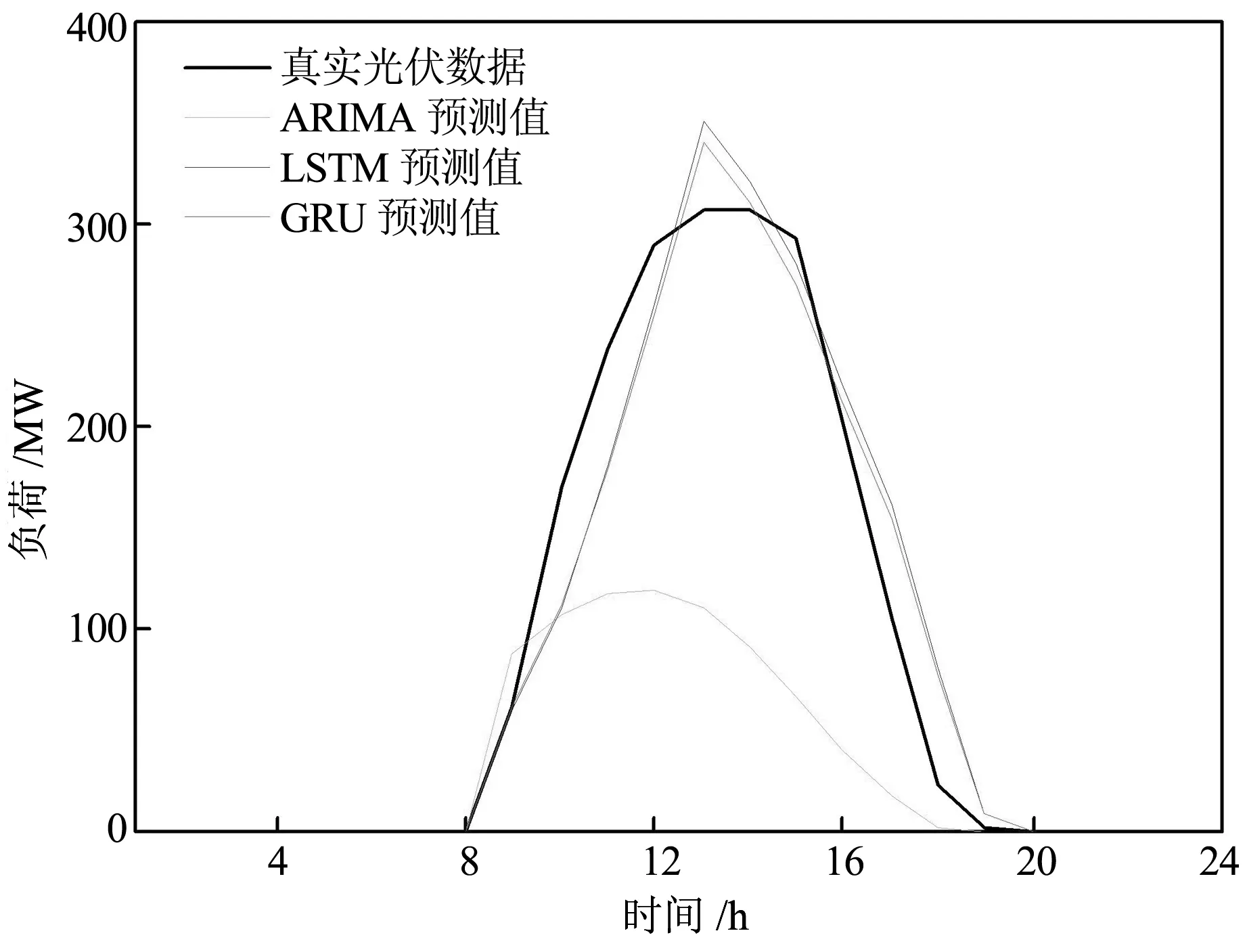
图2 ARIMA、LSTM、GRU预测光伏发电的负荷与真实值的对比

2 基于改进GRU的电力大数据分析

从图1可知，类似周四的数据由于受气候影响，其波动性影响了整天发电数据的规律性，这些无效的异常数据造成当天发电数据呈现出一个假的“驼峰规律”性。因此，针对这些无效、异常数据的影响，以及当前算法的不足，本文通过数据质量改善和算法改进两部分进行改进。

2.1 数据质量提升

针对无效、异常数据的影响，参照文献[12]，利用自适应小波滤波算法进行数据质量提升。传统的小波滤波常用阈值选取公式为：

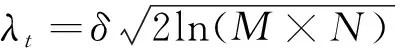
(2)

式中：、和分别为噪声均方差、信号提升层数和信号范围。由于无效异常值的出现是随机不可预知的，无法得到数据和噪声的统计特性先验规律，故针对规律失真的情况，利用数据真实性定义其自适应阈值范围，改进后的自适应阈值小波滤波为：

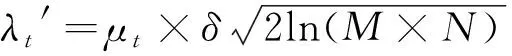
(3)

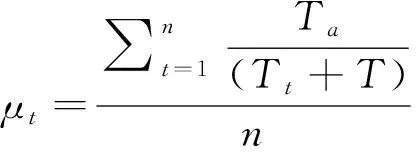
(4)

式中：和分别为当前采样值和上次滤波结果。

2.2 改进GRU模型

作为LSTM改进体的GRU虽然简化了输入和输出，即LSTM的输入、输出、忘记门简化为更新门和重置门，但是依旧保持了LSTM预测准确率高的优点。标准的GRU门控逻辑如图3所示，时刻GRU状态输出为：

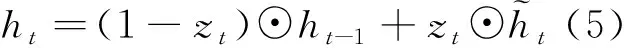
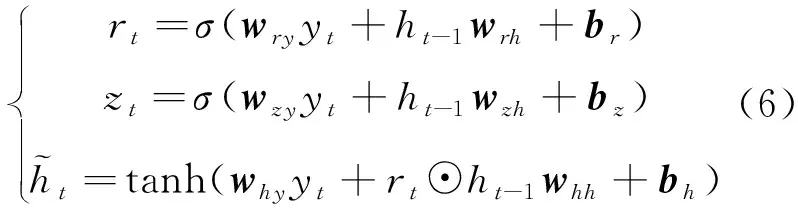
式中：、、和⊙ 分别为Sigmoid激活函数、权重矩阵、偏置向量和数据对应位置的点乘运算。

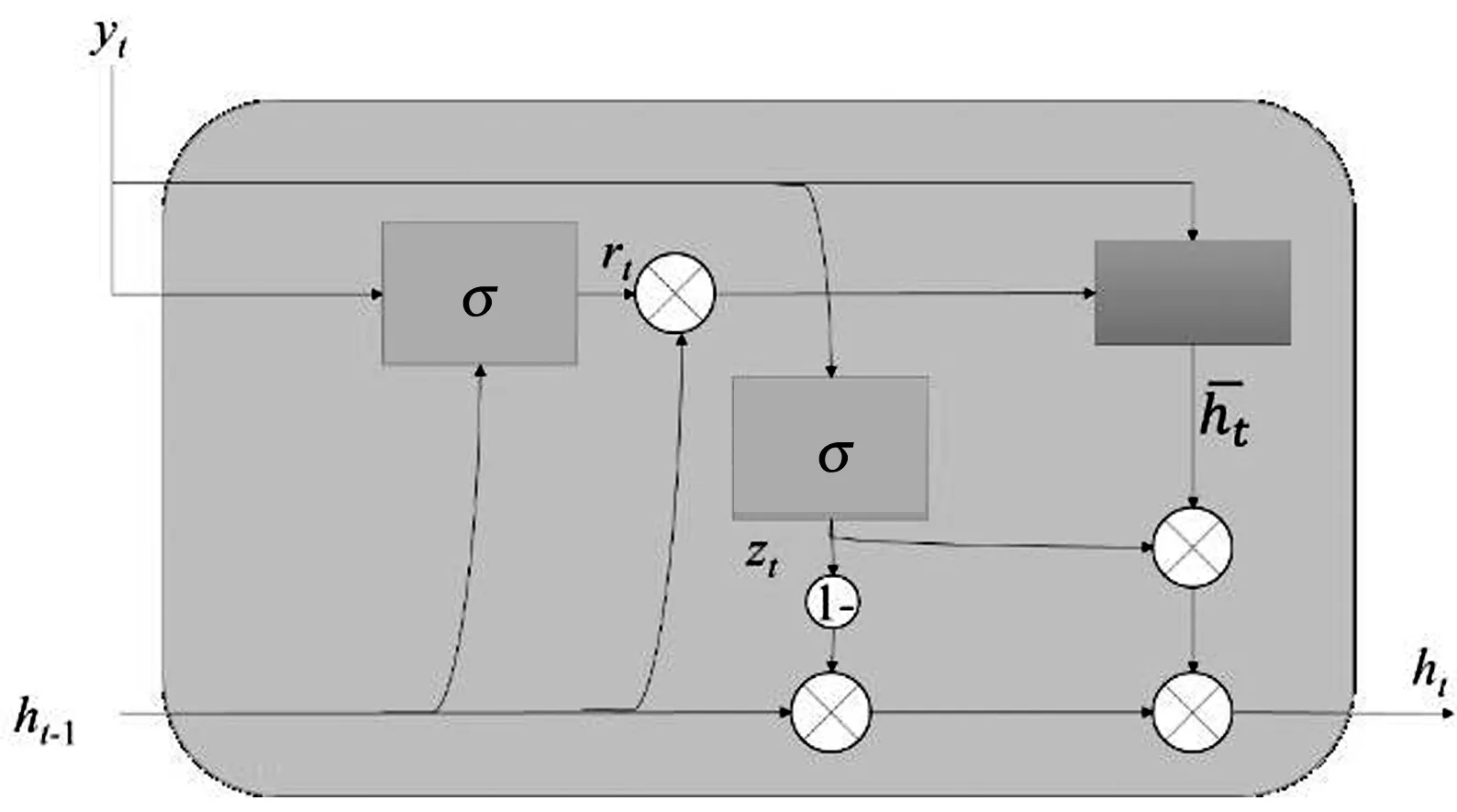
图3 标准的GRU门控逻辑

从图3中GRU的门控逻辑可知，重置门决定了如何将新数据与之前记忆结合，而更新门则决定了多少之前记忆的作用。因此，提高算法对无效异常数据鲁棒性的关键在于如何和。为此，本文对GRU进行改进，改进后的GRU门控逻辑如图4所示。本文根据自适应小波滤波对数据质量提升程度，将数据分为个周期段，将各周期段同一时刻的平均记忆作为标准记忆。利用标准记忆对GRU的重置门进行选择性记忆，即数据质量高的多记忆、数据质量差的少记忆。改进后的GRU为：

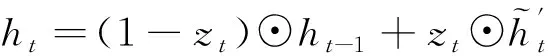
(7)

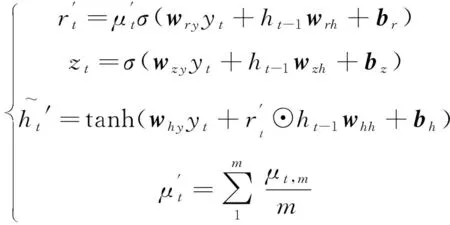
(8)

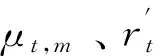
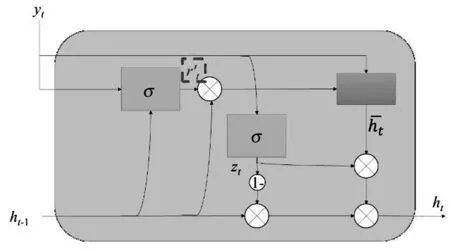
图4 改进后的GRU门控逻辑

3 实验分析

为了验证本文模型在异常、无效数据影响情况下均具有较高的准确率和可靠性，进行了以下实验。实验分为两部分：原始数据情况下不同算法之间对比和数据滤波后不同算法之间对比。从图5和表2的对比中可知，无效异常数据导致的失真规律虽然对GRU的记忆造成了影响，但是本文对重置门进行了选择性记忆，失真较大的规律被遗忘，预测准确率相对于ARIMA、LSTM和GRU分别提高了76%、16%和11%。

另外，经过本文方法滤波后的光伏发电数据的质量得以提升，以周三和周四数据改善结果最为明显，数据上升沿和下降沿的失真得到了抑制。本文模型、ARIMA、LSTM和GRU利用滤波后数据进行预测的准确率相对于未滤波数据预测准确率分别提高了28%、56%、13%、13.8%；利用失真得到抑制的数据进行预测，本文模型预测准确率相对于ARIMA、LSTM和GRU分别提高了61%、30%和25%。

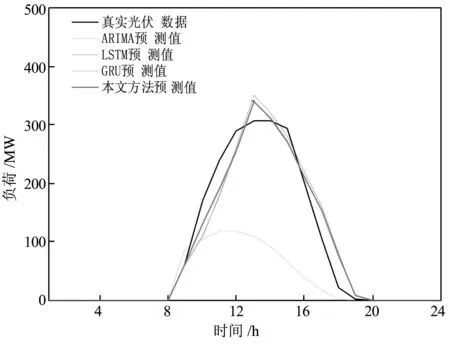
图5 数据未滤波情况下，本文方法与ARIMA、LSTM、GRU预测结果对比

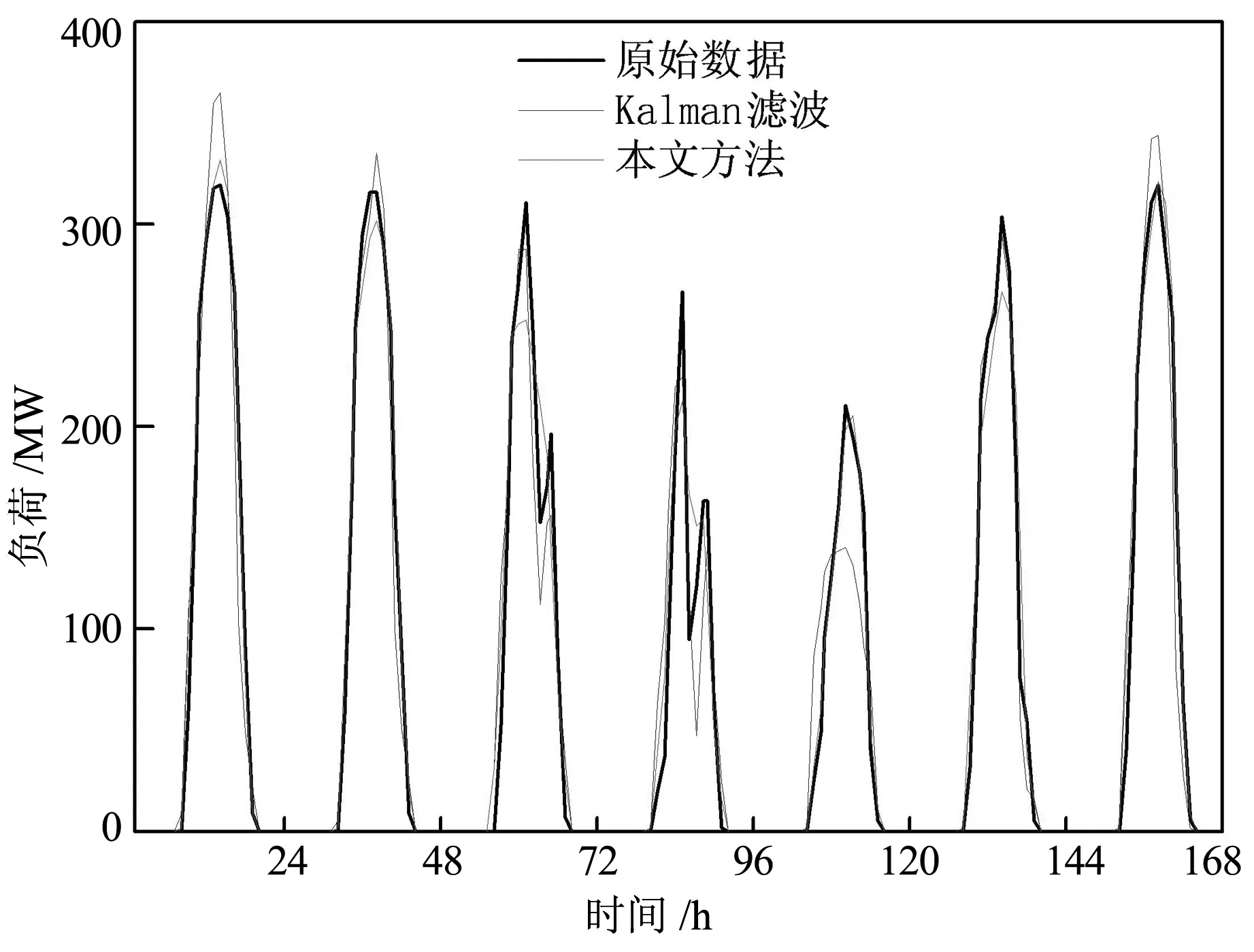
图6 本文方法与Kalman滤波对数据质量提升情况对比

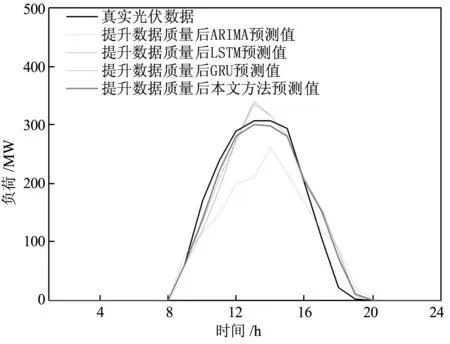
图7 数据滤波后，本文方法与ARIMA、LSTM、GRU预测结果对比

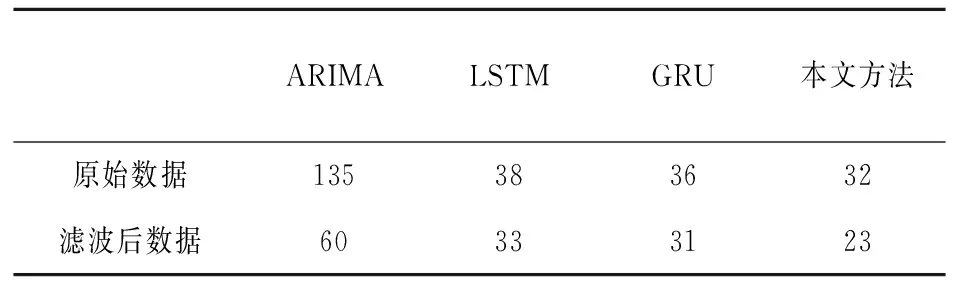
表2 ARIMA、LSTM、GRU和本文方法预测光伏发电的负荷与真实值的RMSE对比

4 结 论

针对电力大数据分析过程中存在无效、异常数据导致数据质量较差，以及当前数据分析方法难以在规律失真情况下分析真实规律的问题，提出了基于改进GRU的调控大数据分析模型。该模型采取自适应小波滤波的方法提高数据质量，降低数据规律失真率；并通过改进GRU的重置门的记忆细胞提高模型抗数据失真鲁棒性。