机器学习下随机森林算法在电网故障分析指挥系统中的应用

汤卫东，肖大军，谈林涛，于文娟

(国家电网有限公司华中分部，湖北 武汉 430077)

随着互联网和信息技术的不断进步，以大数据为依托的机器学习和人工智能成为热门的发展方向，面对大量的数据和信息，对其进行快速的分类并从中找出潜在的规律是机器学习的主要目的，目前，数据挖掘对分类技术的研究已经取得了非常重要的进步，以决策树和深度学习为代表的数据分析模型不仅操作简单而且效果显著。

随着人们的生活质量不断提高，对于数据处理的需求也越来越高。由于神经网络在连续处理大量数据的过程中容易产生过度拟合的问题，同时对于数据样本的要求也比较高，所以在许多领域都有非常广泛的应用。但程中还存在局限性。在这样的背景下，以决策树为核心的多分类随机森林算法(Random Forest Algorithm, RFA) 得到了研究学者的关注，作为一种典型的多分类器算法，随机森林可以很好地对数据进行集成学习，同时根据数据的多样性进行分类处理，避免了神经网络对数据的过度拟合，因此随机森林算法拥有非常强大的适用性，可以在许多领域进行广泛应用，特别是针对一些非线性高维数据，随机森林算法也可以很快地进行处理，此外，随机森林算法对噪声和随机误差的防控非常到位，可以极大地减少因数据产生的误差，从而降低了数据处理难度，节约了大量的人力物力，帮助数据得到快速、准确的分析。

基于大数据时代背景，通过阅读和查找大量的相关文献和资料对电网系统的故障分析进行评级，然后利用随机森林算法的决策树分类模型对电网系统的故障进行预测分析，将随机森林算法与其他应用较广泛的算法的预测准确率进行对比验证随机森林算法的实用性和优越性，然后在Weka平台上利用当地电力局的数据样本进行仿真模拟，对电网故障的预测准确率结果进行分析，验证故障分析模型的科学性和准确性。对于电网系统的故障预测具有非常重要的指导意义。

1 机器学习下的电网故障分析

1.1 电网故障分析原理简述

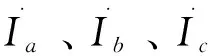
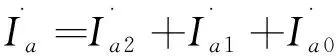
(1)

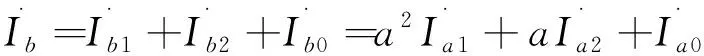
(2)

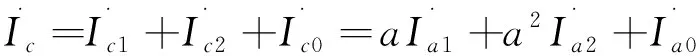
(3)

解方程(1)-(3)可得：

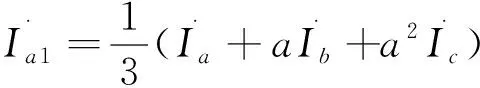
(4)

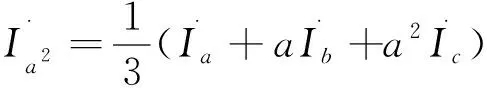
(5)

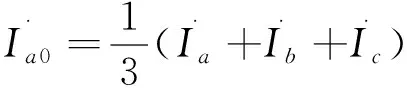
(6)

将其表示为矩阵的形式：

=

(7)

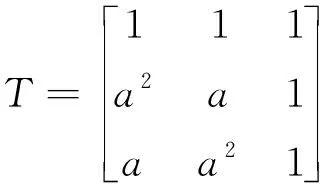
(8)

最后对电压进行变换：

=

(9)

此外，对称电路故障主要是根据电源三相系统进行分析,因为发生短路前后，电源的电压和频率不会发生变化，所以设短路前的电压和电流分别为、：

=sin(+)

(10)

=sin(+-)

(11)

其中相电流的有效值为：

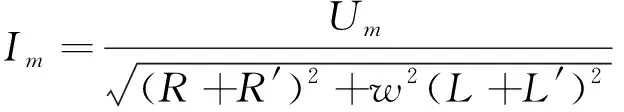
(12)

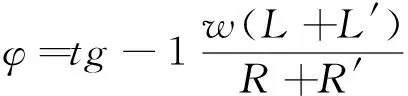
(13)

其中，和分别为每相电路的电阻和电感，当电路发生短路后，a相的电流表达式可表示为：

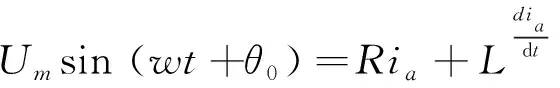
(14)

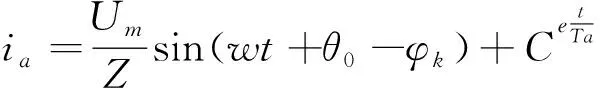
(15)

当电网系统发生故障时，工作人员必须及时对故障进行排查，确定故障来源和故障所在区域，利用对称故障和非对称故障法可以快速地实现对故障的定性处理，通过电压、电流及其他参数的变化来确定故障类型，从而帮助电网系统解决故障，恢复电路正常运行，保障居民的用电需求。

1.2 机器学习和随机森林算法

机器学习(Machine Learning)是利用计算机模拟人类大脑学习过程的一种多学科交叉理论，信息时代，对数据信息进行筛选和处理,是当下研究的热点话题。机器学习领域广泛，可以完成大量数据的快速分类和处理，实现数据预测和分析。

随机森林算法是机器学习领域中一种普适性良好的数据挖掘方法。其运行原理是在决策树算法的理论之上结合 boot strap 重采样方法，集合多个单树型分类器，最后结果通过投票的策略进行分类和预测。随机森林算法具有多重优点，调整参数较少，抗噪声能力强，最重要的是在实际的应用中分类性高，不容易发生过拟合等。但也有其缺点，随机森林算法的特征选择具有随意性，导致忽略特征对类别的重要性以及特征与特征之间的相关性，采用重抽样技术通过随机抽取样本形成新的训练集，然后利用自主数据集进行决策树建模，并组成随机森林，分类结果进行投票决策。随机森林的数学定义如下：首先设置一系列的决策()、()、…,()构建森林，同时随机取两个向量、，则边缘函数为：

(,)=((()=)-

max((()=)

(16)

=,((,)<0)

(17)

其中为正确的分类分量，为错误的分类向量，表示取平均值，表示泛化误差，边缘函数的值越大，说明该模型的可信度越高。而随机森林的边缘函数为：

(,)=(()=)-

max(()=)

(18)

其中，(()=)表示判断正确的分类概率，(()=)为判断错误的分类概率。

随机森林算法主要运用于数据分类和预测中，根据数据集中元素的特点可以分为正类和负类，和分别表示正确分类中正类和负类的样本数量，而和分别表示错误分类中正类和负类的样本数量，则随机森林算法的分类精确度为：

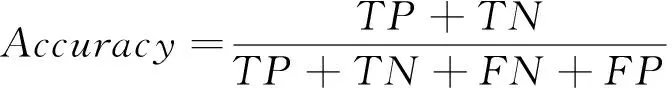
(19)

精确度越高说明其分类效果越好，此外，灵敏度和特异度的定义分别为：

=+

(20)

=+

(21)

其中灵敏度表示随机森林对正类数据的分类精度，特异度表示对负类数据法分类精度。随机森林的设计总原则是要保证灵敏度和特异度的平衡性，也就是两者总体均值的最大化，评价指标为几何均值-：

-=

(22)

最后，负类数据对应的三个评价指标为查全率和查准率以及负类检验值：

=+

(23)

=+

(24)

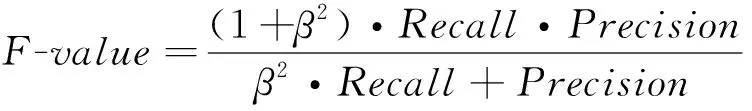
(25)

其中，查全率表示正确分类中的负类样本在全部负样本中的比例，查准率表示正确分类的负类样本在所有预测为负类样本中的比例，而负类检验值-是随机森林算法中一个综合的评价指标。随机森林算法的示意图如图1所示：

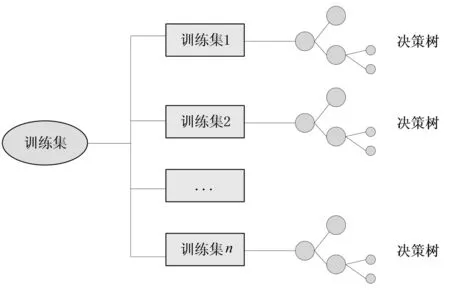
图1 随机森林算法示意图

2 基于随机森林算法的电网故障分析模型

实验对象：当地电力局的供电系统，以输电网络为主要分析对象，利用数据挖掘技术查找近三年的电网故障发生的时间和故障原因，并进行收集整理。

实验数据来源：采取数据挖掘技术对当地电力局近三年的输电数据进行收集，以2019年到2020年的数据作为训练样本，以2021年1月的数据作为测试样本数据，2-3月的数据作为预测样本。其中按照每个月的输电故障为标准，每个月的故障次数在2次及以内为正常，评级为1；故障次数在3-6次评评级2,故障次数在7以上为故障高峰，评级为3。

实验环境：随机森林算法使用randomForest4.6语言软件来实现，主要参数设置为：决策树的数量为1000，随机属性的个数为3。在Weka数据挖掘平台上建立电网故障分析模型，对比不同算法对电网故障的分析效果和精确度。

3 实验结果分析

3.1 不同算法的对比分析

引入决策树(decision tree)算法的一种(C4.5)、神经网络算法(Neural Network Algorithm, NNA)以及支持向量机(Support Vector Machines)算法和随机森林算法(RFA)进行对比，预测准确率和统计值指标如图2所示。

由图2可知，随机森林算法的预测准确率和统计值指标要明显高于其他三种算法，准确率高达93%，而其他三种算法的准确率均在90%以下，随机森林算法的优越性得到了验证。随机森林算法决策树的随机性使数据多样性得到提高，使环境和人为因素引入的误差相对降低，避免了数据过度拟合的问题，增强模型的普适性。

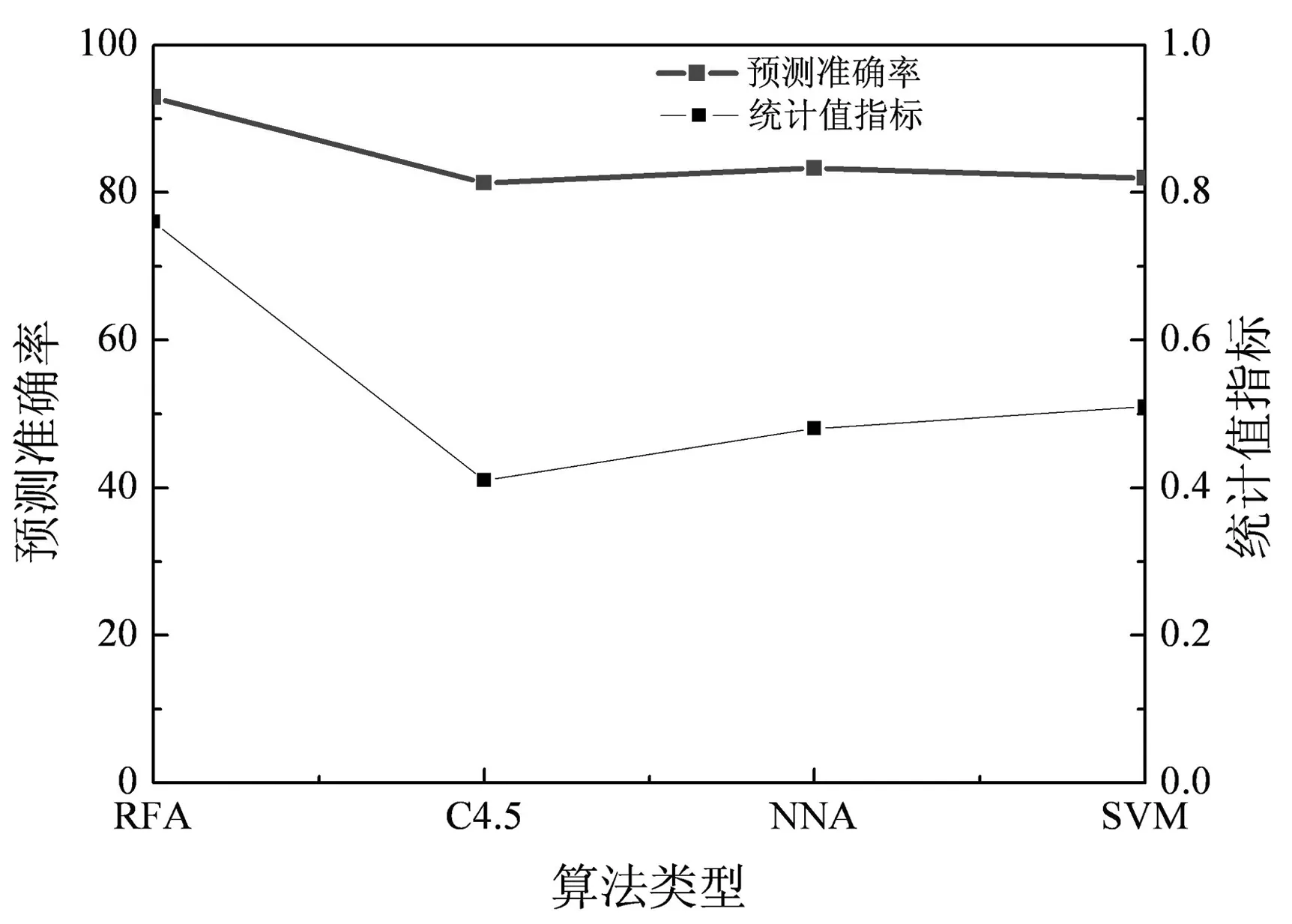
图2 不同算法下电网故障的预测准确率与统计指标

3.2 电网故障的预测分析

利用随机森林算法的电网故障分析模型进行检测，不同故障等级的样本数量对比如图3所示。

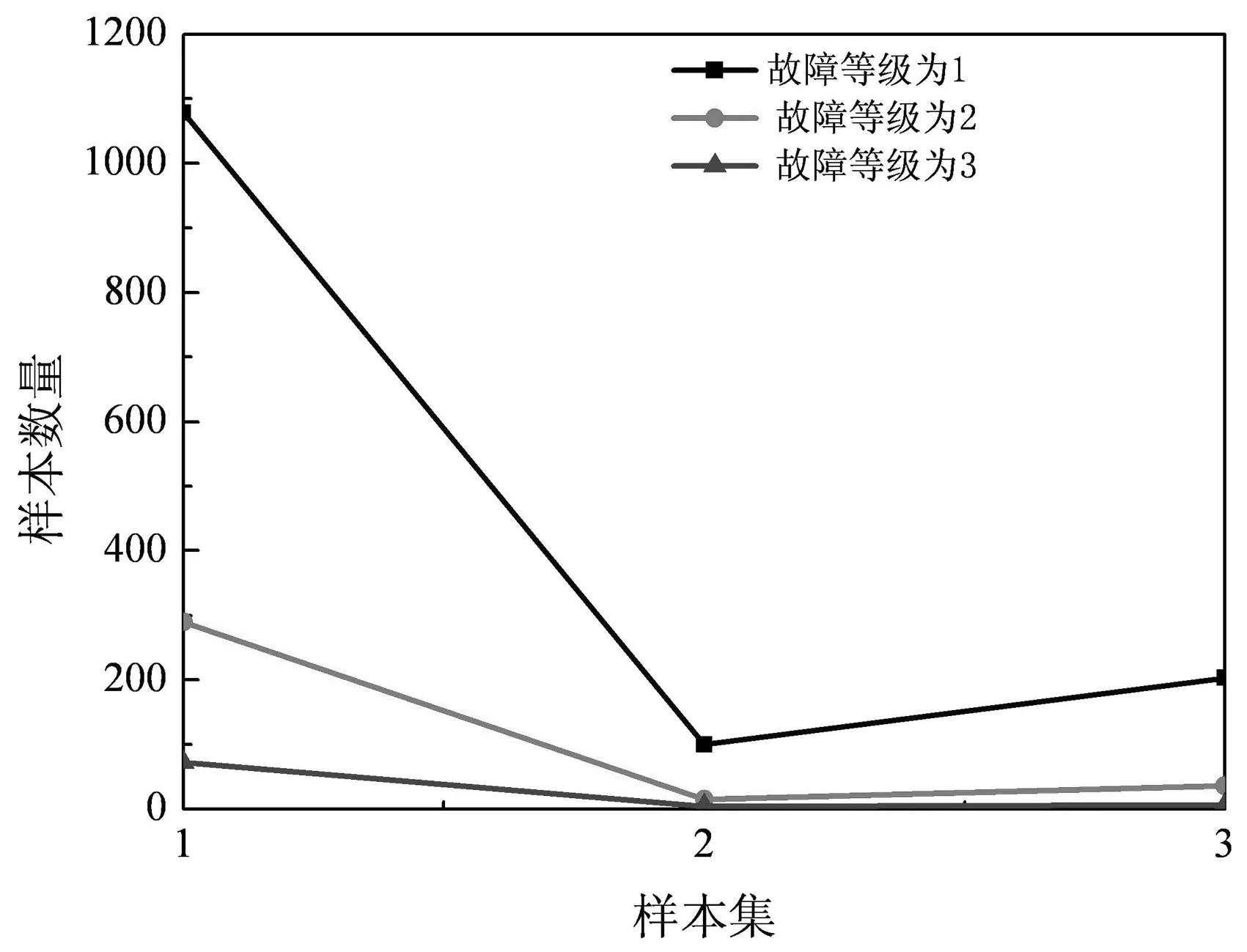
图3 不同故障等级的样本数量(横坐标1-3分别表示训练样本、测试样本、预测样本)

由图3可知，训练样本的数量要远远高于测试样本和预测样本的数量，同时故障等级为1的样本数量远远超过其他两个，说明该电力局的电网系统相对比较安全，故障发生的概率较低。

根据预测样本的故障等级和实际故障对比，电网故障的预测结果如图4所示。

由图4所示，电网故障分析模型在2月和3月的预测中，总的预测准确率分别为95%和96.8%，其中等级为1的故障准确率均在95%以上，而故障等级为2的准确率为70%和89%，等级为3的预测准确率为66%和100%，这是由于样本数量较少，容易出现随机误差从而导致准确率降低。整体而言，故障等级越高其预测难度越大，相对准确率也较不稳定，而故障等级越低，预测准确率越高。

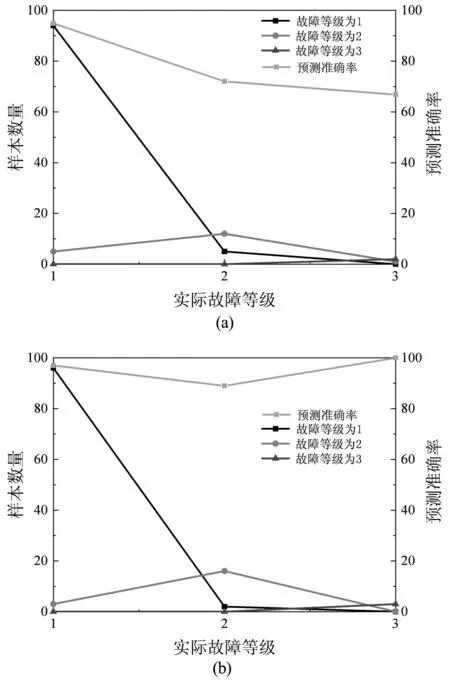
图4 电网故障的预测结果

4 结 论

基于机器学习背景，首先对电网故障的原理展开分析，介绍了机器学习和随机森林算法，根据电网故障的特点利用随机森林算法对电网故障的等级进行分析预测。并引入决策树算法(C4.5)、NNA神经网络和SVM算法作为对照组检验随机森林算法的预测性能，并利用随机森林算法在Weka平台软件上对当地电力局近期的电力故障进行预测。结果表明，随机森林算法的预测准确率和统计值指标要明显高于其他三种算法，准确率高达93%。故障等级为1的预测准确率在95%以上，等级为3故障的预测准确率不稳定，最低仅为66%，相对准确率也较不稳定，故障等级越低，预测难度越低，准确率越高。由于受到客观因素的限制，本研究存在一些局限，在收集数据时未进行预处理，可能存在虚假数据和无效数据，对实验的准确性造成影响。在后续的研究过程中需要对数据进行预处理，提高研究结果的说服力。