基于数字图像相关技术的材料真应力-应变计算与试验*
□ 刘鸿超 □ 周刚毅 □ 付应乾
1.宁波大学 冲击与安全工程教育部重点实验室 浙江宁波 315211 2.宁波大学 机械工程与力学学院 浙江宁波 315211
1 应力-应变关系概述
应力-应变关系是评估材料力学性能的重要依据,对工艺流程、结构设计、仿真模拟的准确性等而言,都至关重要[1-2]。应力-应变关系的计算与处理至今仍然存在一些争议,特别是对于塑性材料,测试过程中会发生次级的几何变化,对计算造成影响。对此,学者们进行了许多试验,对承受不同载荷的工程材料进行机械测试,具体包括拉伸[3]、压缩[4]、剪切[5]、扭转[6]、缺口拉伸[7]等,用于测试材料的应力-应变关系。上述方法中,大部分仅在应变小于0.5时可以获得真正的应力-应变关系,然而在锻造、挤压、轧制等金属成型中,最大应变通常超过1.0,在多级自动冷锻中,应变可以达到3.0。拉伸试验是材料力学性能测试中最常见的试验类型[8],通过拉伸试验,可以获得材料的拉伸强度、屈服强度、屈服点、弹性模量、伸长率百分比、面积减小百分比等主要参数。但是,拉伸试验同样也很难获得超过拉伸强度,即颈缩应变后大应变下材料的真应力-应变曲线。为了评估材料裂纹尖端或壁薄部分的韧性断裂,包括颈缩后应变在内的真应力-应变曲线是必不可少的。
真应力-应变曲线对于研究材料机械性能具有重要意义,在文献中只能检索到有限关于真应力-应变曲线的信息,大多数模拟仿真所使用的软件提供的材料特性也没有完全得到验证[9]。笔者基于数字图像相关技术,提出一种处理扁平哑铃型拉伸试样局部真应力-应变曲线的新方法,并通过设计拉伸试验对计算结果进行验证。
2 真应力-应变计算
在处理拉伸试验数据时,试样的工程应力利用拉伸试验机的力传感器所记录的试样两端力-时间信号除以试样初始横截面积得到,试样的工程应变由试样伸长量除以初始长度得到,即:
(1)
εE(t)=ΔL(t)/L0
(2)
式中:σE(t)为试样工程应力;εE(t)为试样工程应变;t为时间;F(t)为t时间试样两端的力;A0为试样拉伸标段初始横截面积;w0为试样拉伸标段初始宽度;h0为试样拉伸标段初始厚度;ΔL(t)为t时间试样伸长量;L0为试样拉伸标段初始长度。
由于试样两端采用夹具固定,拉伸试验机给出的位移与试样拉伸标段的实际变形位移存在误差,因此通常采用高速相机记录试样变形图像,结合二维数字图像相关技术给出试样拉伸标段的位移及应变场。
然而,在拉伸加载超过材料弹性极限后,试样的长度和横截面积是时刻变化的,因此上述计算式计算得到的工程应力-应变并不能代表试样真实力学状态和本构特性。结合应力、应变的定义,可以得出真应力、真应变计算式[10]:
(3)
(4)
式中:σt(t)为试样真应力;εt(t)为试样真应变;A(t)为t时间试样横截面积。
通过式(3)、式(4)可以将颈缩出现之前的工程应力-应变计算转换为真应力-应变,因为在颈缩形成之前,整个试样上的变形是均匀的,在颈缩形成之后,所有后续变形都发生在颈缩区域,颈部横截面积逐渐减小,应变在试样长度方向不均匀分布,导致试样局部真应力与真应变不断增大,直至试样失效,由此,采用式(3)、式(4)计算大应变下的真应力-应变曲线是没有意义的。后文将式(3)、式(4)计算结果称为平均真应力-应变。
图像处理技术是未来重要的一个发展方向[11],其中,数字图像相关是一种借助于对相机拍摄的物体变形前后的表面图像进行计算,分析灰度信息相关性,获取被测物体力学性能,直接提供亚像素精度全场位移和全场应变的技术[12-13]。笔者基于数字图像相关技术,提出一种计算试样不同位置真应力-应变曲线的方法。
对于扁平拉伸试样,任意时间真应力的定义为对应时间的拉力除以对应时间的受力面积,即:
(5)
式中:σT(t)为t时间试样真应力;A(t)为t时间试样横截面积;w(t)为t时间试样宽度;h(t)为t时间试样厚度。
如图1所示,在试样拉伸标段内任意取一个截面A-A,在截面上下取微段dl(0),则初始时刻所选微段的体积V(0)为:
V(0)=w0h0dl(0)
(6)
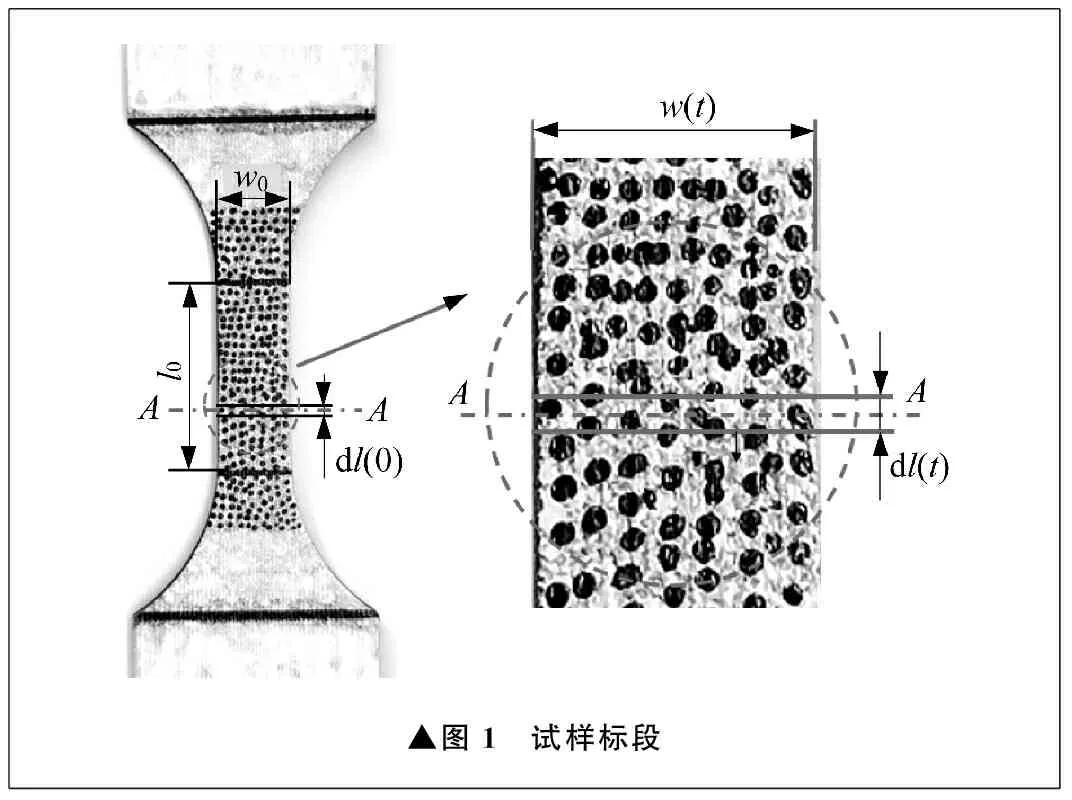
▲图1 试样标段
假设试样任意一个截面厚度的变形是均匀的,由于塑性变形过程中材料体积不变,因此t时间微段的体积V(t)为:
V(t)=w(t)h(t)dl(t)=V(0)
(7)
式中:dl(t)为试样拉伸变形过程t时间微段的长度。
试样截面处横截面积A(t)为:
A(t)=w(t)h(t)=w0h0dl(0)/dl(t)
(8)
将式(8)代入式(5),得到试样截面处t时间真应力为:
(9)
由此可见,只需要通过数字图像相关得到试样拉伸过程任意截面处微段长度的变化信息,就可以方便地得到该截面处的真实应力大小。试验中,利用高速相机记录试样表面变形,结合数字图像相关位移分析,得到任意截面处微段长度的演化过程。对于试样任意截面处的真应变,在数字图像相关全场应变分析中将该截面中点处应变分析结果导出,便可以得到试样任意位置处的真应力-应变。
3 试验验证
3.1 试验材料
试验材料由TA2钛合金冷轧退火板切割成型,成分中,钛不低于99.6%,碳为0.021%,铁为0.064%,氮为0.025%,氢为0.004%,氧为0.11%,其它元素不高于0.18%,材料金相如图2所示,属于平均尺寸约为20 μm的α等轴晶组织。

▲图2 材料金相
3.2 试样
采用哑铃型平板拉伸试样,线切割取样,经精磨加工,表面粗糙度Ra达到3.2 μm,以减小加工表面对试验结果的影响。对试样拉伸标段喷涂人工散斑,以便采用数字图像相关技术进行试样变形过程的全场位移、应变分析。试样如图3所示,试样尺寸如图4所示,试样厚度为2 mm。

▲图3 试样
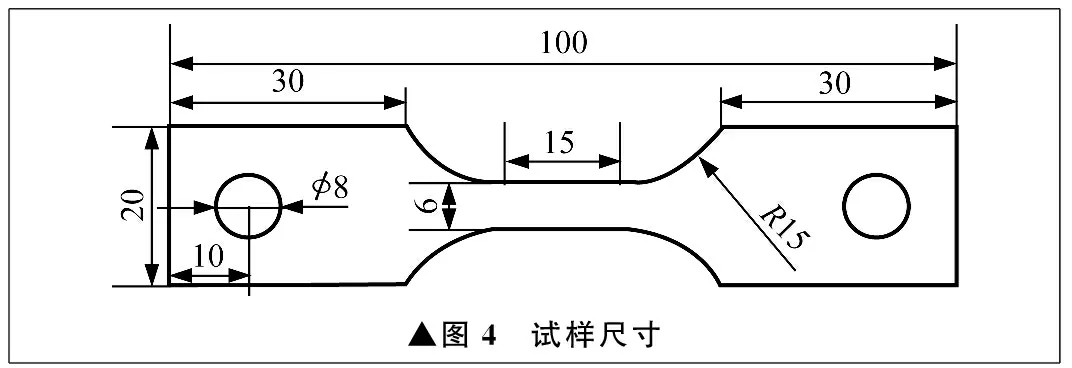
▲图4 试样尺寸
3.3 试验过程
拉伸试验是评估金属材料性能最普遍的试验方法之一。笔者采用HTM-5020液压伺服高速拉伸试验机作为动态单轴拉伸试验的加载设备,并结合高速相机对试样拉伸过程的变形与位移进行记录。试验设备如图5所示。

▲图5 试验设备
HTM-5020拉伸试验机的最高加载速度可达20 m/s,最大可承受拉伸荷载为50 kN,能够精准测试加载过程中的速度与载荷。拉伸试验机通过控制拉伸速度,达到所需要的加载,通过在计算机控制端输入不同的拉伸速度,可以对安装好的试样进行不同应变率加载下的拉伸试验。本次拉伸试验时,拉伸速度为150 mm/s。理论上,试样拉伸的平均应变率为10 s-1。另一方面,为了保证力-变形数据采集的同步性,采用同步触发和数据同步采集装置,使拉伸试验机加载起始时刻同步触发拉伸试验机的力、位移传感器和高速相机,对各传感器信号和图像进行同步采集。
3.4 试验结果
通过数字图像相关技术可以对试样进行全场位移与应变分析,试样拉伸标段应变演化云图如图6所示。由图6可知,开始拉伸加载后,试样拉伸标段内应变开始均匀增大,在工程应变增大到0.124左右后,应变开始不均匀化发展,进一步加载,试样逐渐颈缩破坏。

▲图6 试样拉伸标段应变演化云图
在试样拉伸断裂点P1处截取一个微段,再沿拉伸方向在P2、P3处分别截取一个微段,如图7所示。微段初始长度为0.38 mm。通过数字图像相关技术分析处理,可以得到微段长度的变化。结合应变分析和所采集的力信号,即可计算得到试样拉伸加载过程中的应力-应变曲线。试样应力-应变曲线如图8所示。图8中的平均真应力-应变曲线由式(3)、式(4)计算得到。工程应力-应变曲线在早期便与真应力-应变曲线分离,仅能代表弹性加载段的平均应力与应变,不能很好反映试样拉伸过程中的真实力学状态。采用式(3)、式(4)计算得到的平均真应力-应变曲线在应变约为0.21之前与P1、P2处的真应力-应变曲线具有较高的重合度,P3处的真应力-应变曲线在应变约为0.12时开始与P1、P2处的真应力-应变曲线分离,可见平均真应力-应变曲线只能近似反映试样某个位置的应力与应变情况,且该位置介于P2和P3之间。平均真应力-应变曲线更加适合反映试样拉伸加载前期均匀变形阶段材料的机械性能。采用微段法计算得到的试样不同位置处的真应力-应变曲线在加载前期小应变时具有较高的重复性,反映了相同的应力和应变情况。随着试样不均匀变形,试样不同位置处的真应力-应变曲线呈现出不同变化趋势,反映不同位置处材料的真实力学状态,并且可以有效计算颈缩后大应变变形情况下试样不同位置的真应力-应变曲线。

▲图7 微段位置
4 结束语
笔者基于数字图像相关技术提出一种处理拉伸试样局部真应力-应变曲线的新方法,通过设计拉伸试验对计算结果进行验证。结果表明,工程应力-应变曲线仅能代表试样弹性加载段的平均应力与应变,传统计算方法得到的平均真应力-应变曲线只能近似反映试样某个位置处的应力与应变情况,更适合反映材料均匀塑性变形阶段的机械性能。笔者提出的方法可以有效、合理地计算得到拉伸过程中试样不同位置处的真应力与真应变,包括颈缩后大应变变形下的真应力与真应变,能够反映材料从加载到断裂破坏过程中不同位置的机械性能。
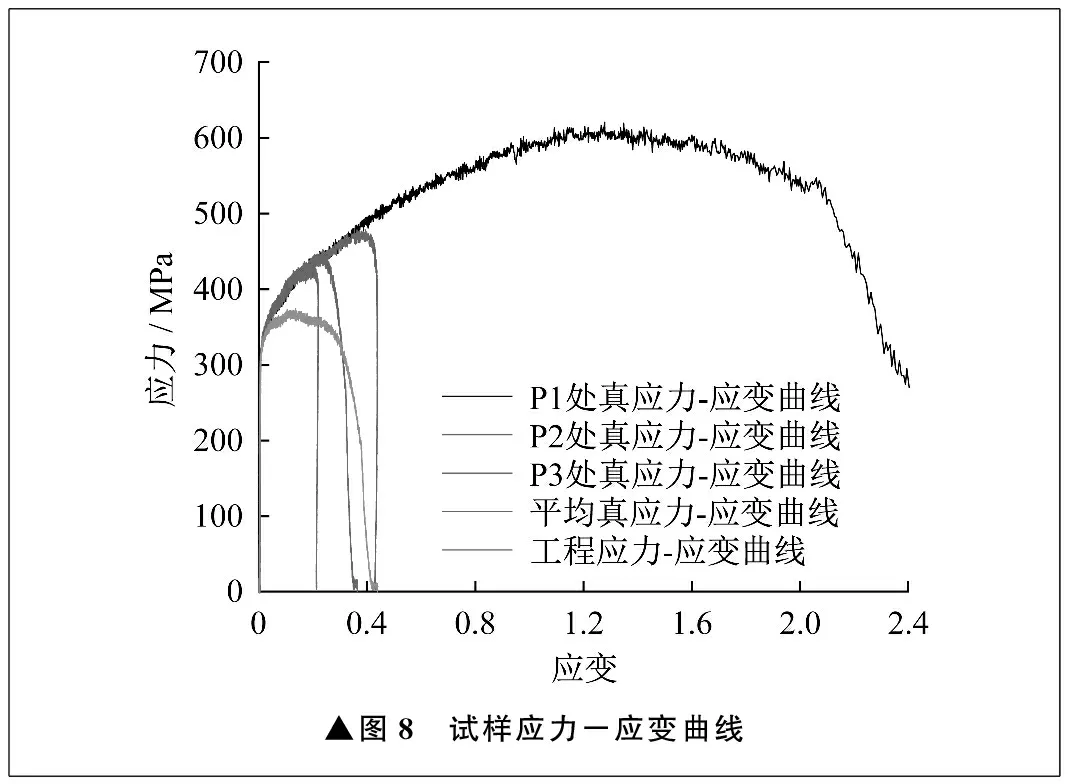
▲图8 试样应力-应变曲线

