基于贝叶斯算法的铣削工艺参数配置优化方法*
□ 张志强 □ 张为民,2 □ 薛 峰 □ 陈圣华□ 马 瑞 □ 赵东方
1.同济大学 机械与能源工程学院 上海 201804 2.同济大学 先进制造技术中心 上海 201804 3.台达电子工业股份有限公司 台北 114501 4.台达智能科技(北京)有限公司 北京 100026
1 研究背景
先进制造技术是当前我国制造业的重点发展方向之一[1]。工艺参数优化是提升机床加工性能,提高先进制造技术的重要途径。工艺参数的选取直接影响机床加工的能耗、质量、效率、成本和刀具寿命等。金属铣削工艺具有复杂性与多变性特点,性能指标等优化目标的具体表达式及其梯度信息难以获得,无法利用优化目标的自身特性和工艺参数的梯度信息来求得全局最优解,并且往往需要花费高额代价才能观测到优化目标的返回值,这些都给工艺参数配置的寻优带来困难。
目前,工艺参数的优化方法主要有两类。第一类是试验设计结合统计分析的方法。Das等[2]利用灰色模糊关联度分析法将多目标优化问题转变为单目标优化问题,并通过田口法试验设计结合方差分析得到最终优化结果。Ahmed等[3]以表面粗糙度和能耗为优化目标,对比田口信噪比分析优化方法和人工神经网络多目标遗传算法的优化效果,验证两类方法的可行性。Camposeco-Negrete[4]采用正交试验、信噪比、方差分析研究粗车加工参数的优化问题。Yan Jihong等[5]提出一种基于加权灰色关联分析和响应面法的多目标优化方法,用于优化铣削过程中的参数。第一类方法避开对优化目标表达式的求解,但是需要采集大量试验数据,并进行统计分析,存在分析过程复杂、优化周期长、优化成本高的缺点,特别是随着待优化因素数量的增加,试验次数会不可避免地大幅增加。另一方面,第一类方法的优化结果只能在事先设定的参数组合中取得,往往不能获得全局最优解。第二类是预测模型结合优化算法的方法。Parmar等[6]将人工神经网络与多目标遗传算法相结合,用于端铣过程的多目标参数优化。Lin Wenwen等[7]利用回归分析建立预测模型,以加工系统碳排放为优化目标,使用教与学优化算法解出帕累托集,并且通过层次分析法得到最优加工参数。Santhanakrishnan等[8]利用响应面法建立预测模型,以端铣加工温升为优化目标,使用遗传算法优化工艺参数。Zhou Jinhua等[9]利用径向基函数神经网络建立预测模型,以表面粗糙度和残余压应力为优化目标,使用粒子群算法优化多轴球头铣削工艺参数。第二类方法通过经验公式、回归分析或机器学习中的回归算法建立从输入到输出的预测模型,易于使用。但是,第二类方法也存在一些问题,如经验公式大多在有限的影响因素下提出,不适用于各类异构、变化加工场景,回归分析及机器学习模型训练需要大量训练数据的支撑。另一方面,使用搜索优化算法的同时即会引入众多待调节的内置超参数,不合适的超参数组合会降低算法效率和准确性,反而提高参数寻优的难度,造成优化方法灵活性差、效果欠理想、效率较低等问题。
贝叶斯算法是一种高效的优化算法,通过设计合适的概率代理模型和采集函数,引入待优化目标完整的历史先验知识,只需要经过较少次数的优化目标评价试验,即可输出良好的优化结果[10]。贝叶斯算法在面对多决策变量,目标函数表达式未知、非凸、多峰,评估代价高昂的黑箱优化问题时,已经取得了优良的效果。Liang Xiao[11]通过卷积神经网络进行灾后桥梁检测,并应用贝叶斯算法对卷积神经网络自身的众多模型参数进行选择。Wang Dong等[12]提出基于贝叶斯算法的支持向量机短期交通流预测方法。Stuke等[13]对比网格搜索、随机搜索、贝叶斯算法在基于核岭回归的机器学习中超参数寻优的效果,验证贝叶斯算法的高效性。Nguyen等[14]在金刚石刀具车削聚碳酸酯表面粗糙度预测研究中对比多种模型的回归效果,验证基于贝叶斯算法的Xgboost模型的优越性。Alajmi等[15]提出基于贝叶斯算法的支持向量机方法,对709M40合金钢常规铣削过程中刀具的磨损优化问题进行研究。Maier等[16]将贝叶斯算法直接应用于车削加工多目标优化的研究中,并证明这一方法的灵活性。从以上介绍可以看到,当前贝叶斯算法正应用于越来越多的领域,其中多数为优化其它模型的超参数,很少直接用于机械加工领域的参数优化。
笔者针对金属铣削加工工艺参数寻优问题复杂多变的场景特点,将其视为黑盒优化问题,以自制样件的铣削加工过程为例,基于贝叶斯算法开展优化应用研究。设计待优化因素及待采集指标,对多个子目标进行基于层次分析法的归一化,以避免多对多预测模型建模的复杂过程。通过贝叶斯算法逐轮进行试验,以完成参数寻优过程,实现工艺参数的快速准确优化。与此同时,基于田口正交试验法进行工艺参数优化试验,并将结果与贝叶斯算法优化结果进行对比,验证贝叶斯算法的寻优效果更佳,寻优试验次数更少,为单次试验成本高昂的金属铣削加工场景提供一种低成本的实用工艺参数配置寻优方法。
2 贝叶斯算法原理
2.1 概述
贝叶斯算法是一种基于贝叶斯定理,以近似逼近为基本思想的参数优化方法,由多种可用的概率代理模型来拟合优化变量与优化目标之间的关系,通过采集函数选择有希望的参数组合进行迭代,最终得出效果最佳的参数组合。理论证明,在最优化采集函数的前提下,贝叶斯算法能够保证最终收敛[10]。
贝叶斯算法模型由五部分组成。
(1) 优化目标。即期望最优化的内容,通常通过评价函数或试验获取优化目标取值。
(2) 优化空间。即优化变量的取值范围。优化空间的设置会影响优化效率和最终优化效果。
(3) 优化变量。即用于调控以获取最优的优化目标取值的变量。
(4) 概率代理模型。用于代替优化变量与优化目标之间复杂的非线性映射关系,这种映射关系通常未知且难以获取。
(5) 采集函数。即用于选取下一组优化变量的依据,一般通过最值化采集函数来选择下一个最有潜力的评价点。
其中,概率代理模型与采集函数是贝叶斯算法的核心。
2.2 概率代理模型
贝叶斯算法利用概率代理模型代替未知的黑箱函数,在概率代理模型中引入先验知识,以减少非必需的优化目标评价。概率代理模型分为参数模型和非参数模型。参数模型有贝塔-伯努利模型、线性模型、广义线性模型等,非参数模型有高斯过程回归模型、随机森林回归模型等。非参数模型具有更高的灵活性,使贝叶斯算法不易发生过拟合问题,其中应用最广泛的是高斯过程回归模型。
2.2.1 高斯分布
对于一维随机变量x,其一元高斯分布的概率密度函数为:
(1)
式中:μ为均值;σ为标准差。
一元高斯分布由均值和标准差实现唯一确定。
当随机变量数不止一个时,可以推广得到多元高斯分布。对n维随机变量x=(x1,…,xn)T,其期望向量为:
(2)
其协方差矩阵为:
(3)
记K=Var(x),则有:
(4)
式中:Cov(xi,xj)为随机变量xi与xj的协方差。
设μ1、μ2、...、μn为各维度随机变量的均值,则均值向量为:
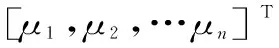
(5)
x的多元高斯分布密度函数为[17]:
(6)
多元高斯分布由均值向量和协方差矩阵实现唯一确定。
2.2.2 高斯过程
在了解高斯过程之前,需要了解一个更为宽泛的概念,即随机过程。如果对于每一个x∈T,f(x)是一个随机变量,则称随机变量族{f(x),x∈T}为随机过程,其中T为参数集,f(x)的所有取值为状态集。如果随机过程{f(x),x∈T}的任意有限维分布都是高斯分布,即对任意x1,x2,…,xn∈T,f(x1)、f(x2)、…、f(xn)都服从n元高斯分布,则称随机过程{f(x),x∈T}为高斯过程[17]。可以将T推广至多维空间,即变量x在多维空间中取值。
高斯过程可以看作是多元高斯分布推广到无限元高斯分布。当对某一现象进行无限维采样时,即为对该现象对应函数进行采样,高斯过程可以看作是函数的分布。高斯过程表示为:
f(x)~N[μ(x),K(x,x′)]
(7)
μ(x)=E[f(x)]
(8)
K(x,x′)=E{[f(x)-μ(x)][f(x′)-μ(x′)]}
(9)
μ(x)为均值函数,返回各个维度的均值。K(x,x′)为协方差函数,也称核函数,返回各个维度之间的协方差矩阵。高斯过程由均值函数和协方差函数实现唯一确定。
核函数是高斯过程的核心,决定高斯过程的性质。核函数的作用是生成协方差矩阵,衡量任意两点之间的关系或距离。最常用的核函数是径向基函数,基本形式为:
(10)
式中:σ1、l为待定超参数。
径向基函数是无限可微的,以此作为核函数的高斯过程具有所有阶数的均方差导数,因此非常光滑。核函数还有Matern内核、有理二次内核、正弦二次方内核等。对于核函数自身的超参数,通常通过最大化边缘似然估计方法来进行选择。
2.2.3 高斯过程回归
贝叶斯定理表达式为:
(11)
D1∶t=[(x1,y1),(x2,y2),…,(xt,yt)]
(12)
yt=f(xt)+εt
(13)
式中:f为未知目标函数;D1∶t为已观测样本;x1、x2、…、xt为决策向量;y1、y2、…、yt为观测值;εt为观测误差;p(D1∶t|f)为在f条件下y的似然分布;p(f)为f的先验概率分布;p(D1∶t)为边际化f的边际似然分布;p(f|D1∶t)为f的后验概率分布。
先验概率分布是对未知目标函数状态的假设,后验概率分布描述通过已观测数据样本对先验概率分布进行修正后未知目标函数的置信度。边际似然分布由于存在概率密度函数的乘积和积分,因此通常难以得到明确的解析式。
贝叶斯定理表明可以通过某一现象的先验分布与似然概率来推测后验分布,高斯过程回归应用了贝叶斯定理。在高斯过程回归中,每一次观测得到新观测数据后都会更新高斯过程的均值函数,使均值函数逐渐逼近真实值。初始均值函数的选取对高斯过程回归结果的影响很小,先验均值函数可以取0。
对于无噪声高斯过程回归,对于已有数据(x,f),将高斯过程的先验分布表示为f(x)~N(0,Kff),现有一些新的观察数据(x*,y*),假设y*与f服从联合高斯分布,于是有:
(14)
Kff=K(x,x)
(15)
Kfy=K(x,x*)
(16)
Kyy=K(x*,x*)
(17)
后验分布为[18]:
(18)
式(18)表明给定数据(x*,y*)后的函数分布仍然是一个高斯过程。
(19)
联合高斯分布变为[18]:
(20)
高斯过程回归的流程为根据已有的观测数据假设一个高斯先验分布,观测到一些新的数据,基于先验和联合高斯分布假设计算得到高斯后验分布的均值与协方差。
随机过程在连续域中的每个点都是随机变量,也就是说每一个观测点都是巧合出现在观测位置。每个点都以一定概率出现在状态空间的任意位置上,因此任意一组数据都可以看作是某一个随机过程的样本函数。高斯过程回归就是将观测数据集合看作高斯过程的样本函数。
在铣削工艺参数优化的研究中,将优化目标与影响因素之间看作是随机的函数关系,即满足高斯过程。已有观测数据和新观测数据均来源于同一个高斯过程,因此上述先验高斯分布假设和联合高斯分布假设均可满足,高斯过程回归可以很好地应用于铣削工艺参数优化场景。
2.3 采集函数
贝叶斯算法依靠主动选择策略将历史信息和不确定性相结合,可以有效平衡宽度搜索和深度搜索之间的关系,进而减少非必需的优化目标评估,同时通过将采集函数最值化,推荐优化参数组合。
由此可见,采集函数的作用有两个。第一,确定下一次用于评估的评估点。第二,平衡宽度搜索与深度搜索的关系,使贝叶斯算法可以避开局部最优,并减少对优化目标的评估次数。
常用的采集函数其策略有基于增益的策略和置信边界策略。
2.3.1 增益概率
优化目标考虑望大优化,增益概率的原理为找到未知评估点的评估值比已知最优评估值更优的概率,选取这些点中概率最大的点,对于相对最优评估值的具体增益值不作考虑。增益概率数学模型PI(x)为:
PI(x)=P[F(x)≥F(x+)+ξ]
=Φ{[μ(x)-F(x+)-ξ]/σ(x)}
(21)
式中:F(x)为x的优化目标函数值;F(x+)为到目前为止最优的目标函数值;ξ为平衡参数;Φ为标准正态分布概率密度函数;σ(x)为协方差函数。
平衡参数用于平衡宽度搜索和深度搜索的关系,一般由人为设定。
2.3.2 增益期望
增益概率能够选择概率最大的评估点,将所有增益看作是等量的,不反映增益量。增益期望考虑具体增益的多少。增益期望数学模型EI(x)为:
EI(x)=
(22)
Z=[μ(x)-F(x+)-ξ]/σ(x)
(23)
2.3.3 置信上界和置信下界
置信边界策略具有明显的概率意义,通过正态分布置信区间的概念反映宽度搜索的不确定度。置信上界UCB应用于望大优化,置信下界LCB应用于望小优化,数学模型UCB(x)、LCB(x)分别为:
UCB(x)=μ(x)+kσ(x)
(24)
LCB(x)=μ(x)-kσ(x)
(25)
式中:k为平衡参数。
平衡参数用于平衡宽度搜索和深度搜索的关系,一般由人为设定。
3 试验
3.1 优化模型
金属铣削加工中,起主要影响的工艺参数是主轴转速、进给速度、铣削深度、铣削宽度。将这四个工艺参数设为优化变量。
不同加工场景对应不同的加工目标,如加工时间、加工能耗、加工质量等。在金属铣削加工领域中,加工目标可以分为约束类加工目标和极值类加工目标[19]。对于约束类加工目标,只需将目标控制在某个范围内。对于极值类加工目标,需要使目标达到极值。将加工质量作为极值类加工目标,具体细化为极小化尺寸偏差与形位偏差。由此,选择孔径偏差、台阶宽度偏差、台阶两侧平行度、台阶高度偏差、孔深度偏差作为优化目标指标。
优化参数的调整受到多方面约束条件限制,约束条件可以分为外在约束条件和内在约束条件。外在约束条件指外部订单或人员的约束,内在约束条件指机床、刀具等设备自身的限制,以及加工工艺设计的约束。本研究只考虑内在约束条件。
受机床性能、刀具寿命、铣削力等限制,主轴转速与进给速度只能在一定范围内调整。受机床控制精度的限制,主轴转速与进给速度的取值精度也有一定限制。受刀具性能、刀具寿命、工件材料、铣削力等多方面影响,铣削深度与铣削宽度同样受到限制,并且受机床控制精度的限制,铣削深度与铣削宽度的取值精度也有一定限制。
3.2 试验条件
以铣削加工为试验场景,研究以铣削工艺参数为优化变量的加工质量优化方法。
试验的加工条件为湿式加工,加工设备为五轴加工中心,加工刀具为整体钨钢三刃立铣刀,测量设备为三坐标测量机,样件材料为6061铝合金,试验样件特征有平面、台阶、孔,毛坯尺寸为30 mm×30 mm×50 mm,如图1所示。
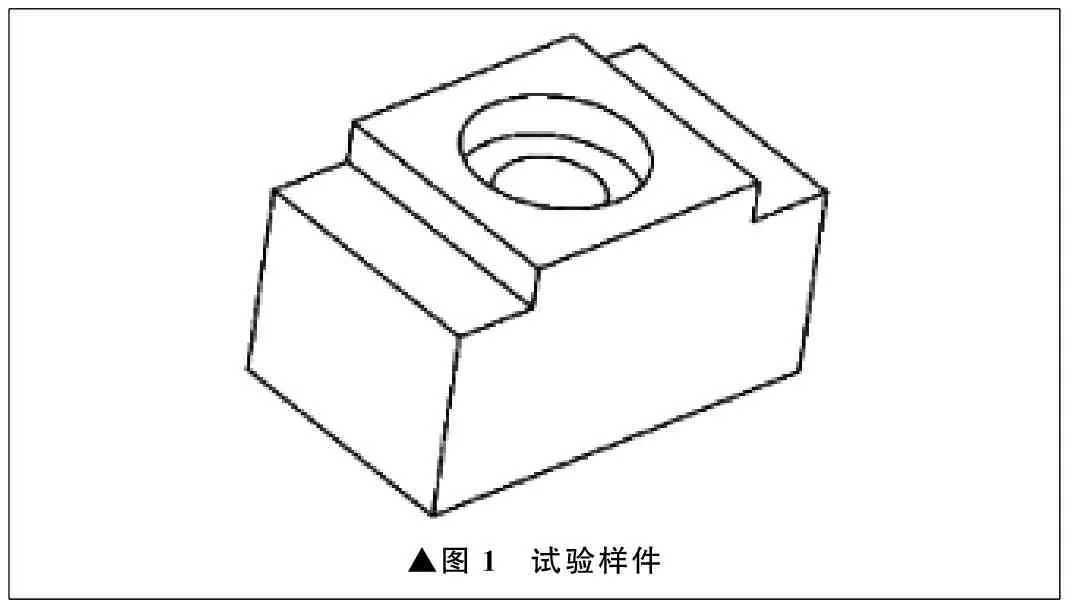
▲图1 试验样件
3.3 田口法试验设计
田口法强调产品质量的提高不是通过检验,而是通过设计。相比于依靠工程师经验和传统试验方法,田口法是一种高效率、低成本的质量工程方法。
(1) 确定试验目的和要求。通过田口法试验确定工艺参数与加工质量的关系,优化工艺参数。
(2) 确定待改善的优化目标。以尺寸偏差与形位偏差作为优化目标,细化为具体的优化指标,并以归一化指标作为总优化目标。
(3) 确定影响优化目标的因子。将以上述四个优化变量作为影响优化目标的因子。
(4) 确定合适的各因子水平。综合考虑约束条件和试验次数、成本的限制,试验中每个因子取四个水平,见表1。
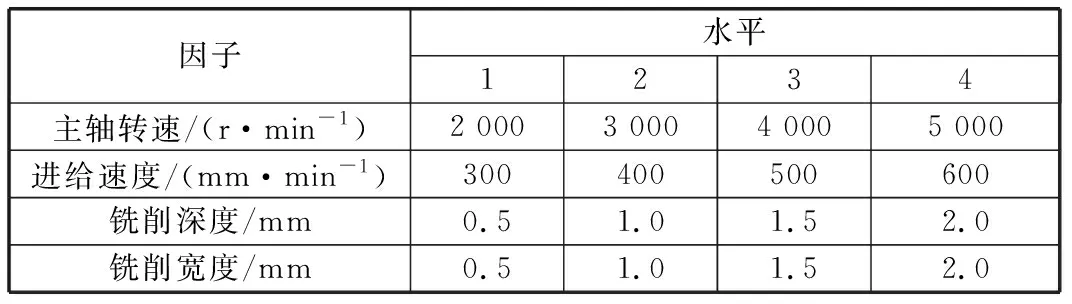
表1 铣削加工试验因素水平
(5) 设计田口表。通过Minitab软件,选取五因子四水平田口表L16(45)的前四列安排试验,见表2。
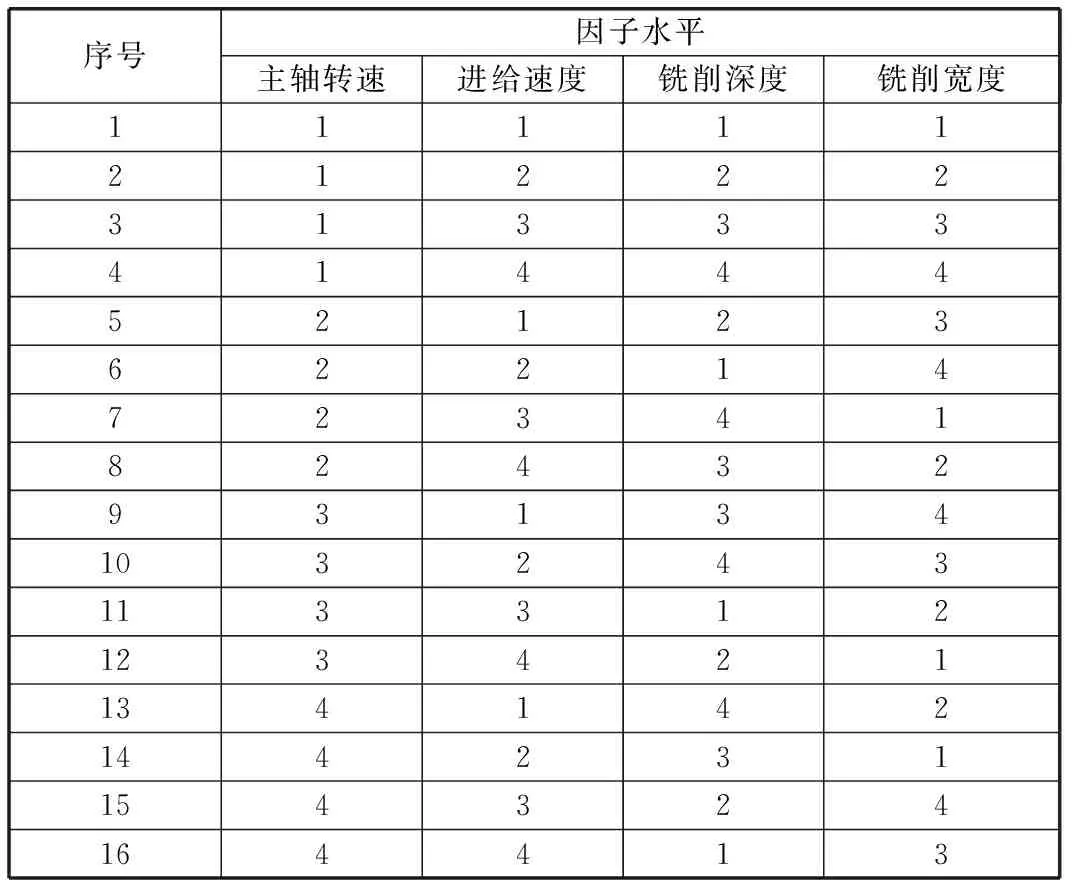
表2 田口表
(6) 依据田口表实施试验。按照不同的因子组合组织加工、测量试验。
(7) 数据记录与分析。记录细化指标值,计算归一化指标值,通过Minitab软件进行极差分析,得出优化结果。
将田口法作为贝叶斯算法的对比试验。
3.4 贝叶斯算法试验设计
贝叶斯算法优化目标和优化变量与田口法相同。优化空间时,田口法各因子选取的水平为离散值,采样间隔相对较大,容易出现优值落在两采样值之间的情况,优化效果相对较差。若要缩小采样间隔,则会增加水平数,总体试验次数与调优成本呈指数上升,也会增加冗余试验次数。贝叶斯算法在理论上不限制采样间隔大小,可以设置更密的采样点。另一方面,由于更快的收敛速度及更佳的全局搜索性能,贝叶斯算法可以保证在更大搜索范围内的调优效果和收敛速度,能够避免不必要的寻优试验,有效降低工艺参数配置寻优试验的成本。考虑约束条件限制后,设定贝叶斯算法优化空间,见表3。

表3 贝叶斯算法优化空间
在其它调优场景中,可以根据实际情况增加优化空间样本点,以提高调优成本为代价提高调优精度。
试验采用适用于连续参数搜索的高斯过程回归作为概率代理模型,选择Matern内核作为核函数,采用置信下界策略作为采集函数,并且将平衡参数设置为1.96。
贝叶斯算法流程如图2所示。鉴于贝叶斯算法冷启动的特点,需要进行初始化,即随机产生初始参数组合参与试验,并按表3设置优化空间。初始化完成后,通过加工、测量获得归一化目标函数值。之后通过终止条件判断是否继续优化,若继续优化,则更新参数与归一化目标函数值的数据集合,并根据新加入的观测数据更新高斯分布。最后通过最小化置信下界获取下一轮优化的推荐参数组合,为下一次试验做好准备。若触发终止条件,则输出优化结果。
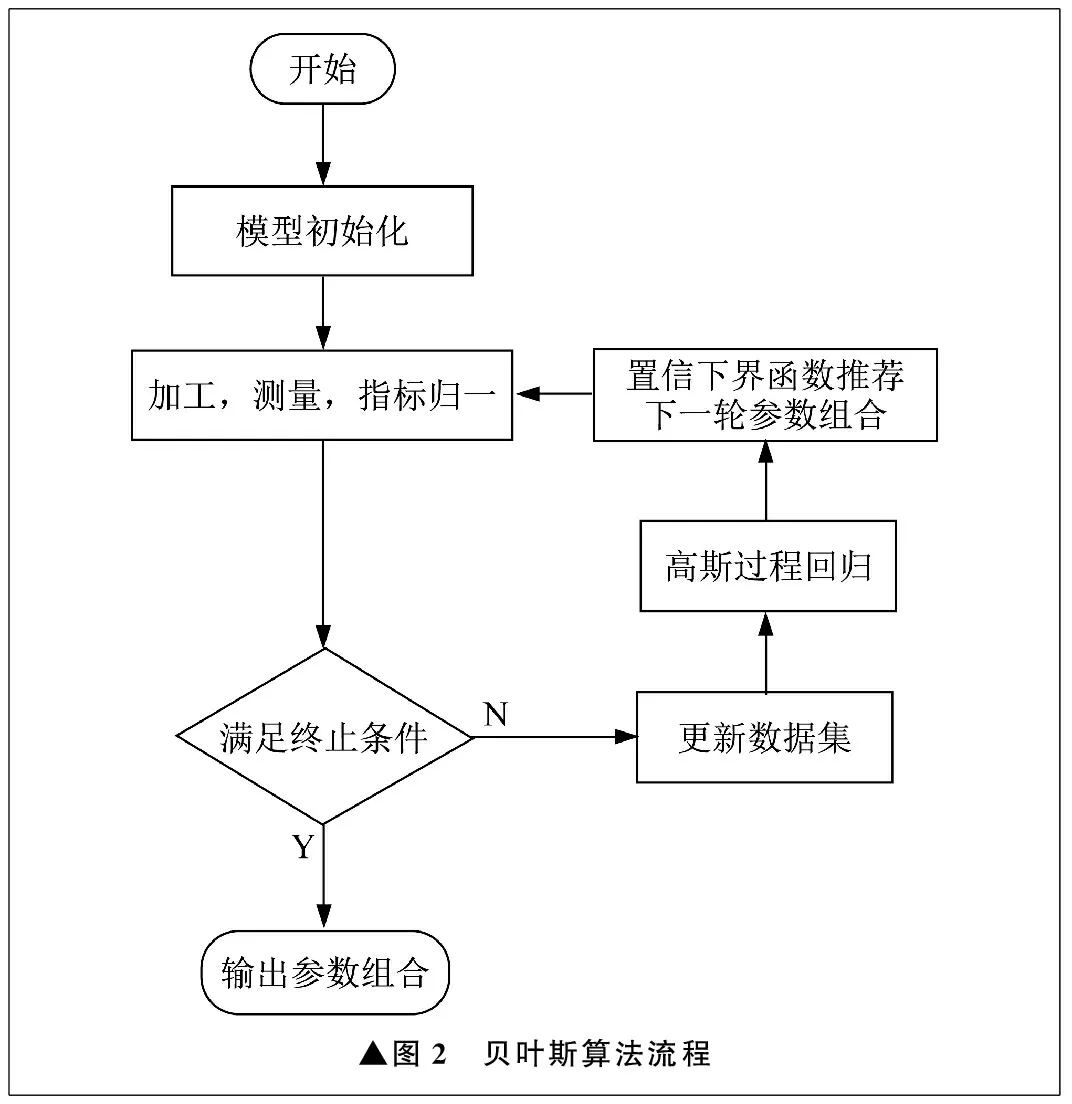
▲图2 贝叶斯算法流程
3.5 归一化
试验涉及的细化指标量纲一致,且均为负向指标,因此不需要数据同向化与标准化处理,仅需要进行加权归一。多目标综合加权方法有层次分析法、灰色关联分析法、主成分分析法等。利用层次分析法将关于多个尺寸公差和形位公差目标的多目标优化转化为各目标加权归一,得到总目标的单目标优化。
层次分析法通过构造子目标的重要性判断矩阵,用数学方法表示决策者的想法,可以处理难以定量分析的复杂问题。另一方面,引用层次分析理论可以在优化过程中加入主观意愿,使优化得到的工艺参数更符合实际生产的要求。
(1) 建立层次分析模型,如图3所示。
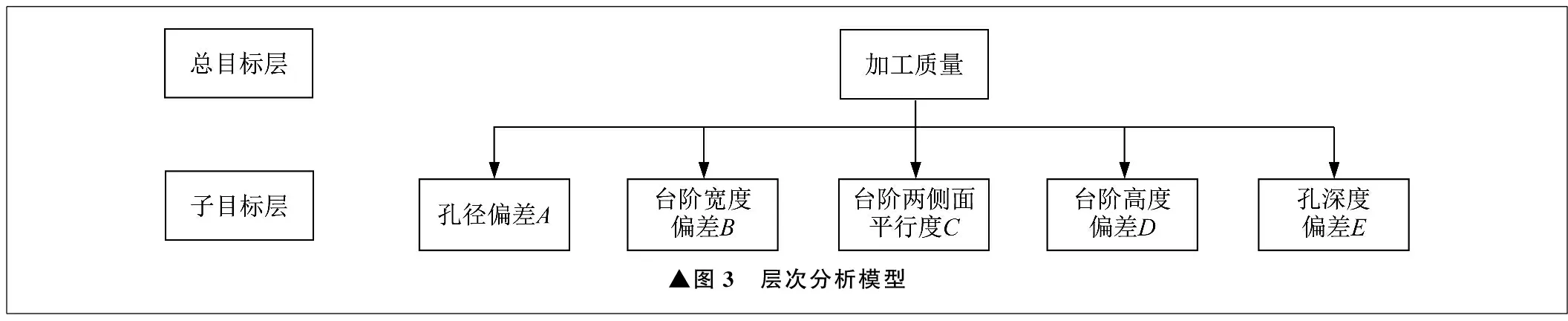
▲图3 层次分析模型
(2) 构造重要性判断矩阵。通过专家打分和经验构造重要性判断矩阵,各子目标对总目标的相对重要性比较见表4。
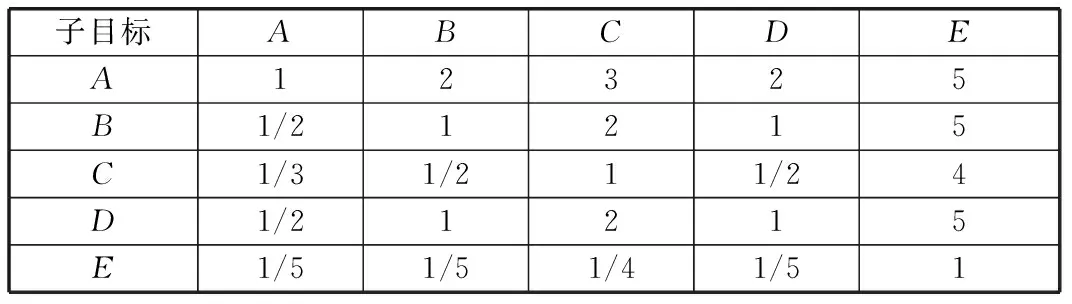
表4 各子目标相对重要性
(3) 计算判断矩阵最大特征值及对应的特征向量。最大特征值λmax为5.095 1,所对应的特征向量为[-0.734 0 -0.438 8 -0.259 2 -0.438 8 -0.094 5]T。
(4) 一致性检验。层次分析法通过一致性指标检验各子目标相对重要性设置的合理性。一致性指标CI为:
(26)
一致性比率CR为:
CR=CI/RI
(27)
式中:RI为判断矩阵的随机一致性指标,对于5阶判断矩阵,取1.12。
通过计算得到一致性指标为0.023 8,一致性比率为0.021 25。一致性比率小于0.1,认为判断矩阵与专家经验一致,通过一致性检验。
(5) 确定各子指标权重。将特征向量归一化,即可得到权向量为[0.373 4 0.223 3 0.131 9 0.223 3 0.047 1]T。
(6) 归一化指标。得到归一化指标为:
F=0.373 4A+0.223 3B+0.131 9C
+0.223 3D+0.048 1E
(28)
加工质量归一化指标值越小,表示加工质量越高。
3.6 结果分析
通过对田口法优化结果与贝叶斯算法优化结果进行对比,验证贝叶斯算法的优越性。田口法极差分析结果见表5。由极差分析结果可知各因子对归一化指标的影响程度从大到小依次为主轴转速、铣削宽度、铣削深度、进给速度。对田口法得到的优化参数组合进行补充验证,并作为贝叶斯算法结果的对比组。
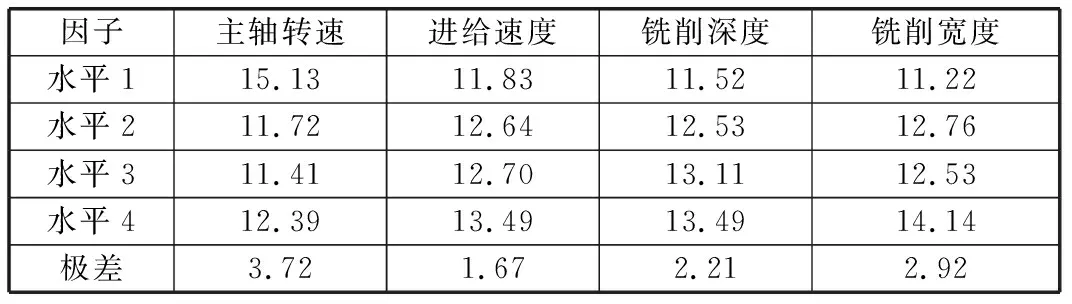
表5 田口法极差分析结果
贝叶斯算法试验为交互式试验,按照贝叶斯算法的推荐参数组织每一轮试验,上一轮试验的输出是下一轮试验的输入,试验顺序严格且各轮推荐相互关联。贝叶斯算法试验结果见表6。其中,前两组试验结果为初始化试验中的两组初始值,并以此为先验知识,经贝叶斯算法处理,得出迭代次数为1的试验因素组合。
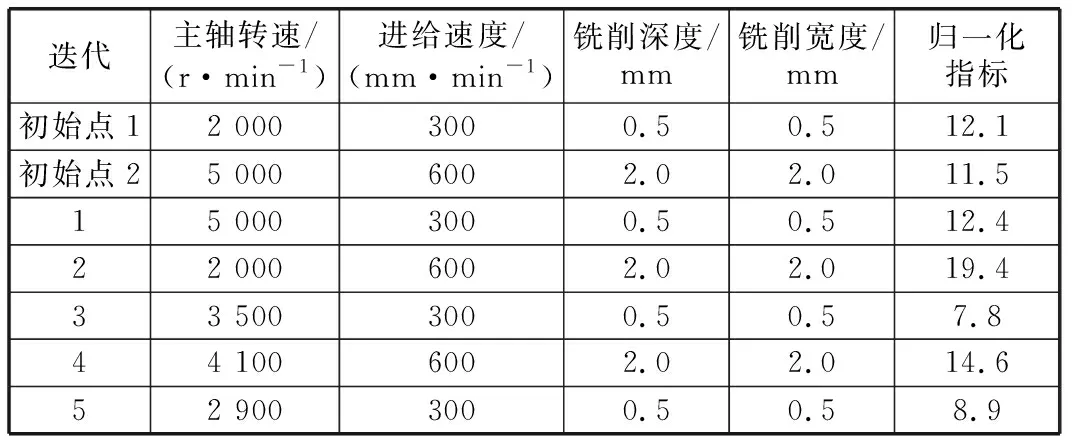
表6 贝叶斯算法试验结果
贝叶斯算法试验结果与田口法优化结果对比见表7。从试验结果看,贝叶斯算法优化成本降低58.8%,优化效果提高9.3%,在提升优化效果的同时极大节省了试验成本,验证贝叶斯算法在铣削工艺参数配置优化中的有效性。贝叶斯算法具有对复杂和高试验成本场景的普适性,可以将贝叶斯算法推广应用至其它金属铣削加工的优化场景中。

表7 贝叶斯算法与田口法效果对比
4 结束语
笔者分析了贝叶斯算法概率代理模型与采集函数的基本原理,研究了贝叶斯算法在金属铣削加工工艺参数配置优化中的可行性,提出了基于贝叶斯算法的铣削工艺参数配置优化方法。
以尺寸偏差与形位偏差最小为优化目标,以铣削工艺参数为优化变量,建立铣削加工工艺参数优化模型,基于层次分析理论研究子指标的综合加权方法,设计田口法与贝叶斯算法,完成铣削工艺参数优化试验。通过对比,表明贝叶斯算法在优化速度与优化效果两个维度的表现均优于田口法。应用贝叶斯算法对工艺参数进行优化,可以在大幅降低优化成本的同时提高加工质量。在实际生产中,可以在金属铣削加工工艺参数配置优化场景中推广应用贝叶斯算法。考虑能量消耗、加工效率、零件表面质量的工艺参数多目标优化是后续研究重点。

