坐卧式下肢康复机器人的机构设计与仿真*
□ 黎颢宇 □ 冯永飞,2 □ 刘国伟 □ 彭 旭 □ 牛建业 □ 尹东颖
1.宁波大学 机械工程与力学学院 浙江宁波 315211 2.唐山海佑机器人科技有限公司 河北唐山 063200 3.燕山大学 机械工程学院 河北秦皇岛 066004
1 设计背景
脑卒中是一种常见疾病[1],在人口老龄化背景下,我国目前约有700万脑卒中患者[2]。研究表明,脑卒中患者经过康复治疗后,下肢功能会明显得到改善[3]。然而,传统康复训练需要治疗师帮助患者进行一对一治疗,治疗周期长、成本高[4-5]。下肢康复机器人的出现不仅有效解决了以上问题,而且为脑卒中患者下肢运动功能的恢复提供了新思路[6]。
康复机器人技术在患者康复过程中具有重要意义,近年来,下肢康复机器人成为机器人领域的研究热点[7]。根据患者的训练姿态,可以将下肢康复机器人分为站立式和坐卧式两类。站立式下肢康复机器人以美国Vanderbilt大学设计的下肢康复机器人为代表[8],使用者可以借助前臂支撑拐杖或自动助步器等设备来维持身体平衡,安装在臂部组件内的充电电池为机器人提供动力[9]。瑞士苏黎世联邦理工学院研发的康复机器人同样是站立式下肢康复机器人[10],将悬挂系统与跑步机结合起来,患者的腿部关节可以通过预先设定的步态运动模式来引导,进而达到康复效果。类似的站立式下肢康复机器人还有日本筑波大学研制的下肢外骨骼式康复机器人[11]。站立式下肢康复机器人通过对人体下肢进行一定形式的固定,带动下肢进行步态训练,一般设置有减重设备,以减轻患者下肢对人体自身重力的承受。
相比站立式下肢康复机器人,坐卧式下肢康复机器人更适合脑卒中早期卧床患者。Yan Hao等[12]提出的坐卧式下肢康复机器人采用模块化设计,能够进行下肢髋、膝、踝三个关节的独立训练,根据预设信息,可以对不同患者自动进行腿长匹配。美国研究人员开发的一款坐卧式下肢康复机器人可以使患者的四肢按照特定的轨迹同时进行运动,但运动轨迹不可调整,并且功能较为单一[13]。这一款坐卧式下肢康复机器人成本较低,可以为患者减轻经济压力。坐卧式下肢康复机器人还包括土耳其Yildiz科技大学和Marmara大学联合研制的下肢康复机器人[14]。当然,现有的大部分坐卧式下肢康复机器人仅能够满足患者在矢状面内的康复需求。
为了恢复患者下肢精细化的运动能力,康复机器人需要对患者进行真实场景下的复杂作业训练。由于空间多自由度康复机械腿的结构较为复杂,因此理论支撑不足,康复机器人在临床康复方面还未得到广泛应用。针对脑卒中早期卧床患者,研究具有冠状面与矢状面运动功能的下肢康复机器人具有重要意义。笔者设计了一种新型坐卧式下肢康复机器人,结合旋转副滑动副平面二自由度机构,通过牵引患者足部,来实现患者下肢髋关节的屈伸与外展内收、膝关节的屈伸、踝关节的跖屈与背屈。
2 结构
所设计的坐卧式下肢康复机器人的结构如图1所示,主要由底架、座椅升降组件、下肢康复训练组件组成。下肢康复训练组件作为主要的执行机构,分为左、右对称的两部分,对应患者的左右腿。
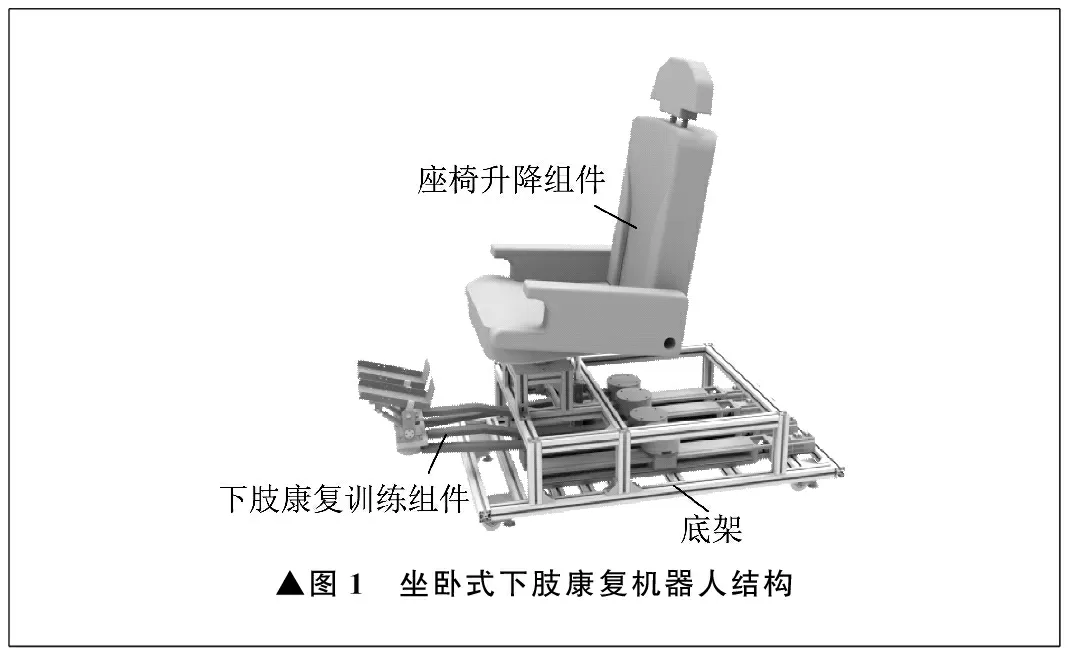
▲图1 坐卧式下肢康复机器人结构
3 下肢康复训练组件
下肢康复训练组件如图2所示。下肢康复训练组件的本质是平面二自由度机构。伺服电机通过对应的线性模组驱动滑块,实现运动。滑块通过滑块部旋转副与方管进行连接,滑块部旋转副的轴线与水平面垂直。方管的另一端与脚部旋转副相连,在脚部旋转副上方固定有踏板组件。当两个伺服电机以相同转速工作时,线性模组上的滑块带动两个滑块部旋转副同步向前或向后,进而实现患者矢状面髋、膝、踝关节的屈曲与伸展运动。当两个伺服电机的转速存在速度差时,踏板组件会带动患者实现髋关节在冠状面内的外展与内收。
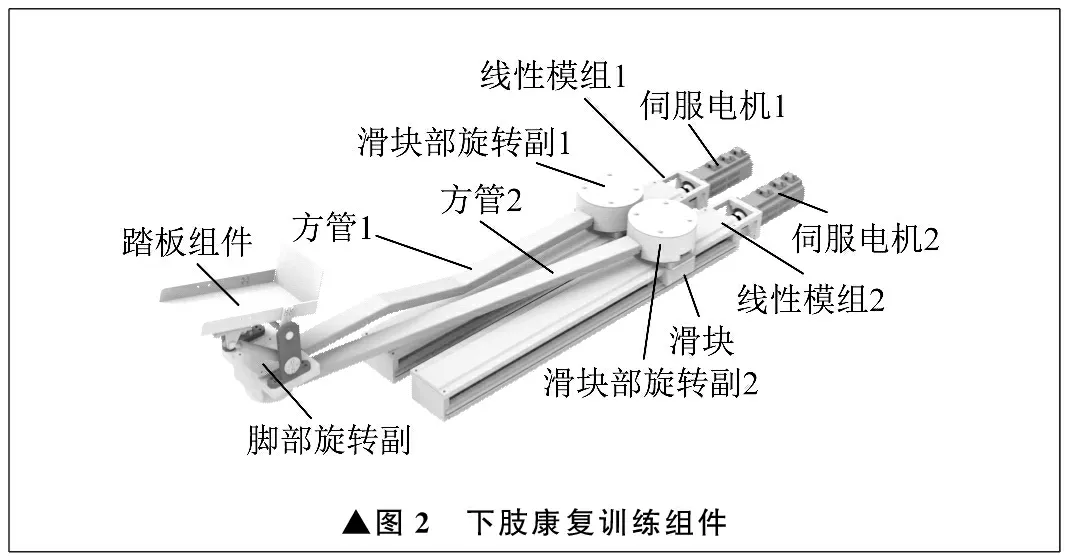
▲图2 下肢康复训练组件
为了保证下肢康复机器人在冠状面内的安全性,在滑块部旋转副处设有机械限位,如图3所示。滑块部旋转副开有导槽,与滑块固定为一体的支撑托板上设有限位螺栓,可以对滑块部旋转副的转动范围进行限制。
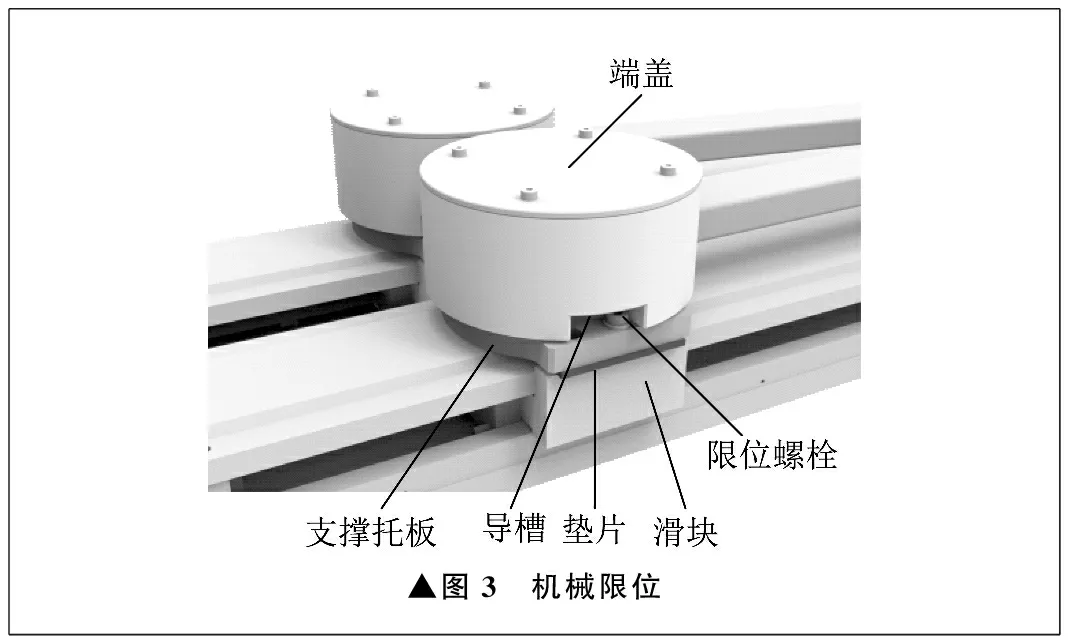
▲图3 机械限位
踏板组件如图4所示。踏板通过固定支座与脚部旋转副连接,通过连接板与固定支座相连。当踏板上受到患者脚部施加的力时,气弹簧可以伸缩,使踏板绕转轴5转动。当踏板带动患者脚部进行运动时,患者对踏板施加的力将产生变化,通过下肢的姿态变化自动调节矢状面内的角度。
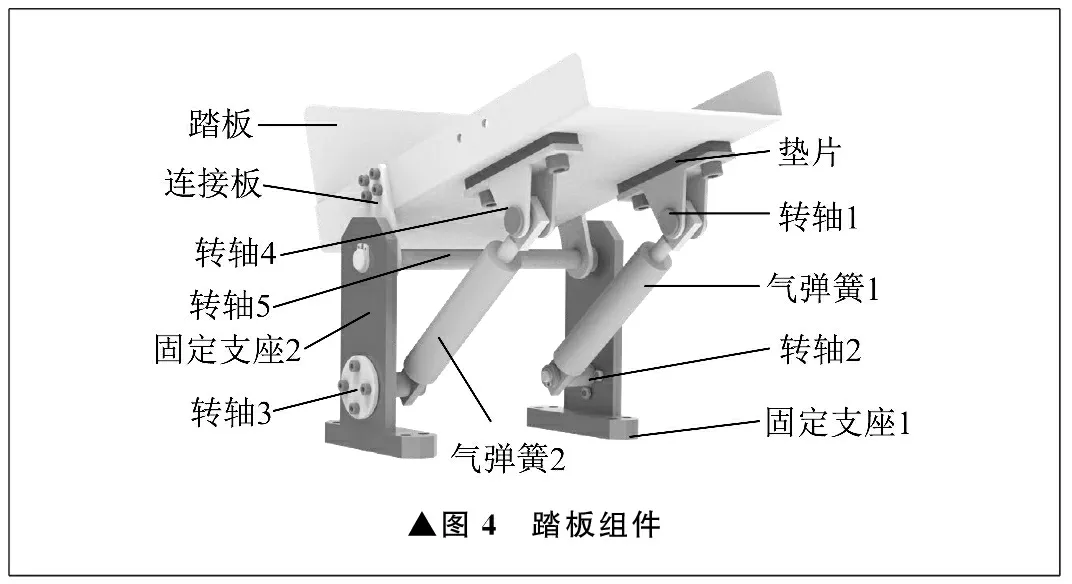
▲图4 踏板组件
4 座椅升降组件
座椅升降组件如图5所示。电动推杆的固定端固定于底架上,移动端固定于连接板1。连接板1与座椅固定连接。两个直线轴承固定于连接板2,直线轴承的上端固定于连接板1,连接板2与底架连接。座椅的固定由直线轴承与电动推杆共同完成。在座椅升降过程中,通过电动推杆的推力带动直线轴承在平行于电动推杆升降的方向移动,实现座椅高度的调节。
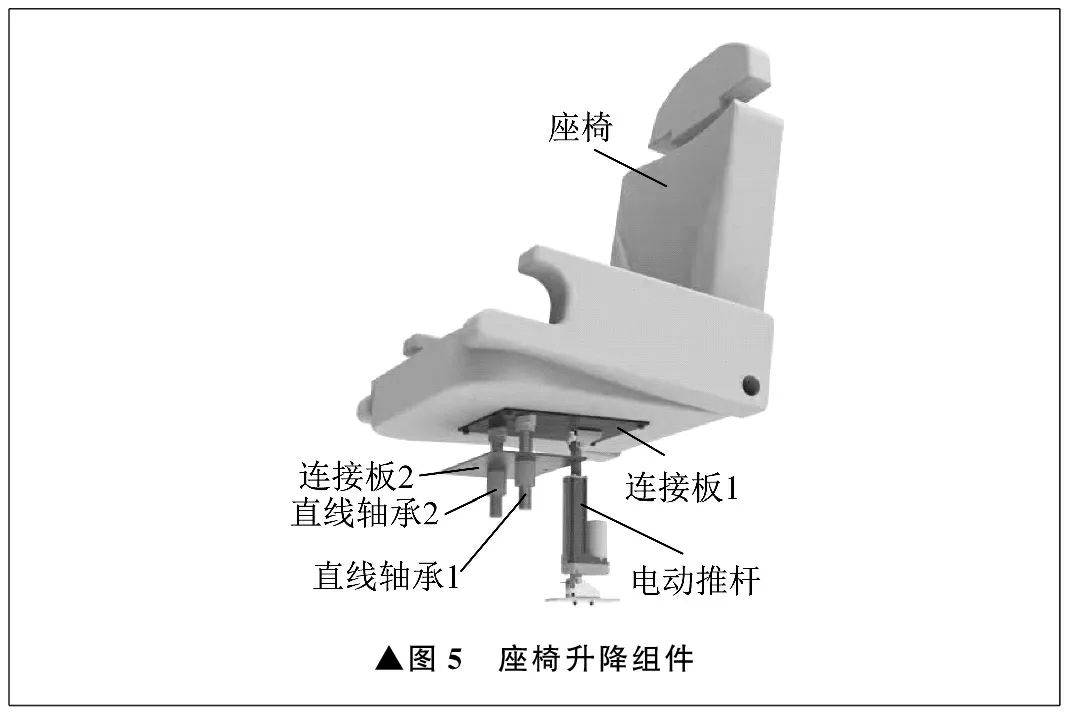
▲图5 座椅升降组件
5 速度雅可比矩阵求解
选取左侧下肢康复训练组件作为研究对象,建立连杆模型,如图6所示。连杆AB、AD分别表示方管1和方管2,S1、S2分别表示线性模组上的滑块。连杆AB与滑块S1、连杆AD与滑块S2均通过转动副连接。以滑块S1所在的线性模组轴心建立Y轴,以垂直于Y轴方向建立X轴,以座椅中心在Y轴方向的投影为坐标原点O。设连杆末端点A坐标为(xa,ya),连杆AB、AD的长度分别为l1、l2。连杆AB与Y轴的夹角为θ1,连杆AD与直线ED的夹角为θ2。C1、C2分别代表连杆AB、AD的质心,设C1的坐标为(xC1,yC1),C2的坐标为(xC2,yC2),BC1的长度为R1,DC2的长度为R2。滑块S1、S2所在轴线之间的距离为m,滑块S1、S2到X轴的距离分别为y1、y2。
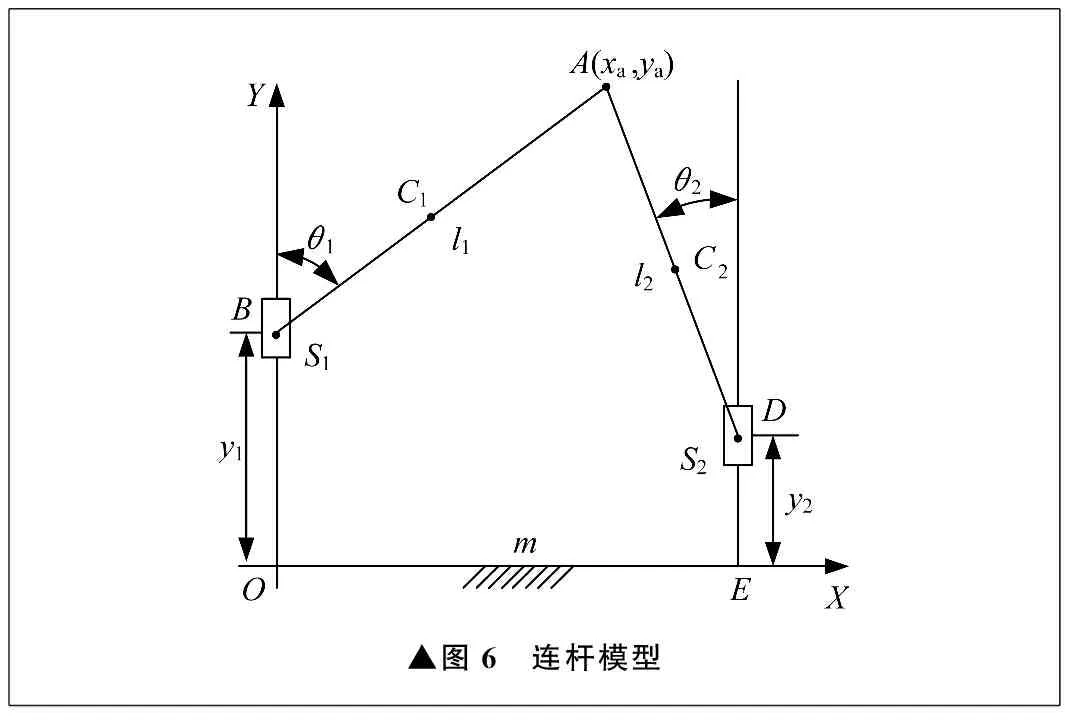
▲图6 连杆模型
根据杆间约束,可以列出方程:
(1)
对于坐卧式下肢康复机器人,有约束:
(2)
由式(1)、式(2)可以求得点A位置的正解为:
(3)
(4)
(5)
(6)
(7)
(8)
点A位置逆解公式为:
(9)
对式(9)等号两侧求导,可得:
(10)
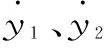
将式(10)进一步转换,可得矩阵形式:
(11)
由式(11)可得速度雅可比矩阵J为:
(12)
6 基于轮廓误差的交叉耦合控制
传统的控制方法忽略操作空间中的误差,难以保证机器人在操作空间中的轨迹跟踪精度。笔者提出基于轮廓误差的交叉耦合控制,以达到对末端误差直接进行干预的目的,进而提高坐卧式下肢康复机器人的安全性。
6.1 轨迹规划
为保证坐卧式下肢康复机器人的训练轨迹不对电气设备产生冲击,需要验证所设计的训练轨迹关于时间的位移s、速度v、加速度a等函数曲线是否平滑且柔顺。
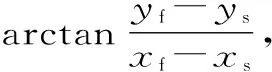
l(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5
(13)
式中:ai为待求解因数;t为时间。
l(0)=0
(14)
l(tf)=l
(15)

(16)
(17)
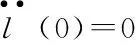
(18)
(19)
结合式(13)~式(19),对因数ai进行求解,可得点A位移s、速度v、加速度a关于时间t的函数多项式,并沿X轴和Y轴分解,得:
(20)
(21)
(22)
(23)
(24)
(25)
6.2 轮廓误差模型
轮廓误差定义为当前实际位置到期望轨迹的最短距离。前文设计的训练轨迹为直线,由此对直线轮廓的误差进行建模分析。直线轮廓误差模型如图7所示,设训练轨迹为平面坐标系中的直线OT。直线OT与X轴正方向夹角为θ,点T为点A的目标位置,其坐标为(xT,yT),点P为点A的实际位置,其坐标为(xP,yP)。
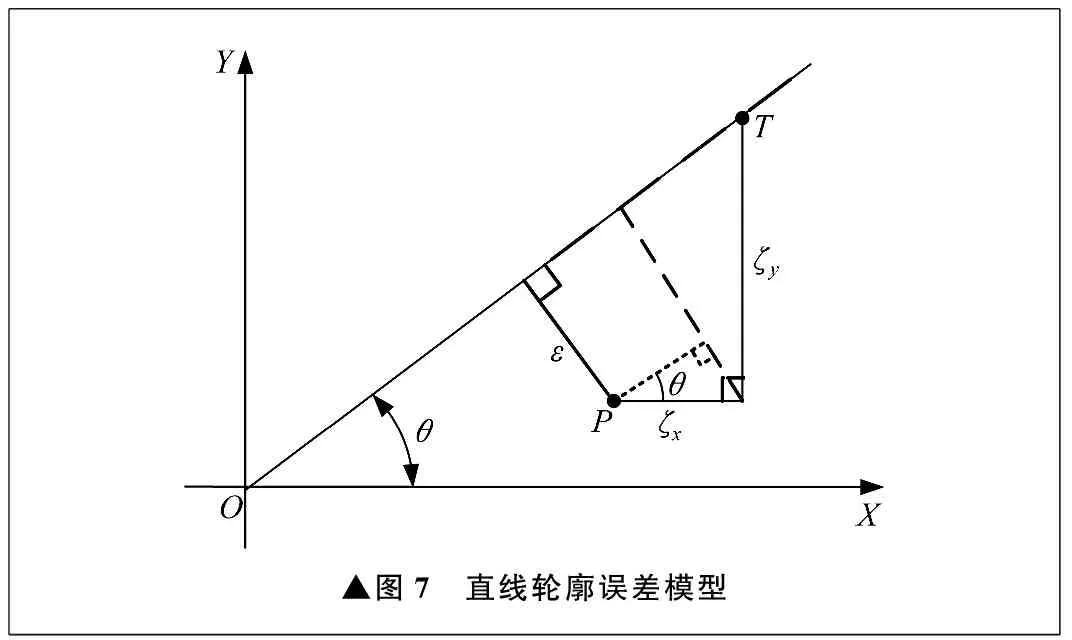
▲图7 直线轮廓误差模型
根据直线轮廓误差模型的几何关系,可得X轴方向的轮廓误差ζx为xT-xP,Y轴方向的轮廓误差ζy为yT-yP。由平面轮廓误差的定义可知,点A的轮廓误差ε为:
ε=ζycosθ-ζxsinθ
(26)
6.3 比例微分交叉耦合控制器
传统比例微分控制结构如图8所示。传统的多轴控制各关节多采用传统比例微分控制,各轴之间独立进行控制,控制过程中没有考虑轮廓误差的大小。交叉耦合控制根据轮廓误差,结合控制系统的具体结构,按照特定方式将轮廓误差补偿到各轴。
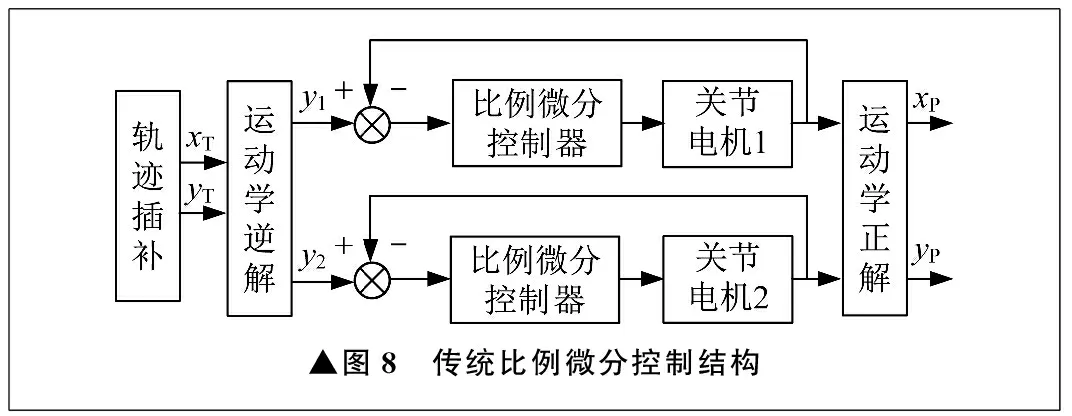
▲图8 传统比例微分控制结构
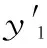
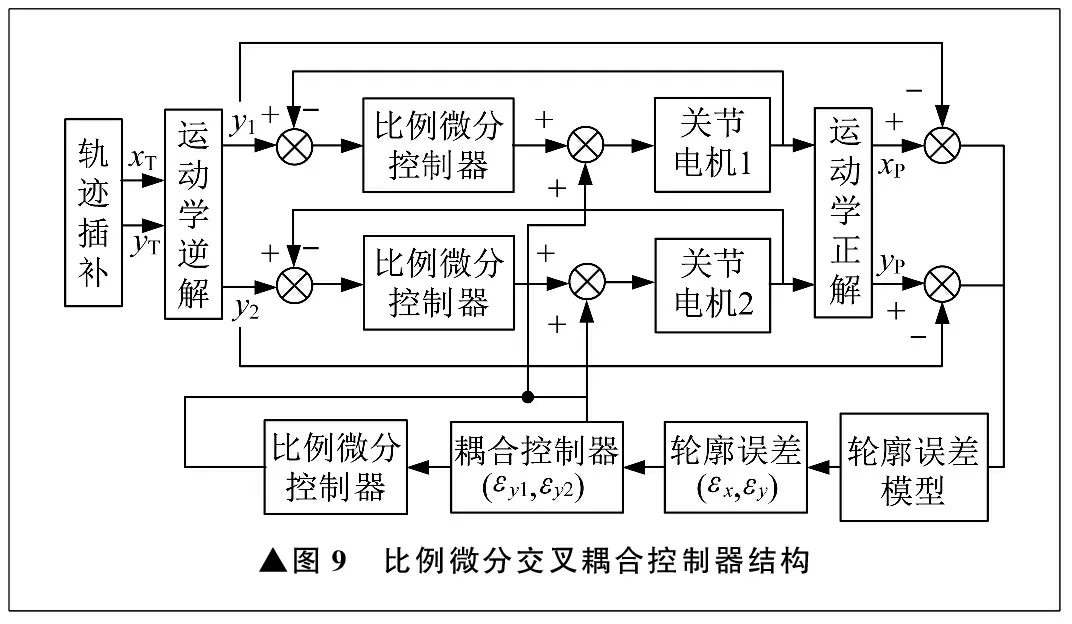
▲图9 比例微分交叉耦合控制器结构
(27)
滑块S1、S2的轮廓误差εy1、εy2通过比例微分控制器进行处理,将处理后的结果作为各轴比例微分控制器输入的一部分。
6.4 仿真
规定训练轨迹起始坐标为(-10 cm,45 cm),终点坐标为(5 cm,90 cm),可以得到训练轨迹的位移、速度、加速度多项式为:
l(t)=0.474 3t3-0.071 2t4+0.002 8t5
(28)
(29)
(30)
为了更直观地判断训练轨迹是否平滑且柔顺,通过MATLAB软件绘制笛卡尔空间位移、速度、加速度曲线,依次如图10、图11、图12所示。由图10~图12可以看出,X轴、Y轴方向上的位移、速度、加速度均满足平滑且柔顺的要求。
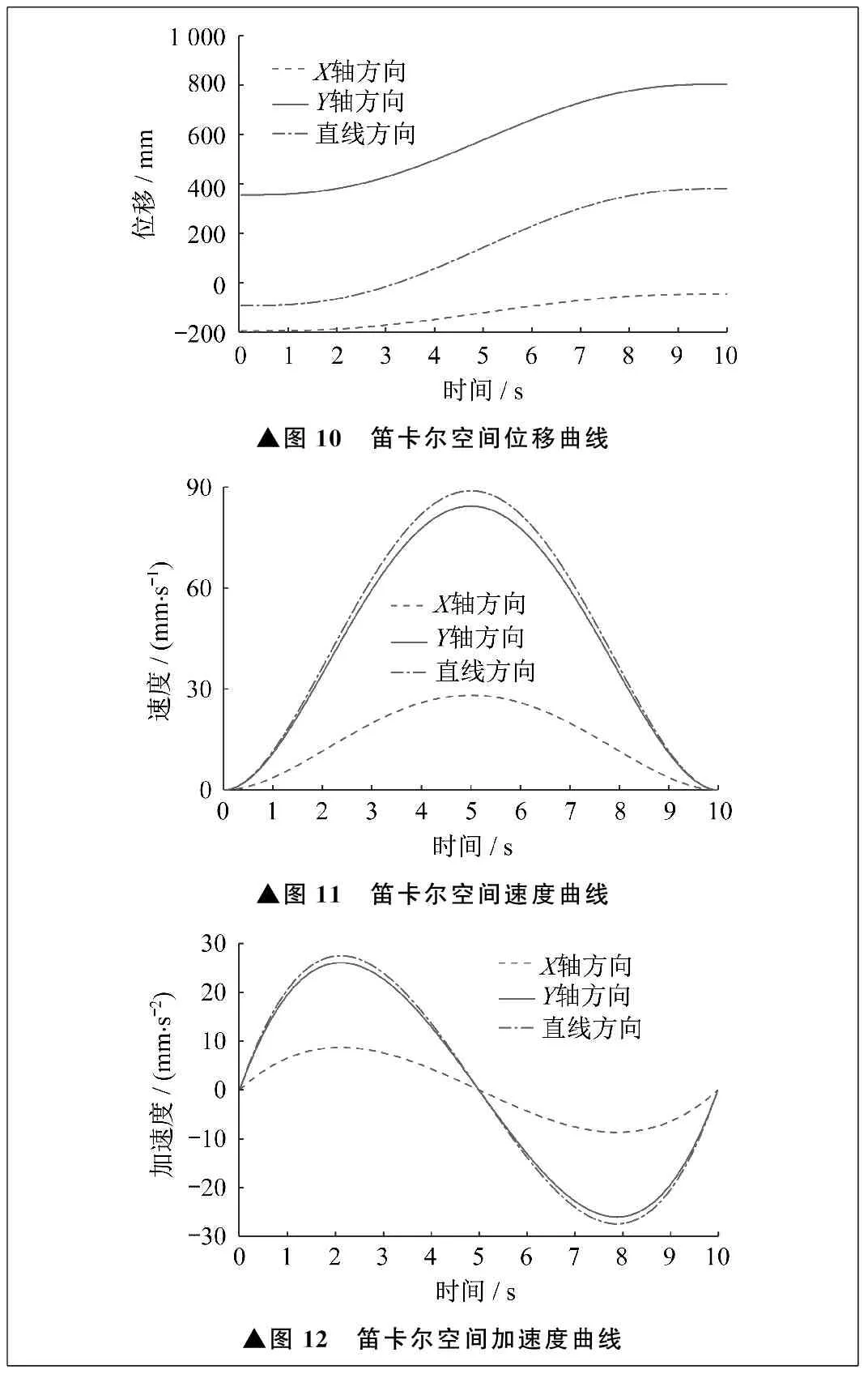
▲图10 笛卡尔空间位移曲线▲图11 笛卡尔空间速度曲线▲图12 笛卡尔空间加速度曲线
滑块S1、S2的位移、速度、加速度曲线依次如图13、图14、图15所示。由图13~15可以看出,经过规划的直线轨迹在滑块S1、S2处的位移、速度、加速度均平滑连续。
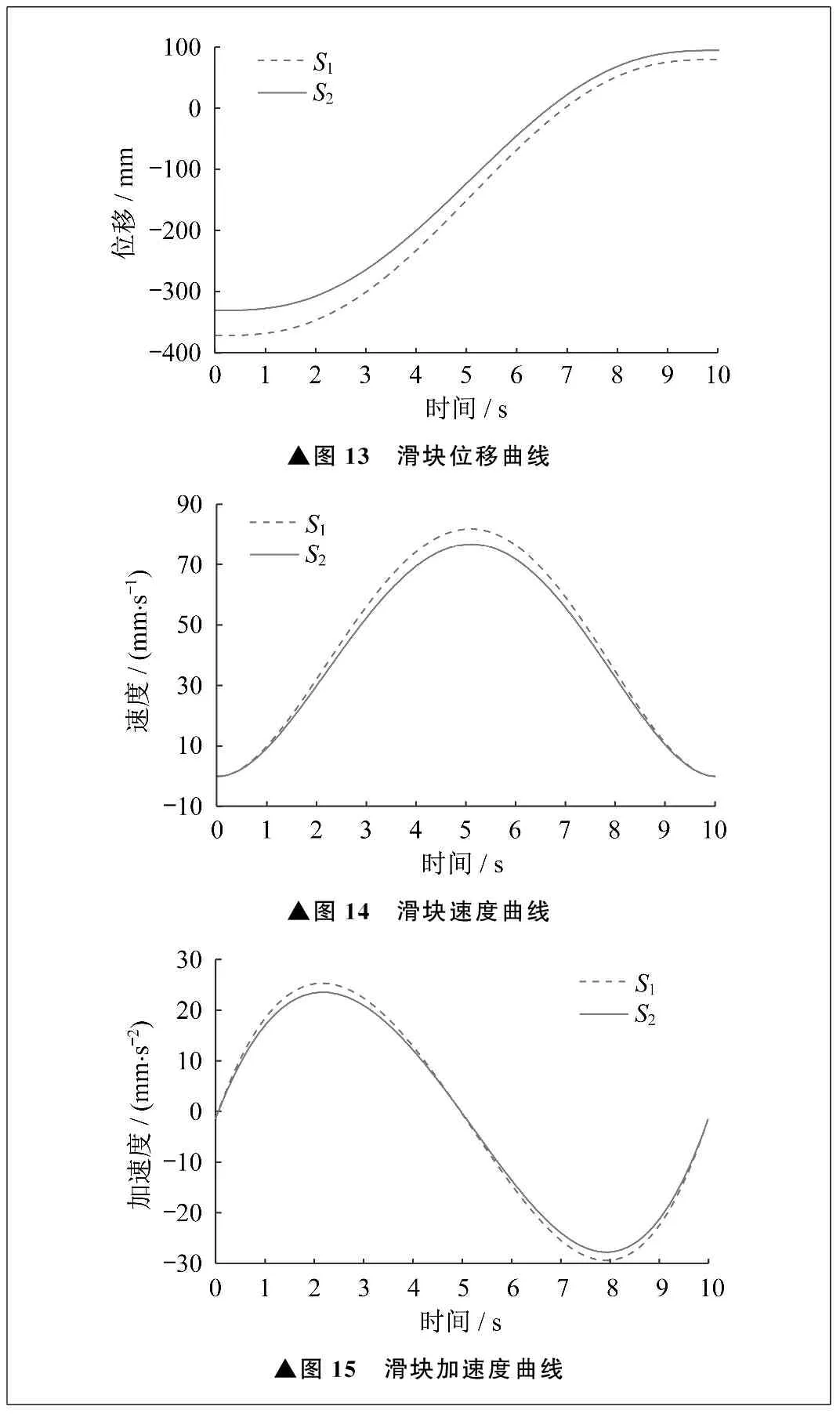
▲图13 滑块位移曲线▲图14 滑块速度曲线▲图15 滑块加速度曲线
为了验证比例微分交叉耦合控制器的正确性,进一步以该直线轨迹作为参考轨迹,分别以传统比例微分控制和比例微分交叉耦合控制作为控制策略,以前文建立的连杆模型作为控制对象,进行仿真分析。直线轮廓误差和直线轮廓误差绝对值仿真结果分别如图16、图17所示。由图16和图17可以看出,以直线轨迹作为参考轨迹时,比例微分交叉耦合控制产生的轮廓误差明显小于传统比例微分控制。
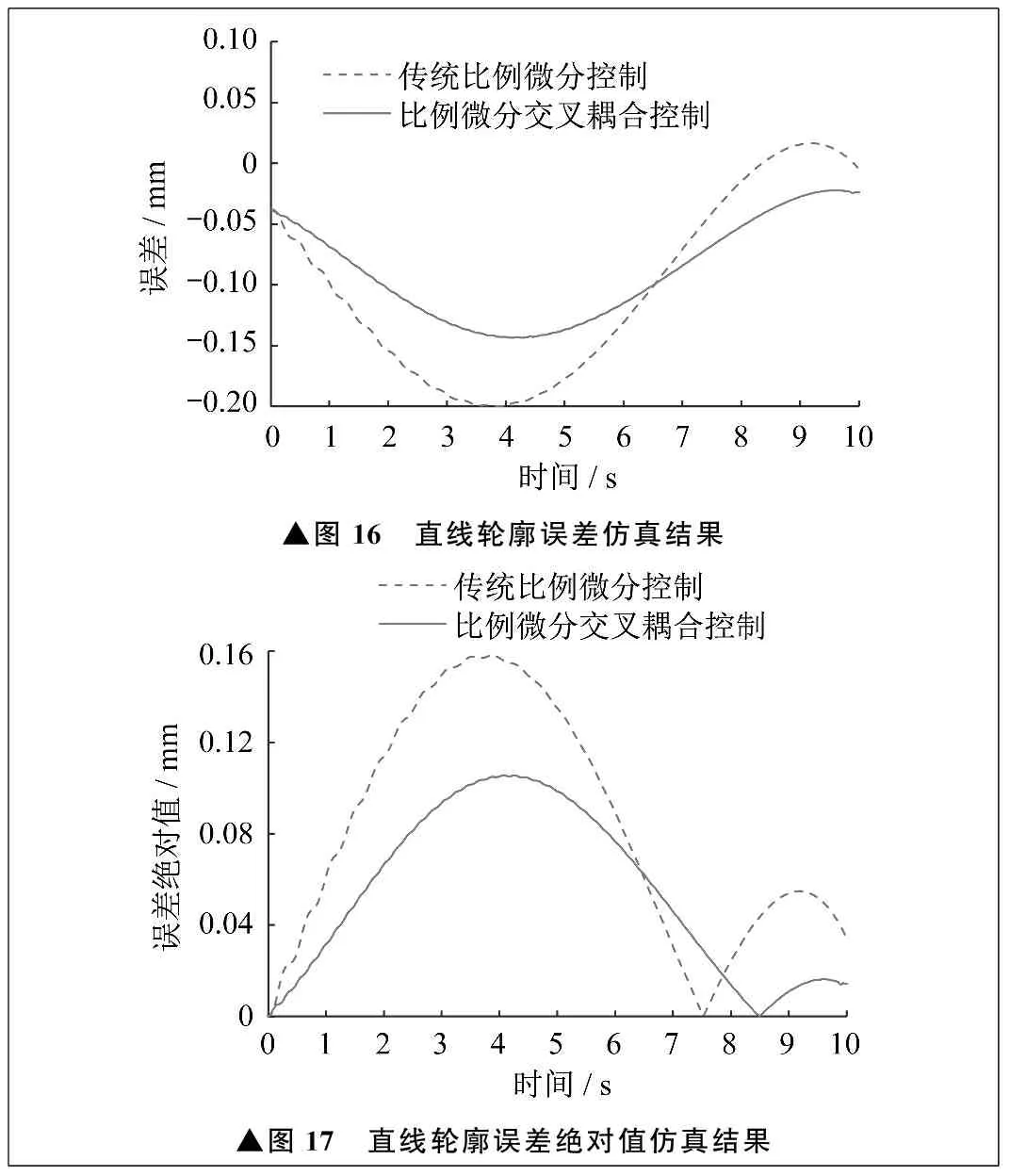
▲图16 直线轮廓误差仿真结果▲图17 直线轮廓误差绝对值仿真结果
7 结束语
笔者设计了一种新型坐卧式下肢康复机器人,可以使患者在冠状面与矢状面内运动。通过建立连杆模型,进行运动学分析,并求解速度雅可比矩阵。针对脑卒中早期卧床患者,规划一条直线轨迹,建立轮廓误差模型,结合传统比例微分控制,设计基于轮廓误差的比例微分交叉耦合控制器,并进行仿真分析,验证相比传统比例微分控制的优越性。未来笔者将深入分析这一坐卧式下肢康复机器人的临床安全性与有效性。

