考虑元件参数不确定性的高压直流输电系统可靠性区间评估

李凌飞，许树楷，姬煜轲，辛清明，侯婷，李岩，傅闯，赵晓斌，罗炜，黄莹

(1.直流输电技术国家重点实验室(南方电网科学研究院)，广州510663；2.中国南方电网有限责任公司，广州510663)

0 引言

高压直流(high voltage direct current，HVDC)输电系统在运行过程中具有损耗小、稳定性高、运行可靠和经济性高等优势而广泛应用于大容量、远距离电力输送[1-4]。近年来，我国大容量远距离电力输送需求不断增加、可再生能源大量接入以及能源互联网持续发展等，均给HVDC输电系统的可靠性提出了更高要求[5-7]。因此，准确评估实际HVDC输电工程的可靠性对电力系统安全稳定运行具有重大意义[8-9]。

实际HVDC输电工程中，元件数目众多，可靠性数据规模大，而数据录入时难免有误差，导致元件可靠性参数的统计结果带有一定的不确定性，从而影响HVDC输电系统可靠性评估结果的准确性，最终可能对未来电网的规划和运行造成影响[10]。目前，国内外很多学者针对元件可靠性参数不确定性对可靠性评估的影响进行了一些研究，主要有模糊数学法[11,12]、区间分析法[13-15]等。

模糊数学法是用模糊集来表示参数的不确定性，文献[16]将系统可靠性输入数据用模糊集来表示，进而得到可靠性指标的波动范围。针对如何选择有效模糊集的难点，文献[17]提出了用未确知有理数表示原始元件可靠性参数的方法，为处理参数不确定的电力系统可靠性评估提供了新思路。但是，有理数初值的选取以及计算精度和计算量等方面仍面临巨大挑战。

区间分析法[18]可以充分刻画元件参数不确定性，广泛运用于电力系统元件可靠性参数存在不确定性的研究中[19]。文献[20]针对配电网中元件原始参数不确定性问题，将原始参数用区间表示，利用区间分析法求解出参数变化对可靠性指标的影响。文献[13]提出大规模配电系统区间可靠性分析方法，解决了配电系统可靠性参数存在不确定因素时的可靠性评估，证明了区间可靠性评估算法是一种优越的灵敏度分析工具。虽然区间分析为解决元件参数不确定性的电力系统可靠性评估提供了有效途径，但是，区间计算得到的结果过于保守，尤其是在长计算链中，可能导致“区间爆炸”[21]，使可靠性评估结果失去参考价值。

针对区间计算结果过于保守问题，文献[22]将仿射算法引入输电网可靠性区间评估，算例结果表明，仿射算法有效解决了区间运算结果过宽的问题，得到更精确的可靠性指标。文献[23]为克服区间最小路法在含分布式电源配电网可靠性分析中过于保守的不足，通过将仿射算法和最小路法相结合，计及不确定变量之间的相关性，从而有效缩减可靠性指标的取值范围，在工程实际的应用中更显优势。

HVDC输电系统的元件可靠性参数的不确定性会影响其可靠性评估结果的准确性，然而，目前考虑元件可靠性参数不确定性的HVDC输电系统可靠性评估的模型和方法还未得到充分地研究。

因此，为了分析元件可靠性参数不确定性对HVDC输电系统可靠性的影响，迫切需要建立可靠性区间评估模型。首先，本文用区间数来表征元件可靠性参数的不确定性，推导了HVDC系统可靠性指标的区间算术表达式，建立了可靠性区间评估模型；然后，将仿射算术引入HVDC输电系统的可靠性区间评估以改善区间运算过于保守的问题；最后，本文使用一个典型的双12脉波接线的HVDC输电系统测试了所提的模型和方法。计算结果表明，该方法可以刻画元件参数不确定对HVDC输电系统可靠性评估的影响，且能够有效地解决区间计算结果过于保守的不足，同时也是一种高效的薄弱元件分析工具。

1 区间算术与仿射算术的数学模型

1.1 区间算术及其应用

20世纪60年代，摩尔提出区间算术(interval arithmetic, IA)，通过把数据存储为区间形式然后对区间进行运算。区间运算不仅将区间参数包含在整个计算过程中，还可描述结果的波动范围，广泛运用在处理有限精度计算中的不确定性问题领域[24]。

1.1.1 区间运算法则及其局限性

(1)

(2)

(3)

(4)

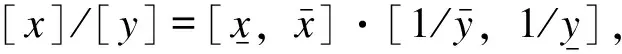
(5)

式中C为常数。

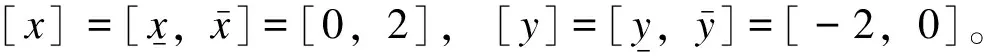
综上，IA可以用区间变量的概念来刻画参数不确定性对结果的影响，计算过程简单，在实际应用中具有重要的意义；但IA仍有一定局限性：1)区间运算得到的结果往往比实际应得区间大得多，过于保守，导致得到的区间结果参考价值不大；2)区间运算不能考虑区间数之间的相关性。若在电力系统可靠性计算中不考虑区间运算的“相关性”，将会导致计算结果呈现区间爆炸[23]。因此，为了解决区间结果过于保守的问题，本文在HVDC输电系统可靠性区间评估中引入了仿射算法。

1.2 仿射算术

1.2.1 仿射算术原理

仿射算术(affine arithmetic, AA)通过引入不同不确定变量之间的相关性系数，在一定程度上解决了区间运算结果保守性问题[25]。因此，本文将仿射算术引入HVDC输电系统可靠性区间评估来改善区间运算结果过于保守的问题。

不确定性变量用仿射形式的线性多项式可以表示为：

(6)

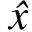
仿射算术(AA)是针对区间算术(IA)存在不足而提出的，因此两者可以等价转换。

假设有IA形式的变量[x]=[xmin,xmax]，则可以转化为等价的AA形式的变量表示，如式(7)所示。

(7)

式中：x0=(xmin+xmax)/2；x1=(xmax-xmin)/2；ε1∈[-1,1]。

(8)

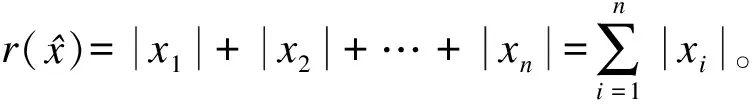
(9)

(10)

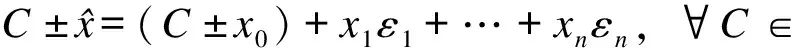
(11)

(12)

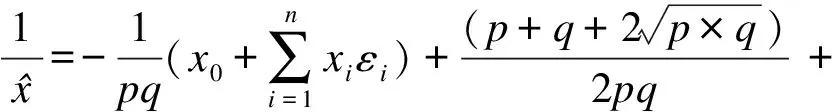
(13)

式中：

(14)

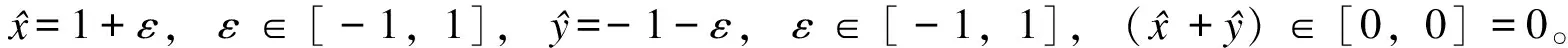
此外，如式(12)所示，当两个仿射形式的数相乘时将会出现噪声元二次项，结果为非仿射形式，将不满足仿射变量的定义，无法运算。因此，本文对非仿射形式进行仿射近似，进而得到仿射形式的数，再进行下一次运算。

1.2.2 仿射近似

仿射近似就是采用数学逼近的策略将非仿射形式近似等价为仿射形式。常用的近似方法有切比雪夫、面向高阶噪声相关性的改进仿射算法和简单近似估计[26]。前两种方法均考虑了变量之间高阶噪声元的相关性，近似效果较好，但计算量会随着精度的提升而剧增；后者既保持了较好的精度且计算量较少，是两者较好的折衷，有研究表明，在最糟糕的情况下其误差为切比雪夫近似方法的4倍[26]。

本文采用简单近似估计法引入一个新的噪声元εn+1，εn+1∈[-1,1]，将式(12)中的非仿射形式等价为：

(15)

两个仿射形式变量相乘时的简单近似估计仿射形式为：

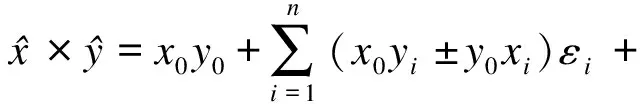
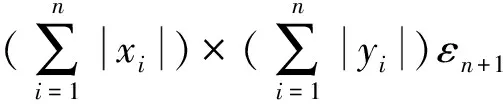
(16)

2 高压直流输电系统子系统可靠性模型

本文以如图1所示的双12脉波接线HVDC系统为例进行建模分析。

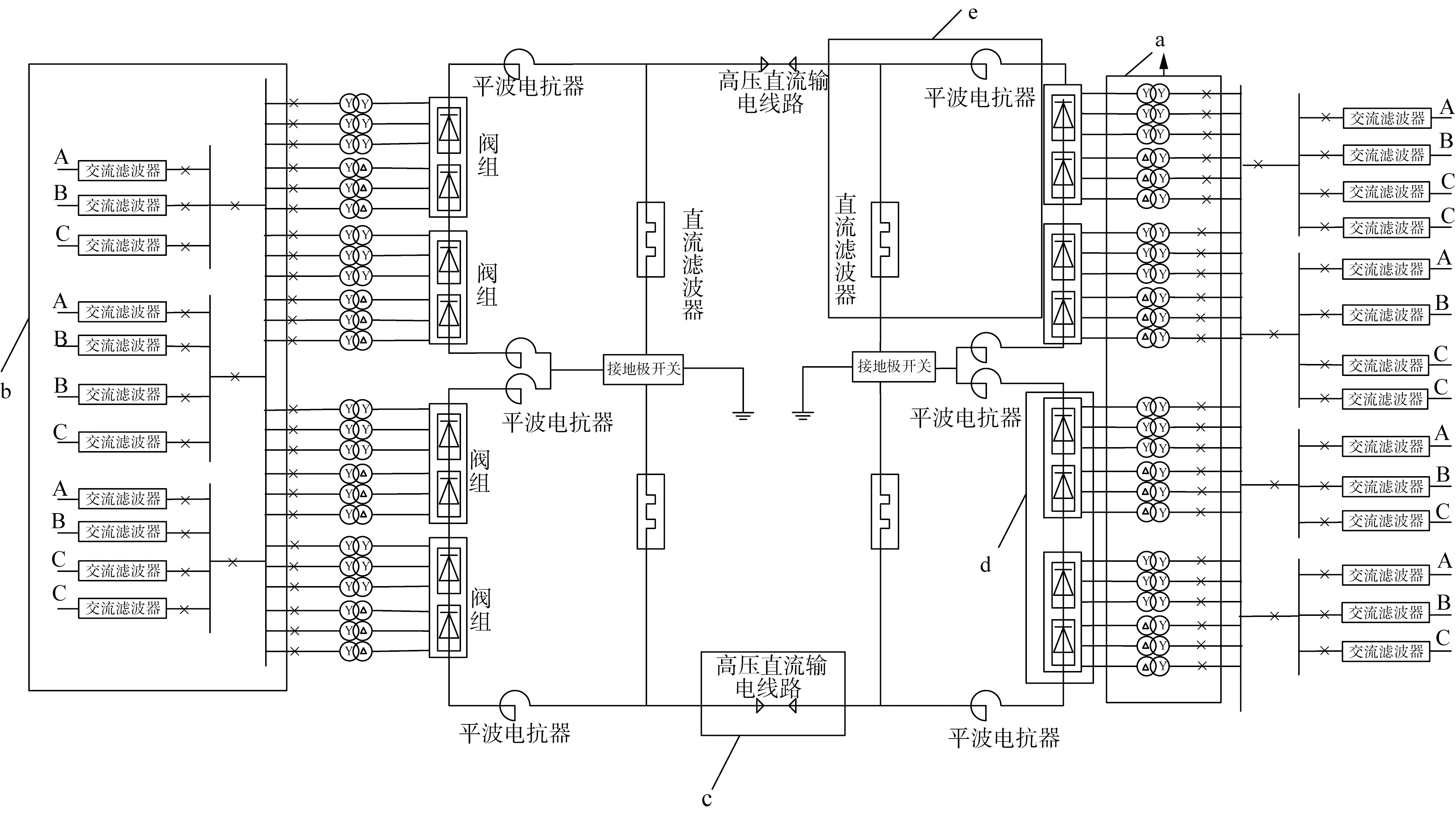
a—换流变压器子系统 b—交流滤波器子系统 c—直流输电线路子系统 d—阀组子系统 e—直流场子系统

高压直流输电系统元件数目众多，结构复杂，为了提升计算效率，本文采用文献[27]中的HVDC输电系统可靠性评估模型和方法。首先，基于分而治之的策略，将HVDC输电系统划分为若干个子系统并建立各个子系统的可靠性评估模型。然后根据子系统之间的可靠性逻辑关系，组合得到整个系统等值可靠性评估模型。

双12脉波接线的HVDC输电系统主要可以划分为五个子系统，分别为：交流滤波器子系统(AC filter subsystem, ACFS)、换流变压器子系统(converter transformer subsystem, CTS)、直流输电线路子系统(DC line subsystem, DCLS)、直流场子系统以及阀组子系统。本文基于状态枚举法以双12脉波接线的HVDC输电系统为例来建立各个子系统可靠性评估模型，下面以换流变压器子系统为例。

2.1 换流变压器子系统

图1中的a模块表示换流变压器子系统，系统每一极有12台换流变压器，由6台Y/Y和6台Y/△接线换流变压器构成，且平均分布在单侧单极每个阀组上。根据双12脉波接线的HVDC输电系统的结构和运行特点，与每个换流阀连接的3台Y/Y与3台Y/△接线换流变压器可等效为1个元件，由串联元件失效原理，可得：

(17)

(18)

式中：λiY和μiY、λi△和μi△分别对应第i个Y/Y、Y/△型接线换流变压器的故障率和修复率；λsY和μsY、λs△和μs△分别为对应3台Y/Y、Y/△接线的换流变压器的等值故障率和修复率，下标s为串联。

通常换流变压器子系统按换流阀分组接线类型单极单侧整体备用，在枚举换流变压器故障事件时，若考虑备用，则需先检查故障设备与备用设备的型号以及接线方式是否匹配，以确定是否可换。若满足替换条件，按备用启用最优顺序进行提替换，用投入的换流变压器的安装率代替式(17)和(18)中故障换流变压器的修复率即可。

2.2 系统可靠性评估模型

同理，直流场部分中的极控、备用电源、平波电抗和直流滤波器等也可直接等效为两状态元件。其它几个子系统的元件停运率建模也类似，具体可以参见文献[27]。基于元件停运率模型，再得到每个子系统不同容量状态的指标。最后，通过整合各个子系统相同容量状态的指标，得到整个系统不同停运容量对应的概率和频率指标。系统等值可靠性逻辑框图如图2所示。

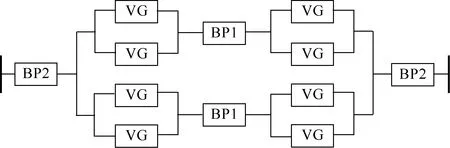
图2 高压直流输电系统可靠性逻辑框图

图2中，BP1指单极元件的组合，包括单极单侧直流滤波器、平波电抗器、极控和直流线路等元件；BP2指整流侧和逆变侧的双极元件，主要包括交流滤波器子系统、站控和交流场；VG指单侧单极换流单元，即单极单侧单个12脉波阀组对应的换流阀、换流变压器和断路器等元件的组合。

3 基于仿射算法的高压直流输电系统可靠性区间评估

根据HVDC输电系统子系统划分的特点，首先基于仿射算术推导系统可靠性指标仿射区间数计算公式。然后，结合状态解析法建立基于仿射算术的HVDC输电系统可靠性区间评估模型，最后，进行可靠性区间评估。

3.1 串联系统仿射型可靠性评估模型

假设n个元件组成的串联系统如图3所示。

图3 n个元件串联系统

由串联系统元件失效原理，可得到n个元件串联系统的等值可靠性参数如下：

(19)

(20)

(21)

式中：λi和μi分别为第i个元件的故障率和修复率，λs、rs和Us分别为串联系统等值的故障率、修复时间和不可用度。

根据1.2节介绍的仿射算术，下面结合HVDC输电系统特点，利用AA推导串联系统的仿射形式等值参数。第i个元件的故障率λi和修复率μi分别用仿射数表示为：

(22)

(23)

(24)

(25)

(26)

3.2 并联系统仿射型可靠性评估模型

假设n个元件组成的并联系统如图4所示。

图4 n个元件并联系统

由并联系统元件失效原理，可得到n个元件串联系统的等值可靠性参数如下。

(27)

(28)

(29)

式中λp、μp和Up分别为并联系统等值的故障率、修复时间和不可用度。

同理，可得到n个元件并联系统仿射型等值可靠性参数的计算公式如下。

(30)

(31)

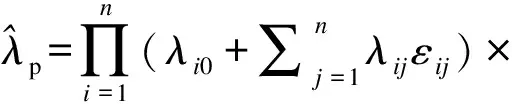
(32)

综上，在串并联系统仿射型等值可靠性参数计算中，不可用度的计算过程会出现两个仿射数相乘，产生非仿射形式结果。针对仿射数相乘出现的噪声元二次项的问题，本文利用式(15)将非仿射形式通过简单近似估计转化为仿射形式，再进行下一次运算。因此，利用串联系统仿射型可靠性评估模型，再结合HVDC输电系统状态解析法，由整个系统等值可靠性逻辑框图便可以得到HVDC输电系统可靠性区间评估模型，计算流程图如图5所示。

图5 可靠性区间评估流程图

4 算例分析

4.1 算例简介

本文以双12脉波接线的HVDC输电系统为测试系统，进行可靠性区间评估分析。

双12脉波接线的HVDC输电工程如图1所示，其等值可靠性逻辑框图如图2所示，各元件原始参数如表1所示[27-29]。为计及元件原始可靠性参数的不确定性，算例中假设元件可靠性参数在其确定数值±10%范围内变化[30]。

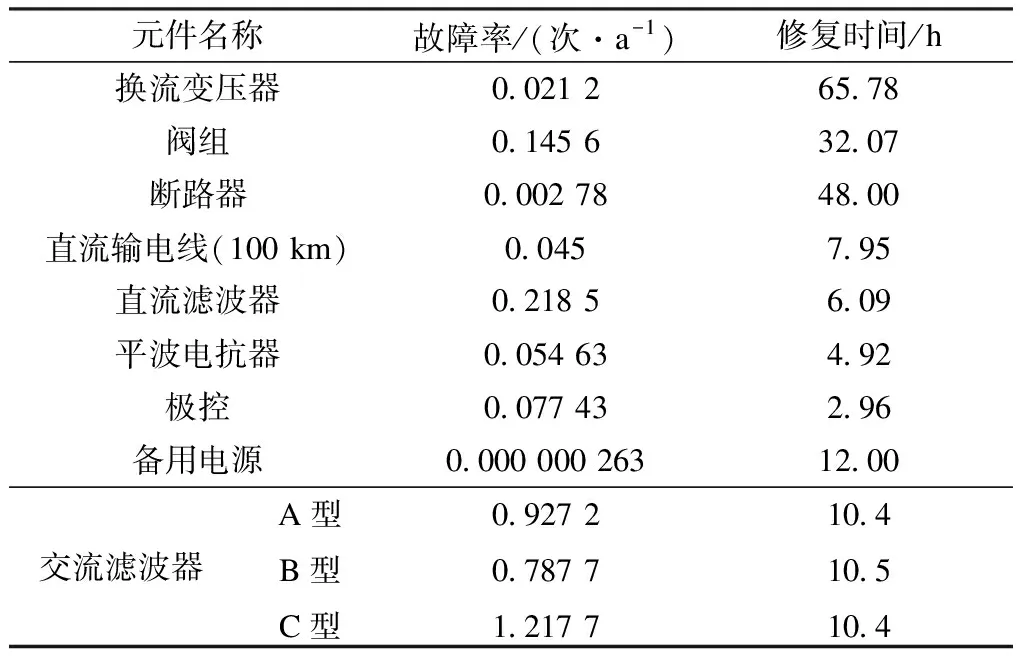
表1 双12脉波接线特高压直流输电系统可靠性参数

本文采用状态解析法计算系统可靠性指标，将各个子系统的故障事件枚举到了五阶，并以该指标值作为参考值。然后利用本文提出的可靠性区间评估方法计算参数不确定性对可靠性指标的影响，来验证本文所提模型和方法的合理性和有效性。

4.2 可靠性评估结果

采用状态解析法算得双12脉波接线的HVDC输电系统可靠性指标如表2所示，系统不同停运容量对应的概率和频率指标计算结果如表3所示。

表2 双12脉波接线的高压直流输电系统可靠性评估指标

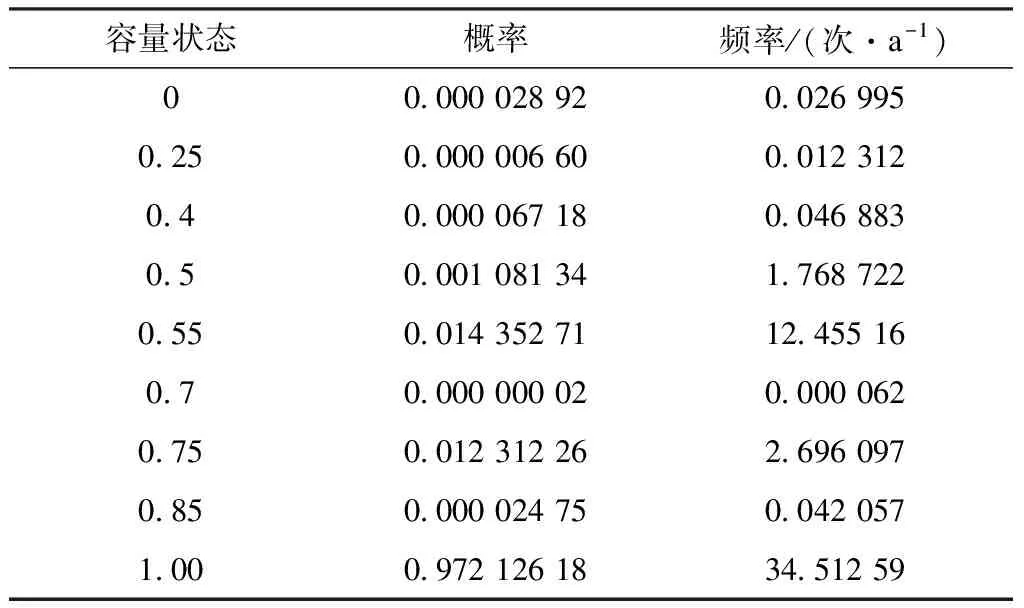
表3 双12脉波接线的高压直流输电系统容量状态对应概率和频率计算结果

由表2可知：系统强迫能量不可用率为0.010 155、单极强迫停运率为1.768 722次/a、双极强迫停运率为0.026 995次/a。在本文后续算例分析中，上述系统指标结果将作为参考值来验证本文模型和方法的正确性。

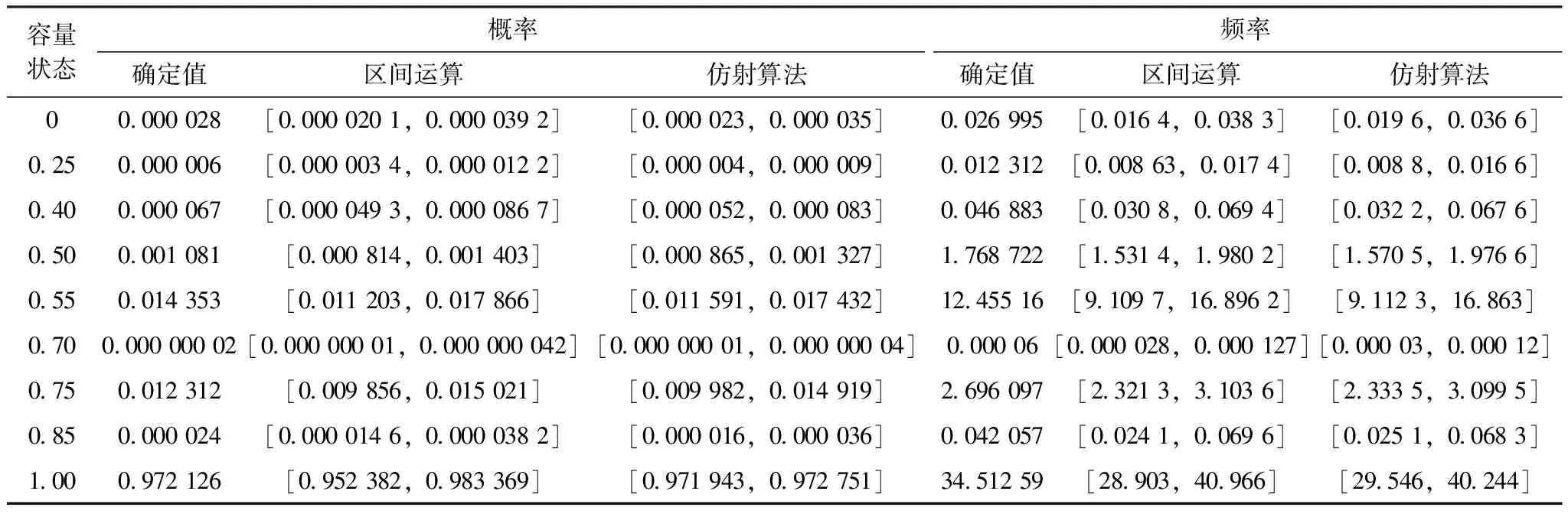
表5 双12脉波接线高压直流输电系统容量概率、频率区间结果

4.3 基于仿射算术的双12脉波接线的高压直流输电系统可靠性区间评估

为了验证本文提出的考虑元件可靠性参数存在不确定性的HVDC输电系统可靠性区间评估方法的合理性和有效性，以下分别计算了不考虑设备冗余时系统的主要指标和各容量状态的概率和频率，结果如表4—5所示。

表4 双12脉波接线高压直流输电系统可靠性区间指标

由表4—5可知：计及元件可靠性参数不确定性得到的区间结果都包含了对应的确定值，证明本文所提考虑元件参数不确定性的HVDC输电系统可靠性区间评估模型和方法的正确性。同时，为了量化参数不确定性对可靠性评估的影响，本文将元件可靠性参数不确定性对系统可靠性评估结果的影响度定义为区间值的变化范围与确定值的比值，如表4中，系统强迫能量不可用率的确定值为0.010 155，采用仿射算法得到的区间值为[0.008 2, 0.012 3]，其上下界之差Δ2为0.004 1。则当元件可靠性参数在其确定数值±10%范围内变化时对系统强迫能量不可用率的影响度为40.3%。

同理，可计算相同条件下对系统单极强迫停运率和双极强迫停运率的影响度分别为22.9%和62.9%。由计算结果可以发现，系统双极强迫停运率的影响度最大。这可能是因为元件故障状态对应的不可用率区间相对于其确定值的比值要大于正常状态对应的可用率的比值，而造成双极强迫停运的系统状态中故障元件的数目较多，且双极强迫停运率的计算中含有更高比例的不可用率区间。因此，双极强迫停运率的区间扩张程度(即影响度)更大。

此外，本文将区间运算和本文方法(仿射算法)进行了对比，如表4中，系统强迫能量不可用率的确定值为0.010 155，区间运算得到的区间值为[0.008 03, 0.014 37]，其上下界之差Δ1为0.006 34，而利用仿射算术得到的区间值的上下界之差Δ2为0.004 1。显而易见，利用仿射算法得到的区间值为包含确定值的更紧密区间，其结果与理论分析一致，结合本文1.1节区间相关性问题计算的例子，证明了在HVDC输电系统可靠性区间评估引入仿射算术可以有效地抑制区间扩张，得到有效的区间解。

4.4 薄弱元件分析

为了分析元件故障率变化对系统强迫能量不可用率的贡献大小(简称薄弱元件识别)，及验证本文方法在薄弱元件识别的优越性，设置了以下算例。本文薄弱元件识别主要对换流变压器，平波电抗器和交流滤波器等元件进行分析，算例中假定各元件故障率变化范围为λnew∈[0.5λ,5λ]。采用本文方法计算HVDC输电系统可靠性区间评估指标，考虑和不考虑交流滤波器冗余的结果分别如表6—7所示。

表6 双12脉接线高压直流输电系统元件故障率对强迫能量不可用率的贡献分析(交流滤波器冗余)

表中，贡献值为对应的元件对系统能量不可用率的影响在表中所列举各元件对系统能量不可用率影响之和中所占的比例。由表6和表7可知，无论交流滤波器有无冗余，直流输电线路和平波电抗器故障率变化对系统不可用率的贡献都较小，其原因是直流输电线路和平波电抗器元件数量相对较少，故其故障率变化对系统不可用率贡献较小；在交流滤波器没有冗余时，交流滤波器对系统不可用率指标的贡献很大，而考虑冗余时，换流变压器和阀组对系统不可用率指标的贡献很大，交流滤波器对系统不可用率指标的贡献和直流线路差不多。这主要是因为交流滤波器数量较多，在没有冗余时其故障率变化对系统不可用率影响较大，而考虑冗余时将有效提高系统可靠性，以上结果与理论分析相符合。

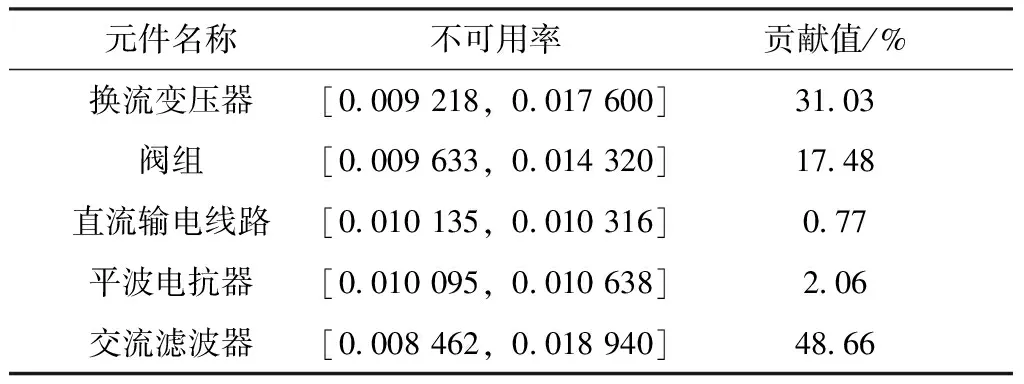
表7 双12脉接线高压直流输电系统元件故障率对强迫能量不可用率的贡献分析(不考虑交流滤波器冗余)

通过以上薄弱元件分析，便可得到不同元件对系统不可用率贡献的相对大小，为提升可靠性提供一定的参考。其次，因为只需要一次区间运算就能得到不同元件故障率变化对系统不可用率的贡献值，效率较高，故本文方法在薄弱元件识别的计算效率上具有很大优势。

5 结语

本文研究了区间算法在HVDC输电工程可靠性评估中的应用，计及元件可靠性参数的不确定性，建立了考虑可靠性参数不确定性的元件停运率区间模型，通过对双12脉波接线的HVDC输电系统进行可靠性区间评估，验证了本文模型的合理性和有效性。

由算例结果分析可得，本文可靠性区间评估方法可以刻画元件参数不确定性对HVDC输电系统可靠性评估的影响，避免了对元件可靠性参数本身准确性的过度依赖，并有效地解决了区间计算结果过于保守的问题，且该方法也是一种薄弱元件分析工具。在元件可靠性参数不确定的情况下，该方法有利于工程人员把握系统的可靠性水平，能够为实际的HVDC输电工程的规划设计的决策提供量化参考依据。