OpenSEES对钢筋混凝土结构滞回的模拟

董 浩，杨 露，林 钢，赵威中，白国明

(1.中建三局集团有限公司，湖北 武汉 430000；2.四川金陵润鸿建设工程有限公司，四川 成都 610000)

0 前 言

对于目前建筑结构的发展，如何较可靠地得到结构在强震作用下的非线性反应是结构设计领域的重要课题。需要通过不断的试验得到更多更可靠的数据为结构设计做依据，虽然通过构件模型试验直接获取钢筋混凝土构件特性的方法已经成熟，但是对于复杂结构，利用建筑结构的缩尺模型是无法得到可靠的动力特性数据，而且相当一部分结构是无法缩尺的，且成本也不允许。因此，使用有限元软件模拟就显得十分重要，特别是通过动力非线性分析以弥补模型试验的不足，成本较低，是一种行之有效的方法。

OpenSEES[1]是由美国国家自然科学基金(NSF)资助、西部大学联盟“太平洋地震工程研究中心”(Pacific Earthquake Engineering Research Center，简称PEER)主导、加州大学伯克利分校为主研发而成的、用于结构和岩土方面地震反应模拟的一个较为全面且不断发展的开放的程序软件体系，其拥有非常突出的结构非线性处理能力。程序提供了6种混凝土单轴本构模型和3种钢筋单轴本构模型。用户也可以根据需要自己定义新材料以及二次开发，但对于大多数人来说二次开发难度太大。通常直接使用软件提供的材料参数进行分析，但OpenSEES提供的各种材料本构的使用性有待考察与证实，在混凝土本构方面：李正达[2]对OpenSEES提供的concrete01、concrete02、concrete03模型进行对比总结，并通过混凝土框架进行动力非线性分析，对比模型的计算精度；陈伟[3]对比分析了OpenSEES中提供的6种混凝土单轴本构，并对一榀八度区二级框架进行了大震下的非线性动力分析；赵金钢[4]对OpenSEES中6种混凝土本构模型进行了原理和具体参数取值的全面汇总，并对钢筋混凝土柱进行了拟静力分析；冷巧娟[5]研究了钢筋在混凝土中的滑移连接本构并对已有的2根既有钢筋混凝土构件进行有限元模拟；吴荒龙[6]基于OpenSEES的钢筋本构关系进行了二次开发；赵璧归[7]通过HRB400钢筋本构对比分析了OpenSEES 3种钢筋本构，并通过试验进行了滞回的模拟。

因此，本文汇总了OpenSEES中所提供的材料本构模型参数设置，然后针对既有的钢筋混凝土梁柱节点进行有限元模型的构建，通过数值模拟结果与试验结果对比，研究本构模型在模拟钢筋混凝土结构动力非线性分析的准确性，通过钢筋本构和零长度单元实现滞回曲线中的刚度退化、捏缩滑移等现象。

1 钢筋材料本构模型

1.1 steel01模型

steel01模型是最常用的双折线(Bilinear)模型，未能考虑钢筋在循环荷载下的疲劳和刚度退化。众所周知，钢筋在反复作用下的包辛格效应[8]对结构的滞回特性有着十分重要的影响，双折线模型认为加载和卸载路线均为直线，卸载刚度为初始刚度，没有刚度退化，应力应变关系简单，仅以初始模量、屈服强度与强化率控制，本构曲线如图1所示，分为两个阶段：弹性阶段和强化阶段。

图1 steel01应力-应变曲线

应力-应变曲线表达式为：

弹性阶段：σ=E0ε(|ε|≤fy/Es)

(1)

强化阶段：σ=fy+Esε(|ε|≥fy/Es)

(2)

式中，fy为钢筋屈服强度；E0为钢筋初始模量；Es为强化段钢筋模量。图1中，b表示钢筋强化率。

如图2所示：模型加卸载曲线为直线，没有考虑钢筋疲劳与刚度退化，与现实加载差距较大，无法准确表示材料性能。因此，该模型更适用于构件静力加载中承载力的模拟，不适于模拟反复加载下构件的滞回性能。

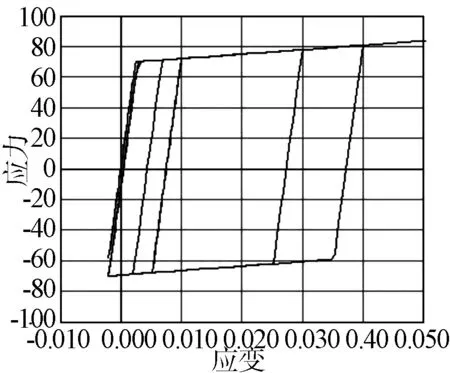
图2 steel01模型的滞回规则

OpenSEES中，steel01模型参数规格如下：

1.2 steel02模型

Steel02模型是pinto钢筋模型[9]，是由Menegotto与Pinto(1973年)提出，模型表达方式简洁，在模拟结果方面与钢筋材料试验结果吻合性好，具有很好的数值稳定性，可以通过过渡曲线曲率参数R调整钢筋的包辛格效应[8]，但该模型同样没有考虑钢筋的疲劳以及受拉时钢筋截面缩小的特征。本构曲线如图3所示，分为3个阶段：弹性阶段、强化阶段、滞回阶段。

图3 steel02应力-应变关系

曲线有初始弹性模量E0转向模量E1(E1=b×E0)，式其中b为钢筋的硬化系数。在任意应变的历史下，应力-应变关系表达式的确定仅取决于当前受力状态下的反向加载点(εr，σr)和参数R。

Steel02 模型应力-应变(σ-ε)关系曲线表达式为：

(3)

式中，σ*与ε*分别为归一化的应力应变，分别按以下公式计算：

(4)

(5)

(6)

式中，R0为初始加载时曲线的曲率系数；a1与a2为钢筋在往复加载时钢筋的曲率退化系数，ξ为钢筋在加载史上最大的应变的参数：

(7)

式中，εm为加载史上最大的应变，εy为钢筋的屈服应变。

如图4所示，Steel02模型模拟了钢筋的辛格效应[8]，是通过曲线过度参数R使曲线在反向应变时刚度减小，模拟出包辛格效应[8]，不过该模型依然没有考虑钢筋的疲劳和损伤累积，参数R根据用户手册[1]过度参数R的取值如下($R0=between 10 and 20，$cR1=0.925，$cR2=0.15)其中随着R0的增大，曲线捏缩越不明显，建议取值15；cR1越大捏缩越明显，同时骨架曲线提前出现下降段；cR2越大捏缩效果越不明显。

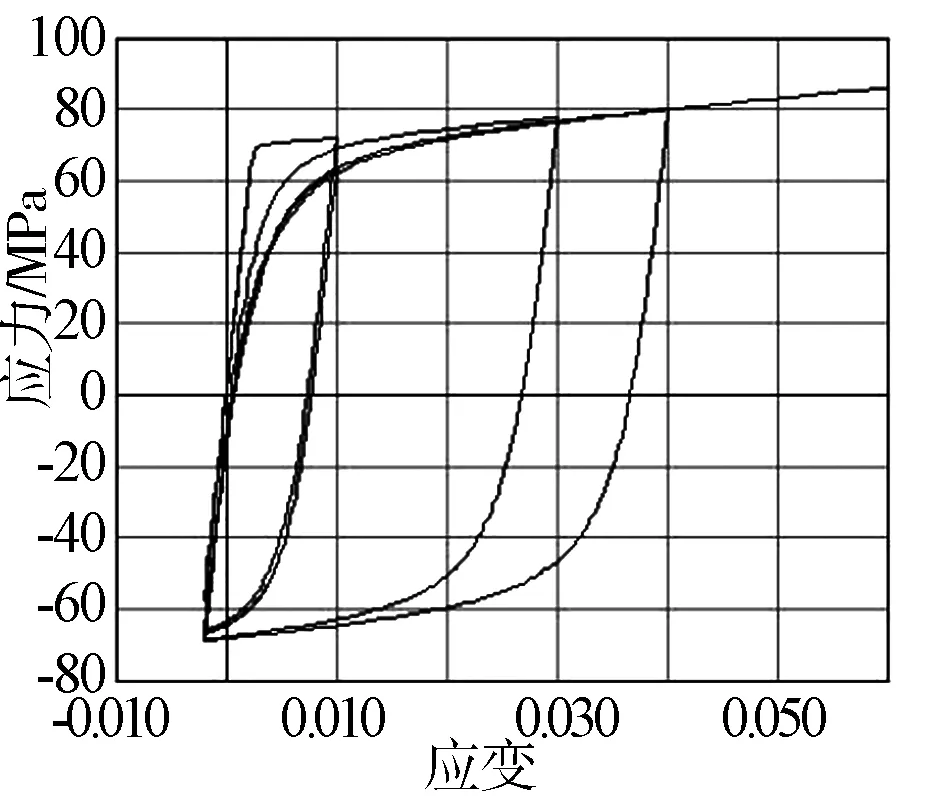
图4 steel02模型的滞回规则

在OpenSEES中steel02模型引用格式如下：

2 混凝土材料本构模型

OpenSEES中为混凝土提供了6种单轴受力的混凝土材料本构，根据赵金钢[4]对于混凝土本构模型对结构滞回的模拟对比，其中Concrete01、Concrete02、Concrete03、Concrete07，可以较好地体现出钢筋混凝土结构在往复受力下的捏缩效应和滞回特性，但其中Concrete03、Concrete07本构复杂，计算不容易收敛。Concrete02混凝土本构易收敛，方式简单，在滞回模拟方面拥有足够的精度。

Concrete02中受压行为的本构关系是采用Scott修正的Kent-Park模型，同时该模型考虑了箍筋的约束作用，该本构分为3个区段：上升段、下降段和平台段，表达式如下：

上升段(εc≤ε0)：

(8)

下降段(ε0≤εc≤εu)：

(9)

平台段(εc>εu)：

(10)

其中：

ε0=0.002K

(11)

(12)

(13)

在OpenSEES中Concrete02模型引用格式如下：

图5 Concrete02模型示意图

3 钢筋的黏结滑移本构模型

在实际施工的钢筋混凝土结构中由于施工质量的原因会导致节点处钢筋锚固不足或混凝土强度存在差异，导致节点处发生滑移，在OpenSEES[1]中有专门的零长度单元来模拟节点处的滑移变形：①BARSLIP Material这种材料可以精确模拟循环加载时在构件节点处由于钢筋滑移和混凝土开裂所引起的构件刚度退化和强度退化等现象；②Bond-SP01 Material可以模拟节点处钢筋的应力渗透现象(节点处钢筋还没有整体滑移)所引起的构件的强度和刚度的变化[10]。因为在试验中钢筋发生整体滑移的可能性不大，因此采用Bond-SP01 Material的材料模型，该材料通过定义钢筋的屈服强度带入下式：

(14)

计算出屈服强度下钢筋的滑移量，再由Su=(30～40)×Sy计算出极限滑移量。

在OpenSEES中Bond_SP01模型(见图6)引用格式如下：

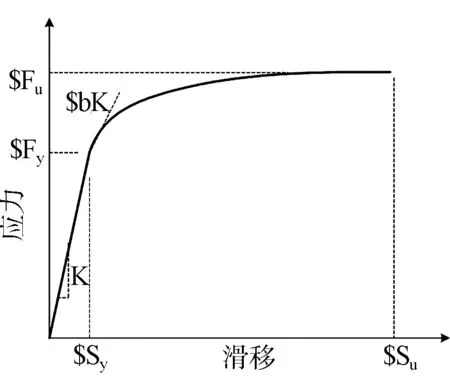
图6 Bond-SP01本构模型

图7 R取1.0与0.6的捏缩对比

4 采用的梁柱模型

OpenSEES中提供了3种梁柱模型：弹性梁柱模型、两端塑性铰模型、非线性梁柱模型，根据齐虎[10]对纤维模型的研究发现，采用非线性梁柱模型计算精确度更高，如果再与零长度构件一起使用可以达到精确模拟梁柱构件实际变形的目的。

5 有限元模拟

本文对清华大学开展的钢筋混凝土框架梁柱边节点拟静力试验进行了数值模拟，并与试验结果做了对比，选用的试验构件参数选自文献[11]，设计参数如图8。

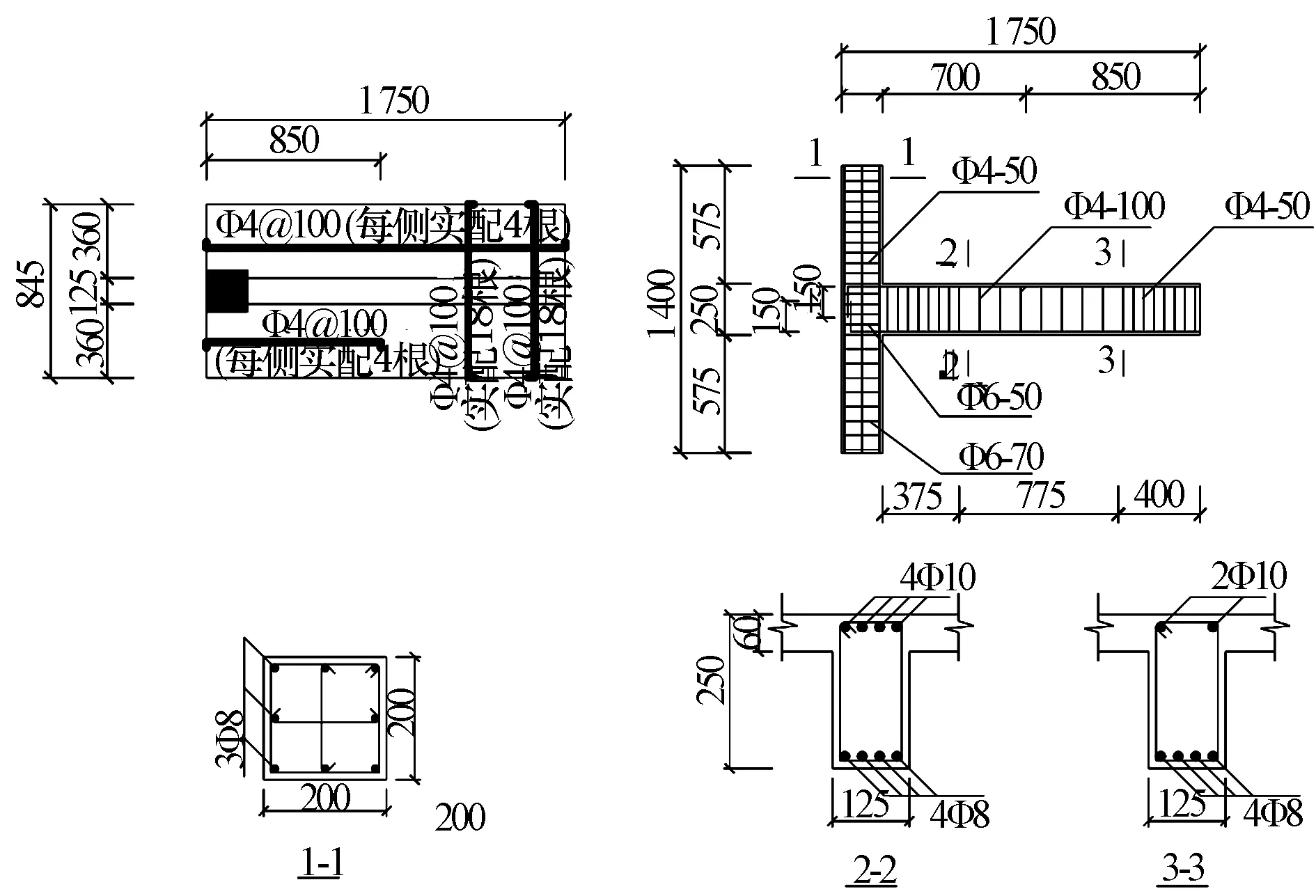
图8 设计参数(单位：mm)

钢筋各项指标如表1所示。

表1 钢筋强度指标

混凝土轴心抗压强度为43.4 MPa。由于OpenSEES无法建立箍筋，采用约束混凝土代替箍筋，核心区混凝土轴心抗压强度增大40%，当变形很大时保护层混凝土会剥落，在建模时保护层混凝土屈服后强度稍低一些。

为了模拟节点处的钢筋滑移变形，在梁柱节点处添加零长度单元(并非正在的零长度OpenSEES在分析时是取其长度为单位长度)，并赋予Bond_SP01的材料性质。实验结果和模拟结果如图9。

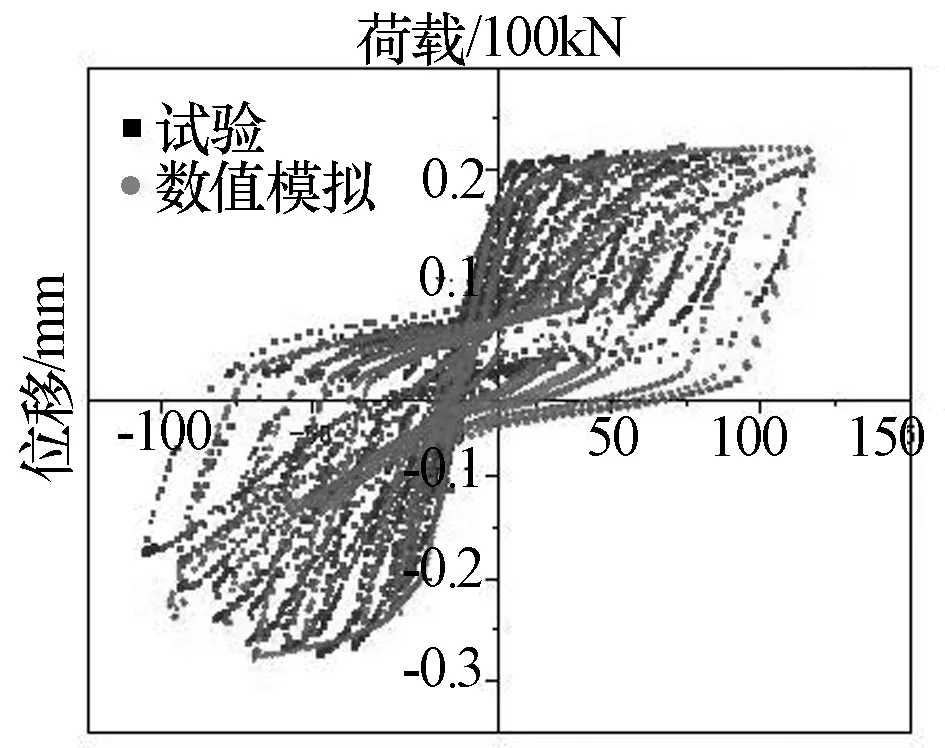
图9 试验结果与数值分析结果比较

从图9中的对比可以看出数值模拟结果与试验结果模拟较好，由于OpenSEES是基于平截面假定的，所以卸载刚度较大，同时利用钢筋滑移单元模拟捏缩现象，对于混凝土开裂滑移无法模拟，因此，滑移段刚度较试验结果偏大。

6 材料本构对有限元模拟的影响

6.1 约束混凝土对结果的影响

如图10所示，由对比可知不考虑混凝土约束作用的有限元模拟结果比实验结果明显较低。

图10 混凝土不考虑约束有限元模拟与试验结果对比

6.2 不考虑滑移对结果的影响

如图11对比可知，当结构不考虑滑移，有限元模拟的滞回过于饱满，无法体现结构破坏模式，但对结构峰值荷载的模拟依旧十分吻合。

图11 不考虑滑移有限元模拟与试验结果对比

6.3 采用不考虑包辛格的钢筋本构对结果的影响

如图12对比，采用无包辛格效的钢筋本构滞回曲线与试验结果拟合较好，捏缩段刚度稍稍增大，滞回环稍饱满，基本可以反应结构性能，对于复杂结构为了计算收敛快速可以采用此钢筋本构。

图12 钢筋不考虑包辛格效应的有限元模拟结果与试验结果对比

7 结 论

在钢筋混凝土结构的有限元模拟中，若忽略其中混凝土所受的约束、钢筋滑移以及包辛格效应，则有限元的计算结果与试验结果将会存在差距。通过本文对比可知：①不考虑混凝土约束作用的有限元模拟结果比实验结果明显较低；②当结构不考虑滑移，有限元模拟的滞回过于饱满，无法体现结构破坏模式，但对结构峰值荷载的模拟依旧十分吻合；③采用无包辛格效的钢筋本构滞回曲线与试验结果拟合较好，捏缩段刚度稍稍增大，滞回环稍饱满，基本可以反应结构性能，对于复杂结构为了计算收敛快速可以采用此钢筋本构。

[ID：013750]