集合约束下多智能体系统分布式固定时间优化控制
陈 刚 李志勇
分布式优化在多机器人系统、传感器网络、机器学习等领域应用前景广阔,因此成为了当前的一个研究热点[1-2].基于多智能体系统框架的各种分布式算法被相继提出并用于解决各类优化问题[3-16].文献[3]利用离散时间一致性和次梯度法求解无约束分布式优化问题.文献[4]采用分布式投影次梯度法解决带集合约束的优化问题.基于原始对偶最优解的鞍点特征,文献[5]设计分布式原始对偶次梯度算法,求解带等式和不等式约束的优化问题.文献[6]采用一种近似梯度算法求解无精确梯度信息的受约束分布式凸优化问题.文献[7]利用一种基于投影梯度的分布式分层算法求解受集合约束的大规模多簇优化问题.文献[8]应用一种分布式优化最小化方法来解决拉普拉斯正则化问题.利用连续时间动力学系统分析工具[9-16],分布式连续时间算法也得到广泛的关注.文献[10]采用一种基于零梯度和原理的分布式连续时间算法求解无约束优化问题.文献[11]给出一种分布式连续时间算法,使得智能体状态量收敛到约束集合内的最优一致值.基于拉格朗日乘子法和KKT (Karush-Kuhn-Tucker)条件,文献[12]给出一种求解带局部不等式约束的分布式连续时间优化算法.文献[13]采用基于神经动力学的分布式计算方法求解带全局耦合约束的凸优化问题.文献[14]采用分布式比例积分协议求解受约束最优化问题.文献[15]研究时变目标函数下的分布式无约束优化问题.
收敛速率是评价算法性能的重要指标之一.基于线性协议的分布式优化算法[3-16]仅实现渐近或指数收敛,理论上在时间趋于无穷时获得最优解,这导致实际应用中只能得到次优解.然而,一些实际应用需要快速求取优化解,例如燃料有限的宇宙飞船交会对接问题,能源系统的在线实时调度等问题.为加速算法的收敛速度,近年来分布式有限时间收敛算法得到广泛关注[17-20].基于分布式零梯度和优化算法[10]和有限时间一致性方法,文献[17]给出一种有限时间分布式一致性优化算法.文献[18]针对时变目标函数优化问题,提出一种基于二阶多智能体系统的分布式有限时间算法.文献[19]利用梯度符号信息,提出一种分布式有限时间优化算法.文献[17-19]仅考虑无约束优化问题.文献[20]提出的分布式有限时间优化算法能处理非一致梯度增益和集合约束.虽然有限时间控制拥有收敛速率快、干扰抑制性好、鲁棒性强等优点[21-23],但其收敛时间的上界取决于系统初始状态,且随着初始值的增大而增大.当系统初始状态未知时,收敛时间难以预先估计.
为克服有限时间控制的不足,文献[24]提出了固定时间稳定的概念,固定时间控制使得收敛时间的上界不依赖系统初始状态,仅与控制参数相关.分布式固定时间一致性算法已得到广泛研究[25-29].对于带约束的优化问题,分布式固定时间一致性算法往往不能直接用于求解.目前关于分布式固定时间优化算法还未得到广泛研究.对于无约束优化问题,文献[30]的分布式算法能实现智能体状态量的固定时间一致性,而最优解为渐近收敛.文献[31]利用分布式固定时间算法求解带等式约束的优化问题.
受现有研究的启发,本文利用时变增益法和固定时间投影法,提出一类新的分布式算法,用于求解集合约束下多智能体系统凸优化问题.提出的固定时间投影法既能处理智能体相同局部集合约束的情况,也易于处理智能体不同局部集合约束的情形.不同于现有渐进收敛算法[3-16],本文的算法能在固定时间内收敛于最优解.采用固定时间李雅普诺夫函数法严格证明了算法的固定时间收敛特性.在满足全局目标函数强凸的条件下,本算法允许局部目标函数是非凸的.
1 问题描述和预备知识

1.1 问题描述
考虑由n个智能体组成的多智能体系统,每个智能体的动力学模型由如下的连续时间单积分器描述

其中,xxxi ∈Rm表示第i个智能体的状态,uuui ∈Rm为第i个智能体的控制输入.本文将设计控制输入uuui使得多智能体系统在固定时间内求解如下带集合约束的优化问题
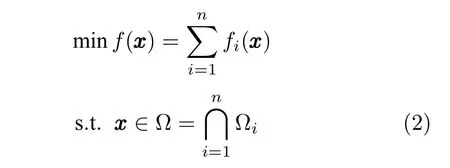
其中,全局目标函数f(xxx)为每个智能体的局部目标函数fi(xxx):Rm →R 之和;Ωi ⊂Rm为闭凸集合,表示第i个智能体的局部集合约束;fi(xxx) 和 Ωi为第i个智能体的局部信息.优化问题(2)等价于如下优化问题
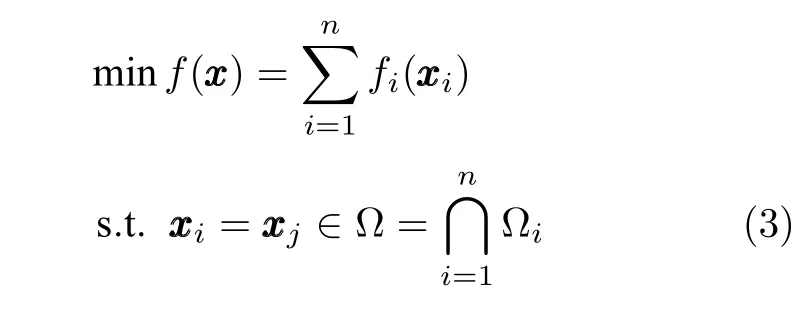
优化问题(2) 和(3) 有广阔的工程应用范围.例如,智能电网中储能系统的优化管理和电力负载的最优分配[12,30,32],传感器网络中未知参数的估计和未知目标的定位[32-33],机器学习中基于损失函数最小化的模型拟合[1].


为实现多智能体系统(1)在固定时间内求解优化问题(3),本文给出如下假设.
假设 1.局部目标函数fi(xxx)是连续可微的,全局目标函数f(xxx)是强凸的.
假设 2.所有局部闭凸集合 Ωi的交集是非空的,即 ΩØ.
注 1.假设1 和假设2 意味着优化问题(2)有唯一最优解[35].全局目标函数的强凸性不要求所有局部目标函数是强凸的(或者凸),这意味着本文的假设允许某些局部目标函数是非凸的,仿真实例将进一步说明.
1.2 代数图论

1.3 相关引理

下面的引理推广文献[29]中引理1,使得本文的控制参数不依赖拉普拉斯矩阵的最小非零特征值.


2 分布式固定时间优化控制算法
在本节,首先解决智能体相同局部集合约束下的优化问题(2),即 Ωi=Ωj=Ω 时的情形;然后考虑局部约束集合不同的情形.
2.1 相同局部集合约束下的分布式优化

其中,k1,k2,c1,c2为正的增益,T2,T3为设定的时间参数.由引理5 和后续的分析过程可知,时变增益的时间参数T直接影响控制器的收敛时间.理论上,时间参数T2,T3可以设置为任意正常数以满足任务需求;而实际应用中,时间参数会受物理设备的约束.因此,该参数可在物理允许的范围内根据期望的收敛时间值直接设置.
引理 6.当假设1 和假设2 成立,在控制协议(15)的作用下,每个智能体的状态量在固定时间内收敛到约束集合,即存在一个固定时间T1,当t ≥T1时,xxxi=PΩ(xxxi),∀i.
证明.选择如下李雅普诺夫函数

对式(21)右侧第1 项应用引理2,可得

引理 7.如果多智能体系统的无向通信拓扑是连通的,且假设1 和假设2 成立,多智能体系统(1)在控制协议(15)作用下,且增益k3≥2n时,所有智能体的状态量在固定时间T1+T2内实现一致.
证明.由引理6 可知,当t≥T1时,有xxxi=PΩ(xxxi).因此当t≥T1时,智能体的动态特性可描述为


对式(28)右侧的第ItemⅠ项,考虑到通信图G是无向且连通的,可得



应用引理5 可知,V3在固定时间T3内收敛到0,即当t≥T1+T2+T3时,有xxxi=xxx*(∀i),这表明智能体的状态量在固定时间内收敛到最优解.因此控制协议(15)作用下的多智能体系统(1)在固定时间内求解相同局部集合约束下的优化问题(2).□
2.2 不同局部集合约束下的分布式优化
本小节进一步推广控制协议(15)以处理不同局部集合约束下的优化问题(2).此时,控制协议uuui设计为
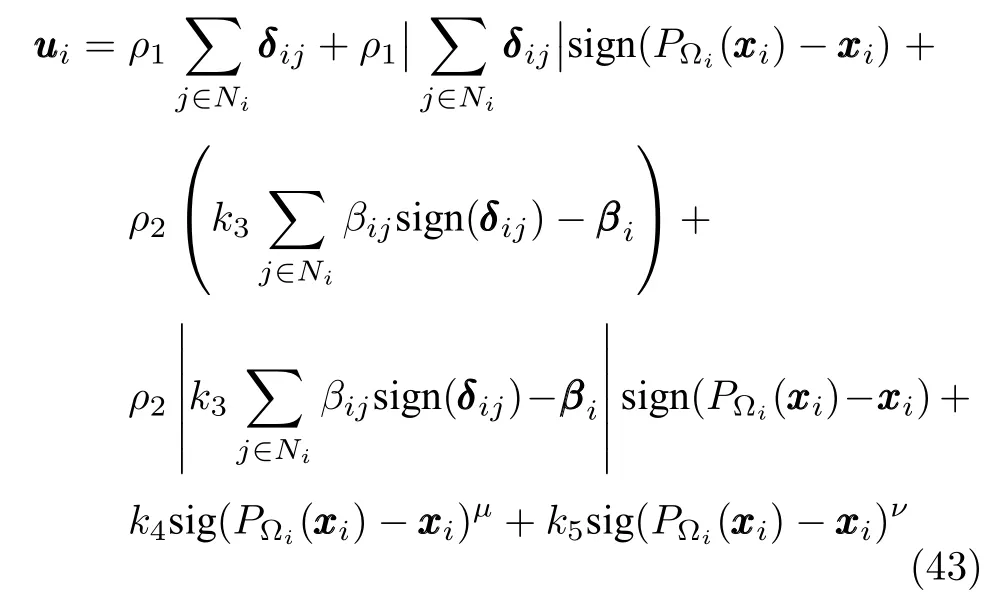
其中,各个参数的定义与式(15)一致.不同于协议(15)只能解决所有智能体具有相同局部集合约束下的优化问题,协议(43)通过等式右侧第2 项来处理不同局部约束投影的影响,使得协议(43)能解决不同智能体具有不同局部集合约束下的优化问题.因此协议(43)解决的问题比协议(15)更广泛.而从另一方面看,由于协议(15)比协议(43)少一项,在解决相同局部集合约束下的优化问题(2)时,协议(15)有相对少的计算量.
引理 8.当假设1 和假设2 成立,在控制协议(43)作用下,每个智能体状态量在固定时间内收敛到约束集合,即存在一个固定时间T1,当t≥T1时,∀i,xxxi=PΩi(xxxi).
证明.选取如下李雅普诺夫函数


定理 2.如果多智能体系统的无向通信拓扑是连通的,且假设1 和假设2 成立,多智能体系统(1)在控制协议(43)作用下,且增益k3≥2n时,智能体的状态量在固定时间内收敛于不同局部集合约束下优化问题(2)的解.
证明.由引理8 可知,当t≥T1时,智能体的动态特性可描述为
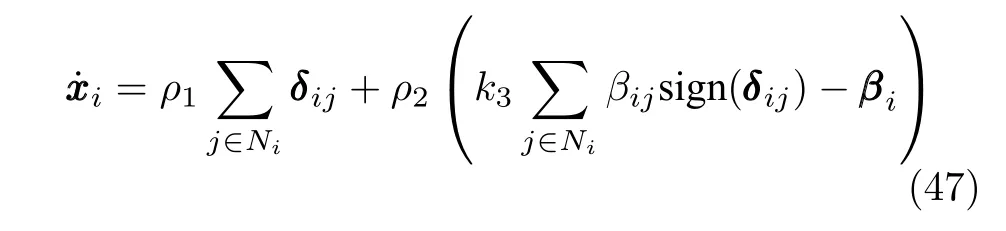
对式(47)应用引理7 可知,智能体的状态在固定时间T1+T2内实现一致,即xxxi=∈Ω.因此当t ≥T1+T2,智能体的动力学特性为
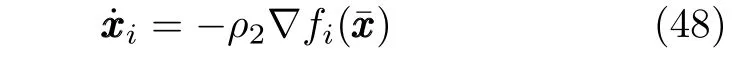
最后,采用与定理1 相同的分析可得,在固定时间T1+T2+T3后,所有智能体的状态满足xxxi=xxx*.因此控制协议(43)下的多智能体系统(1)在固定时间求解不同局部集合约束下的优化问题(2).□
注 2.文献[29]固定时间一致性协议的增益参数依赖于拉普拉斯矩阵的最小非零特征值;而本文的控制协议放宽了该条件.基于改进的引理5,控制协议(15)和(43)的控制增益参数k3只与智能体的个数有关.如果智能体个数是未知的,可以利用固定时间一致性协议来估计.例如,每个智能体赋予一个辅助变量,令一个智能体的辅助变量初值为1且其余智能体的辅助变量初值为0,应用固定时间平均一致性协议,可得到平均值 1/n,从而获得智能体的个数.因此,本文提出的算法能以全分布式的方式实现.
注 3.注意到本文证明过程中所选择的李雅普诺夫函数V1,V2,V3,V4均不依赖通信拓扑.因此,这些函数能作为公共李雅普诺夫函数来分析固定时间优化算法在时变拓扑下的稳定性.
注 4.本文研究的分布式固定时间优化问题假设通信拓扑是无向连通的,该假设在现有分布式优化问题的研究中是普遍的,如文献[7-20,30-31]也使用相同的假设.我们未来将进一步考虑更一般的通信拓扑情况,如文献[3-5]考虑的联合连通图、文献[6]考虑的强连通有向图.

3 数值仿真


首先进行相同局部集合约束下的优化仿真研究.仿真中,所有智能体的局部集合约束均设置为Ω={xxx ∈R2|5≤x1≤13,5≤x2≤13}.为说明分布式算法的正确性,通过MATLAB 的fmincon 函数求得最优解为 [x1,x2]≈[5.00,5.00].根据定理1,对任意初始状态,控制协议(15)在固定时间1.9 s内求解优化问题.由图1 的仿真结果可见,所提出的分布式协议(15)在1.9 s 内使得所有智能体的状态到达集合约束内的最优点,即在固定时间内求解优化问题.
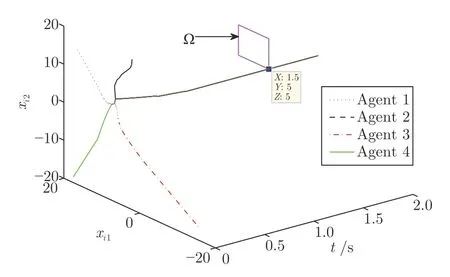
图1 相同局部集合约束下优化问题(2)的仿真结果Fig.1 Simulation results for optimization problem (2) with a common constraint set
接下来,进行智能体局部集合约束不同情形下的优化仿真研究.4 个智能体的局部集合约束分别设置为 Ω1={xxx ∈R2|0≤x1≤10,0≤x2≤8},Ω2={xxx ∈R2|-4≤x1≤12,1≤x2≤10},Ω3={xxx ∈R2|2≤x1≤14,-4≤x2≤12},Ω4={xxx ∈R2|4≤x1≤16,3≤x2≤14}.通过fmincon 函数求得最优解为[x1,x2]≈[4.00,4.29].图2 给出控制协议(43)下智能体的状态轨迹.由图可知,所有智能体的状态在1.9 s 内收敛到公共约束集合内的最优点.
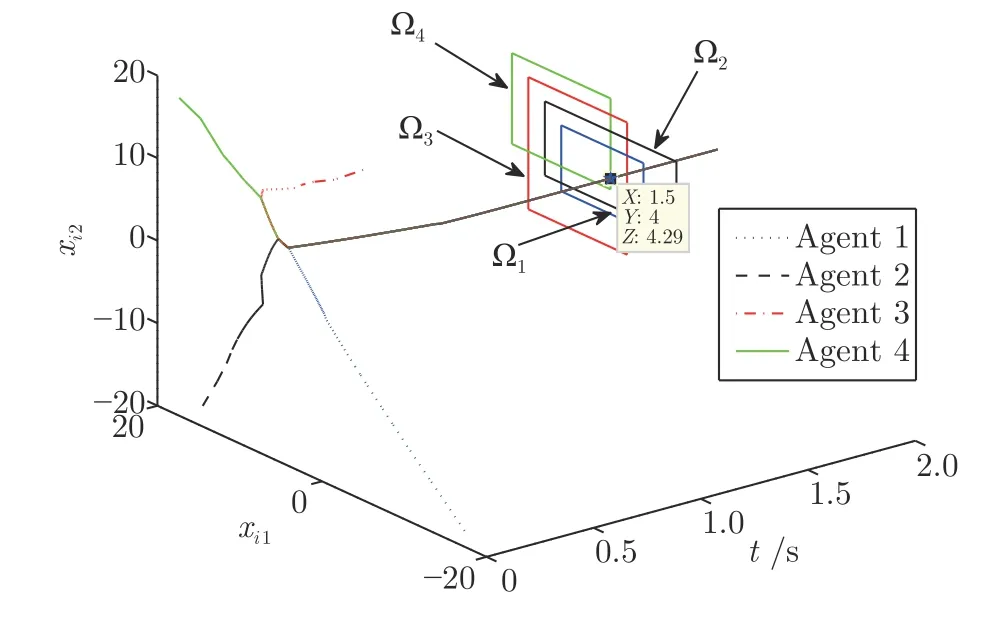
图2 不同局部集合约束下优化问题(2)的仿真结果Fig.2 Simulation results for optimization problem (2)with nonidentical local constraint sets
为展示本文提出的优化控制算法的优越性,下面进行本文算法与文献[17,30]算法的比较研究.为方便,文献[17]提出的分布式有限时间零梯度和优化算法与文献[30]提出的基于固定时间一致性的分布式优化算法分别写为
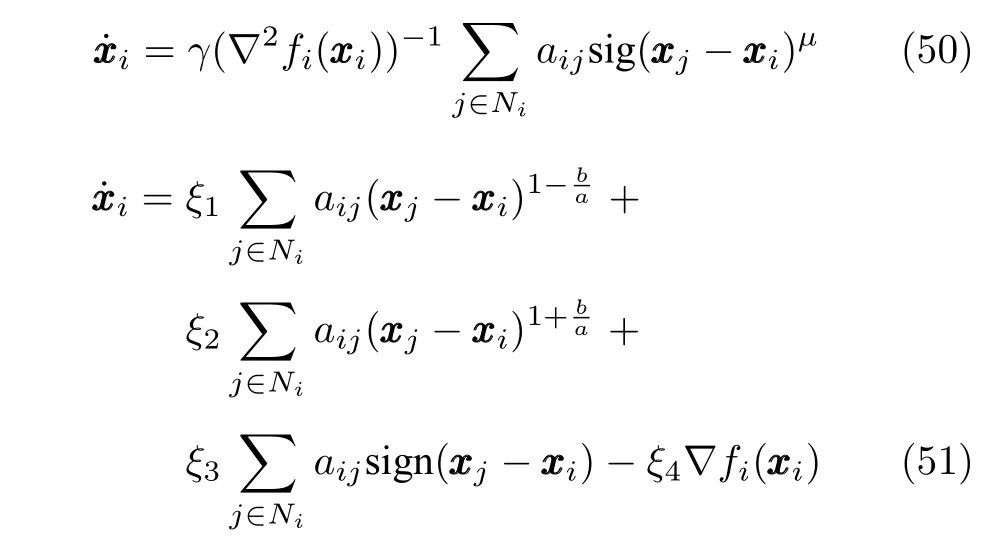
正如引言中所述,传统有限时间一致性算法(如文献[21-23,25-29])通常无法直接解决优化问题.从式(50)和式(51)可知,文献[17]的算法是一种基于时变权重的有限时间加权一致性优化算法,文献[30]的算法是一种结合固定时间一致性和梯度法的渐近优化算法.在这个仿真中,采用前一个案例研究的通信拓扑,算法的增益参数设置为相同值,每个智能体的成本函数为
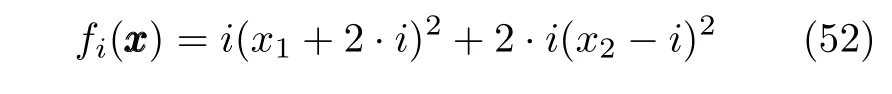
图3 展示了几种算法在不同初始条件下状态误差范数‖XXX -XXX*‖2随时间的变化过程,其中由图3 可知,本文提出的分布式优化算法在设计的固定时间内从任意初始点收敛到最优点;文献[17]的分布式优化算法在有限时间内收敛到最优点,但收敛时间随初值的增长而增长;文献[30]的分布式优化算法渐近的收敛到最优点.因此,固定时间优化比渐近时间优化和有限时间优化有优势.此外应注意两点:一是文献[17]和文献[30]的算法仅解决无约束优化问题,而本文提出的算法解决带集合约束的优化问题;二是文献[17]的算法需要每个局部目标函数是二次连续可微的强凸函数,文献[30]的算法需要每个局部目标函数是类二次型的,而本文提出的算法仅需要连续可微的全局目标函数是强凸的,允许局部目标函数是非凸的.
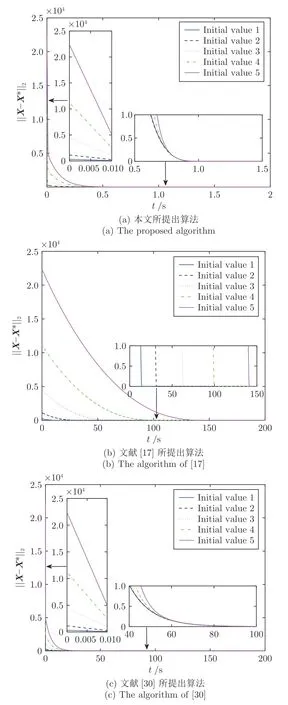
图3 几种算法在不同初始条件下状态误差范数‖XXX -XXX*‖2 随时间的变化Fig.3 The state errors norm of several algorithms‖XXX -XXX*‖2 with time for various initial conditions
4 结束语
本文研究带集合约束优化问题的分布式快速求解算法.首先,对于智能体相同局部集合约束下的优化问题,基于固定时间投影和时变增益技术,提出一个分布式固定时间优化算法.接着,该算法推广到智能体不同局部集合约束情形.所提出的分布式算法使得多智能体系统在固定时间内解决带集合约束的优化问题,算法的收敛时间能根据任务需求来预先设计.在后续研究中,我们将进一步考虑有向通信拓扑和高阶动态系统下的分布式固定时间优化问题.

