扰动振幅和扰动频率对Fermi-Pasta-Ulam-Tsingou 回归现象的影响

郑州 李金花 马佑桥 任海东

1) (南京信息工程大学物理与光电工程学院,南京 210044)

2) (江苏海威光电科技有限公司,南通 226000)

Fermi-Pasta-Ulam-Tsingou (FPUT)回归现象指一个多模非线性系统能周期性回到初始激发态的一个复杂的非线性过程,与该非线性系统的调制不稳定性密切相关.针对实验中能如何较为方便地观察到FPUT 回归现象以及能如何观察到更多FPUT 循环的问题,本文基于调制不稳定性重点分析研究了施加在平面波上的扰动振幅和扰动频率对所观察到的FPUT 循环的影响.我们发现,扰动振幅可以极大程度地影响所观察到的FPUT 现象: 1) FPUT 循环数对扰动振幅的值非常敏感,扰动振幅越大,FPUT 循环数越多;2) 扰动振幅较小(较大)时,相应的FPUT 循环频谱就比较规则(很不规则).相比之下,扰动频率对FPUT 循环数的影响不是很大(在最佳调制频率附近的一个小范围内,可观察到FPUT 循环最多),但是它对脉冲周期性振幅最大位置处所激发的高阶频率成分的影响比较大,扰动频率越大(越小),其可以激发的高阶频率成分越少(越多).本文的研究结果将对FPUT 实验的观测和理论发展提供一定的帮助.

1 引言

Fermi-Pasta-Ulam-Tsingou (FPUT)回归现象指一个多模系统周期性回归到初始激发态的非线性过程[1],是物理学领域中经典的非线性问题,由Fermi 等[1]在1955 年使用第一代计算机仿真模拟多粒子非线性振动时发现.FPUT 的发现是非线性物理学发展史上一个重要的里程碑,该研究直接促使了1965 年“孤子”概念的提出,是近代理论物理和可积系统研究的起点[2].随着仪器精度和制作工艺的进步,近年来FPUT 回归现象陆续在热传输动力学[3]、晶格动力学[4]、流体力学[5]以及非线性光学[6]等不同物理领域的实验中被观察到.

调制不稳定性是加在平面波上的微小扰动随传输距离(或传输时间)指数增长的一种不稳定性行为.由于能量不会无限增长,所以加在平面波上的微小正弦扰动在实际的模拟和实验中均不会随传输距离无限地指数增长,而是当其增加到一定程度后快速衰减,形成一系列的周期性脉冲,该过程随着传输距离(或传输时间)的增加会周期性地复现,这一演化过程即FPUT 回归现象[7-9].理论上讲,FPUT 回归现象与该非线性系统的严格双周期波解[10-16]、Akhmediev 呼吸子解[17]及其他新型局域波解[18,19]等密切相关.尽管如此,人们发现FPUT回归现象的主要特征可以通过分析平面波的调制不稳定性来定量地获取[10-16],国际上发现了最新且非常有趣的研究结果,如由扰动平面波的非线性演化描述一定高阶效应下非线性系统的解析非对称FPUT 回归频谱[20],以及不同扰动频率会带来结果相变[21]等.

自2001 年在光学实验中首次观察到FPUT现象以来[6],FPUT 的研究再次成为了非线性物理领域的一个研究热点[7-9,22-30].理论方面,人们构建了形成FPUT 不同种类的呼吸子解及双周期波解[7-9]、预测了首次FPUT 及第二次FPUT 出现的位置[23,24]、研究了高阶谐波的形成过程[25-27,31]、泵浦和扰动信号的初始相位差以及线性损耗和高阶色散对FPUT 回归现象的影响[28-30]等.实验方面,人们设计了不同的实验方案观测FPUT 回归现象,且改进实验方案尝试在实验中能观察到更多的FPUT 循环[30,32-37].

文献[30,32-37]所报道的实验基本上都是给定一组特定的扰动参数来观察FPUT 回归现象,同时从理论上一定程度地讨论了各项扰动参数对FPUT 回归现象的影响[30,32-37].针对如何在光学实验中能相对容易地观察到FPUT 回归现象,以及如何能观察到更多FPUT 循环的问题,本文基于调制不稳定性分析通过数值模拟方法较为系统地研究了扰动振幅和扰动频率对FPUT 回归现象的影响.本文研究结果将为FPUT 的实验观察提供一定的理论支持.

2 模型方程与调制不稳定性增益谱

本文主要考虑非线性光纤光学领域的经典模型方程,忽略光纤的损耗,平面波在单模光纤中传播的非线性控制方程为

其中,A为单模光纤中电场的慢变包络,z是传播距离,t是时间坐标,β2是群速度色散系数,三阶克尔非线性系数γ=2πn2/(λAeff)(n2是折射率,λ是载波波长,Aeff是有效模面积).方程(1)的平面波解为

其中,P0是z=0 处的入射功率,γP0z是克尔效应引起的非线性相移.平面波(2)式在光纤的正常色散区域(β2＞0)比较稳定,施加在平面波上的微小扰动不会随传输距离的增加而增长,而在光纤的反常色散区域(β2＜0),平面波是不稳定的,加在平面波上的微小扰动会随着传输距离的增长而急剧增长.依据线性稳定性分析方法,其对应的调制不稳定性增益谱为[38]

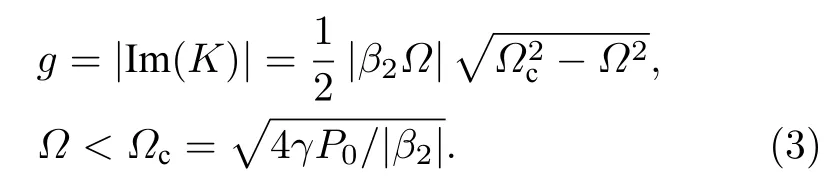
峰值增益及最佳扰动频率(即能产生峰值增益的扰动频率)分别为

在(3)式和(4)式中,K和Ω分别代表扰动波束和扰动频率.

3 FPUT 回归现象

调制不稳定性与FPUT 回归现象密切相关,本文基于调制不稳定性研究扰动振幅和扰动频率对FPUT 回归现象的影响,采用实验中常见的一类初始条件[30,32-36],即

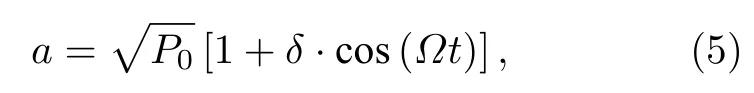
其中δ为扰动振幅,Ω为满足(3)式的扰动频率.

人们在研究FPUT 问题时,通常都是在某一给定扰动振幅和扰动频率条件下进行,而忽略了不同扰动振幅和不同扰动频率对所观察到的FPUT现象的影响.本文发现扰动振幅和扰动频率均可以对所观察到的FPUT 现象产生极大的影响,研究中采用常见的单芯单模非线性光纤参数即β2=—0.02 ps2/m,γ=2.5 kW—1·m—1.这里我们需要声明本文以下结果的讨论适用于其他在实验中常见的入射条件[30,32-36].

3.1 扰动振幅的影响

在本节研究中,不失一般性地固定扰动频率为能产生增大增益的最佳扰动频率,即Ω=Ωmax=.图1(a)和图1(b)分别描述平面波随传输距离的三维波形演化和频谱演化(δ=0.001,P0=1 kW,Ω=Ωmax=rad/ps);图1(c)和图1(d)给出了脉冲振幅在首次增长到峰值的空间距离处(z1FPUT=3.2 m)的波形和频谱.如图1(a)所示,脉冲振幅增加至最大值后快速衰减至初始状态,即FPUT 回归现象.从图1(a)和图1(b)中可观察到3 个完整的FPUT 循环,z1FPUT=3.2 m 与文献[23,24]中所预测的z1FPUT==3.04 m 符合地非常好,相邻两次脉冲振幅增长至最大值的空间位置呈等间距分布.图1 所反映的FPUT 回归现象的主要特征与文献[23,24]在同样初始条件下的结果类似.当传输距离约大于20 m时,FPUT 现象消失,非线性波的演化开始变得毫无规律,这应该是由非线性所激发的多频率成分之间的相互作用所导致,此外可能和数值模拟所引入的噪声有一定的关系(在实际实验中,噪声总是存在,我们的模拟结果是合理的).

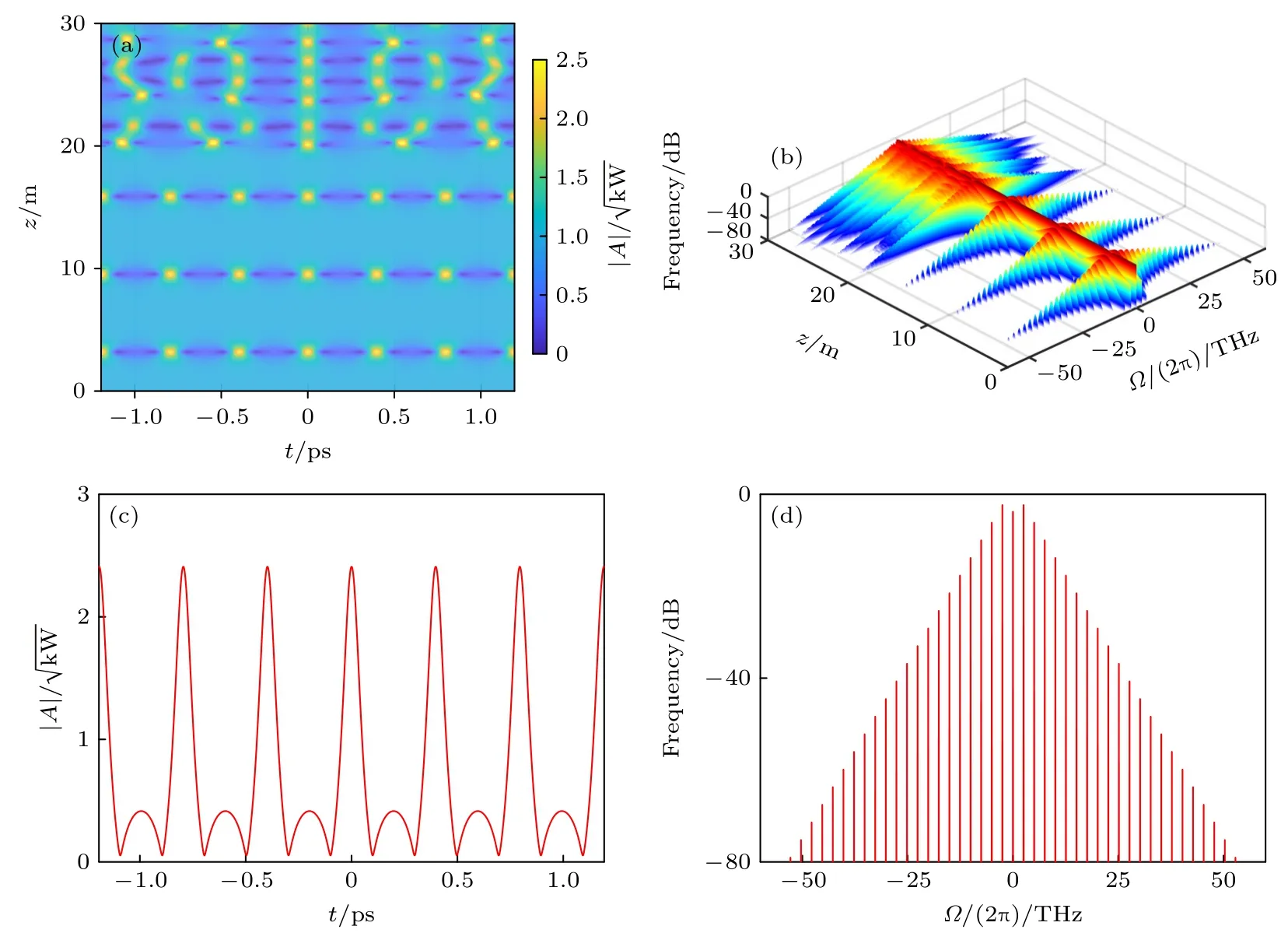
图1 非线性光纤中,扰动平面波(a)和相应频谱(b)随传输距离的演化;平面波演化至z1FPUT=3.2 m 处的波形(c)及频谱(d).图中P0=1 kW,δ=0.001,Ω=Ωmax=rad/psFig.1.Evolution of perturbed plane wave (a) and corresponding spectra (b) with transmission distance;wave form (c) and corresponding spectra (d) at z1FPUT=3.2 m in typical single-core fibers for P0=1 kW,δ=0.001,Ω=Ωmax=rad/ps .

当扰动振幅增长时 (δ=0.1,其他参数不变),平面波的演化如图2 所示.与图1 相比,平面波的演化过程主要有三方面显著的变化.第一,FPUT循环数明显增长,这是图2 (11 个FPUT 循环)区别于图1 (3 个FPUT 循环)最大的不同之处;第二,同一个时刻处,脉冲振幅相邻两次出现最大值的空间周期减小 (图1 周期为z1,2=6.3 m,图2周期为z1,2=2.7 m);第三,如理论预测,z1FPUT随δ的增加而逐步减小.从物理角度来看,上述变化可以解释为: 固定泵浦功率P0和扰动频率Ω(见(5)式),扰动功率增长的速度将随扰动振幅δ的增加而增加,因此,脉冲振幅首次增长至峰值所需要的传输距离z1FPUT就变短,两相邻脉冲振幅最大值的空间周期随之而变小;同时由于完成一个FPUT 循环的空间周期快速缩短,非线性所激发的多个频率成分还没有来得及相互作用就又开始下一个循环,相应地,FPUT 循环数也随δ的增加而快速增加.

图2 非线性光纤中,扰动平面波(a)和相应频谱(b)随传输距离的演化;平面波演化至z1FPUT=1.3 m 处的波形(c)及频谱(d).图中P0=1 kW,δ=0.1,Ω=Ωmax=rad/psFig.2.Evolution of perturbed plane wave (a) and corresponding spectra (b) with transmission distance;wave form (c) and corresponding spectra (d) at z1FPUT=1.3 m in typical single-core fibers for P0=1 kW,δ=0.1,Ω=Ωmax= rad/ps .

当扰动振幅进一步增加 (δ＞0.1,其他参数保持不变),如图3 所示,FPUT 循环数随δ增加而继续大幅增加,z1FPUT随δ的增加而持续减小,两相邻FPUT 形成的空间间距进一步缩小.同时我们注意到,当δ比较大时,平面波的波形演化和频谱演化变得越来越不规则,如图4 所示 (δ=0.7).当δ较大时,调制信号就变得比较强,原来由线性理论所计算的调制不稳定性就不再完全适用,这时调制信号的非线性就会比较突出,因此我们认为频谱和波形演化得不规则性应该是由调制信号和泵浦信号之间的强相互作用所引起.

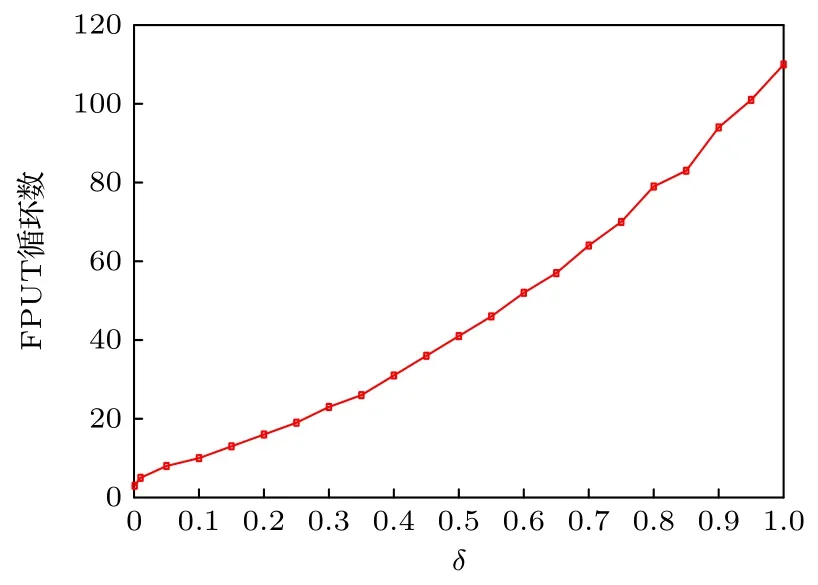
图3 非线性光纤中FPUT 循环数随扰动振幅δ 的演化Fig.3.Variation of the number of FPUT cycle with the perturbation amplitude δ in nonlinear fibers.

图4 非线性光纤中,扰动平面波(a)和相应频谱(b)随传输距离的演化;平面波演化至z1FPUT=0.4 m 处的波形(c)及频谱(d).图中P0=1 kW,δ=0.7,Ω=Ωmax= rad/psFig.4.Evolution of perturbed plane wave (a) and corresponding spectra (b) with transmission distance;wave form (c) and corresponding spectra (d) at z1FPUT=0.4 m in typical single-core fibers for P0=1 kW,δ=0.7,Ω=Ωmax= rad/ps.

通过本节分析,发现实验可观察的FPUT 循环数随扰动振幅的增长而急剧增长,而且当扰动振幅较大时,平面波的波形演化和频谱演化变得越来越不规则.该发现尚未在文献中有过报道.

3.2 扰动频率的影响

当扰动频率满足Ω＜Ωc/2 时,高阶谐波成分将会被激发[25-27],本节考虑不激发高阶谐波情况下,即当扰动频率满足Ωc≥Ω≥Ωc/2 时,扰动频率对所观察到的FPUT 现象的影响.

图5(a)和图5(b)分别反映了扰动平面波随传输距离的波形演化和频谱演化(P0=1 kW,δ=0.001,Ω=Ωc/2=rad/ps);图5(c)和图5(d)分别为脉冲振幅在z1FPUT=3.4 m 处的波形和频谱.可以看出Ω=Ωc/2 时有两个完整的FPUT 循环(图5(a)和图5(b)),且当z=z1FPUT时,在[—80 dB,0 dB]的相对出射光强范围内可观察到64 个非线性所激发的高阶谐波(图5(d)).

通过大量的数值模拟计算发现,当扰动频率从Ω=Ωc/2 开始增加时,在相同的相对出射光强范围内,可观察到的高阶谐波数呈明显的递减趋势,如图6 所示.随着Ω的增加,可观察到的高阶谐波数显著递减的原因和z1FPUT处脉冲所具备的光强密切相关.Ω越大,z1FPUT处脉冲的振幅越小,光强越弱,非线性效应就越弱,相应地,非线性所激发的高阶谐波成分就越少.对比图5(c)和图1(c),扰动频率为Ω=Ωc/2 的扰动平面波在z1FPUT处演化出的脉冲最大振幅|a|max=2.688,明显大于扰动频率为Ω=Ωmax情况下扰动平面波在z1FPUT处演化出的脉冲最大振幅|a|max=2.403,这应该和高阶谐波成分与入射扰动频率成分在传输中产生的复杂非线性相互作用有关.

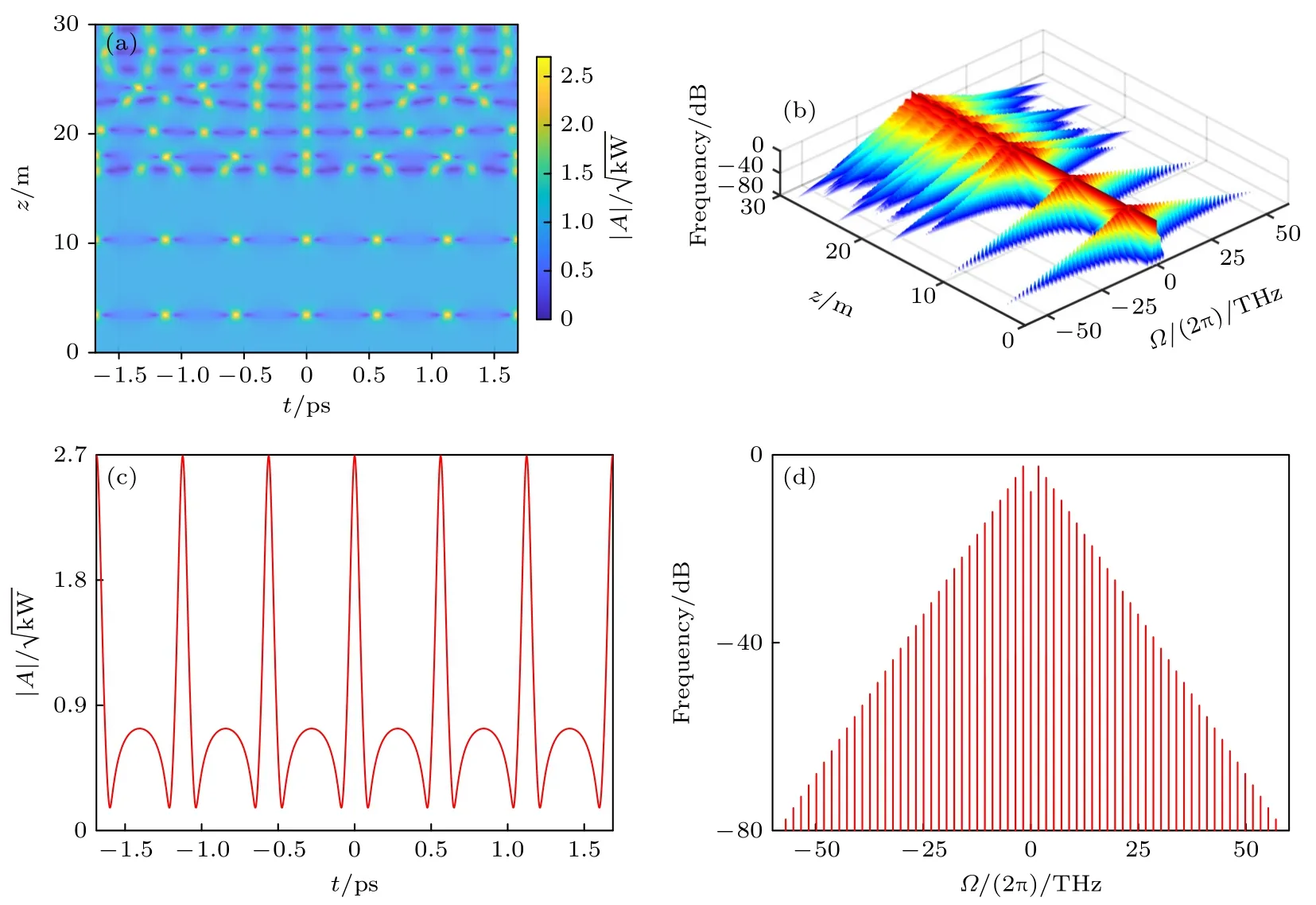
图5 非线性光纤中,扰动平面波(a)和相应频谱(b)随传输距离的演化;平面波演化至z1FPUT=3.4 m 处的波形(c)及频谱(d).图中P0=1 kW,δ=0.001,Ω=Ωc/2=rad/psFig.5.Evolution of perturbed plane wave (a) and corresponding spectra (b) with transmission distance;wave form (c) and corresponding spectra (d) at z1FPUT=3.4 m in typical single-core fibers for P0=1 kW,δ=0.001,Ω=Ωc/2=rad/ps .

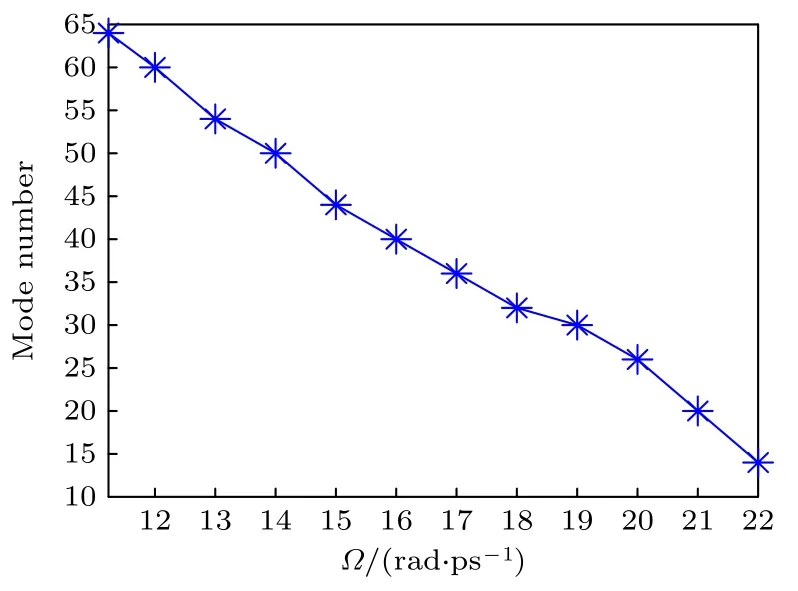
图6 高阶谐波数随扰动频率Ω (Ωc/2＜Ω＜Ωc)的变化关系图Fig.6.Variation of mode numbers of high-order sidebands with perturbation frequency Ω (Ωc/2＜Ω＜Ωc).

随着扰动频率从Ω=Ωc/2 开始增加,如图5(d)所示,FPUT 循环周期数先缓慢增长,在Ω=Ωmax附近处,FPUT 循环周期数最多(见图1).当Ω＞Ωmax时,FPUT 循环周期又开始缓慢减少(见图7,Ω=22 THz).在Ω=Ωmax附近处出现最多的FPUT 循环数在物理层面上是可以理解的.最佳扰动频率对应的增益最大,以该频率作为扰动信号频率,扰动增长的速度最快,所以FPUT 出现的速度就会非常快,导致出现的FPUT 周期数相应地比较多.相反,当扰动频率Ω≠Ωmax＜Ωc时,平面波演化过程中所出现的噪声中,Ωmax成分振幅会随着传输距离增加而迅速增强,从而导致Ωmax频率成分和入射的Ω频率成分产生强相互作用而破坏掉原来的FPUT,所以Ω≠Ωmax＜Ωc时所观察到的FPUT 循环数比较少.

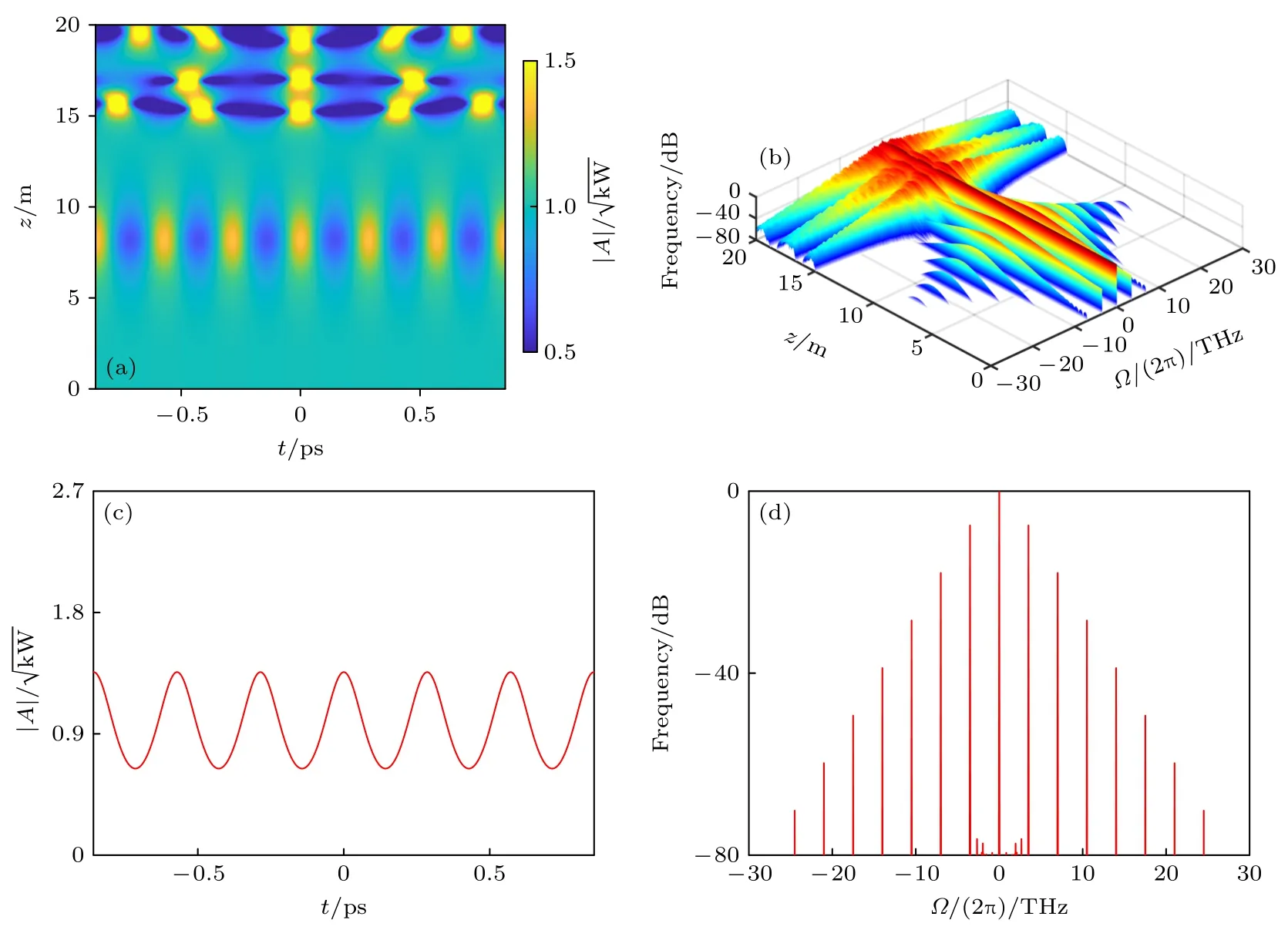
图7 非线性光纤中,扰动平面波(a)和相应频谱(b)随传输距离的演化;平面波演化至z1FPUT=8.22 m 处的波形(c)及频谱(d).图中P0=1 kW,δ=0.001,Ω=22 rad/psFig.7.Evolution of perturbed plane wave (a) and corresponding spectra (b) with transmission distance;wave form (c) and corresponding spectra (d) at z1FPUT=8.22 m in typical single-core fibers for P0=1 kW,δ=0.001,Ω=22 rad/ps.

当扰动频率增至Ω=Ωc=22.3607 rad/ps 时,平面波稳定,FPUT 消失,如图8(d)所示.当扰动频率Ω=Ωc时,调制不稳定性消失,入射的扰动频率不会随传输距离的增加而增长,随着传输距离的增加,在光纤某距离处由噪声引入的最佳调制频率成分出现并迅速增长,同时会与其他调制频率成分在传输中产生相互作用,最终导致频谱的极端不规则性,在整个过程中观测不到FPUT 现象.

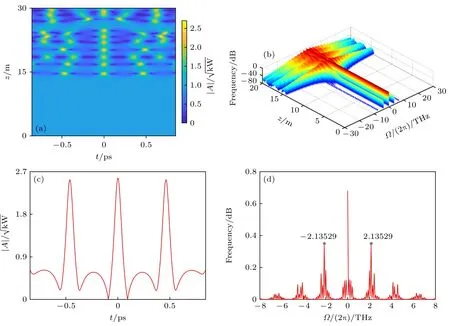
图8 非线性光纤中,扰动平面波(a)和相应频谱(b)随传输距离的演化;平面波演化至z1FPUT=14.6 m 处的波形(c)及频谱(d).图中P0=1 kW,δ=0.001,Ω=22.3607 rad/psFig.8.Evolution of perturbed plane wave (a) and corresponding spectra (b) with transmission distance;wave form (c) and corresponding spectra (d) at z1FPUT=14.6 m in typical single-core fibers for P0=1 kW,δ=0.001,Ω=22.3607 rad/ps.

4 结论

基于调制不稳定性分析,本文通过数值模拟系统地研究了扰动振幅和扰动频率对单模单芯光纤中FPUT 现象的影响,发现扰动振幅和扰动频率可以极大程度地影响所观察到的FPUT 现象.扰动振幅对所观察到的FPUT 循环数的影响极大.扰动振幅越大,可观察到的FPUT 循环数越多,当扰动振幅较小时,相应的FPUT 频谱演化就比较规则,相反,相应的FPUT 频谱演化就非常不规则.扰动频率对所观察的FPUT 循环数的影响不大,但是它可以极大地影响在脉冲振幅最大位置处所产生的高阶谐波成分的数目.扰动频率越大,所产生的高阶谐波成分就越少.

为了方便FPUT 的实验观测能观察到更多的FPUT 循环,分析发现实验中扰动振幅要设置得较大,同时扰动频率应该选择在最佳扰动频率附近的值域.同时应强调,大的扰动振幅对应的FPUT 谱会比较不规则,当扰动频率比较大时,其所激发的高阶谐波成分就会非常少.相信本文的研究结果将对基于调制不稳定性分析的FPUT 实验观测以及理论理解提供一定的帮助.非线性光纤中有待解决的FPUT 问题还有很多,包括非传统调制不稳定性相关的FPUT 研究[7,8]、高阶效应对实验观察到的FPUT 的影响[39]等,这将是我们下一步研究的主要任务.