针梳机罗拉导柱径向圆跳动的视觉测量方法
韩京海,金守峰,沈文军,肖福礼,严 楠
(1.南京交通职业技术学院 轨道交通学院,江苏 南京 211188; 2.西安工程大学 机电工程学院,陕西 西安 710600;3.陕西省计量科学研究院,陕西 西安 710100; 4.宁波职业技术学院 机电工程学院,浙江 宁波 315800)
针梳机广泛应用于精梳毛纺、化学纤维等前纺工艺过程,通过罗拉牵伸可有效改善纤维的松解平直状态及毛条结构的均匀程度,适宜精梳长纤维。牵伸罗拉作为纺织机械针梳机的重要零部件,其几何精度会影响纤维牵伸质量。目前针梳机牵伸罗拉的几何精度检测主要以人工接触式测量为主,测量仪器的测头与牵伸罗拉导柱表面的直接接触从而产生接触摩擦,不仅容易划伤被测物表面,也影响了测量的精度。

1—罗拉工作面;2—罗拉导柱;3—罗拉颈。图1 牵伸罗拉及圆跳动公差Fig.1 Draft roller and circular runout tolerance. (a)Physical map; (b)Circular runout tolerance marking; (c)Tolerance zone
随着机器视觉测量技术的发展,通过视觉测量技术代替人工进行几何精度的测量在各领域得到了应用。彭凯等[1]提出一种用于适用于低转速机床主轴径向跳动误差的机器视觉测量系统,利用CCD传感器获得主轴跳动图像,测量精度达到了的径向跳动误差亚微米级。郭学庆等[2]设计优化算法有效分离主轴回转误差,并采用最小二乘法评定了主轴回转精度。周晓东等[3]提出了一种基于线结构光的圆柱度测量方法,根据轴类零件的特征,建立了结构光测量模型,其测量精度为20 μm,为圆柱度的评价提供可靠数据。胡凌皓等[4]提出了一种基于计算机视觉技术的罗拉倒角非接触测量方法,通过提取罗拉轮廓影像的根底部倒角特征参数,实现对不同尺寸的回转类工件的倒角自动检测。郭天太等[5]提出了二维投影式轴类零件测量方法,实现了对花键齿顶圆、长轴等半径及长度的非接触式测量,准确率达99.8%。贺秋伟等[6]针对滚珠螺母的形位公差测量要求,提出了基于计算机视觉的检测方法,通过图像处理提取螺母的单像素边缘点,以螺母的圆度、圆柱度及跳动等视觉测量模型实现滚珠螺母几何公差的测量。张学昌等[7]提出了在图像域中基于误差转换的曲轴圆度及圆柱度误差评价方法,通过建立圆度、圆柱度评价模型对曲轴轴颈形状误差进行测量。刘勇等[8]提出了基于工业CT图像的管道内表面圆柱度测量方法,以Facet模型提取管道内表面CT图像的边缘点信息,建立最小二乘圆柱圆柱度测量模型测量管道内表面的圆柱度。庞云龙等[9]对光纤端面图像进行预处理,提取边缘轮廓特征,建立基于最小二乘椭圆拟合的纤芯和包层端面圆度评价模型,通过MatLab软件实现了光纤端面不圆度的测量。周金波等[10]对冲孔的圆度测量提出一种图像形态学融合最小二乘法拟圆的边缘拟合方法,替代图像拼接方法,实现了对冲孔圆度、半径及位置的测量。陈厚瑞等[11]利用显微视觉技术获取微球图像,基于微球边缘轮廓建立基于最小二乘圆拟合算法的微球圆度测量模型,实现对微球圆度有效检测。杨建西等[12]采用机器视觉方法对机油泵内外转子结构参数进行非接触式测量,以改进最小二乘法提取机油泵亚像素边缘信息,建立机油泵内外转子结构参数模型,实现中心距、圆度等几何量的中高精度测量。金守峰等[13]提出了一种基于回转类零件横截面轮廓的圆度视觉测量方法,以改进Zernike矩算法提取零件横截面轮廓的亚像素边缘信息,通过建立圆度模型测量回转类零件的直径与圆度。综上所述,对于针梳机罗拉导柱径向圆跳动主要依靠人工检测。
基于此,本文提出基于机器视觉的牵伸罗拉导柱圆跳动测量方法,通过背光成像获取旋转过程中的罗拉导柱轴截面序列图像,采用三次多项式拟合算法提取罗拉导柱轴截面边缘亚像素轮廓特征,以最小二乘法拟合基准轴线,构建图像域下的圆跳动测量模型,实现针梳机牵伸罗拉导柱圆跳动的非接触式测量。
1 基于机器视觉的牵伸罗拉导柱径向圆跳动测量系统
1.1 牵伸罗拉
图1(a)所示为针梳机牵伸罗拉,由罗拉颈、罗拉工作面及罗拉导柱等表面构成,罗拉颈安装在罗拉座上,工作面加工有沟槽,以对牵伸罗拉的工作面构成钳口夹持纱条,罗拉导柱是每列罗拉连接的基准,其圆跳动公差影响罗拉转动及纱条质量。罗拉导柱的圆跳动标注如图1(b)所示,被测罗拉绕基准轴线(A-B)旋转1周时,测量仪器的最大变动量为径向圆跳动[14]。罗拉径向圆跳动的公差带如图1(c)所示,在垂直于基准轴线(A-B)的任一测量截面内,半径差为公差值t,且圆心在基准轴线上的2个同心圆之间的区域。根据FZ/T 93064—2017《棉粗纱机牵伸下罗拉》规定,罗拉导柱径向圆跳动公差值t≤0.015 mm。
1.2 基于机器视觉的径向圆跳动测量系统
由图1(b)所示的罗拉导柱圆跳动的精度要求,本文构建如图2所示的基于机器视觉的罗拉导柱圆跳动测量系统,以V型架为基准,牵伸罗拉绕着基准轴线转动,轴向无位移。由于罗拉的金属表面会反光干扰成像质量,因此采用背光成像方式,通过LED光源阵列提供均匀的背景光。由大恒水星工业相机在物距为250 mm条件下获取罗拉导柱图像,通过USB3.0接口实时传输至计算机,计算机显卡为NVIDIA GeForce GTX 1650,CPU为AMD A8—7680,内存为16 GB,硬盘为1.5 TSSD,在MatLab 2018环境中设计开发图像处理算法以实现罗拉导柱径向圆跳动的测量。

1—工业相机;2—镜头;3—相机支架;4—V型架;5—罗拉;6—计算机;7—面光源。图2 测量系统Fig.2 Measurement system
2 图像域下的牵伸罗拉导柱径向圆跳动模型
根据罗拉导柱径向圆跳动的定义,在图2的测量系统中,罗拉在V型架上进行等角度间隔旋转1周,罗拉导柱投影到图像域的二维轴截面如图3所示。

图3 罗拉导柱轴截面图像Fig.3 Cross section image of roller guide pillar shaft. (a)A frame image. (b)Binary image. (c)Subpixel edge detection

设基准实际轴线的最小二乘轴线为基准公共轴线,其方程见式(1):
y=kx+b
(1)
式中:y为基准公共轴线,x为基准实际轴线点,k为斜率,b为截距。
根据最小二乘原理,基准组成要素的边缘点pij(xij,yij)到轴线距离平方和最小,计算k、b,确定基准最小二乘轴线,则优化的目标为:
(2)
(3)
在垂直于基准轴线的任一测量截面内,max(rij(k,b))为最大跳动量,min(rij(k,b))为最小跳动量,则二者之差Δrij为:
Δrij=[maxrij(k,b)-minrij(k,b)]
(4)
本文以最小包容区域作为罗拉导柱径向圆跳动的评定方法,则被测要素的径向跳动f为:
f=maxΔrij
(5)
3 基于多项式拟合的罗拉导向柱边缘亚像素轮廓特征提取
罗拉导柱的轴截面图像如图3(a)所示,根据罗拉导柱图像灰度分布特点,采用最大类间方差法对其进行二值化处理,如图3(b)所示,罗拉导柱边缘特征明显,为了提高边缘检测精度,采用基于多项式拟合的亚像素检测方法提取罗拉导柱轮廓特征。
3.1 基于Canny算子的像素级罗拉导柱边缘检测
由图3(b)可知,罗拉导柱的边缘部分是图像的前景与背景变化最显著的位置,为精确得到罗拉导柱的上下边缘,对罗拉导柱进行Canny算子像素级边缘检测。在高斯卷积平滑的基础上,采用式(6)所示的2×2模板对平滑后的罗拉导柱图像进行x、y方向的二维一阶微分运算。
(6)
式中:Gx为x方向的梯度,Gy为y方向的梯度。
由此得到梯度的幅值M和方向θ为:
θ=arctan[Gy(x,y)/Gx(x,y)]
(7)
3.2 亚像素级检测
通过Canny算子得到的像素级边缘如图3(b)所示,罗拉导柱边缘特征近似平行线,因此采用基于多项式拟合算法进行罗拉导柱的亚像素级边缘检测。利用多项式函数对罗拉导柱像素级边缘进行最小二乘拟合,根据拟合函数确定罗拉导柱边缘轮廓。设三次多项式函数的表达式为:
f(x)=ax3+bx2+cx+d
(8)
当y=f(x)时,以测量值与回归值的偏差平方和S反映全部测量值与回归值之间的偏离程度[15-16],其表达式为:
(9)
对S进行偏微分计算,取极值条件为:
(10)
由式(10)计算多项式系数a、b、c、d,再根据条件计算罗拉导柱的亚像素边缘,如图3(c)所示。
4 实验分析
4.1 视觉系统标定
视觉系统的标定是决定图像测量精度的关键因素之一,标定主要是确定相机的内、外参数[17]。将光刻工艺加工的1 mm方格标定板固定在工作台上,保证罗拉导柱表面位于标定面上,标定板与相机位置关系及标定误差如图4所示,得到相机的内参数为:

旋转矩阵为:

平移矩阵为:
T=[-120.805 6,0.184 5,-0.408 8]
得到视觉测量系统的像素当量为0.0 041 mm/像素。
作为城市景观的焦点和城市公共空间的重要组成部分,小尺度空间水景在城市微观环境的整治中发挥着积极作用,是城市面貌的橱窗,也是评价人居环境的重要标准[12].小尺度空间水景的营建具有美学和生态学等多种意义,日益成为住宅小区景观设计的一大新亮点.东西方均对水景的运用进行了大量研究和应用实践,也涌现出了一批典型性的佳作,但单独针对小尺度空间研究水景应用的系统理论和代表性方案并不多.

图4 视觉标定Fig.4 Visual calibration. (a)Positional relationship; (b) Calibration error
4.2 罗拉导柱径向圆跳动的测量数据分析
4.2.1 测量数据分析
在计算罗拉导柱径向圆跳动时需对基准轴线进行拟合,在MatLab 2018优化工具箱中,对式(1)(2)采用最小二乘函数 lsqnonlin进行优化计算得到最小二乘基准轴线为y=-0.004 8x+1 181.2,如图5所示。
由图2所示的测量系统,以30°为间隔角将罗拉旋转1周,得到12帧罗拉导柱的轴截面图像,通过本文亚像素边缘检测方法得到如图5所示的罗拉导柱的上下边缘的亚像素边缘点数据,这些数据分布在基准轴线的两侧,通过局部放大可知,罗拉导柱边缘点数据不完全相同,在直径方向存在跳动,即径向跳动。

图5 边缘点数据分布Fig.5 Edge point data distribution
根据式(3)(4)得到如图6所示的某一帧罗拉导柱轴截面的最大跳动量与最小跳动量的差值变化曲线,得到测量导柱轴截面长度上任意一个测量截面的差值。根据式(5)计算得该帧轴截面的径向圆跳动为0.006 8 mm,小于设计的径向圆跳动公差0.015 0 mm,在公差范围内。

图6 差值变化曲线Fig.6 Distance difference curve
表1所示为罗拉导柱旋转1周得到12帧轴截面上的径向圆跳动测量值,以及人工采用千分表任选12个测量表面的测量值。
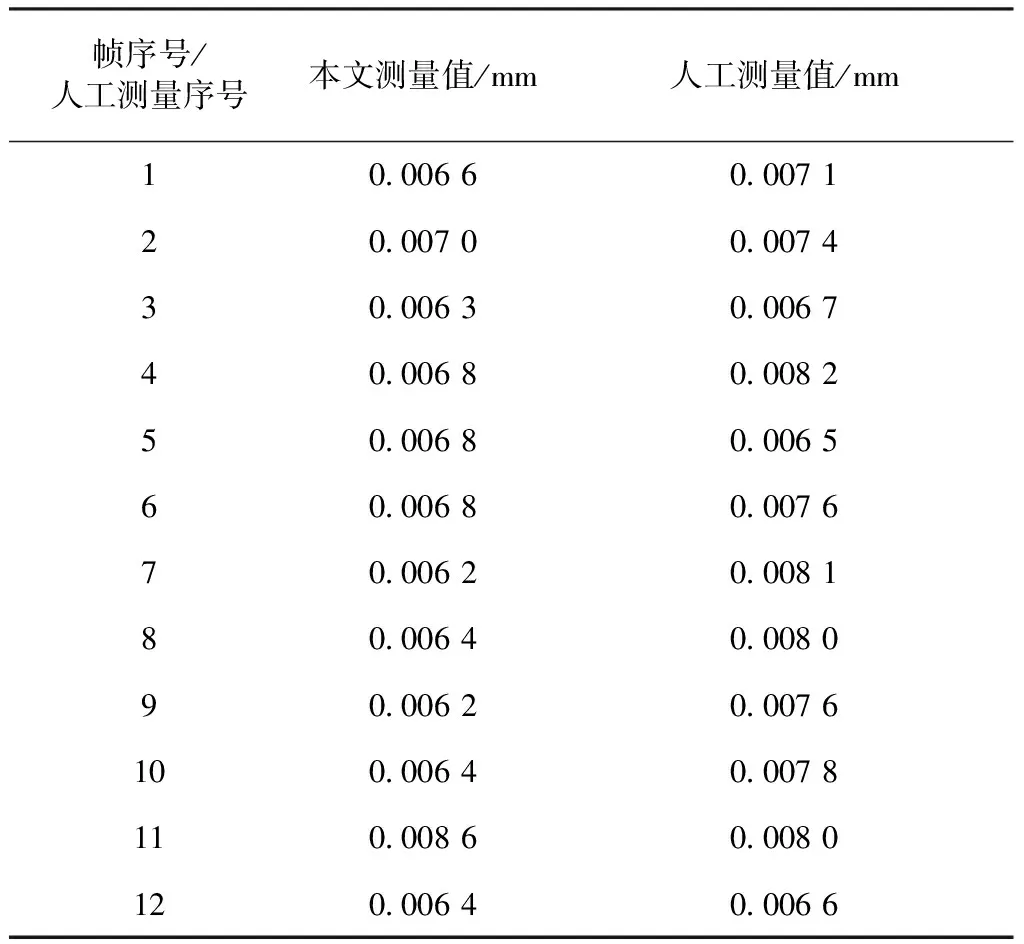
表1 罗拉导柱的径向圆跳动测量值Tab.1 Measured radial circular runout of roller guide post
由表1可知,本文方法与人工测量方法的测量值均小于径向圆跳动公差0.015 mm,表明该罗拉导柱的径向圆跳动合格。本文方法所测量的径向圆跳动的标准差为6.1×10-4,人工测量方法的标准差为6.6×10-4,可见本文测量方法达到了人工测量的精度,且能够定量表达罗拉导柱轴向表面的跳动状态,算法平均耗时0.67 ms。
4.2.2 误差分析
罗拉导柱的旋转角度直接影响测量精度与效率,旋转间隔角度越小,导柱面采样点越多,越能够表征罗拉导柱的表面特征,但是速度较慢,测量效率低;旋转间隔角度越大,导柱面采样点越少,影响罗拉导柱的表面特征,但是速度较快,效率高。本文在不同旋转间隔角度下对任取的3个罗拉导柱进行径向圆跳动的测量,结果如图7所示。
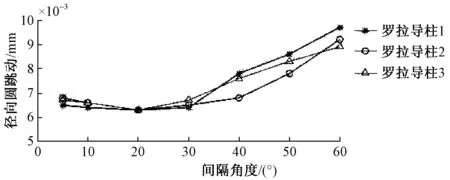
图7 不同旋转间隔角度的测量值Fig.7 Measured values of different rotation interval angles
由图7可知,在旋转间隔角度在10°~30°之间时,罗拉导柱的径向圆跳动测量值变化平稳,最大偏差为0.005 mm,说明间隔角度越小不会降低测量精度,且测量值之间的偏差很小。当旋转间隔角度大于40°后,由于间隔增加,轴截面序列图片的数量下降,导致测量的误差增大。因此为了保证精度及效率,旋转角度一般选取在20°~30°之间。
5 结 论
① 针对纺织针梳机牵伸罗拉导柱圆跳动的人工接触式测量检测精度不稳定、效率低等问题,提出基于机器视觉的牵伸罗拉导柱圆跳动检测方法,通过实验数据分析,本文方法测量的罗拉导柱径向圆跳动均在公差范围内,标准差为6.1×10-4,达到了人工测量的精度,算法平均耗时0.67 ms,具有非接触、快速、准确的特点,满足产品检测的需求。
②采用背光成像消除了罗拉导柱表面的光反射影响,以Canny算子对罗拉导柱的轴截面图像进行像素级边缘检测,利用三项式函数对罗拉导柱像素级边缘进行最小二乘拟合,确定罗拉导柱边缘轮廓分布位置,提高了亚像素边缘点的定位精度。
③建立了基于图像域的罗拉导柱径向圆跳动测量模型,对获取的罗拉轴截面图像,以基准要素罗拉颈圆柱面构建最小二乘基准轴线,根据径向圆跳动的定义,以最小区域法建立了罗拉导柱的径向圆跳动测量模型。

