基于双层规划的轨道交通接运公交线路优化模型

刘晓佳，李子木，卢罗兰

(集美大学 a.航海学院；b.海上交通安全研究所；c.文学院，福建 厦门 361021)

0 引 言

在轨道交通接运公交线路的相关研究中，接运公交线路设计问题一直以来都是国内外学者关注的热点。MARTINS等以乘客的出行时间总成本和常规公交运营总成本最小为目标，从多对一的需求模式出发，对接运公交线路的设计进行了探索。YU等建立双层模型研究公交线网服务单一铁路站点的接运规划问题，上层模型以系统总成本最低为目标，下层模型以乘客步行时间成本最低为目标，通过禁忌算法求解线路的停靠站点和停靠顺序，确定公交线网的接运方案。VERMA等以两阶段法为基础，以线路长度为约束条件，研究接运公交服务范围，利用最短路算法确定接运公交线路，利用遗传算法确定构成公交网络的接运公交候选线路。马壮基于距离衰减理论的可达性模型，应用GIS-栅格数据分析法探究预测社区公交客流的新方法。高明瑶等以由轨道交通站点始发的接运公交的客运周转率最大为目标，将接运公交线路长度、轨道交通站点剩余客流量、区段剩余通过量作为约束条件，利用改进粒子群优化(particle swarm optimization, PSO)算法对轨道交通接运公交线路优化模型进行求解。王佳冬等针对城市轨道交通与紧急换乘公交在突发运营中断情况下的换乘衔接问题，考虑换乘客流的脉冲特性，提出了针对应急接运公交时刻表和行车计划的综合优化模型。综上所述，在接运公交线路方面的研究还存在一些不足：国内外的研究大多集中在接运公交线路生成算法的单方面优化上；当前构建的一体化生成模型由于忽略了综合考虑多种交通方式下乘客出行的弹性需求和时间成本而缺少完整性；一般的迭代算法很容易进入死循环，迭代结果与预期不一致，优化效果不明显。本文针对多种交通方式下乘客出行的弹性需求，提出一种轨道交通接运公交线路双层优化模型：上层模型将接运公交线路生成的启发式算法(heuristic feeder route generation algorithm, HFRGA)与Floyd算法结合生成接运公交候选线路集合；下层模型根据广义费用最小原则，利用Logit模型对客流按照出行方式进行分配，最后以乘客出行总成本最低为目标，采用蝙蝠算法得到优化的轨道交通接运公交线网。

1 轨道交通接运公交线路生成模型

1.1 问题描述

由于轨道交通与常规公交定位不同，单一出行方式无法满足乘客的出行需求。在轨道交通网络形成前，轨道交通与常规公交之间的搭配不是很协调，许多乘客乘坐轨道交通往往需要通过较长时间的步行或者其他交通方式进行中转。因此，设计合理的轨道交通接运公交线路可以在一定程度上满足乘客的出行需求，减少乘客的出行时间。本文基于实地调查，重新规划轨道交通站点附近的公交站点，研究如何布设接运公交线路可以减少乘客的出行时间成本，使乘客出行换乘轨道交通更加便捷。

1.2 模型假设

根据轨道交通接运公交线路的运行特征，假设：(1)所有出行者均选择最短路径。(2)出行者乘坐的公交车可以直达轨道交通站点，途中不需要换乘。(3)出行者在出行前已经查得相关公交线路停靠站点等信息，不考虑走错路的情况。(4)每个需求点的需求量固定且已知。(5)乘客出行需求点与接运公交站点对应，忽略两点之间的距离。(6)不同接运公交线路上配备的车辆的车型相同，行驶速度相同。

1.3 模型变量

为研究时段集合，∈；为出行需求点集合，∈；为接运公交站点集合，∈；为接运公交候选线路集合，∈；,为从需求点到轨道交通站点的最短路径长度；,,,为在接运公交线路上需求点的出行者从公交站点到轨道交通站点的距离；、、分别为步行速度、骑行速度、接运公交行驶速度；,,为时段需求点的出行人数；w,,,、b,,,、tr,,,,,、v,,,为时段从需求点分别选择步行、骑行、在公交站点乘坐接运公交线路、私家车前往轨道交通站点的人数；w,,,、b,,,、tr,,,、v,,,为时段从需求点分别选择步行、骑行、接运公交、私家车前往轨道交通站点的人数比例；w,,,、b,,,、tr,,,、v,,,分别为选择步行、骑行、接运公交、私家车出行的时间成本效益函数；为接运公交线路非直线系数的上限；为接运公交线路的发车频率；、分别为接运公交线路发车间隔的下限和上限；为步行时间价值；为骑行时间价值；为乘客候车时间价值；为乘客在公交车上的时间价值；为私家车出行时间价值；为私家车油耗费用；为私家车停车费用；为出行者的出行费用效益系数；、分别为接运公交线路长度的下限和上限；为接运公交线路的路径长度；为接运公交线路两端点间的最短距离；，当接运公交线路在站点停靠时，=1，否则为0。

1.4 模型建立

一般地，乘客出行需要采用多种交通方式。本文通过分析多种交通方式下的乘客出行时间成本和客流分配情况，明确接运公交线路的约束条件，建立轨道交通接运公交线路双层优化模型。

1.4.1 上层模型

以乘客出行总成本最低为目标构建目标函数。在整个接运系统中，主要有步行、骑行、接运公交和私家车等4种出行方式。构建模型如下，其中下标∈，∈，∈，∈。

min|=++wa,+tr,+

(1)

其中，

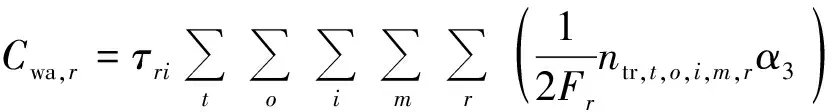
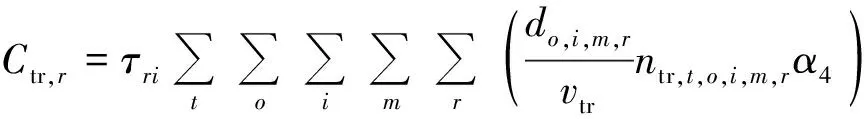
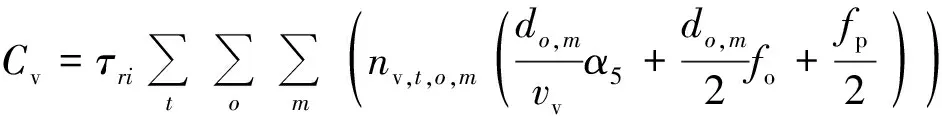
s.t.

≤≤

(2)

(3)

(4)

,,,≤

(5)

∈{0,1}

(6)

式(1)表示最小化整个接运系统乘客出行总成本。出行总成本包括步行者出行成本、骑行者出行成本、乘坐接运公交出行者出行成本和选择私家车出行者出行成本。乘坐接运公交出行者出行成本又包括出行者在公交站点候车时间成本wa,和出行者在车上的时间成本tr,。选择私家车出行者出行成本包括车辆行驶时间成本、油费和停车费。式(2)为线路长度约束，式(3)为线路非直线系数约束，式(4)为发车频率约束，式(5)为各公交站点到终点站的距离约束，式(6)表示为0-1整数决策变量。

1.4.2 下层模型

为合理分配客流，利用交通方式划分四阶段法中的Logit模型计算出行者选择不同交通方式出行的时间成本效益函数和客流分配比，将求得的客流分配结果应用于上层模型。

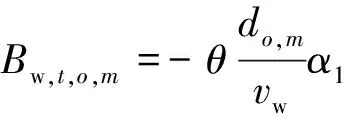
(7)

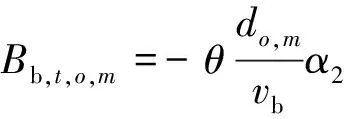
(8)

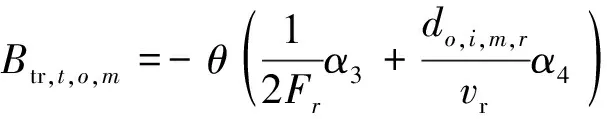
(9)

(10)

,,,=,,,,,=,,exp(,,,)×

(exp(w,,,)+exp(b,,,)+exp(tr,,,)+

exp(v,,,)),∈{w,b,tr,v}

(11)

w,,,+b,,,+tr,,,+v,,,=1

(12)

2 算法设计

2.1 生成接运公交候选线路集合

本文在HFRGA的基础上结合Floyd算法生成接运公交候选线路集合。首先在选定的公交站点中将客流需求大于平均需求的站点作为接运公交线路的起点，其次利用Floyd算法求得轨道交通站点与各接运公交站点之间的最短路集合，再将剩余站点分别插入，形成新的候选线路集合。生成的线路既满足了客流需求较大的站点，又增加了接运公交线路的客流量。接运公交候选线路集合生成流程见图1。

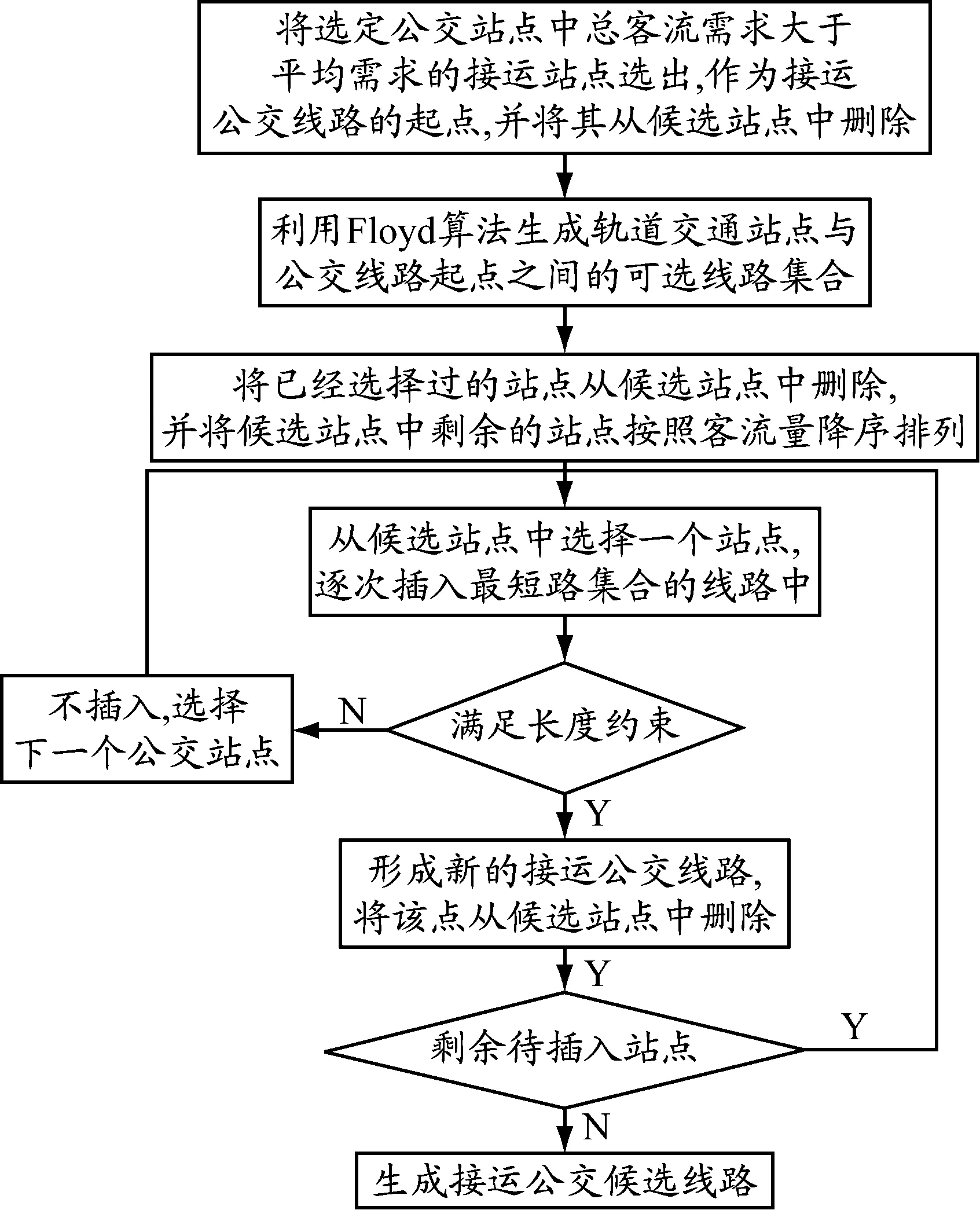
图1 接运公交候选线路集合生成流程

2.2 目标函数求解

蝙蝠算法的核心思想是将蝙蝠视为分布在搜索空间中的解决方案，通过模拟蝙蝠在复杂环境中准确觅食的机制来优化问题。每个虚拟蝙蝠都有一个随机的飞行速度,和位置,，蝙蝠所在的位置即为所求问题的解，同时蝙蝠有不同的脉冲频率、脉冲波长、脉冲响度和脉冲发生率,，蝙蝠在捕食时会根据被捕食对象的位置来调整脉冲频率、脉冲响度和脉冲发生率，直至到达目标位置或目标条件。因此，该算法的实质是平衡和调整算法的相关参数，实现蝙蝠群的动态行为，获得最优解。根据文献[10]，蝙蝠位置和速度的更新方程为

=+(-)

(13)

,+1=,+(,+1-)

(14)

,+1=,+,+1

(15)

式中；是蝙蝠的脉冲频率；、分别为的上限和下限；随机数为均匀分布在[0,1]内的一个常数；为目前找到的最优解。

,+1=,

(16)

,=,0(1-exp(-))

(17)

式中：和为常数，0<<1，>0，类似于模拟退火算法中冷却进程表中的冷却因素；,是蝙蝠的脉冲响度在时段的平均值。对于任意0<<1和>0，都有,→0，,→,0，→∞，这里，,0为蝙蝠的初始脉冲发生率。蝙蝠算法计算流程见图2。

图2 蝙蝠算法计算流程

3 实例计算

选用厦门市轨道交通一号线的文灶站周边公交站点和常规公交线路进行实例分析。轨道交通站点周围的客流集散量很大，公交线路重复较多，多个车次分摊同一线路的客流，且线路的布设不利于乘客出行换乘。通过调查分析，调整公交线路，合理分配客流，提升乘客出行的便捷性。

3.1 实例说明

图3为选定的抽象化后的公交线网示意图，站点1表示轨道交通站点(也为接运公交末站)，站点2～16表示接运公交站点(也为需求点)，站点之间的数字表示站间距，单位为km。需求点乘客出行需求会随着时间有所变动，选定一特定时间段进行调查，确保所选时段兼具道路特殊性和适用于其他时段的普适性。选取7:00—9:00早高峰时段，调查得到各需求点的出行需求，见表1。

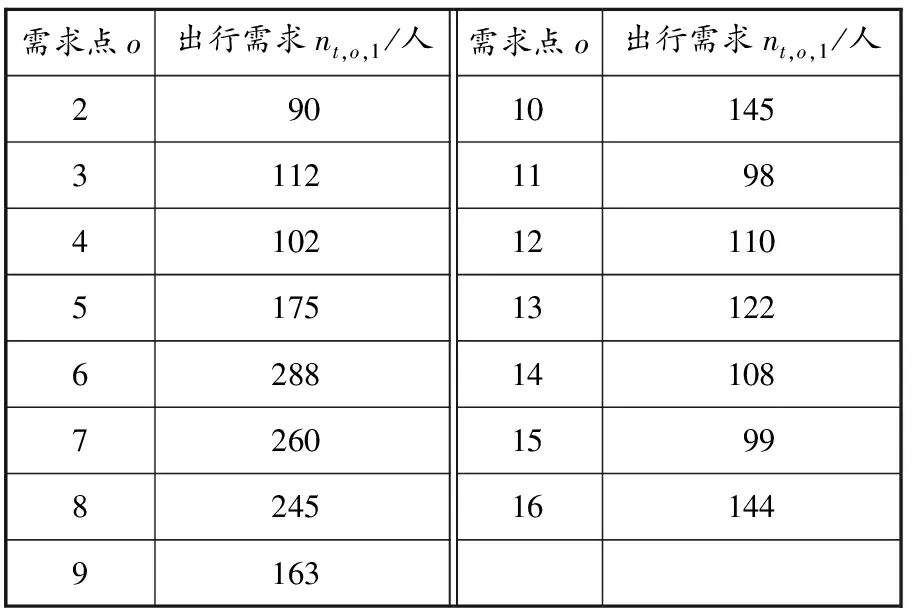
表1 7:00—9:00各需求点的出行需求

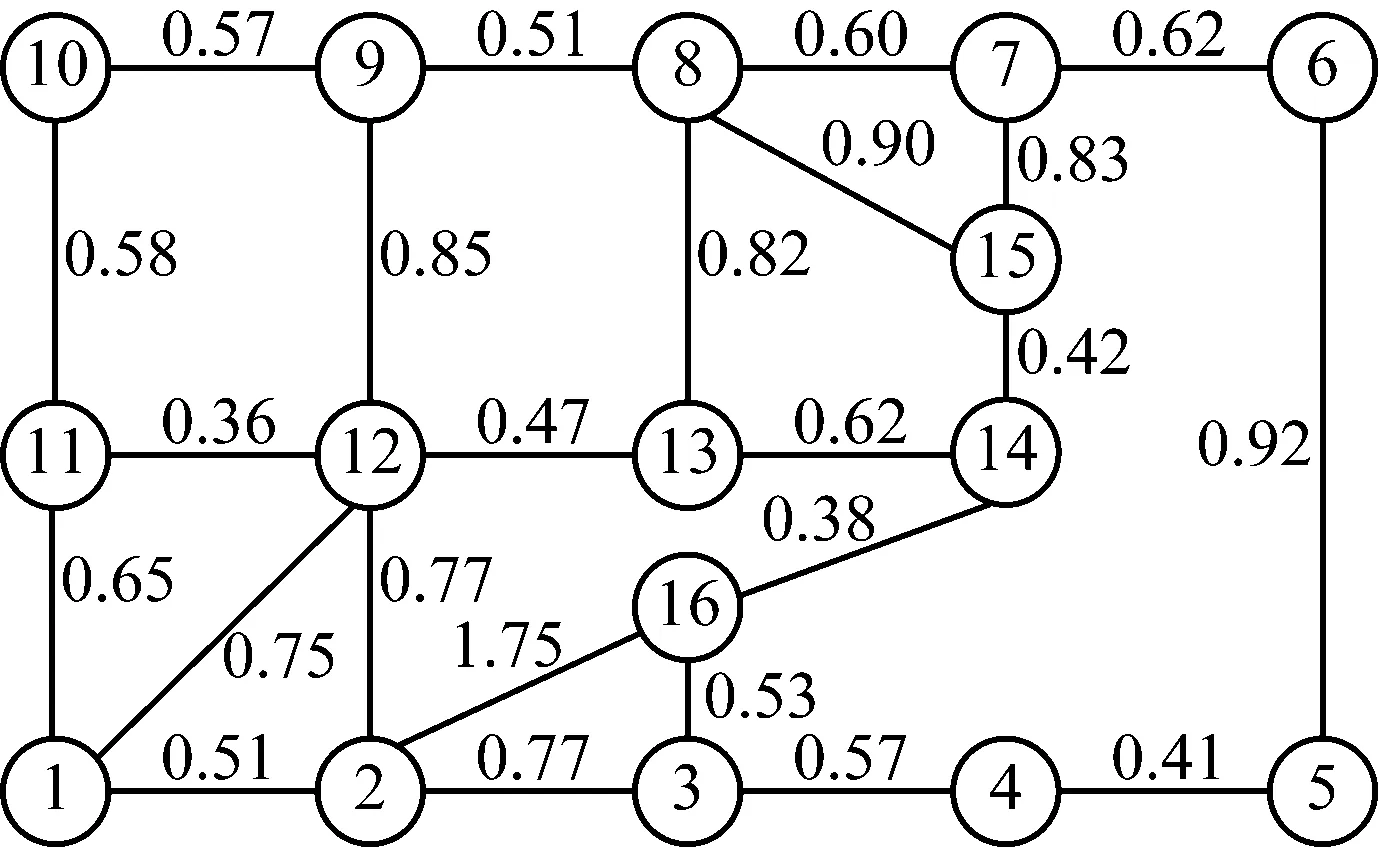
图3 选定的抽象化后的公交线网示意图

3.2 参数给定

在优化求解的过程中，经过多组实验将蝙蝠算法的参数设置如下：种群规模为80，最大迭代次数为200，脉冲响度的初始取值区间为[0.6,1.0]，初始脉冲发生率∈[0,0.5]，常数==0.98。

本文根据2019年厦门市城镇非私营人员平均年度工资96 193元计算单位出行时间价值。一年共250个工作日，按照每日工作8 h计算，平均时薪是52.5元。结合文献[10]与厦门的居民出行特征计算得到：工作商务出行的单位时间价值是平均时薪的1.33倍，从而工作出行的单位时间成本是69.83元/h。不同的出行方式会对出行时间成本造成影响：乘客的车内时间价值约占总时间价值的21%～25%，而候车时间价值约为车内时间价值的2～3倍，则接运公交出行者的候车时间价值为43.64元/h，在车上的时间价值为17.46元/h。私家车的出行成本为113.82元/h，其中涉及的私家车单位距离油耗费用为0.9元/km，单次停车费用为8元/次。

根据厦门市交通研究中心提供的实地调查数据及查阅文献[10,12]总结得到：接运公交线路的长度上限是8 km，下限是2.5 km；接运公交线路的非直线系数上限是1.5；接运公交的发车间隔上限是30 min，下限是5 min。其余相关参数见表2。

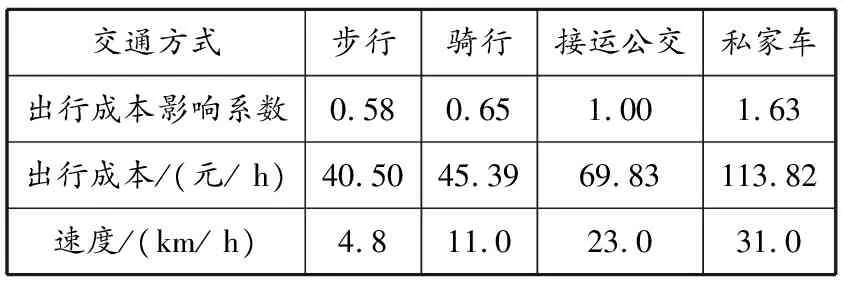
表2 早高峰时段各种交通方式出行成本和速度

3.3 优化结果与分析

根据第2.1节接运公交候选线路集合生成方法和客流需求相关分布情况，将站点6、7、8、9设为候选线路起点，待插入的点为2、3、4、5、10、11、12、13、14、15、16，考虑公交线路的非直线系数、线路长度、满载率等约束条件，利用Floyd算法生成接运公交候选线路集合，见表3。

表3 接运公交候选线路集合

通过双层模型求解各需求点与不同交通方式相应的客流分配比和出行需求，结果见表4。

表4 各需求点与不同交通方式相应的客流分配比

以乘客出行总成本最低为目标，通过蝙蝠算法在候选线路中搜索生成公交车接运方案。为分析模型的正确性和算法的效率，参照文献[13-14]的方法，设定接运公交线网中的接运公交线路数量为3条。当接运公交线路数量小于3条时，模型无解。当接运公交线路数量为3条时，接运公交线网由线路6-5-4-3-16-2-1、7-15-14-13-12-1和8-9-10-11-1组成，具体参数见表5。

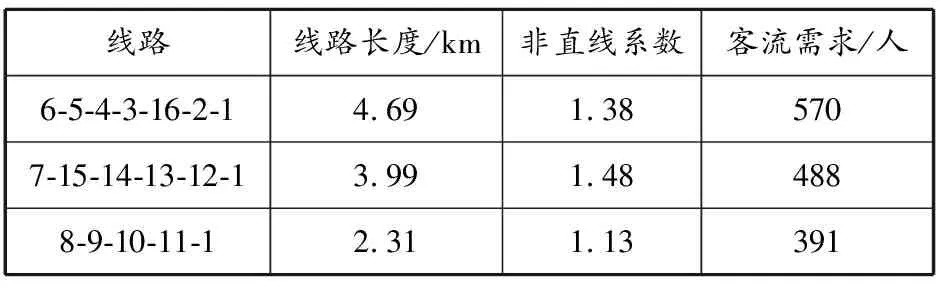
表5 优化后轨道交通接运公交线路

在原公交线网中，由于6、7、8、9公交站点乘客数量较多且无直达线路至轨道交通站点，乘客需要进行公交二次换乘或采取“公交车+步行”的方式才能到达，导致大多乘客放弃公交换乘，选择步行或骑行方式出行。通过计算得出，在原公交线网中，乘客选择公交出行的比例约为47.3%，乘客出行总成本约为16 108元。在生成的接运公交线网下，选择步行出行的人数占比为14.6%，选择自行车出行的人数占比为19.1%，选择接运公交出行的人数占比为64.1%，选择私家车出行的人数占比为2.2%，乘客出行总成本约为13 012元。与原公交线网相比，优化后的乘客出行总成本降低了19.2%，乘坐接运公交出行的人数上升了16.8%。合理布设公交车辆的停靠站点和顺序，可实现降低乘客出行总成本的目标，提高乘客选择公交出行的比例，提升乘客便捷性。

4 结 论

本文考虑了多种交通方式下乘客出行的弹性需求，以最小化乘客出行总成本为目标，建立接运公交线路生成与客流出行分配的双层规划模型。首先利用接运公交线路生成的启发式算法(HFRGA)和Floyd算法生成接运公交候选线路集合，再利用Logit模型对选择不同出行方式的客流进行分配。利用蝙蝠算法求解得到最终符合条件的接运公交线路方案。该研究成果不仅适用于规划轨道交通接运公交线网，还适用于“空巴联运”中机场大巴线路设计。本研究对公共交通一体化建设的完善和各交通方式的融合具有重要意义。后续研究可以在研究区域内增加轨道交通站点的数量，使需求模式扩展为“多对多”，加强对接运公交线路的发车频率、配套车型等方面的考虑。