新型净化器的室内不同位置PM2.5净化时间预测模型研究

赵慧森 樊乾乾 张浩然 黄婧阳 路 志 金梧凤

(天津商业大学天津市制冷技术重点实验室，天津 300134)

随着大气污染严重和雾霾天气的出现,PM2.5等大气污染物进入室内,加剧了室内环境污染[1]。现代人80%～90%以上的时间是在室内度过，室内空气中的污染物对人体健康产生很大影响[2]。而空气净化器作为一种新型家用电器,可有效控制室内污染物水平,改善室内环境空气质量,被越来越广泛地使用[3]。但是净化器在实际使用过程中，送风角度及速度等自身参数在不同条件的运行方式下，对室内不同位置人员区域的PM2.5颗粒物浓度的净化速度不同，所以对净化器不同条件下，室内不同人员位置处的PM2.5净化时间进行研究预测具有重要意义。

目前国内外学者对于空气净化器的研究主要集中在净化器摆放位置[4]、室内气流组织[5]、净化器自身参数[6]等对于PM2.5颗粒物浓度的净化效果方面。Atila Novoselac等人[4]研究了空气净化器位于室内不同位置时的净化效果，发现当净化器位置不同时，其对于颗粒物的总去除量差异较大，在极端工况下，最有效的净化器摆放位置的颗粒物去除量是最差摆放位置去除量的2.5倍。朱恺真等[5]对车间上送下回与侧送下回气流组织进行了模拟分析及实测验证，研究表明采用侧送下回气流组织,温度场和速度场分布更均匀,气流组织更合理。宣凯云等人[6]通过实验研究了空气净化器风量的影响因素，发现净化时间、PM2.5初始浓度、风向以及房间的密闭性均对空气净化器的风量有所影响。净化时间从1h变为0.5h时，净化风量增加了47%，说明净化时间越短，净化风量越大。PM2.5初始浓度和风量呈正相关关系。房间密闭性越好，所需净化器风量越小。

根据以上研究发现，目前对于空气净化器净化效果的研究，大多仅针对房间整体而言，但在实际房间各区域，空气净化器净化效果差异明显。净化器送风参数变化对净化效果影响较大，但其与室内不同区域净化时间之间的关系研究不足。本文在净化器送风仰角0°、大风速的运行条件下，利用Fluent软件模拟研究了室内各区域的PM2.5净化时间，同时研究了房间尺寸、吹风角度、PM2.5初始浓度、人员位置等影响因素对PM2.5净化时间的影响，再利用SPSS软件对研究资料进行回归分析，发现其不符合线性回归关系的基础上，又利用python软件对其进行非线性回归分析，最终建立该运行条件下的PM2.5净化时间预测模型。研究结论可为空气净化器实现人员区域优先净化和优化净化器运行模式奠定基础。

1 净化器影响因子的确定

1.1 净化器简介

研究所用净化器为LG某型号上送侧回滤网式净化器[7],净化器简图如图1所示。对于固定的空气净化器，能对室内颗粒物浓度产生影响的主要因素有：仰角角度和送风速度两大参数。

1-送风口A1；2-回风口B1；3-送风口A2；4-回风口B2；5-送风口A3；6-回风口B3

1.2 影响因子的确定

温度、湿度、风速等环境因素和空气净化器本身参数都会对室内颗粒物浓度产生影响。本文针对空气净化器本身参数作用下净化时间变化进行研究，综合考虑环境因素和人员位置对净化器的影响及室内墙壁对气流不均匀性的影响，最终确定对室内不同区域净化时间产生影响的因子有：PM2.5初始浓度ρ、房间面积η、仰角角度γ、送风速度v、送风方向α、房间长宽比Γ、人员距离L和人员夹角β。

影响因子作用方式如图2所示。

图2 各影响因子作用方式示意图

经理论研究确定，各影响因子取值如表1所示。

表1 影响因子的取值

根据空气净化器标准GB/T 18801-2015[8]，实验和模拟条件均定为：温度(25±2)℃，相对湿度(50±10)%，且无除净化器送回风以外的其他气流组织影响。

2 实验研究

本文中所进行的实验为验证实验，主要为验证空气净化器数值模型的准确性，并为模型的建立提供部分数据支持，完善修正模型。

2.1 实验台及设备介绍

参照国家标准搭建60 m3环境试验舱。实验舱分为内外两个舱室，内舱为6.15m×3m×3.2m型方体。舱体内壁、地板全部采用不锈钢材料，其表面光滑不结露，方便清洁，且可以降低空气污染物的吸附沉积，减少颗粒物自然衰减对于测试结果的影响。舱内设立有温湿度控制系统、空调系统、通风系统等，可达到对实验环境进行调控的要求。

实验设备参数如表2所示，各设备布置情况如图3所示。

表2 实验设备参数

1-空气净化器；2-Met One(AEROCET 531S)；3-粒子计数器;4-循环风扇；5-颗粒物发生装置(点烟器)

2.2 实验工况

实验台内舱环境因素设定为：温度25±2℃，相对湿度50%±10%，室内初始浓度350 μg/m3。

净化器运行模式选择为：0°仰角，最大风速，即送风口1风速为3 m/s，送风口2风速为3.5 m/s，送风口3风速为3.85 m/s。

2.3 实验测点布置

高度：人员静坐时1.1 m呼吸区。

送风方向上：每隔2.5 m布置一个测点，共2个测点。

实验测点布置如图4所示。

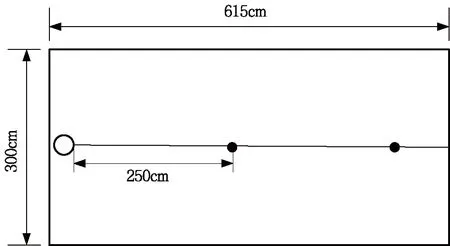
图4 测点布置图

2.4 实验方法

本次实验严格按照《空气净化器》(GB/T 18801-2015)[8]要求进行实验，共分为三个阶段：准备阶段、稳定阶段和测试阶段[9],为减小实验误差，进行了3组重复实验，对实验结果求取平均值。

2.5 实验结果分析

实验结果见图5，由图5可知，在净化器对2.5 m和5 m处实验测点的净化过程中，室内PM2.5浓度呈现出先降低后趋于稳定的净化趋势，5 m实验测点处PM2.5颗粒浓度下降速度整体比2.5 m处测点快，整体平均下降幅度达到6.59%。在第12 min时，5 m处实验测点较2.5 m处的PM2.5浓度下降幅度达到最大，为13.31%。

图5 2.5 m、5 m处测点PM2.5浓度随时间变化图

3 模拟研究

3.1 模型介绍

本节建立与实验舱相同的物理模型，并将其导入Fluent，然后对控制方程、边界条件、求解器进行确定。利用实验所得数据对模型的准确性进行验证。再根据更为准确的模型，通过改变房间尺寸进行拓展研究。

3.1.1 物理模型

首先建立了和实验环境舱相同的小型房间模型，运用 ICEM-CFD 对模型进行网格划分，并进行网格独立解试验。根据实验数据设定边界条件计算，逐渐增加模型的网格数量，对比不同网格数量下的计算结果的差异，减少网格数量对计算结果的影响，最终确定选用非结构化网格，网格数量为1 935 072，最小质量为0.1，最大质量为0.99。

3.1.2 数学模型的选择

为保证模拟研究的准确性，需要对CFD模拟的数学模型进行合理的选择与设置，如表3所示。

表3 数学模型设置

此外，为简化计算过程，对建立的模型进行了合理化假设，具体如下所示：

(1)不考虑房间壁面辐射换热的影响，房间内各壁面设置为绝热边界条件；

(2)室内空气为低速流，可视为不可压缩流体，符合Boussinesq假设[10]。

3.1.3 边界条件

为保证 fluent 软件模拟的合理性和可靠性，需要对边界条件和初始化条件进行设置，具体设置如表4所示[7]。

表4 边界条件及初始化设置

3.2 模型验证

与实验工况设置相同，将模型设置为室内温度25℃，相对湿度50%，空气净化器仰角角度0°，送风速度为3 m/s时，在室内PM2.5初始浓度为150 μg/m3的情况下，距离净化器2.5 m和5 m处测点在实验和数值模拟中PM2.5浓度随时间变化情况如图6所示。

实验数据和模拟数据的误差分析如表5所示。

由图6可以看出，当模型边界条件设置与实验测量值一致时，在PM2.5净化过程中，模拟与实验的PM2.5浓度变化趋势基本一致，均先降低后趋于稳定，净化速度保持一致。通过表5中的误差分析可以看出，距离净化器2.5 m和5 m工况下的实验值与模拟值的最大误差均小于10%。

表5 误差分析

综上所述，可认为所建立模型准确，可使用大房间的模型进行模拟。

3.3 模拟工况及测点布置

3.3.1 模拟工况

0°仰角时，净化器送风方向不作为影响因子，故影响因子仅剩PM2.5初始浓度ρ、房间面积η、房间长宽比Γ和人员距离L。本文利用正交试验法，将人员距离L作为因子，PM2.5初始浓度ρ、房间面积η、房间长宽比Γ作为水平，共确定了以下9种工况，模拟工况表如表6所示。

表6 模拟工况表

3.3.2 模拟测点布置

以净化器为原点，每隔30°布置一列测点，共7列测点；从净化器出发，0～3.5 m，每隔0.5 m布置一个测点，3.5 m之后，每隔1 m布置一个测点，共布置了52个测点。测点高度均为1.1 m。测点布置图如图7所示。

图7 测点布置图

3.4 模拟结果及分析

3.4.1 室内不同区域划分情况

在认为室内PM2.5浓度分布均匀的情况下，将室内PM2.5浓度降低至15 μg/m3所用时间称为净化时间[11]，作为对净化效率的评价指标。为探究室内人员在不同区域分布时空气净化器的最佳运行模式，本文对室内区域进行了划分，划分情况如图8所示。分别对每个区域内各测点的净化时间取平均值，以代表该区域在该运行模式下的净化时间。

图8 室内区域划分情况图

3.4.2 回归资料整理

通过模拟得到不同工况下各测点位置处的PM2.5浓度随时间的变化情况，进一步得到各测点位置处PM2.5浓度下降至15 μg/m3的时间，并将所有结果整理成回归资料，如表8所示。

表8 模拟结果

4 PM2.5净化时间预测模型的建立

利用模拟部分所得回归资料，通过SPSS软件和Python软件对模拟数据进行回归分析，建立模拟所设定的运行模式下PM2.5净化时间预测模型，并通过模拟数据进行验证。

4.1 多元回归分析

首先选用SPSS软件对回归资料分别进行多元线性回归分析，并通过R2指标检验模型的拟合程度，若R2>0.900则模型拟合程度好，继续对回归方程的显著性以及影响因子的显著性进行检验，若回归方程以及影响因子显著性好，即选用线性模型。若R2<0.900则模型拟合程度欠佳，利用Python软件，建立非线性回归模型，对回归方程拟合程度以及显著性进行检验，若满足条件即得到非线性回归模型。

首先选用SPSS软件的多元线性回归模型进行回归分析，检验模型的拟合程度，结果如表9所示。

表9 模型拟合程度

此种运行模式下不适合线性拟合回归，选用Python进行非线性回归分析。

4.2 模型多元非线性回归分析结果

模型建立过程中整个样本中随机选取10%的数据训练模型，用其余90%的数据测试模型。在该模型中trainscore:0.9773322390395321,testscore:0.9375507366890732。方程的拟合优度判定系数R-squared =0.977，模型拟合程度良好，P值为1.13e-79，远小于0.001，回归方程预测效果显著，如表10、11所示。

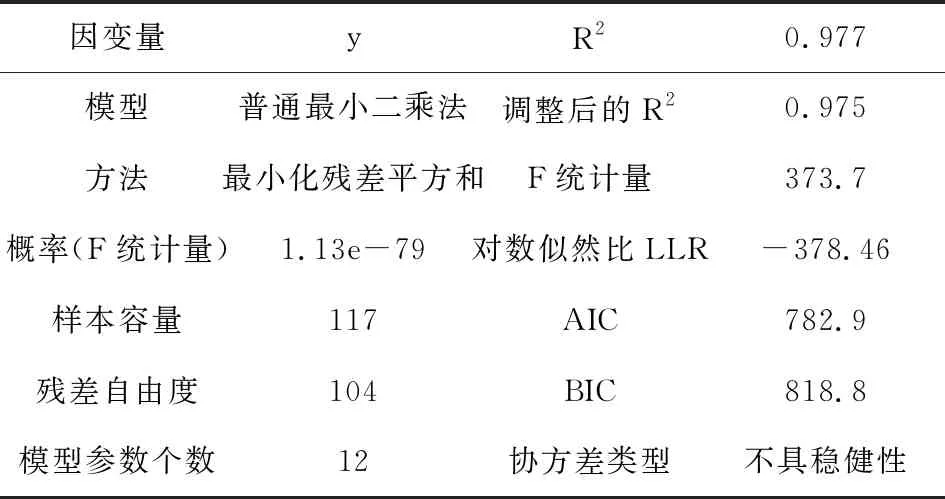
表10 模型多元非线性回归分析结果(1)

表11 模型多元非线性回归分析结果(2)

通过以上分析可以得到运行模式下，PM2.5净化时间与各影响因子之间的关系式如式：

t=-1.38η-64.8Γ-0.966ρ-14.8L-0.00711η2+0.702ηΓ+0.0169ηρ+0.105ηL-1.94Γ2+0.252Γρ+2.27ΓL-0.0226ρ2+0.0439ρL+0.133L2

式中各参数取值范围见表1中各影响因子取值范围。由关系式可知，PM2.5净化时间与各影响因子之间呈非线性关系：与房间面积及其平方、房间长宽比及其平方、PM2.5初始浓度及其平方、人员距离呈负相关。与房间面积和房间长宽比乘积、房间面积和PM2.5初始浓度乘积、房间面积和人员距离乘积、房间长宽比和PM2.5初始浓度乘积、PM2.5初始浓度和人员距离乘积、人员距离的平方呈正相关。

4.3 模型影响因子贡献率

模型中各影响因子对净化时间的贡献率如表12所示，房间面积对人员处净化时间的影响贡献率最大，为30.08%，人员距净化器的距离对人员处净化时间的影响贡献率最小，为20.07%。可见改变房间面积对净化时间的影响最大。

表12 模型影响因子贡献率

在空气净化器的实际使用过程中，房间面积一般是固定的，故在计算各影响因子的贡献率时，不需要考虑房间面积的影响因子，在该运行模式下，其余影响因子对净化时间的贡献率如下：房间长宽比对于PM2.5净化时间的影响程度最大，由25.01%增加到35.76%；PM2.5初始浓度贡献率次之，由24.85%增加到35.54%；人员距离的贡献率最低，由20.07%增加28.70%。可见，影响因子房间长宽比和PM2.5初始浓度对PM2.5净化时间的影响程度显著，故在净化器实际使用过程中，应着重考虑PM2.5初始浓度和房间长宽比的影响。

5 结论

(1)研究得到了净化器0°仰角、最大风速模式下符合非线性回归关系的净化时间预测模型。其中PM2.5净化时间与各影响因子之间呈非线性关系：与房间面积及其平方、房间长宽比及其平方、PM2.5初始浓度及其平方、人员距离呈负相关；与房间面积和房间长宽比乘积、房间面积和PM2.5初始浓度乘积、房间面积和人员距离乘积、房间长宽比和PM2.5初始浓度乘积、PM2.5初始浓度和人员距离乘积、人员距离的平方呈正相关。

(2)模型中房间面积对人员处净化时间的影响贡献率最大，为30.08%，人员距净化器的距离对人员处净化时间的影响贡献率最小，为20.07%。可见改变房间面积对净化时间的影响最大。

(3)当房间面积固定时，房间长宽比对于PM2.5净化时间的影响程度最大,由25.01%增加到35.76%；PM2.5初始浓度贡献率次之，由24.85%增加到35.54%；人员距离的贡献率最低，由20.07%增加28.70%。可见，房间长宽比和PM2.5初始浓度对PM2.5净化时间的影响程度更显著，故在净化器实际使用过程中，应着重考虑PM2.5初始浓度和房间长宽比的影响。