基于旅客时间价值的高铁民航竞争空间距离研究
孟海洋,陈思琦 ,李红昌* ,侯远舟
(1.滨州学院经济管理学院,滨州 256600;2.北京交通大学经济管理学院,北京 100044)
旅行和通讯网络被定义为人类促进和参与社会网络必不可少的社会资本,而在其中,高速铁路作为一个国家最具普适性的重要基础设施及市民出行的重要交通工具,在任何一个国家的经济发展及民生发展中都扮演着举足轻重的角色。自2008年以来,中国把高速铁路的规划与建设作为国家重大战略性建设项目。目前,我国高速铁路营业进程已经达到4万km,中国运输行业所面临的客运及货运的巨大压力将得到有效的缓解。目前,在高速铁路运行密集的地区大部分都属于经济发达地区,是民用航空的主要消费市场,随着高速铁路的全面提速,民用航空市场将不得不面临客源分流营业额下降的压力,同时,原有的交通方式运输分担率的也会随着市场的自我调节进行重新分配,给整个航空运输产业造成难以恢复的影响。
1965年,诺贝尔经济学奖得主贝克尔提出对出行行为进行分析[1],第一次提出时间价值的概念,他认为日常生活中的消费时间是每个人都不能避免的要素投入,并建立家庭生产的效用函数来分析家庭如何进行时间分配,以获取效用最大化。这种将时间变量引入消费者效用函数的方式为之后的家庭生产理论的时间分配理论奠定了基础。20世纪70年代以后,时间价值逐渐受到关注并作为研究对象应用于工程实践。非集计模型、效用最大化理论,是当时最热门的计算时间价值的方法。90年代以后随着各国学者对于时间价值这一概念研究的不断深入,研究的角度呈多元化的态势发展。
Jiang等[2]从交通方式与路径选择的角度对时间价值与消费者效用进行了研究,将出行者所选择的交通方式,花费的时间以及工作时间、休息时间等纳入到出行者的效用函数中,得到交通方式改变所产生的时间价值节省应该包括旅行成本随时间变化所产生的价值的结论。Flügel[3]则重点从出行者类型的不同(包括出行目的、可支配收入、社会地位等)以及出行所采用的方式(如舒适程度不同)不同出发,对时间价值节省的影响因素进行探究。他利用控制变量的方法分别计算出不同类型出行者与不同出行方式的时间价值节省的变化情况,使得到的结果更加精确。也有一部分学者将研究重点放在了完整的位移链条上,他们认为完整的位移以及位移时间的除了在交通工具上所花费的时间之外还包括了行走时间、等候时间等衔接时间,且发车频率(尤其是在公共交通领域)也会对消费者出行的时间价值造成影响。Wardman[4]利用估值回归模型探索公共交通与小汽车的时间价值与行走时间、等候时间、间隔时间的价值之间的关系。他认为行走、等候及间隔的时间价值受到旅途距离的影响;使用者的类型以及收入的多少也决定了旅行的时间价值;然而与前人结论相反的,他认为行走时间价值与等候时间价值并没有显著的高于在交通工具上的时间价值,且它们多少会受到间隔时间价值的影响。Sheikh等[5]基于连续9个月高峰时段穿过车道的出行数据,对南行与北行车辆的出行时间价值、下午峰值等进行测算。Schmid等[6]应用RP/SP调查法、混合Logit测算方法,研究了选择不同出行方式的旅客的时间价值(value of time,VOT)水平,结果发现,在所有接受调查用户中,选择公共交通工具的VOT是最小的,其次为出租车、私人汽车。白雪莲等[7]运用混合Logit模型,测算了基于个人支付意愿的航空旅客通达机场时间价值。李晓津等[8]利用收入法和调查法、混合Logit模型,以北京—太原—成都客运通道为例,研究了公务出行、休闲出行、求学出行三类旅客时间价值。袁乐凯等[9]基于对轨道车厢内拥挤以及早到和晚到成本的考虑,构建了轨道交通廊道中的出行动态均衡模型,对模型算法和出行时间价值对乘客出行分布的影响进行了分析。
在高铁和民航竞争研究方面,薛亮等[10]从旅客时间价值分析的角度对人们出行方式的选择进行了比较,将不同交通方式下所产生的效用进行比较,分析了三种交通运输方式(航空、公路、铁路)在旅客综合效用值下的目标市场。赵坚等[11]运用节省旅行时间价值模型计算出了高铁相对于民航具有绝对优势的旅行距离,即在时间与费用上都小于民航的旅行距离范围,得出在该范围中旅客更偏向于选择高铁出行的结论,并深入分析了影响旅行时间的主要因素及大国节约旅行时间价值的特殊问题。谭向东[12]从产业经济学的角度对高铁与民航的产业发展进行了对比分析,分析的角度囊括了时间价值、旅客出行效用、出行费用、准点率等,将民航与高铁的竞争空间进行了层次性划分,并分别在短期、中期、长期的角度对民航与高铁的竞争策略提出了政策性建议。牟振华等[13]通过建立基于Logit动态的交通方式选择演化博弈模型,对高铁提速情况下用户出行选择高铁与民航动态适应过程进行了探究。曹炜威等[14]利用2019年高铁列车和航班时刻表数据搭建了无向网络模型,比较分析了中国高铁与民航网络拓扑结构特征,结果发现高铁和民航网络的特征路径长度与集聚系数较为接近,不过高铁有着更大的网络密度、更强的紧凑性。Li等[15]分析了高铁旅行时间等因素对民航的影响。Zhang等[16]对高铁与民航的时间竞争及服务质量竞争等进行了全面性的回顾。Zhu等[17]分析了民航航班延误对高铁民航竞争的影响。但总体来说,对于旅客出行边际时间价值节约如何影响到了高铁民航的有效竞争空间距离的研究尚不多见,随着旅客时间价值、枢纽接驳时间、交通旅行速度等的变化的情景分析也不多见。
针对现有研究不足,立足中国交通建设如火如荼的大背景,现建立边际时间节省成本的计算模型,以旅客的旅行时间价值与民航与高铁间边际节省时间成本之间的关系为切入点,通过对旅客的旅行时间价值的评估与数据模拟分析,对民航与高铁的竞争力有效空间距离进行分析比较,深入分析基于时间价值的高铁与民航竞争距离问题,以期为我国高铁与民航发展提供有益参考。
1 模型构建
旅行时间价值是由于旅客在旅途中耗用的时间存在机会成本所产生的价值,它是人们对出行时间的一种评价。在假设消费者是理性经济人的前提下,微观经济学消费者行为理论是按照个人效用最大化原则来选择最佳交通工具及其最优出行组合方式。
1.1 基于效用最大化模型的时间价值
旅行时间价值可分为两类:一类为旅客行为时间价值,侧重考察旅客行为偏好价值;一类为旅客资源时间价值,偏重于交通运输投资项目的效益和费用分析。本文中研究的旅行时间价值为前者,强调的是旅行时间价值所产生的机会成本,基于旅客选择交通方式的角度进行测算。构造旅客交通方式选择行为的效用函数:

(1)
Uiq=∑θikXikq
(2)
式(1)代表交通方式选择的效用。式(2)中:θ为仅随旅客出行方式变化而变化的参数;X为运输方式或旅客的社会经济特性;k为运输方式或旅客的特性集合。设ε服从Gumbel分布,可推导出旅客选择行为的Logit模型。设旅客q选择其效用最大化的方式Ai,即
Uiq-Ujq≥εjq-εiq
(3)
则旅客选择交通方式Ai的概率Piq为
Piq=P{εjq≤(Uiq-Ujq)},∀Ai∈A(q)
(4)
假设随机误差项ε服从参数为(δ,μ)的Gumbel分布,推广到(ε1,ε2,…,εk),k个独立的Gumbel分布,可得Logit模型的一般化表达式:
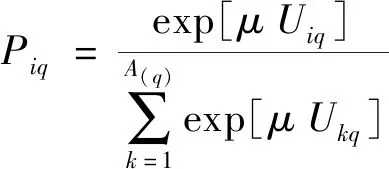
(5)
假定μ=1,式(5)可简化为
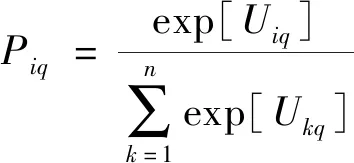
(6)
与综合费用最小模型的处理方式相似,将式(6)用极大似然法进行处理,并进行求导,可得似然方程组:
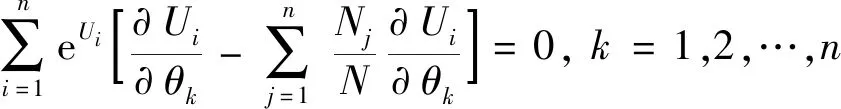
(7)
当仅有两种选择时,n=2,即有N=N1+N2,经过计算可得
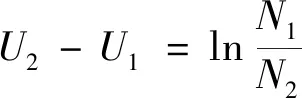
(8)
考虑出行时间和出行费用大的旅客时间价值,效用U的常见表达式为
Ui=ai+bipi+citi
(9)
式(9)中:ai、bi、ci为待估参数;pi、ti分别表示为旅客所选第i种交通方式的费用和花费的时间,时间价值VOT(i)可表示为
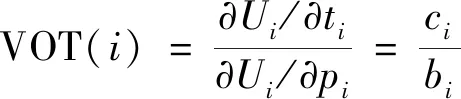
(10)
将式(10)代入式(5),可得
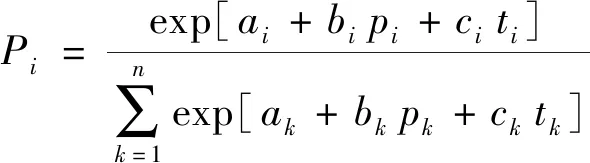
(11)
式(11)中:Pi为旅客在n种可选择的交通方式中选择第i种的概率。通常情况下,式(11)中的系数视为等值,即bk=b、ck=c。对i、j两种交通方式进行比较可得如式(12)所示线性回归模型:
lnPi/Pj=Δaij+bΔPij+cΔtij
(12)
式(12)中:Δaij=ai-aj表示交通方式i相较方式j具备的优越性,包括舒适程度、安全性、服务水平等,ΔPij、Δtij与Δaij相似,分别表示两种交通运输方式的价格差与所花费的时间差,则旅客的时间价值可以表示为
VOT=c/b
(13)
由于式(12)中的系数b、c并不能通过计算直观地得到数值 ,想要得到旅客的时间价值仍然需要大量的数据进行复杂的计算,因此一些学者将两种模型结合处理,对旅客时间价值的计算过程进行简化。
简化后的旅客效用函数可表示为
Ui=ai+pi+VOT·ti
(14)
旅客选择两种交通方式的概率分别为Pi、Pj,且Pi+Pj=1,因此,式(14)可化为
lnPi/Pj=Δaij+ΔPij+VOT·Δtij
(15)
1.2 旅行时间价值与边际时间节省成本模型
式(15)中的时间价值VOT可用收入法进行计算。收入法所表示的意义是出行所花费的时间使旅客个人的机会成本受到了损失,也就是说出行所花费的时间占用了旅客本来可以用来工作的时间,从而使旅客由于工作时间的减少而导致了其收入的减少,该方法的计算公式可以表示为
VOT=Y/T或VOT=M/t
(16)
式(16)中:Y为消费者的个人年收入;M为消费者的个人月收入;t为消费者的月均就业小时数。该方法能够较好的反映出用个人收入支付出行费用的客流群的时间价值,且计算方法及数据的采集较为方便直接。
旅行时间价值被看作是旅客在旅行过程中时间花费的机会成本,基于经济学中的边际分析法,判断旅客是否要付出额外的旅行费用来减少旅行时间的关键是看旅客所节省下来的时间用于生产所创造的财富或该时间用于休闲所产生的效用是否大于因选择更快捷的交通方式需要额外付出的货币损失。因此,判断旅客是否要选择支付更高的费用来缩短旅行时间的临界点为当边际时间节省成本(MTSC)等于旅客时间价值(VOT)时,即
MTSC=VOT
(17)
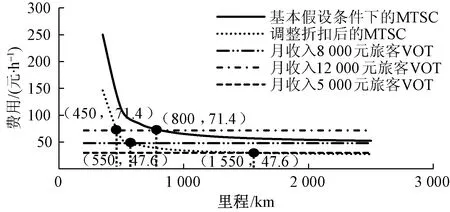
从旅客所获得效用的角度对该公式进行分析说明:旅客判断是否改变出行方式的临界点为使他休闲时间的边际效用等于旅行时间的边际节省成本。当MTSC>VOT时,旅行时间的边际节省成本大于休闲时间的边际效用,即旅客从额外一单位休闲活动中所获得的效用不足以弥补为增加休闲活动而付出的损失,因此旅客将延长旅行时间而减少休闲活动的时间。反之,当MTSC 因此,本文中判断旅客更偏向于选择高铁还是民航出行的依据为判断旅客的旅行时间价值与边际时间节省成本的大小关系。当MTSC>VOT时,旅客更偏向于选择高铁出行;而当MTSC 基于本文中研究重点,边际时间节省成本为高铁与民航的费用差与旅行时间差的商,因此MTSC可以表示为 (18) 式(18)中:PA为旅客乘坐飞机所需要支付的费用;PR为旅客乘坐高铁所需要支付的费用;TA为旅客乘坐飞机所需要花费的总时间;TR为旅客乘坐高铁所需要花费的总时间。 民航的定价特点为:根据《关于民航国内航空运输价格改革方案的起草说明》,国家发改委和民航总局根据民用航空运输的社会供求状况、承受能力以及平均成本,将民用航空的基准价确定为平均每人0.75元/km。航空公司可以在基准价的基础上最多上浮25%、下浮40%的范围内确定不同航线的机票价格。 高铁的定价特点为:高速铁路的定价遵循递远递减原则,高速铁路的平均运价率基本维持在0.45元/km左右,随着里程的增长,高铁线路的平均运价率逐渐降低,里程最长的京广线平均运价率为0.376元/km。由于高速铁路的运营范围变化跨度大,因此不同线路的总票价也随着运营里程的变化呈现出明显不同,部分线路的票价会高于全国高铁票价平均水平。 由于民航与高铁的定价策略都与运营里程与运价率有直接关系,因此有: PA=pa(Sa)Sa PR=pr(Sr)Sr (19) 式(19)中:pa(Sa)与pr(Sr)分别表示民航与高铁某段线路的运价率,用与里程相关的函数表示;Sa与Sr分别表示民航与高铁的里程数。 “小说中适度的留白或省略是必要的,原故事其实讲得够多了。按照海明威的冰山理论,作家去写露出水面八分之一的冰山锥就够了,剩下的八分之七读者自能领悟。卡佛更进一步,他的小说出现了大量的断裂、未知乃至不可解释,这使他避免成为海明威的跟班而自成一家。该小说家面面俱到的写法,完全是画蛇添足——我认为盯梢者跟那个女人结婚的事,留白会有更大的想象空间。况且,那个女人的新一任丈夫,真是那个盯梢者吗?还只是小说家的一面之辞?尽管原故事处处暗示他就是,但小说家一口咬定就失之武断。即使是也不必公仔画出肠,真是可惜了,小说家应当删改。” 根据高铁与民航票价的定价特点有: (20) (21) 而对于TR、TA,有: (22) 因此MTSC可表示为 (23) Sa、Sr分别为民航与高铁运营的里程数,由于高铁存在中途的停靠站点,且陆路轨道的建设会受到沿线设施的限制,一般情况下飞机的里程为两城市间的直线距离,而高铁则为起点城市到终点城市的“走形”距离,因此Sa≠Sr,表1列举了中国目前已开通的高铁线路中的10条线路里程数与相应的航空里程数。 表1 高铁与民航各线路里程数Table 1 High-speed rail and civil aviation route distance 各线路由于地势地形等原因,高铁与民航线路相差里程数互不相同,为了方便计算,这里取平均值15%进行计算,即Sr=Sa(1+15%)。 高铁的运行时速为250~300 km/h,最高可达350 km/h,考虑到停靠站点的停留时间,高铁运行的平均时速按235 km/h进行计算;民用航空飞机的运行时速为700~800 km/h,考虑到起飞降落等因素,飞机运行的平均时速按680 km/h进行计算。由于当前航空公司经常不定期推出折扣票价,但考虑到燃油附加费、保险费等其他费用的支出,设ε(s)=0.9进行计算,并设Δt=1,于是有: (25) 图1为根据式(25)画出的边际时间节省成本的走势图,根据该走势图可以看出民航相对于高铁的时间价值节省成本呈现出随着里程的增加递减的规律,这也符合经济学中边际成本的变化规律。由于受到最短运营里程的限制,因此该走势并不是从0 km开始计算,由于不同收入群体的旅客具有不同的时间价值,因此将根据该走势图及边际时间节省成本与不同旅客的时间价值之间的关系对高铁与民航的竞争性做解释说明。 图1 边际时间节省成本走势图Fig.1 Marginal time saving cost trend 2.3.1 高铁的绝对优势距离 对于旅客而言,出行耗费的不仅有货币成本,也有时间成本,时间和金钱对于旅客来说都属于稀缺资源,因此消费者会根据旅行时间、旅行费用、以及个人偏好等因素综合考虑来选择能够使其出行效用达到最大化的交通运输方式。由于与民航相比高铁的绝对优势距离属于短距离线路,因此在分析高铁的绝对优势距离时,忽略由于民航高铁舒适性、服务性等因素而造成的消费者个人偏好不计,这里将高铁的绝对优势距离定义为消费者选择高铁或民航出行所花费的时间相等时的距离,因为同一条线路上,高铁的价格低于民航的价格,而民航在这一距离范围内的旅行时间上也不能凸显出优势,因此在这一距离范围内,选择高铁出行时消费者的最优出行方案。 这里所说的旅行时间是指总旅行时间,由2.1节可知,tr、ta分别表示旅客在乘坐高铁或民航除列车或飞机运行之外的额外花费的时间,包括旅客从出发地到达高铁站或机场的时间;旅客从高铁站或机场离开到达目的地的时间;以及候车、安检及其他等候时间等。由于机场多位于郊外,旅客从出发地到达机场的时间普遍要长于从出发地到达高铁站的时间,且由于旅客在乘坐飞机时需要进行较为严格的安全检查及行李托运,需要提前到达机场,因此有ta>tr,假设Δt=ta-tr=1时,高铁的运行时速为250~300 km/h,考虑到列车需要停靠站,高铁的平均时速按235 km/h进行计算,飞机的运行时速为700~800 km/h,考虑到飞机的起降过程,飞机的平均时速按680 km/h进行计算。因此,高铁的绝对优势距离S=(ΔtVaVr)/(Va-Vr)=360 km。考虑到有些城市的高铁站位于城市中心,而机场设在郊外,从城市到机场的时间会远多于到高铁站的时间,因此假设当Δt=ta-tr=1.5时,高铁的绝对优势距离S=(ΔtVaVr)/(Va-Vr)=539 km。因此,里程在360~539 km以内的线路,高铁具有绝对的竞争力。通过图一也可以看出,当里程在500 km左右范围内,MTSC的水平极高,需要具有非常大的消费者出行时间价值群体才有可能选择民航而不是高铁出行。 2.3.2 高铁的相对优势距离 情景1:边际时间节省成本对旅客出行决策的影响。在现有考虑的影响时间价值因素下,由于收入因素为最主要的影响因素,为了更有效的对时间价值进行分析,现根据旅客的收入层次将旅客进行分组。由于高铁还处于全面建设阶段,当前已开通线路多位于经济较发达城市,且在不考虑廉价低折扣机票的情况下,现阶段高铁和民航所面向的消费者仍然属于收入较高的人群,因此将分组定位在经济发达地区人均收入水平之上。分组情况如表2所示。 表2 消费者分组Table 2 Passenger groups 由于目前已有42个城市人均收入水平达到90 000元以上,因此选月收入8 000元将消费者收入进行划分符合实际情况。图2为在当前假设前提下MTSC与消费者旅行时间价值的关系。 由图2可以看出,对于人均月收入低于8 000元的旅客来说,时间价值始终低于民航对于高铁的MTSC,这部分旅客没有为了减少旅行时间而选择民航出行的意愿;而对于人均月收入大于12 000元的旅客来说,当MTSC小于其时间价值时,即当其出行的距离大于800 km时,选择民航出行所得的效用会大于高铁,因此旅客会选择民航出行,而当其出行距离小于800 km时,旅客依然把高铁作为最优的出行选择。因此,在当前假设条件下,民航只有在里程超过800 km的航线中,面对高端消费群体才具有竞争力。 情景2:衔接时间对旅客出行决策的影响。设若航空公司为了提高自身的竞争力,采取一些措施减少旅客搭乘飞机出行的衔接时间,如设置绿色通道加快旅客安检速度,开通机场专线巴士减少旅客从出发地到达机场的时间等,此时Δt=0.5 h,则在其他条件不变的情况下,MTSC的计算公式变为 (26) 则MTSC的变化趋势如图3所示。 图3 调整Δt后的MTSC与VOTFig.3 MTSC and time value after the adjustment of Δt 可以看出,Δt经过调整之后,新的MTSC水平整体下降,与月收入12 000元旅客VOT的交点明显向左移动,表现出月收入水平在12 000元左右的乘客愿意乘坐飞机的里程数减小,即当这部分旅客的出行距离大于450 km时,民航就成为了他们出行最优的选择。同时,对于收入在8 000~12 000元的旅客随着出行距离的逐渐增大,与调整前的情况相比,将会有更多的旅客愿意选择民航出行;而对于月收入水平在8 000元及8 000元以下的旅客来说,出行距离在1 800 km左右时,MTSC与这部分旅客的VOT趋于相等,即在1 800 km以上的出行决策上,这部分旅客有可能会选择民航代替高铁出行。 情景3:出行费用对旅客出行决策的影响。面对高铁日益严峻的竞争压力,多家航空公司都采取降价打折的方式吸引消费者,尤其是当处于出行淡季的时候,折扣后的机票价格甚至会低于高铁的票价,由于超低价机票仅仅属于特例情况,为了对价格的分析更具有普适性,现将MTSC计算公式中的折扣系数ε(s)由之前的0.9调整为0.8,调整后的MTSC的计算公式可表示为 (27) 则MTSC的变化趋势及VOT之间的关系如图4所示。 图4 调整折扣后的MTSC与VOTFig.4 MTSC and VOT after the adjustment of discount coefficient 可以看出,当民航的票价在基准价的基础上折扣系数由0.9调整为0.8之后,民航相对于高铁的边际时间节省成本产生了一个很大幅度的下降,月均收入为8 000元的消费者群体与月均收入为12 000元的消费者群体的旅行时间价值都与调整后的VOT产生了交点,且交点所反映出的里程临界点在两个消费者群体中并没有很大的差别。细分进行分析可知,对于月收入为8 000元左右的消费者,当出行的里程数超过550 km时,选择飞机出行所获得的效用大于选择高铁;对于月收入为12 000元左右的消费者来说,其出行的时间价值几乎都位于MTSC之上,即对于这部分消费者来说,选择民航出行是最优的选择。通过调整折扣后的MTSC位置变动可以看出,航空公司的降价策略可以使更多的消费者选择民航出行,从而获得一定的竞争力。但对于月收入水平低于发达地区人均月收入水平的群体来说,如月收入为5 000元左右的旅客来说(该月收入水平为经济不算发达地区的普通收入水平,其时间价值约为29.8元/h,对于这一更广大的消费者群体来说,折扣调整后,只有当出行距离达到1 550 km之后,选择飞机作为出行方式才能使总的出行效用最大化。 情景4:运行速度对旅客出行决策的影响。在与高铁的竞争中,民航的主要优势在于运行速度,而面对高铁的多次提速,民航的市场份额不断受到威胁,现对民航的平均运行速度进行调整,假设民航通过一些技术进步及飞机飞行前后准备工作效率的提高,使飞机运行的平均航行速度提高了7%,即由之前的680 km/h提高到730 km/h,则经过调整后的MTSC的计算公式变为 (28) 则调整后的MTSC与旅客出行的VOT之间的变化关系如图5所示。 图5 速度调整后的MTSC与VOTFig.5 MTSC and time value after the adjustment of speed 可以看出调整后的MTSC与调整前的MTSC几乎趋于重合,即较小幅度的速度的提高并不能从根本上改变消费者的选择,除非由于技术进行,使运营速度有了较大幅度的提高,否则单凭这一方面的微小改进,很难改变高铁与民航竞争的根本格局。 由于不同出行旅客群体的出行方式、高铁站与机场的位置、城市交通的便捷性都不相同,不同线路高铁与民航衔接时间的Δt存在一定差异;且航空公司对于机票的折扣价格也没有固定的标准,折扣的高低受到订票时间、淡季旺季、航线类型、航空公司竞争性等多方面因素的影响;且随着出行旅途里程的增加,民航的平均速度应该有所增加,而高铁由于随着里程的增加,停靠站点也会增加,高铁的平均速度可能会有所降低。所有这些计算所考虑到的因素都存在一定的不确定性,对MTSC的准确性造成了影响,且本文所考虑的旅客的时间价值为了方便直观的与旅客的边际时间节省成本进行比较,仅用收入法进行了计算,并没有考虑旅客的出行目的、出行的舒适度等对旅客时间价值的影响。因此2.3节中所得到的结果可能会与实际生活中存在一定的误差,但以下结论具有普适性: (1)高铁在短途旅行中比民航更具有竞争优势,且在一定的旅途范围内,高铁无论在价格还是时间的花费上都优于民航。 (2)在中长途旅行中,随着旅行里程的增加,民航的竞争力逐渐升高,且收入越高的旅客,越是最先开始把民航作为最优的出行方式,随着里程的增加,不同收入阶层的旅客会逐渐被吸纳到选择民航出行的群体中来。 (3)在长途出行中,民航比高铁更具有竞争优势,尤其是对于中等收入以上的旅客群体来说,当航空公司推出适当的折扣时,也会吸引一些中等收入以下的消费者选择民航出行,吸引的力度与折扣力度有非常直接的关系。 (4)提高机票的折扣力度是当前所有影响民航竞争力的因素中,最有效的解决办法,但考虑到各航空公司的盈利能力,需各航空公司根据自身成本与收入水平进行调整。 (5)由于不同区域的人均收入水平不同,因此在等距离里程的不同线路中,可能会由于消费者时间价值的差异而造成完全不同的竞争结果。2 实验验证
2.1 边际时间节省成本模型参数设定




2.2 边际时间节省成本模型参数计算
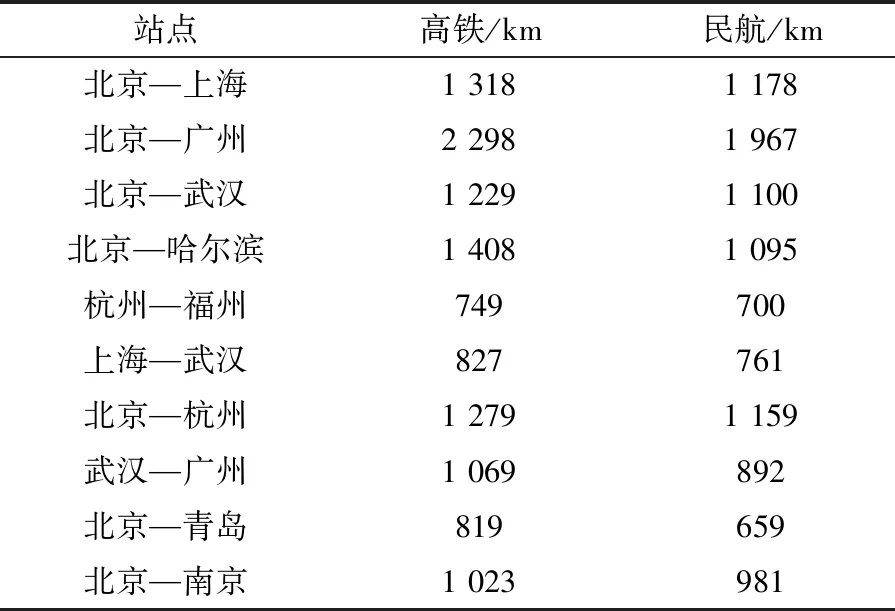

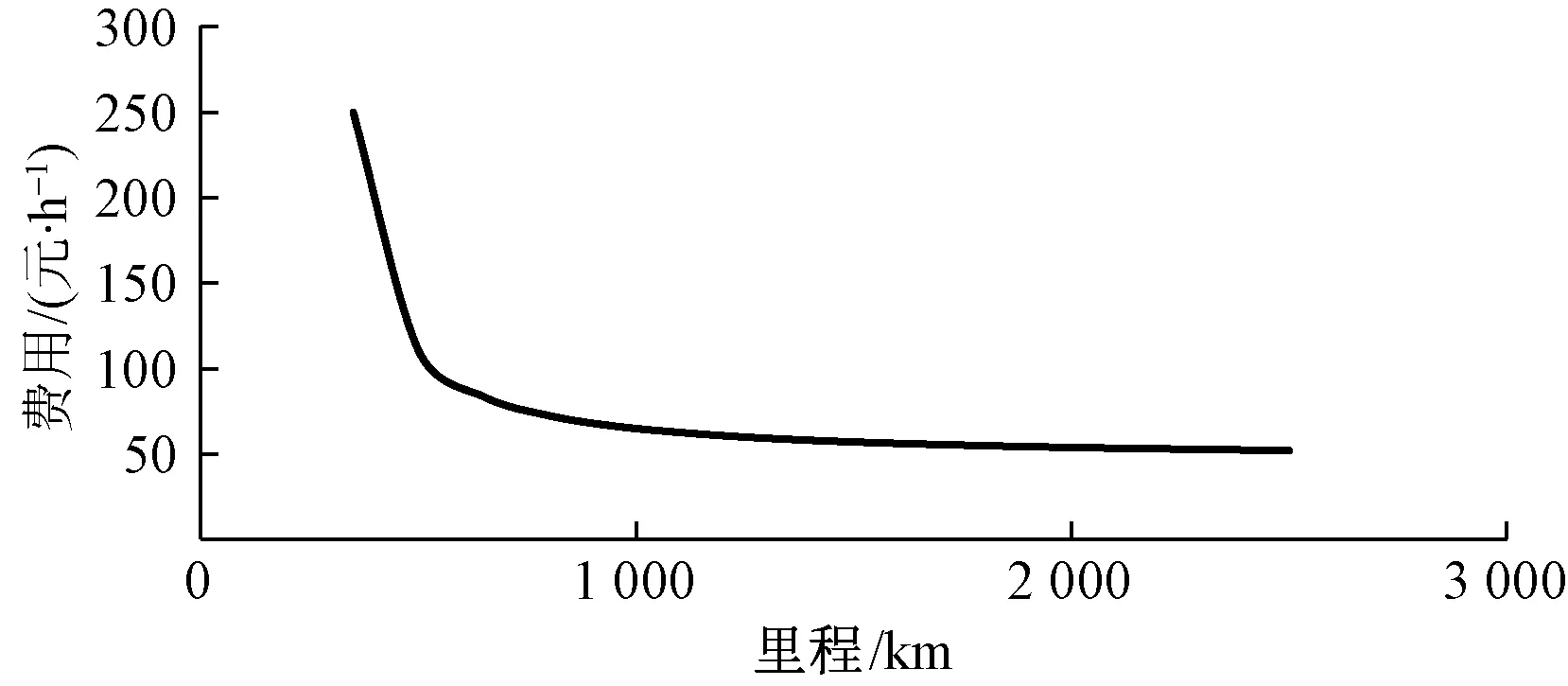
2.3 基于时间价值的高铁与民航竞争距离

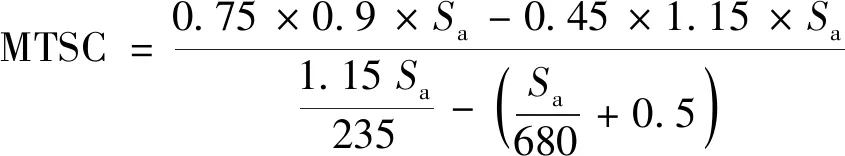

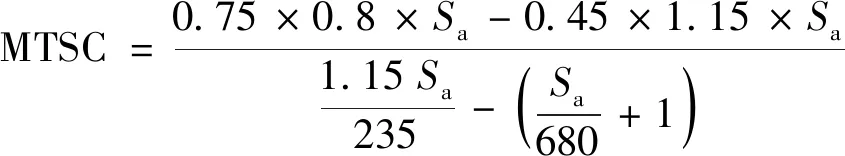
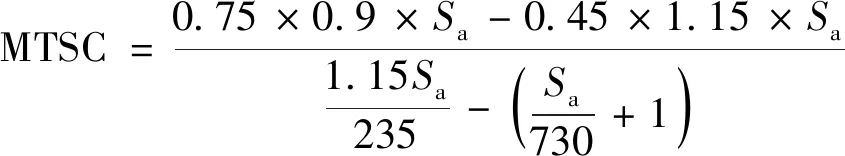

3 结论

