基于高阶谱和Tamura纹理的滚动轴承故障诊断
陆翔宇,周凤星,严保康,路鹏程,阳震
(武汉科技大学信息科学与工程学院,武汉 430081)
滚动轴承是旋转机械设备的关键零部件之一。许多机械设备发生故障都与轴承有关,轴承出现故障将导致设备产生异常的振动和噪声,轻则影响生产,重则会造成设备损伤和人员伤亡。因此,对滚动轴承在线监测和故障诊断具有重要的意义[1]。
随着滚动轴承故障方面的深入研究,目前中外对滚动轴承的故障诊断通常将信号特征提取和模式识别相结合[2]。Zhi等[3]提出了双树复小波变换和自回归(autoregressive,AR)光谱相结合的方法提取滚动轴承信号特征。杜小磊等[4]利用形态学经验小波变换和改进分形网络相结合的方法来进行了特征提取。李中等[5]利用双分支卷积神经网络实现了对滚动轴承故障位置的识别。金江涛等[6]利用变分模态分解和能量熵结合构建多模态特征矩阵,通过灰狼算法优化支持向量机有效识别轴承故障。
滚动轴承振动信号具有非线性、频谱成分多样性和二次相位耦合的特点。其在运行过程中振动信号包含大量噪声,信号特征难以提取。高阶谱对有色噪声不敏感,能有效抑制有色噪声,提取信号冲击[7]。轴承不同故障信号的冲击不同,高阶谱的二次相位耦合点也不同。鉴于此,利用高阶谱对滚动轴承正常、内圈故障、滚动体故障和外圈故障时的振动信号进行处理,得到不同故障情况下振动信号的二维等高线图。对得到的二维等高线图利用Tamura纹理完成特征提取,再将特征量输入支持向量机(support vector machines,SVM)模型以实现滚动轴承故障更精确的诊断。
1 基于高阶谱和Tamura纹理特征的滚动轴承故障识别方法
1.1 高阶谱理论
高阶谱是一种有效提取信号中非线性相位耦合的分析工具,能有效抑制振动信号中的高斯噪声,在轴承故障振动特征提取方面有着显著的优势。高阶谱也称为多谱,即多个频率的能量谱分布,是高阶矩谱和高阶累计量谱的简称。由于高阶矩存在抑制加性噪声差、没有半不变性的缺陷,因此高阶矩谱很少使用,常将高阶累计量谱简称高阶谱[8]。
高阶谱实现步骤如下。
步骤1计算其联合特征函数,计算公式为
ψ(ω1,ω2,…,ωk)=lnφ(ω1,…,ωk)
=lnE[ej(ω1x1+ω2x2+…+ωkxk)]

ej(ω1x1+ω2x2+…+ωkxk)dx1dx2…dxk
(1)
式(1)中:ψ(ω1,ω2,…,ωk)为k个随机变量x1,x2,…,xk的第二联合特征函数;φ(ω1,ω2,…,ωk)为第一联合特征函数;f(x1,x2,…,xk)为概率密度函数;E[ej(ω1x1+ω2x2+…+ωkxk)]为数学期望。
步骤2计算其k阶联合累积量,计算公式为
cum(x1,x2,…,xk)=

(2)
式(2)中:cum(x1,x2,…,xk)为第二联合特征函数的k阶偏导在原点频率ω1=ω2=…=ωk=0的值。
当x1=x(n),x2=x(n+m1),…,xk=x(n+mk-1)时,其k阶联合累积量变换为
ckx(m1,m2,…,mk-1)=cum[x(n),x(n+m1),…,x(n+mk-1)]
(3)
式(3)中:ckx(m1,m2,…,mk-1)为随机信号x(n)的k阶累积量;mk-1为时延。
步骤3得到k阶累积量谱公式为
m2,…,mk-1)e-j(ω1m1+ω2m2+…+ωk-1mk-1)
(4)
当k=3时,三阶谱被称为双谱;当k=4时,四阶谱被称为三谱。在高阶谱中双谱不仅阶数低,计算简便,而且能包含高阶谱所有的特征,故采用双谱处理滚动轴承故障振动信号,得到不同故障情况下振动信号的二维等高线图[9]。
双谱处理信号的公式为
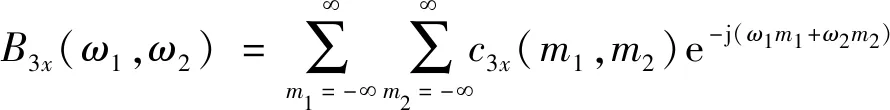
(5)
式(5)中:c3x(m1,m2)为随机信号x(n)的3阶累积量。
1.2 Tamura纹理特征理论
Tamura纹理特征包含粗糙度、对比度、方向度、粒度、规整度和粗略度6个属性[10]。
赵伟等[11]通过对图象提取Tamura纹理特征结合Copy-Move型篡改区域的检测和定位算法对图象被篡改区域进行检测与定位。白雪冰等[12]利用Gabor滤波和Tamura纹理特征对板材进行分类。
Tamura纹理的6个特征定义如下。
1.2.1 粗糙度的定义
粗糙度表示图像纹理模式的粒度大小,图像纹理模式粒度越大表示该纹理图像越粗糙,反之则越细。
粗糙度的计算方法如下。
(1)求取图像每个像元的平均灰度值,即
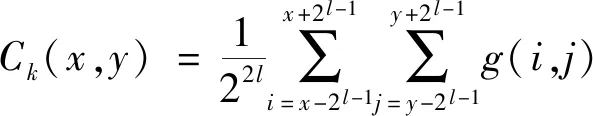
(6)
式(6)中:Ck(x,y)为该像元的平均灰度值;g(i,j)为位于(i,j)的像素灰度值;l=0,1,…,5;活动窗口大小为2l×2l像素。
(2)分别计算每个像素点在水平和垂直两个方向上未重叠窗口间的平均强度差,计算公式分别为
El,h(x,y)=|Cl(x+2l-1,y)-Cl(x-2l-1,y)|
(7)
El,v(x,y)=|Cl(x,y+2l-1)-Cl(x,y-2l-1)|
(8)
式中:Cl为位于该坐标像素点的灰度值。
(3)粗糙度计算公式为
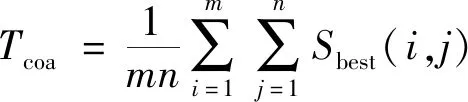
(9)
式(9)中:m和n分别为图像的长和宽;l的取值为E(x,y)=max时,设置窗口的最佳尺寸Sbest(i,j)=2l。
1.2.2 对比度的定义
指直方图明暗两部分之间的极化程度以及灰度级动态范围。可以反映图像纹理沟纹的深浅程度和图像清晰程度,沟纹越深,对比度越大,图像视觉效果越清晰,反之沟纹越浅,对比度越小,图像越模糊。
对比度计算公式为
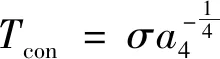
(10)
1.2.3 方向度的定义
描述纹理沿某方向集中或散布的,与纹理基元的形状和排列的规则有关。图像的形状越不规整,明暗分布范围越大,方向度越大,反之越小。
(1)将图像与式(11)的算子分别做卷积得到梯度向量在水平方向上的变化量ΔH和在垂直方向上的变化量ΔV,可表示为
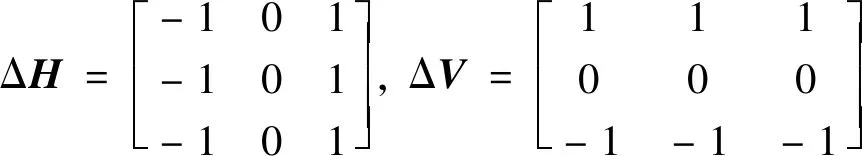
(11)
(2)计算每个像素处的梯度向量,该向量的方向角和模的计算公式分别为
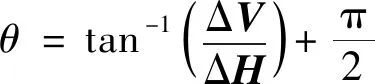
(12)
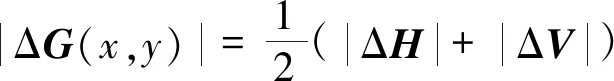
(13)
式(13)中:ΔG(x,y)为每个像素处的梯度向量。
(3)计算构造向量方向的直方图HD(l),其计算公式为

(14)
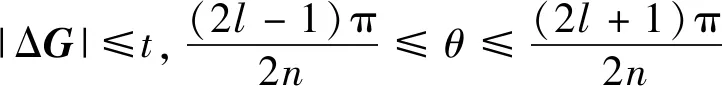
(4)方向度计算公式为

(15)
式(15)中:φ= 0,1,2,…,n-1;np为直方图峰值数目;p(p>0)为直方图HD(l)的峰值;ωp为峰值量化范围;φp为ωp中最大直方图中的量化值。
1.2.4 线性度的定义
指局部共生矩阵计算时像素间隔距离的偏差程度。图像中像素点之间隔越大其线性度越大,反之越小。
线性度计算公式为
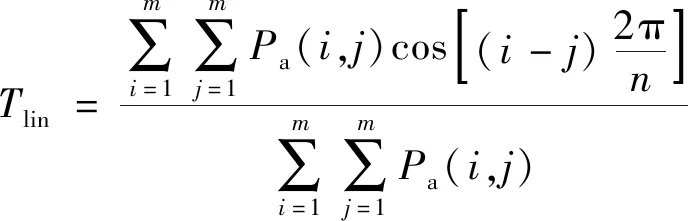
(16)
式(16)中:Pa为m×m局部方向共生矩阵的距离点。
1.2.5 规整度的定义
衡量一个图像其纹理规整的程度。图像越规整,规整度值越接近1,否则越趋近于零。
规整度计算公式为
Treg=1-r(σcoa+σcon+σdir+σlin)
(17)
式(17)中:r为归一化因子;σcoa、σcon、σdir、σlin为各纹理特征参数的标准差。
1.2.6 粗略度的定义
粗略度是心理学中用来模拟手接触物体表面的粗糙感觉。图像形状与大小不同,接触时感觉不同,图像越密集、不规则,则粗略度越大,否则越小。
粗略度计算公式为
Trou=Tcoa+Tcon
(18)
1.3 基于高阶谱和Tamura纹理特征的滚动轴承故障诊断流程
滚动轴承不同故障振动信号的高阶谱二维等高线图粗糙度、对比度、线粒度、规整度和粗略度不同,通过Tamura纹理对这些特征区域进行量化,然后将各区域量化后级联成一组特征向量作为故障识别的特征参数。鉴于此,提出一种基于高阶谱结合Tamura纹理的轴承故障诊断方法,其流程图如图1所示。首先,利用高阶谱对滚动轴承振动信号进行分析得到二维等高线图;接着通过Tamura纹理特征方法提取高阶谱二维等高线图的纹理特征参数;最后将得到的特征参数导入SVM进行故障诊断。
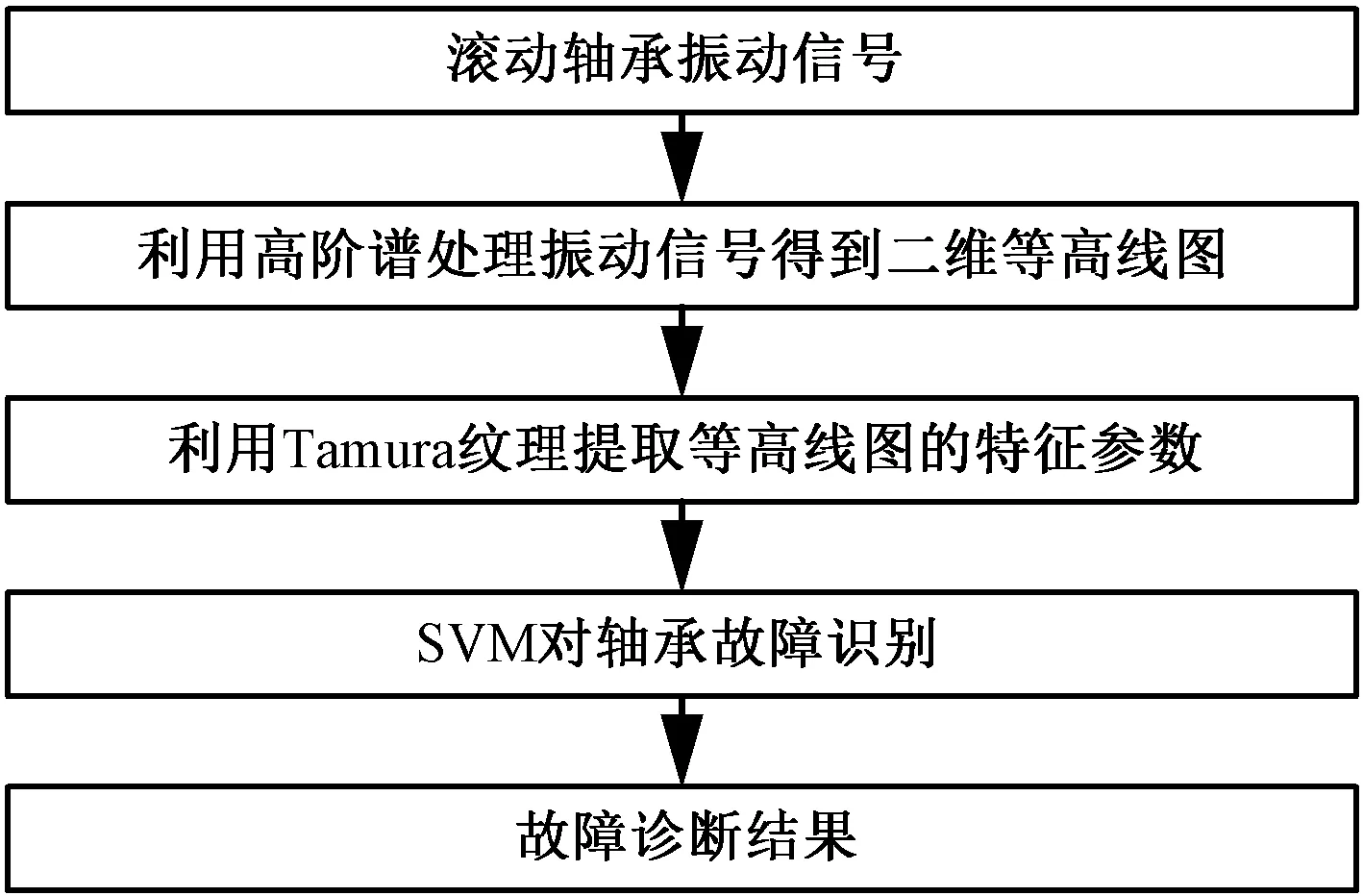
图1 滚动轴承故障诊断流程图Fig.1 Rolling bearing fault diagnosis flowchart
2 实验结果与分析
实验的数据采用美国凯斯西储大学轴承数据中心发布的轴承故障信号,其实验平台如图2所示。实验轴承型号为6203-2RS JEM SKF深沟球驱动端轴承,电机载荷为0,电机近似转速为1 797 r/min,采样频率为12 kHz,数据长度为2 048个点,实验样本集如表1所示。

图2 故障诊断实验平台Fig.2 Fault diagnosis experiment platform

表1 实验样本集Table 1 Experimental sample set
2.1 故障尺寸相同时的实验结果对比分析
选取轴承故障直径均为0.177 8 mm时的4种滚动轴承振动数据对比分析。以滚动轴承正常、内圈故障、滚动体故障、外圈故障4种振动数据的第一组数据为例,其原始振动信号如图3所示。
对图3所示的4种不同滚动轴承振动信号进行高阶谱分析得到二维等高线图,4种振动信号的二维等高线图如图4所示。
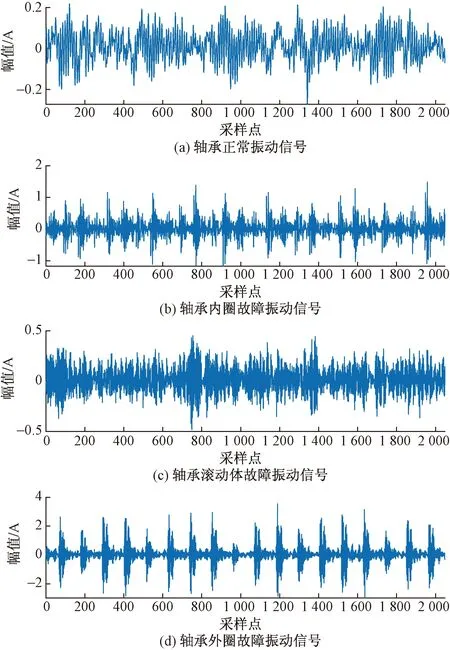
图3 滚动轴承振动信号Fig.3 Rolling bearing vibration signal
从图4的二维等高线图可以看出,滚动轴承正常时其频率呈现规则且向圆环聚拢的频率;滚动轴承内圈故障时其频率出现发散且呈现不规则的聚拢;滚动轴承滚动体故障时呈现半圆形聚拢且聚拢范围扩大;外圈故障时其频率已经在整个平面上聚拢,聚拢的形状也与其他3种状况下不同。

图4 振动信号二维等高线图Fig.4 Vibration signal two-dimensional contour map
通过Tamura纹理特征方法提取滚动轴承不同振动信号二维等高线图的粗糙度、对比度、方向度、线粒度和粗略度5个纹理特征参数,原始数据部分特征值如表2所示。
通过对表2特征参数对比分析,正常信号的粗糙度、对比度、方向度和粗略度远远低于3种故障信号的粗糙度、对比度和粗略度,可以用来区分正常信号与故障信号。故障1的对比度要高于故障2和故障3。故障2的粗略度低于其他振动信号。

表2 部分原始数据纹理特征参数Table 2 Part of the original data texture feature parameters
将本文方法与原始信号波形图提取Tamura的方法对比分析,选取有不同个数特征参数时的准确率如表3所示。
通过对表3对比分析可知,当选取两个纹理特征参数时本文方法的故障识别准确率已经达到了90%,有较高的精度,且准确率远高于原始数据提取方法的77.5%。而对比方法需要至少4个特征参数才能达到较高的准确率,本文方法相对于对比方法需要更少的特征参数,程序运行时间提升4.65%。
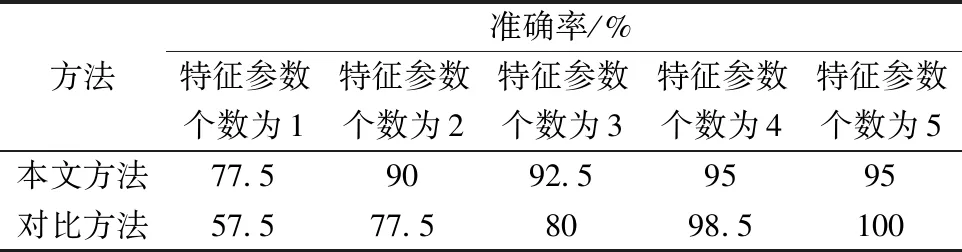
表3 特征向量个数不同时的准确率Table 3 Accuracy when the number of feature vectors is different
2.2 故障尺寸不同时的实验结果对比分析
选取滚动轴承轴承故障直径为0.177 8 mm时滚动轴承正常、内圈故障、外圈故障3种振动数据和滚动轴承轴承故障直径为0.177 8、0.355 6 mm时的滚动体故障振动数据,将本文方法与原始信号波形图提取Tamura纹理特征方法对比分析得到准确率如表4所示。
对比表3滚动轴承故障尺寸相同和表4滚动轴承故障尺寸不同时故障识别准确率,用表4中的准确率依次减去表3中的准确率,得到的准确率波动值如表5所示。
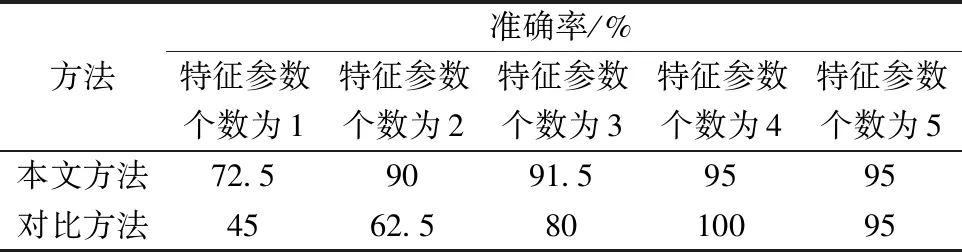
表4 不同特征向量个数时的准确率Table 4 Accuracy with different number of eigenvectors
对表5中的数据分析,当使用故障尺寸相同和故障尺寸不同的滚动轴承振动数据时本文方法识别滚动轴承故障的准确率下降范围仅有1%~5%,呈现稳定状态。而使用原始波形图提取Tamura纹理特征方法识别滚动轴承故障的准确率下降高达1.5%~15%,波动范围明显。
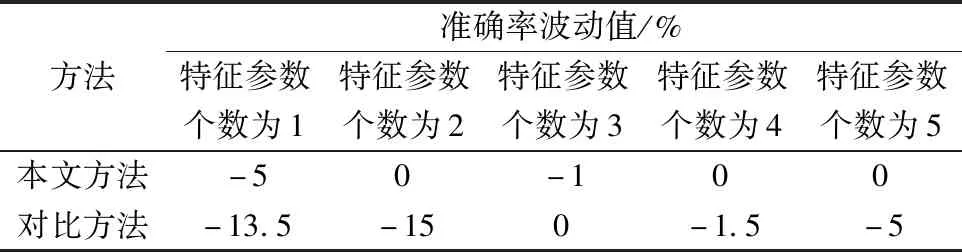
表5 故障尺寸相同和不同时准确率波动值Table 5 Accuracy fluctuation value when the fault size is the same and different
通过本文方法与对比方法准确率波动范围比较,本文方法在对故障尺寸相同或不同时识别准确率稳定率高、波动范围小。而对比方法对故障尺寸相同或不同时识别准确率稳定率低、波动范围大,所以本文方法在实际应用过程中更为可靠。
3 结论
针对滚动轴承故障诊断本文提出了一种基于高阶谱和Tamura纹理特征相结合的方法。通过实验分析得到以下结论。
(1)本文方法可以通过较少的纹理特征参数达到较高的准确率。
(2)本文方法针对故障尺寸相同和不同时识别准确率有很高的稳定性。而对比方法稳定性差,对于混合故障准确率不稳定且下降明显。
(3)本文的不足之处在于,当参数较多时准确率提升效果不是很明显。

