蒙授数学课堂教学中学生问题解决能力的培养研究

乌兰其其格

（巴彦淖尔市乌拉特前旗蒙古族中学 内蒙古巴彦淖尔 014400）

一、蒙授数学课堂教学中学生问题解决能力的培养

1.培养数学认知能力是提升数学问题解决能力的基础。

数学教学的目的是使学生能解决问题。学生的数学学习主要体现在发现问题、提出问题和解决问题的过程之中。因此，对学生发现问题、提出问题与解决问题能力的培养实际上就是对数学学习过程及其策略与方法的培养。在数学教育中，锻炼学生的数学思维是数学学科不可缺少的任务，就像我们人体需要锻炼一样，我们的思维也需要锻炼。因此，如何培养学生在数学学习过程中发现问题、提出问题、解决问题的能力，成了有必要研究的问题[1]。

实际教学中，问题解决能力的培养可以采取以下方式：

①鼓励主动质疑。教师要鼓励学生在课堂上主动提问，培养学生的内在动机，使学生质疑。②提供难度适当的问题。问题过难，不容易为学生理解，反过来，过于容易起不到应有的作用。因此，教师提出的问题要符合学生的“最近发展区”。③帮助学生正确表征问题。教师要提示学生用所学知识理解问题，或者通过画草图、列表、写方程式等方式来表征整个问题。④帮助学生养成分析问题的习惯。教师要帮助学生发展系统思考问题的方式，养成系统分析的习惯。

2.合作交流是培养问题解决能力的有效方法

有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学生学习数学的重要方式。因此，本研究特别注重了学生的“合作交流”，这无疑有助于学生的数学思维能力和问题解决能力的培养。

本研究针对的是以蒙授学校初一年级为实验班而展开的。我们通过大量进班听课观摩青亮老师的课，发现她的课基本上按“新课标”的要求注重培养了学生通过自主学习、探讨实践到合作交流的能力。具体有以下几点：①学习内容呈现出活泼生动，形式多样，有利于学生“合作交流”。②开展学生主动地观察、实践、探讨的数学活动。③课堂教学形式多样，根据不同的内容采取不同的教学方式，始终保持课堂教学中学生学习的主动性、思维的活跃性、探究实践性。研究过程中，我们发现，蒙授课堂教学中展开数学活动可以达到“新课标”要求下的良好的效果。因为蒙授学校班容量普遍适中，这为师生开展“新课标”要求下的数学活动提供了有利条件，具体表现内有以下几点：

①学生被老师关注的概率高。

②回答问题轮回次数多。

③学生在课堂上集中注意力的强度高。

④展开讨论合作交流的效果好。

⑤老师组织开展一些数学活动容易实现。

上面（图1）、（图2）、（图3）是青亮老师的一节以合作交流学习方式为主的课堂教学片段。（图1）是青亮老师在课上解答学生质疑的问题，（图2）是青亮老师提出问题请学生回答，（图3）是课堂上老师给出一定时间让学生进行合作交流的学习。

（图1）

（图2）

（图3）

3.综合学习是培养数学问题解决能力的重要方式。

综合学习是“问题解决”和课题学习的进一步体现，它是通过学生综合数学知识或者数学知识与其他知识的综合来解决一个研究课题。

数学是人类思维的结晶，它具有高度的抽象性和严密的逻辑性，学习数学需要通过思维去把握、去理解。作为教师，有责任、有义务培养学生把握数学思维的方法和思维能力。思维能力的培养，最重要的一点是改变习惯了的思维定式，从多方位、多角度，即从新的思维角度去思考问题，以求得问题的解决。

二、个案分析

（1）教学过程举例

“一元一次不等式组”教学过程举例如下：

教师：一元一次不等式的计算步骤是什么样的？

（叫学生回答）

（做了一个有关练习）（复习强化）

教师：三角形边的关系定理是什么样的？

（叫学生回答）

教师在投影仪上给出一道题让学生完成：有两根木棒长为a、b，分别是10cm、3cm。如找一根木棒做成三角形，那么c要满足什么条件？

学生：c＞10-3

C＜10+3

老师：这样联起来的两个不等式叫不等式组。

（引出本课新内容，循序渐进符合学生思维发展特点）

老师：怎么计算不等式组呢？

（举例讲解了本节课主要内容）

老师：（投影仪上）给出练习题，学生自主完成。

老师：让学生在数轴上表示结果，画出重叠的部分，写出公共部分。

老师：叫学生上黑板做练习题。（强化练习）

（老师对学生的结果给予评价，修改错误。）

老师：再强化练习。（学生自主完成，发现问题并及时改正）

老师：课后练习、作业。（培养问题解决能力必须完成的思维训练）

（2）教科书综合学习内容举例

教科书“实验与研究”“三角形边与角之间的不等关系”内容如下：

学习了等腰三角形，我们知道：在一个三角形中，等边所对的角相等；反过来，等角所对的边相等。那么，不相等的边（或角）所对的角（或边）之间的大小关系怎样呢？大边所对的角也大吗？

如图4，在△ABC中，如果AB＞AC，那么我们可以将△ABC折叠，使边AC落在AB上，点C落在AB边上的D点，则

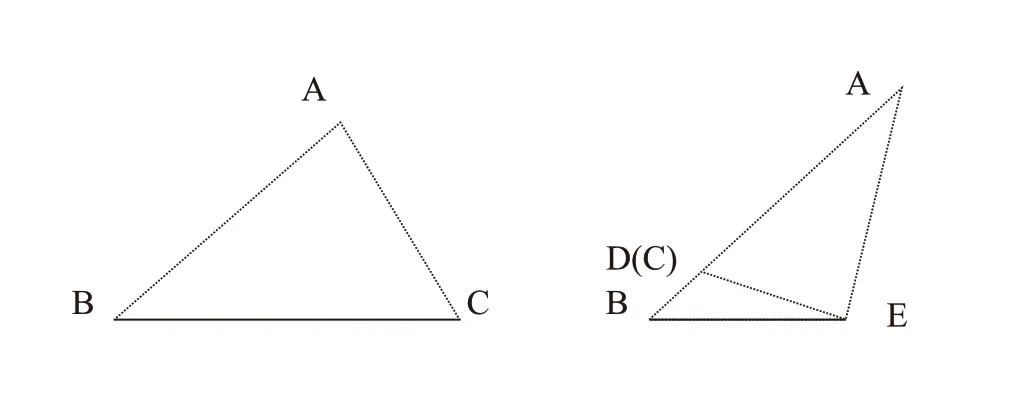
图4

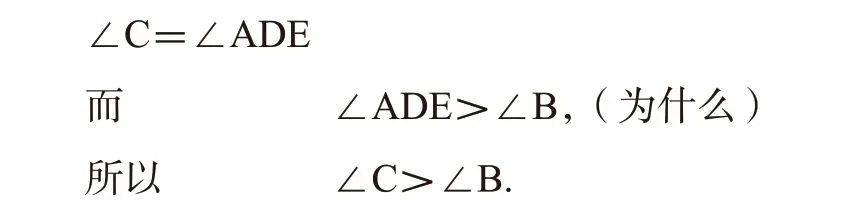
这说明，在一个三角形中，如果两条边不等，那么它们所对的角也不等，大边所对的角较大。

从上面的过程可以看出，利用轴对称的性质，可以把研究边与角之间的不等问题，转化为较大量的一部分与较小量相等的问题，这是几何中研究不等问题时的常用方法。

类似地，应用这种方法，你能说明“在一个三角形中，如果两个角不等，那么它们所对的边也不等，大角所对的边较大”吗？

利用上面两个结论，回答下面的问题：

（1）在△ABC中，已知BC＞AB＞AC，那么∠A，∠B，∠C有怎样的大小关系？

（2）如果一个三角形中最大的边所对的角是锐角，这个三角形一定是锐角三角形吗？为什么？

（3）直角三角形的哪一条边最长？为什么？”

分析：例1是青亮老师的“一元一次不等式组”课堂教学过程，这是一节典型地从认知层面上培养学生问题解决能力的课堂教学过程。例2是八年级上册教科书第十二章“实验与研究”的内容，这个内容是对前面内容有所补充的同时具有灵活性、扩展性和探索性。教师引导学生完成这类数学活动是更高一级的问题解决教学，也是情感态度与行动结合的问题解决教学模式，因此是有待进一步研究和推广的[2]。

提出问题的能力比解决问题更重要。提出问题和解决问题的要求是不同的，但两者有一个共同的关键点，那就是要能组合问题中提供的相关信息。只有认识到信息之间的联系，才能提出一个合理的数学问题。为了提高学生的问题解决能力，首先着重培养了学生的发现问题并提出问题的能力的培养。学生开始不会提问题，对这种情况，我们做了分析后发现其原因有几点：①对老师的讲解没有质疑全盘接受。②不懂收集内容中的各种信息。③对所讲内容没有兴趣。④害怕当众发言，有问题不说。⑤没有听懂。针对这种情况，教师在课堂教学应注意以下几点：①每堂课一定有一些问题提问学生。②帮助学生分析内容中的信息及关系。③能用课件的内容要用课件，简单易懂且有兴趣。④注重学习困难或胆小不发言的学生。通过这种教学方式，课堂气氛活跃了，学生的思维更灵活了。鼓励学生提出问题，实际上是在唤醒学生探索的冲动，培养学生敢于质疑。

三、总结

蒙授数学课堂教学中，提高学生问题解决能力可采取以下方式：老师提出问题（激发）—学生回答问题（反应）—学生发现问题、提出问题（质疑）—老师反应强化—学生解决问题（动手实践）。根据蒙授学校学生人数不多、班容量小的特点可采取灵活多样的数学教学活动，帮助学生提高问题解决能力；通过设置综合学习内容，培养学生应用所学数学知识解决问题的能力；专门设置综合学习时间，解决教科书中综合学习内容。

教学过程中，教学方法要围绕激发学生发现问题，提出问题，解决问题的能力，教学中设置综合学习内容，使学生能合作交流，动手实践，亲身体会学习的过程，建立一种综合学习的新模式。通过培养学生发现问题，提出问题，解决问题的能力，研究出有效的培养其数学思维能力的新模式。通过鼓励学生提出自己的观点相互讨论交流，增加学生学习数学的兴趣，进而研究出提高学生数学思维能力的新认识和新方法与策略。

学生常常因解决不了一道数学难题而苦恼叹息，数学课上回答不上来老师的提问而羞愧，如何帮助学生解决数学思维的困难是教师不断探索的问题。其实我们每个人都伴随数学成长的，数学无处不在每时每刻我们都在用数学，因此从实际出发让学生感受数学与生活息息相关的美。如，数字与生活，保龄球与三角数，人体节律与三角函数，五角星与黄金比例，圆桌会议与圆，不重复过桥等等数学与生活相连的问题都会引起学生的好奇从而激发他们解决数学问题的兴趣。

数学这门学科基础性强，前面学习的内容没有掌握好就会影响以后的学习给进一步学习带来困难，因此提高学生问题解决能力过程中提出问题让学生加以思考进行反复强化逐步使学生建立起属于自己的数学思维树。

学生问题解决能力的提升与对数学的情感态度有关系。让学生认识数学的发展史有利于培养他们对数学科目的热爱。如，让他们知道毕达哥拉斯定理即勾股定理约有500多种证明方法，是数学定理中证明方法最多的定理之一。在中国，周朝时提出勾股定理，在西方，公园前6世纪古希腊毕达哥拉斯学派提出。让学生知道我国古代记数法，希腊的符号记数法，还有零的发明，小数与对数的发明。还可以让他们知道为什么说算数是数学中的女王，圆周率π的发明及中西方对π的计算方法等等数学史的知识。将数学史知识插入课堂教学中会调动学生对数学学习的兴趣进而有助提高他们数学问题解决能力。

教无定法，要根据不同内容采取不同方法，教学的最终目标是使学生的问题解决能力得到提高。在学生的学习过程中合作交流、独立思考、教师主导、发挥学生的学习自主性无疑是因材施教的有效方法。

提高学生问题解决能力是教学的最终目标。提高学生的问题解决能力是一个漫长而艰巨的过程，本研究只是在这艰巨的任务中试着做了一个小小的尝试，目的是希望能找到一条对学生将来的发展有益的好的教学模式[3]。

四、需要继续讨论的问题

（1）培养学生问题解决能力还需将教学内容与实际生活多联系。解决各种问题需要师生有综合知识与综合学习能力。如何加强学生综合学习能力是需要进一步讨论和研究的问题。

（2）在教学过程中，应该组织小组之间、学生之间、师生之间开展积极有效的评价。让学生通过评价他人解决问题的过程，形成自己对问题的明确见解；引导学生对解决问题的过程进行回顾和反思，进而提高他们问题解决能力。

（3）学生的问题解决能力的培养不是一朝一夕的事，实验了一段时间后对效果的呈现有疑惑。因此，如何做才能有更好的效果是接下来思考的问题。

（4）综合学习内容没有列入课堂教学内容中，因此，在课堂教学中插入此类内容感到困难。“综合学习”教学方法在实施过程中与教科书的内容设置及要求有不能很好地融合之处，需要进一步研究与实践。

（5）情感态度与学习行为在问题解决中如何结合是需要进一步研究的问题。