基于AS-NSGA-Ⅱ算法的多旋转货架储位优化研究

段军雨，芮万智，贾正荣

(海军工程大学 舰船综合电力技术国防科技重点实验室，武汉 430033)

0 引言

多模块旋转货架装置以其周转速度快、占地空间小、准确率高等优点常配置于现代物流仓储系统，广泛用于种类、数量繁多货品的控制和管理。储位分配优化针对货品与货架两者的关系，使得货品存储顺序、货架仓储空间得到合理安排，实现高效入库作业，以此达到提升货架的协同作业效率、节省调度成本的目的。

储位分配优化的问题模型主要分为“网格填充式”自动化立体仓库、“回转排列式”旋转货架装置。对于自动化立体仓库的储位优化研究，分别以货品的出入库频率[1]、货架稳定性[2]、货品关联性[3]、空间利用率[4]等为优化目标，或者结合多目标[5-6]建立数学模型，取得了诸多有意义的研究成果；对于旋转货架模型采取的约束条件、优化目标较为单一，主要结合直观的启发式策略以缩短入库时间[7]、保持货架稳定性[8]等为目标，进行旋转货架储位分配模型的建立。

储位分配优化的求解算法主要是结合多目标优化模型进行改进，在不同程度上提高了原智能算法的求解效率。王贺[9]通过自适应遗传算法求解以货品关联规则、空间利用率为目标的储位分配问题；焦玉玲[10]设计了多种群遗传算法，并采取加权方法将储位优化的多目标问题转化为单目标进行求解；蔺一帅[11]建立了以缩短作业时间、提升货品相关度为目标的储位优化模型，并结合改进的协同优化遗传算法求解；印美[12]采取基于NSGA-Ⅱ和动态仓储模式的优化方法，求解能耗、货架稳定性、作业效率3个目标的储位优化问题；朱杰[13]通过线性加权建立储位优化的多目标模型，提出改进的自适应遗传模拟退火算法求解；薛亚莉[14]提出一种基于遗传模拟退火的Memetic算法求解货位分配模型。

分析上述文献可知，一方面，多目标储位优化主要以立体仓库为问题模型，而对于旋转货架模型的存储策略及优化目标单一，现有的多模块、多目标储位优化模型不能够适用于旋转货架装置的研究；另一方面，用于求解多目标优化问题的遗传算法不断深入推广，改善了算法的求解性能，但以往仅基于遗传算子或者进化阶段融入改进策略，即单方面考虑进化环境对个体或者种群的影响，仍存在一定的局限性。因此，本文建立包含作业能耗、装置稳定性以及存储效率目标的多旋转货架储位优化模型，提出一种基于自适应策略的非支配排序遗传算法(NSGA-ⅡBased on Adaptive Strategy, AS-NSGA-Ⅱ)用于求解多旋转货架装置的最佳储位分配方案，并通过仿真试验对比说明算法具备更优的计算性能。

1 多旋转货架储位优化问题描述

多旋转货架装置由N个旋转货架组合而成、并列摆放，允许混装各类货品，沿正、反方向任意转动。各个货架包含的储位大小相同、数量M不同(M={M1,…,My},y≤N)，货品规格根据对应的货品种类确定，其中货品规格是指存储货品占用的空间大小。多个出入库堆垛机与各个货架一一对应，货架匀速转动且按照货品类别依次完成入库，直至得到所有货品的储位分配结果。“回转排列式”多旋转货架装置如图1所示。

图1 多模块旋转货架装置示意图

结合上述多旋转货架的存储布局方式，将储位优化问题的调度原则总结为四项，具体内容如下：

1)分散存储原则：为避免某个货架故障或阻塞，影响调度作业的进行，使同一类型货品分散存储于各个货架，即将各类货品在多个旋转货架上“按比例分层”，以此为约束条件将问题转化为单个旋转货架的储位优化。

2)货架稳定性原则：货品分布需要保证装置的受力均匀，避免因重量失衡而影响整个货架的安全性。根据货品的平面坐标(x,y)(x表示旋转货架上的储位坐标，x≤M；y表示旋转货架编号，y≤N)以及对应的货品重量，计算货架重心使其保持均衡。

3)存储效率原则：堆垛机在顺、逆时针方向均以速度v转动，不考虑堆垛机启动、操作等准备时间，货品的入库效率能够以过程中转运时间的数学期望来描述。

4)作业能耗原则：周转率高、质量大的货品放置在离出货口近的储位上，能够减少货品出库时的运行成本，提升作业效率。考虑将储位和货品进行编号，通过编号对应得到储位-货品的耦合关系，表示储位上货品运出时的能量消耗。方式如下：

①储位编号：为产生储位排序的优先级，通过构造储位能耗算子[12]E排序各个储位，表示为：

E=l×g×c

(1)

式中，g为重力加速度、c为摩擦系数、l为储位到出入库堆垛机的水平距离。将储位能耗算子进行排序得到储位编号C，表示货品转运消耗能量的高低。

②货品编号：根据货品立方体索引规则[15]，将货品索引值(Cube-Per-Order，COI)进行修改表示货品编号：

(2)

式中，Ij为某类货品j(j=1,…,K)的COI值，Sj为货品j对应的储位空间(入库数量×货品规格)，fj为货品j的周转率，mj为货品j的重量。依据COI值将货品从小到大进行排序，体现货品的优先调取顺序。

2 多目标储位优化数学模型

结合问题特点和调度原则，考虑以货品分散存储、货架实际装载情况为约束条件，将所有货品进行“分层”操作，使得原问题转化为单个旋转货架的储位优化问题，以降低转运能耗、稳定储存重心、缩短入库时间进行多目标优化，从而构建多旋转货架储位优化的数学模型：

1)货品分散存储。

依据旋转货架数量N、储位数量M，将K类货品进行“按比例分层”，确定各个货架上分配的货品种类和数量，即得到每类货品在各个货架上分配的数量集合，数学描述为：

le(j)={|u1|,|u2|,…,|uy|}

(3)

(4)

式中，单个旋转货架上的储位总数My；货品j的库存总数Uj；uy表示货品的分层数量，|a|表示对a向上取整。

2)减少货架转运能耗。

依据根据公式(1)、(2)得到的储位编号C和货品编号Ixy，完成各类货品与储位的合理对应，即将COI值偏小的货品与能耗算子低的储位对应，达到降低转运能耗的目的，即Ixy与C的乘积最小，数学描述为：

(5)

3)提高储存重心稳定性。

考虑到旋转货架水平放置，合理分配两侧货品的重量来实现旋转货架稳定，使得旋转货架的等效重心接近水平方向的中心轴线，即旋转货架的几何重心与中心轴线的距离最短，数学描述为：

minFG(x,y)=

(6)

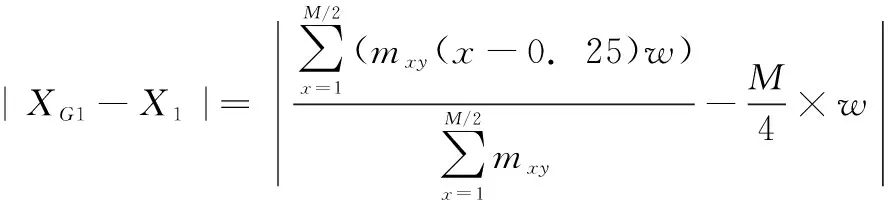
(7)

(8)

式中，w为单个储位宽度；XG1、XG2表示旋转货架等效的几何重心位置；X1、X2表示中心轴线位置；mxy表示货品重量。

4)减少货品入库时间。

为提高作业效率，旋转货架按照类别依次装载货品、规划转运路径，能够有效缩短货架转运时间，即使得周转率越高的货品入库时间越短，以货品入库时转运时间的期望值最小为目标，数学描述为

(9)

式中，fxy为旋转货架y、储位坐标x上货品的周转率；txy表示该储位货品完成入库的转运时间；

因此，多目标储位优化模型描述为：

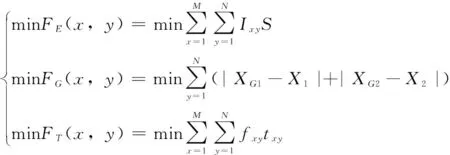
(10)

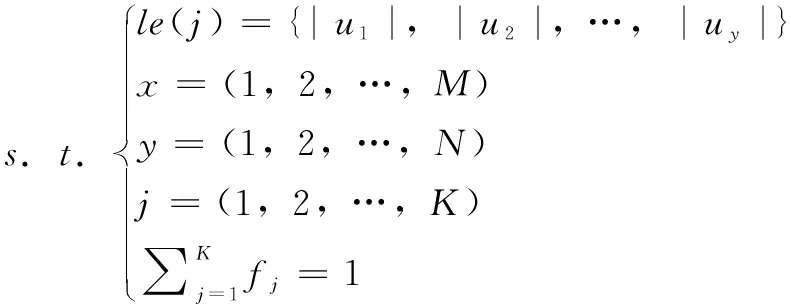
(11)

3 AS-NSGA-Ⅱ的算法实现

NSGA-Ⅱ是用结合遗传算法解决多目标优化问题的常用算法，为协调各个目标函数间的冲突关系，主要通过3种方式：精英策略选择、快速非支配排序、拥挤距离计算[16]。多旋转货架的储位优化问题属于多变量多约束问题，采取NSGA-Ⅱ求解存在后期收敛速度慢、解集多样性不理想的现象，适应性策略能够抑制该现象的发生。然而原始适应策略通常以进化环境和种群进行分类[17]，未结合两者考虑使其存在局限性，自适应策略在此基础上进行改进，实现进化环境、种群以及非支配分层等级对遗传算子的改善。

AS-NSGA-Ⅱ的设计及流程：

针对原始适应策略与NSGA-Ⅱ的缺陷，AS-NSGA-Ⅱ通过引入自适应策略，即设计选择操作方式，交叉算子、变异算子的动态调整模型，提升原算法的全局寻优性能。为便于阐述算法步骤，对涉及的参数进行定义如表1所示。

表1 算法参数定义

1)编码、解码方式。

初始种群的染色体编码采用实数编码方式，为便于计算将环形货架进行线性展开，依据储位排列方式得到编码X。取m个互不重复的随机整数组成一个染色体(取值范围[1,M])，即表示进化过程中的一种储位分配方式，染色体中的每个基因元素表示相应的储位位置，形如：

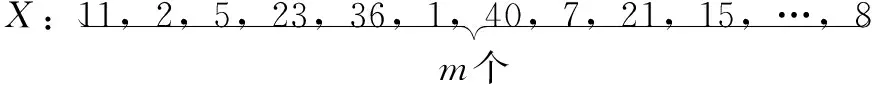
解码时根据货品类别以及入库数量，将染色体编码进行分区，每个元素值在划分后得到对应的分区类别则作为解码值Y，当类别k∈[1,3]时，染色体的编码、解码表示为：

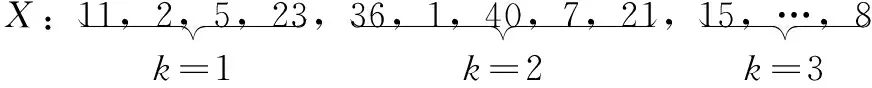
Y:1,1,1,1,2,2,2,2,2,3,…,3

由解码值组成的整数序列对应染色体编码中的基因元素，即为各类别货品分配的储位位置，所有染色体的编码、解码值组成规模为N×m的数组表示货品的储位分配方案。

2)选择操作设计。

NSGA-Ⅱ算法常使用二元制锦标赛进行选择和精英保留，该方式在进化前期选择父代个体通常发生局部收敛现象，不能保证解集的多样性。为此，本文结合自适应策略能够动态调整目标函数值，采用轮盘赌法进行并列选择父代个体，提升算法收敛速度并保证解集空间分布均匀。

其中，并列选择是在执行选择操作之前，将染色体种群划分成多个子种群，种群数量同目标函数数量，使得子种群与目标函数一一对应。根据目标函数适应度计算概率，通过轮盘赌法在各个子种群中并列进行、按概率选择，最后合并成新的染色体选择种群。

sigmoid曲线函数[14]能够平衡线性和非线性之间的取值，自适应选择方式基于sigmoid函数进行改进，根据迭代次数、非支配分层等级调整个体的目标函数适应度，表示为：

(12)

因此，在每代进行轮盘赌选择时，依据自适应策略得到个体的选择概率为:

3)交叉操作设计。

排列优化问题中的染色体基因元素通常只出现一次，若保持NSGA-Ⅱ常用的模拟二进制交叉，会使得染色体中的基因元素排列紊乱。针对研究的储位优化实数编码方式，本文采用部分映射交叉算子(PMX)进行交叉，即个体间部分基因元素进行互换，通过映射操作保证染色体无重复、排列合理，如图2所示。

图2 交叉操作

为提升算法整体的搜索速度，抑制种群陷入局部最优解，一方面交叉操作基于进化环境(进化阶段、非支配分层等级)交叉率实现自适应调整，并且为保留每代种群中的较优个体，将交叉算子调整模型分为两种，表示如下：支配个体交叉率：

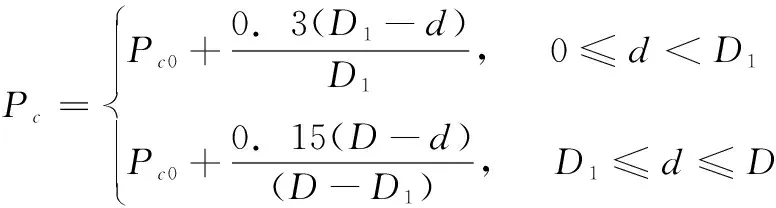
(13)

非支配个体交叉率：

(14)

另一方面，为提高种群的环境适应性，动态调整随机选择的交叉映射区域，并且合理设置α(α∈(0,2])保证操作的基因个数为非零渐近值，本文设置为1.5，表示为:

(15)

4)变异操作设计。

针对旋转货架的储位分配特点，变异操作采用基因位对调方式，并设定个体变异时选择解码值不同的基因位对调，避免同类货品储位间的循环变异。为提升精英个体(适应度高的个体)的选中概率，结合自适应策略调整变异率、区域。变异算子的调整模型表示如下：

支配个体变异率：

(16)

非支配个体变异率：

(17)

基因位对调区域：

Lm=ceil(rank(i)/eα)

(18)

5)最优个体选择。

在求解j个目标的问题优化时，由于解集中目标函数的单位、量级不同，因此要通过归整处理对其进行调整，并得到个体的目标函数值适应度，表示为：

(19)

(20)

式中，β参数的取值为0.005，其设定是为了避免目标函数值出现超出阈值的计算结果。

设定适应度参考指标为(1,1,1,…,1)K，寻找近似参考指标最大的个体，确定其为Pareto最优解集中的最优个体，即H(max)=H(i)，则Pbest=P(i)。

6)算法实现。

基于AS- NSGA-Ⅱ求解多旋转货架储位优化模型的步骤如下。

输入：订单任务信息(入库任务类型、货品种类及数量)，货架编号；

输出：各个货架的货品种类、数量，储位分配结果；

Step1：初始化算法参数(pop、D、Pc、Pm)，采取实数编码、解码生成初始种群，；

Step2：对种群个体进行非支配等级划分， 计算个体的适应度值、拥挤度距离，并进行赋值更新；

Step3：根据自适应策略调整目标函数值，通过轮盘赌方式并列选择多个子种群，合并成新种群；

Step4：通过设计的交叉、变异操作得到与父代种群Pk相同规模的子代种群Ok；

Step5：父代种群Pk、子代种群Ok组成中间子群，依据其非支配排序分层等级、拥挤度距离进行排序，通过二元制锦标赛方式保留固定数量的精英个体，得到进入下一代的新种群；

Step6：判断算法是否满足最大进化次数，若满足，输出pareto最优解集、前沿，否则返回Step2；

Step7：通过目标函数归一化，从pareto最优解集中选取最优个体，得到最佳储位分配方案。

AS- NSGA-Ⅱ算法流程图如图3所示。

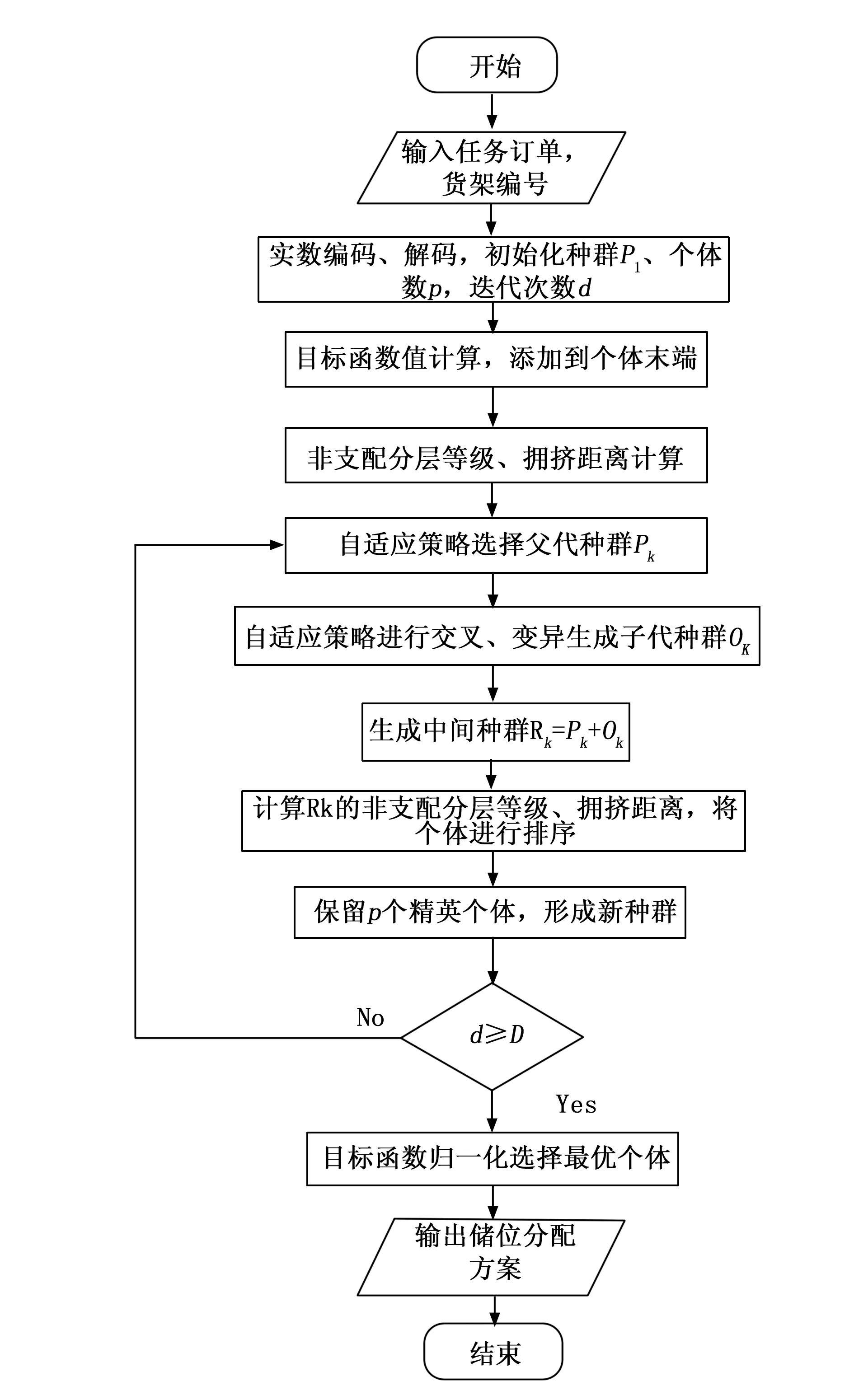
图3 储位优化求解的算法流程图

4 实验分析

4.1 算例分析

4.1.1 测试参数设置

本文以某军械仓库的一条自动化生产线为例，配置的多旋转货架装置数量为10，每个货架的储位数量在80～100之间随机选取，储位大小为1×1m2，水平转动速度为0.12 m/s。根据某次执行的入库订单任务，货品参数如表2所示，周转率表示货品入库次数占总次数的百分比，编号根据货品COI值而定。

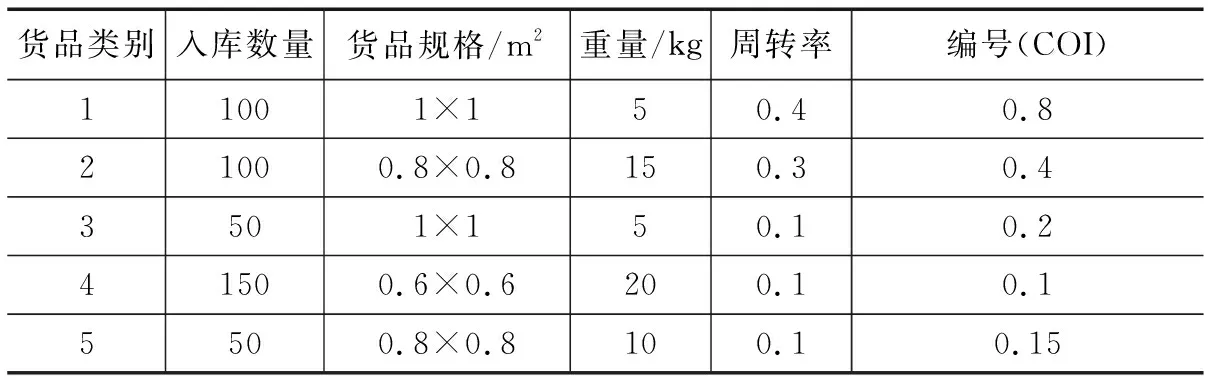
表2 入库任务货品参数

为验证本文算法的求解效果和性能优势，根据货品参数得到的“分层”结果，采用NSGA-Ⅱ、多种群遗传算法[10](MPGA)以及本文的AS-NSGA-Ⅱ对多目标储位优化进行测试。通过Matlab实现算法编程、模拟数值计算，设置种群规模p=300，最大进化次数D=500，初始交叉概率Pc0=0.5，变异概率Pm0=0.05。

4.1.2 模型验证

为验证多目标优化模型的正确性，分别以(能耗)FE、(重心差值)FG/m、(转运时间)FT/s进行优化，将求解结果与基于多目标优化的最优解进行对照分析，对比结果如表3所示。

表3 单目标、多目标优化结果对比

由表3可以看出，相比以FE最小进行的单目标优化，多目标优化结果以增加能耗指标为代价，不仅减小了重心差值，而且缩减了转运时间。同样，分别对比以FG最小、FT最小的单目标优化，多目标优化都能够降低另外两个目标函数值，由此，可得多目标优化符合Pareto最优解集思想，验证了多旋转货架储位优化模型的正确性。

4.1.3 目标函数值对比分析

根据选取的最优个体确定最佳储位分配方案，对比传统方法(顺序存储)与各算法优化后的3个目标函数值。由表4可知，较传统方法求解，NSGA-Ⅱ、MPGA、AS- NSGA-Ⅱ对于FE目标值分别降低了47.0%、46.4%、40.7%；对于FG目标值分别降低了93.53%、95.02%、94.03%；对于FT目标值分别降低了37.4%、35.8%、44.6%；在Pareto前沿中各目标函数值存在竞争，其中一个减小会引起其他两个目标函数值变化，因此，各算法对于能耗FE、转运时间FT的优化率在合理范围内，能够保证Pareto前沿质量。然而在实际仓储应用中，衡量调度作业效率的转运时间FT作为首要目标，AS- NSGA-Ⅱ的储位优化结果更符合预期。

表4 各算法优化结果

4.2 算法性能分析

4.2.1 性能分析指标

用于分析多目标优化算法的性能指标主要涵盖两部分[18]：

1)算法的时间复杂度。AS- NSGA-Ⅱ算法是对NSGA-Ⅱ算法加入自适应策略的改进，一方面通过轮盘赌方式对种群进行并行分类选择，另一方面对交叉算子、变异算子增加动态调整操作，两方面在操作步骤中并行调整且均为线性，因此两者的时间复杂度一致均为O(mn2)，其中其中m为优化目标数量、n为进化个体数量；AS- NSGA-Ⅱ算法与MPGA算法对比，MPGA算法在构建初始种群时生成多个子种群，解集在子种群间协同进化、串联进行，时间复杂度为O(lmn2)高于AS- NSGA-Ⅱ算法，其中l为种群数量。

2)评价解集的收敛性和多样性。算法在保证Pareto前沿质量，使求得Pareto最优解集尽可能接近理想最优解的同时，提升解集的收敛性和多样性。分别采取收敛性准则[19](GD,generational distance)、分布多样性准则[20](Diversity MetricΔ)评价算法的收敛性、多样性，定义如下：

(21)

(22)

其中:GD值越小，表示Pareto前沿与最优目标函数值的差距越小，代表收敛性更好；Δ值越小，Pareto前沿边界值与极端值的距离越小，连续解向量之间的距离与均值越相近，代表多样性更好。

4.2.2 结果和分析

1)算法收敛性分析。

通过图4可知，AS- NSGA-Ⅱ在进化前期不易陷入“早熟”，收敛速度比NSGA-Ⅱ、MPGA更快，并且在进化后期个体与Pareto前沿的距离更近。这是由于引入自适应的并列选择方式，提升了个体对于目标函数值的选择灵敏度。

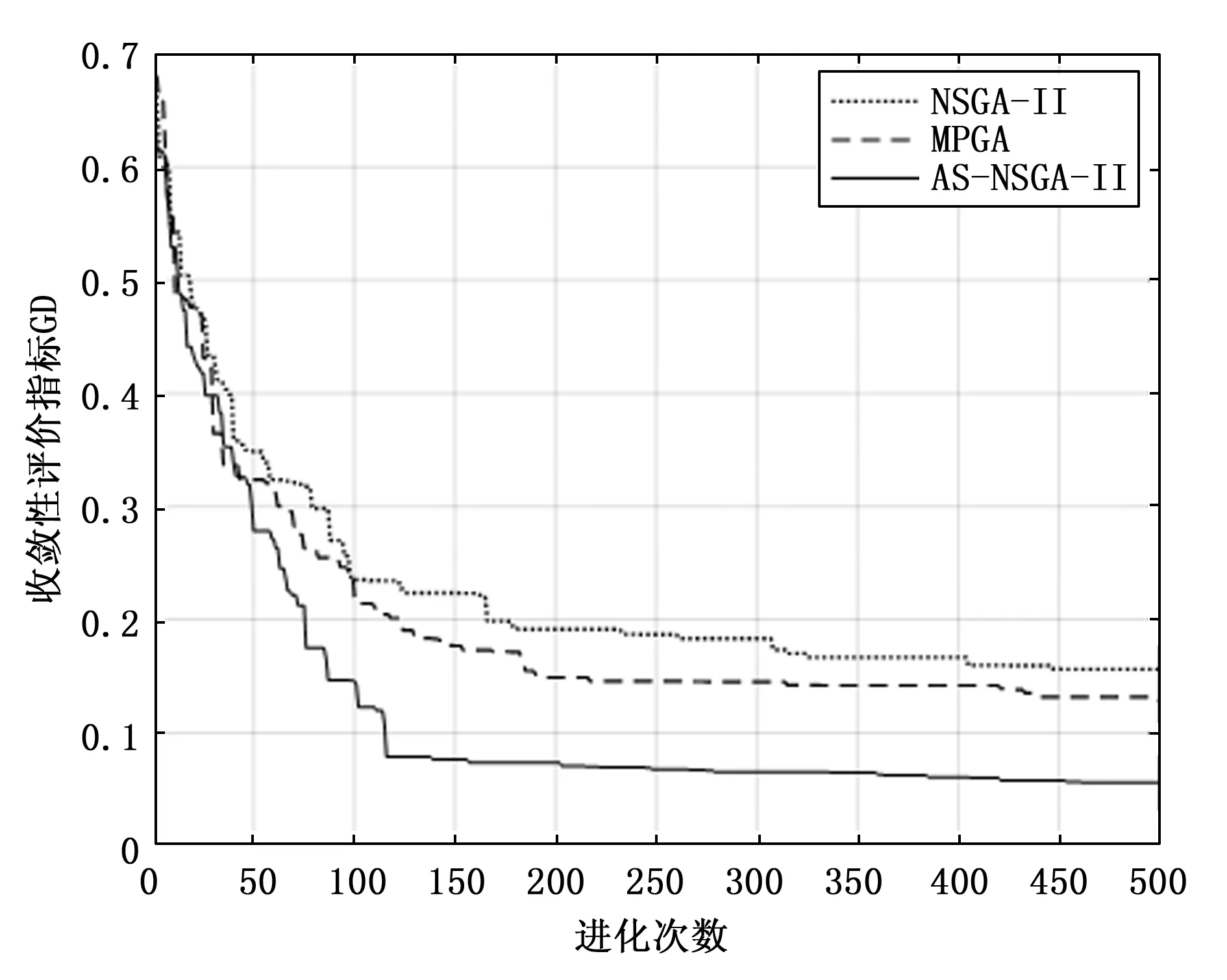
图4 收敛性测试结果

为验证各个算法的求解结果是否存在显著差异，采取3种算例输入，对每个算法进行100次重复试验，计算GD指标的均值、方差如表5所示。

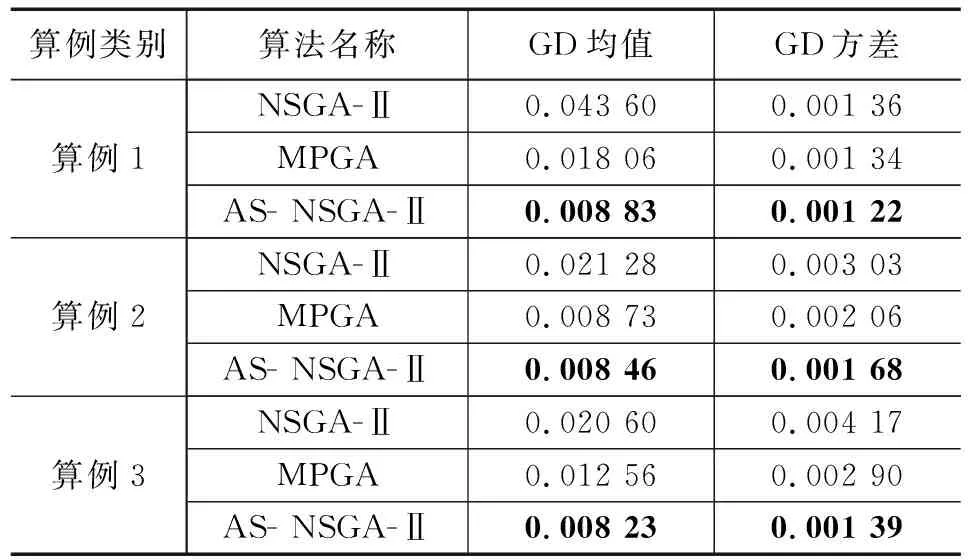
表5 收敛性评价指标分析

由表5分析可知，3种算例情况下，AS- NSGA-Ⅱ求得Pareto最优解集的收敛性能指标值更小，表现的全局收敛性更优。

2)算法多样性分析。

由图5可以看出，NSGA-Ⅱ、MPGA 求得的Pareto最优解集空间分布不均匀，而AS- NSGA-Ⅱ对应解集的空间分布性更好、更加均匀，这是由于根据进化阶段和非支配分层等级，自适应调整交叉、变异率以及交叉、变异区域，提升了种群和个体对环境的适应能力。

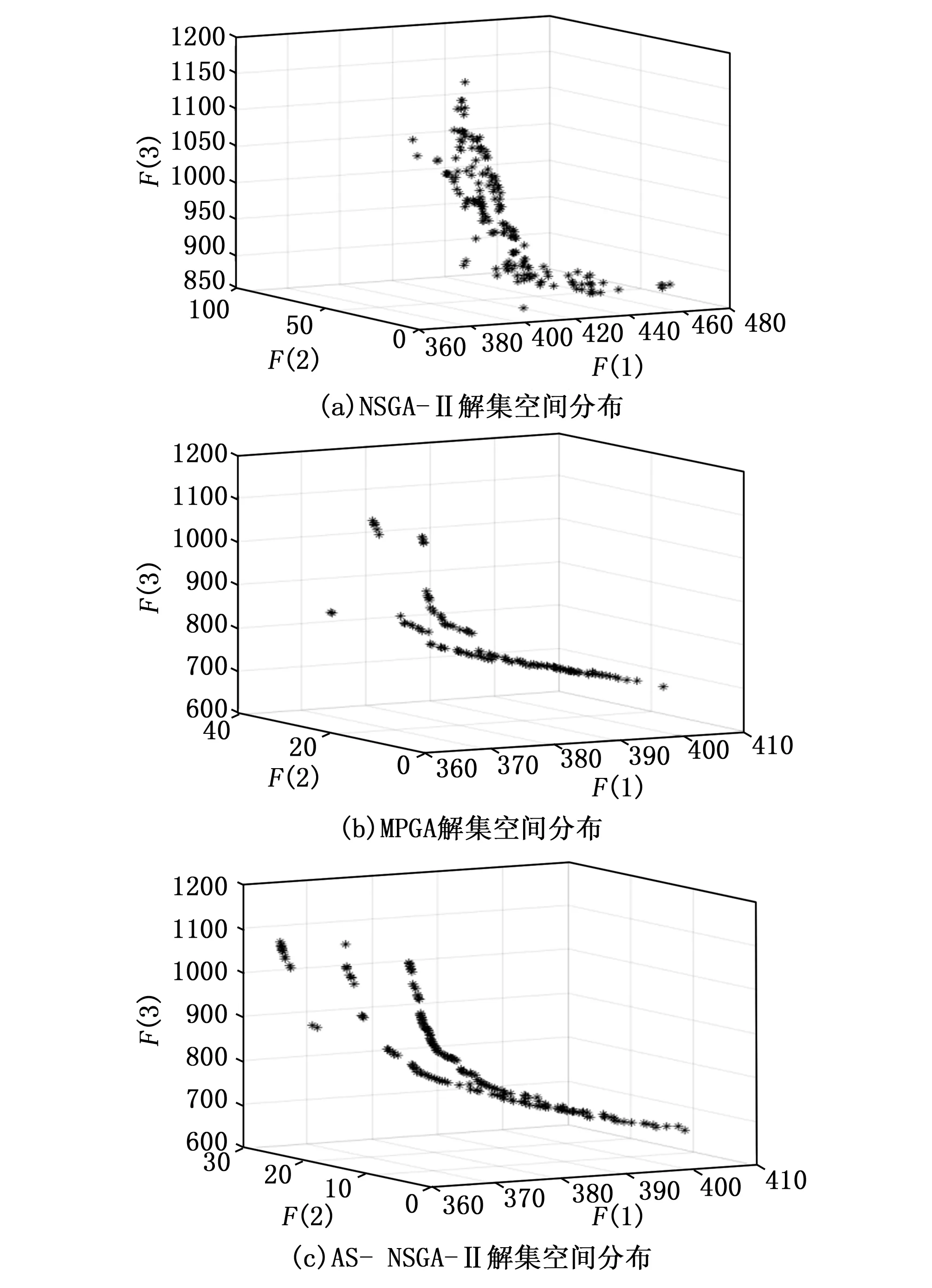
图5 算法多样性测试结果

为具体比较算法的多样性指标Δ，采取3种算例输入，同样对每个算法进行100次重复试验并计算Δ的均值和方差，如表6所示。

表6 多样性评价指标分析

由表6可知，算例3 中AS- NSGA-Ⅱ的Δ均值和方差均为最小，表现多样性更好，虽然算例1、2中AS- NSGA-Ⅱ多样性指标方差略高于其他两个算法，但其多样性指标均值为最优，提升了原算法Pareto最优解集的多样性。

5 结束语

本文结合多旋转货架的储位分配原则，以转运能耗最低、储存重心最稳、入库时间最短作为优化目标，建立旋转货架储位分配的多目标优化数学模型，并改进、设计非支配排序遗传算法，提出了一种AS- NSGA-Ⅱ算法求解储位分配模型。该算法考虑进化环境对个体或者种群的影响，结合轮盘赌法进行并列选择进化个体，通过进化环境动态调整交叉、变异率和交叉、变异范围，对Pareto前沿进行加权归一化处理得到储位分配最优方案，同时给出了自适应模型实现运行参数的调整，达到自适应进化的效果。仿真实验分析表明，AS- NSGA-Ⅱ算法具有更好的收敛性、多样性以及执行效率，对于求解多旋转货架储位优化问题具有良好的计算性能。