新冠疫情背景下央行货币政策与银行系统性风险之间的关系研究

袁金霞

（池州经济技术开发区管委会 投资促进局，安徽 池州 247000）

1 问题的提出

近年来，新冠疫情导致全球经济的大幅衰退，同时也导致了金融领域出现诸多的风险事件。面对疫情后，中国政府采取果断的措施遏制了疫情蔓延，即使如此，中国的经济也遭受了相当大的损失，据国家统计局发布的统计数据显示，2020年一季度中国的GDP同比下降6.8%，面临的经济环境更为复杂，经济发展的各个方面都受到严重的影响。防范和化解国民经济中的重大风险最主要的一条就是要保证不发生系统性风险。

从现有的文献可以看到[1-7]，国内外学者就货币政策对银行业的系统性风险的影响具有较为一致的结论，即货币政策能够抑制银行业系统性风险。在疫情背景下，中国采取多项货币政策和宏观审慎政策稳定经济，研究货币政策对银行业的系统性风险的影响，这样既能保证中国采取的货币政策的有效性，为其他国家的经济复苏提供借鉴，还能从理论上揭示在重大突发事件的影响下，货币政策对系统性风险的影响机理。

2 模型构建与数据来源

2.1 ARMA-GARCH

为了能对系统性风险进行合理的度量，采用ARMA-GARCH模型对各家银行的收益率建模，以此得到较为准确的系统性风险。模型分为两部分建模，一是对均值方程进行建模，即公式（1），二是对波动率方程进行建模，即公式（2），均值方程建模采用ARMA模型，波动率方差建模采用GARCH模型。同时假设标准化残差服从student t分布，由ARMA-GARCH模型对均值和波动率进行合理的模型构建。

2.2 系统性风险建模

在对收益率进行建模之后，利用VaR(在险价值)度量每个银行自身面临的风险，在VaR的基础上利用CoVaR（条件在险价值）来度量在单个银行出现风险时，系统性风险产生的变化。利用下面的公式（4）和（5）对单个银行的风险和系统性风险进行度量。

2.3 回归模型

为了考察货币政策与系统性风险之间的关系，选取一定的指标作为货币政策的替代变量与系统性风险建立回归模型，考察货币政策对银行业系统性风险的影响。

2.3.1 被解释变量 被解释变量为系统性风险；各个银行的系统性风险由前述模型可以计算得到，将系统性风险作为被解释变量，考察货币政策对其产生的影响。

2.3.2 核心变量 核心变量的选择主要用来对货币政策进行量化，参考王妍等（2019）和陈国进等(2020)的研究[8-9]，央行采取的货币政策大致分为以下几类：一是通过释放货币，直接通过向市场投入更多的货币以提高货币的流动性来对市场进行调节；二是对准备金的调节，央行通过对各个银行的准备金进行调节，以对流动性进行控制；三是对基准利率进行调节，通过对基准利率对市场利率进行调节；四是公开市场操作，包括正回购和逆回购。因此在选择核心变量来代替货币政策时，通过M2、金融机构存款准备金率，一年期存款基准利率、正回购和逆回购量等方面的指标来对筛选变量。

在核心变量的设置中，为了突显新冠疫情的背景，采用虚拟变量（Variable）区分新冠疫情发生前后，即新冠疫情发生前记为0，新冠疫情发生后记为1，以2020年1月作为新冠疫情发生的时间节点。

2.3.3 控制变量 方意等人（2012）的研究认为宏观经济因素在银行业系统性风险中起到较为重要的作用，参考他们的研究，在模型中为了考虑宏观因素对系统性风险的影响，将消费者价格指数（CPI）加入到模型中；消费者价格指数反映的是宏观经济中的通货膨胀水平，能够反映经济的整体状况[10]。

同时加入宏观经济景气指数（Index），以考虑宏观经济的状况对银行业系统性风险的影响。此外，为了反映经济发展过程中的就业水平，采用中国制造业采购经理指数中的从业人员指数（Employ）来反映就业状况。

2.4 数据来源

研究选取2015年1月到2020年5月的数据，选取16家上市银行的股票收盘价格，对股票价格的收益率进行对数化，选取沪深300的银行业指数作为银行业系统性风险的替代变量，也进行对数收益化的处理。数据来源于国泰安和wind数据库。在分析的过程中，将2015年1月到2019年12月的数据定义为疫情发生前，将2020年1月到2020年5月的数据定义为疫情发生后的数据，以此分别考察疫情发生前后的货币政策与系统性风险之间的关系。相关变量的描述性统计量见表1。

表1 描述性统计

3 实证分析

3.1 系统性风险度量结果

利用ARMA-GARCH模型对股票收益率进行建模，并根据建模结果得到系统性风险的大小，为了讨论的便利，将系统性风险设为正值，即数值越大则表示系统性风险越大。图1给出了八家银行的系统性风险随时间变化的曲线图，从图中可以看到，2015年之后到疫情发生前，大部分单个银行对银行业系统性风险的贡献呈现平稳波动的趋势，但是自疫情发生后，大部分银行对银行业系统性风险的贡献出现上升的趋势，说明疫情发生后，银行业的系统性风险在不断的增加，各个银行自身面临的风险加剧了整个行业的风险，在此背景下需要运用货币政策来化解系统性风险。

表2 新冠疫情发生前后系统性风险对比

3.2 新冠疫情背景下的货币政策对银行业系统性风险的影响

在疫情发生前，为了适应经济发展的需要，央行也不断对货币政策进行调整，在这一时期央行实行的是稳健的货币政策。疫情发生滞后，中央银行根据疫情对经济的冲击，不断调整货币政策，如2020年5月中央银行发布了第一季度货币政策执行的报告，报告透露新冠疫情发生以来央行采取了降低基准利率，扩大再贴现规模等货币政策手段。为了考察新冠疫情背景下的货币政策与系统性风险之间的关系，利用面板数据进行分析，具体的模型形式如下：

由于M2的数值较大，对其取对数化处理，最终得到的结果，如表3所示。为了对比新冠疫情发生前后的不同，先去除虚拟变量进行回归，回归模型为模型1，加入虚拟变量的回归模型为模型2。

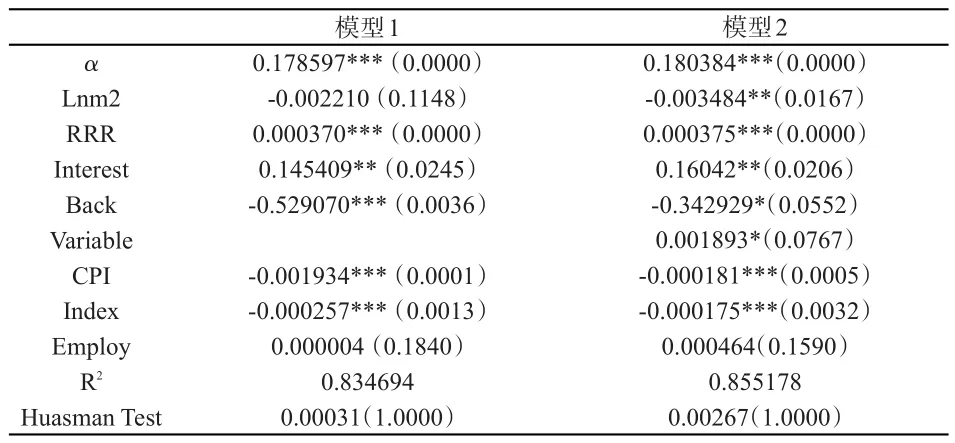
表3 模型回归结果

为了对模型1和模型2的面板回归模型进行选择，采用Hausman检验对固定效应和随机效应进行检验，从检验结果中可以看到，两个模型都应采用随机效应模型。

从表3的回归结果中可以看到，在模型1中，在10%的显著性水平下，除了流动性指标M2对系统性风险的影响不显著之外，其他的涉及到货币政策的变量都能对系统性风险有着显著的影响。在回归结果中可以看到，金融机构的存款准备金和基准利率对系统性风险是正向的影响，说明降低存款准备金和基准利率将会使得系统性风险降低，央行回购行为的原理是一致的，降低存款准备金也会释放一部分流动性，从而降低系统性风险，而降低基准利率，将减少银行的成本，从而改善银行的经营条件，降低风险。

在模型2中，当加入虚拟变量时，可以看到，在货币政策中的流动性指标M2在5%的显著性水平下对银行系统性风险有着显著的负向的影响，这相对于模型1的不显著来说，加入虚拟变量，提高了变量的解释能力。在两个模型的控制变量中除了就业人数变量不显著，其他变量均显著，说明了宏观经济变量也会对银行系统性风险产生影响，CPI和宏观经济景气指数都对银行系统性风险产生负向的影响，说明了宏观经济状况越好，越能降低银行系统性风险。同时从模型的整体效果中也可以看到，模型2的R2相较于模型1的R2有所提高，说明模型的解释能力有所增强，加入虚拟变量后模型的估计效果更好。

3.3 稳健性检验

从表4的结果中可以看到，剔除国有四大行后整体模型并没有发生显著的变化，模型中各个变量在10%的显著性水平下依然显著，同时整个模型的解释力也没有下降，反而在一定程度上模型的解释力有所上升，因此可以说明模型整体上是稳健的，并不受银行类型不同的影响。稳健性结果与模型2的结果基本一致，但在具体的变量系数上可以看到，核心变量中的流动性指标M2，存款准备金和基准利率对银行系统性风险的影响有所加强，说明这些指标对于其他银行的影响更大，更应值得关注。

4 结论及政策建议

基于新冠疫情发生前后的相关数据分析，得出以下结论：（1）疫情的发生增大了银行业的系统性风险；（2）货币政策对减低银行业系统性风险有着较为显著的作用。应对银行业系统性风险还可以从下几个方面入手：一是继续加强市场的流动性，货币政策的最主要的作用就是释放市场的流动性，保障银行在应对风险冲击时有足够的流动性；二是要发挥各种货币政策的作用，运用多种手段应对系统性风险；三是保障宏观经济的平稳运行。